导气式自动武器变质量热力学计算模型研究
2011-02-21冉景禄徐诚赵彦峻
冉景禄,徐诚,赵彦峻
(南京理工大学 机械工程学院,江苏 南京210094)
导气式自动武器是指利用从枪管导气孔流出的高温高压火药燃气推动自动机完成自动动作的武器,火药气体的恰当利用是自动武器良好动力学性能的基础[1]。因此,研究导气装置的动力特性对于利用火药燃气和获得自动武器良好的动力学特性都具有十分重要的意义。国外研究导气式自动武器的动力学特性时,大多采用的布拉文经验法、马蒙托夫经验法、布拉贡拉沃夫方法。国内的研究工作主要集中在2 个方面: 1)引进国外经验模型[2],并在此基础上建立导气装置数值计算模型[2-3]。数值计算模型求解的参数较多,计算相对准确,经验模型可求解的参数较少,误差相对较大。2)模型的改进与应用,这些研究针对特定对象对文献[1 -3]建立的计算模型进行部分改进,将其应用于侧装药金属风暴武器系统内弹道性能一致性问题[4]、导气装置优化设计问题[5-6]。但通观所有参考文献,可以发现:建立的数值计算模型和经验模型都没有考虑内弹道与导气装置耦合的变质量热力学过程,而且模型存在方程多、参数多、误差较大等不足; 所有的应用研究针对不同的研究对象改进模型时,也没有将内弹道和导气装置通过火药燃气耦合起来考虑。所以,为了克服这些研究的不足,探索导气式自动武器性能准确预测和结构参数的确定的方法,通过分析枪管和导气装置之间存在的变质量热力学过程,建立了一个内弹道和导气装置耦合的导气式自动武器变质量热力学计算模型,该模型更客观真实地描述了导气式自动武器发射过程中的变质量热力学过程,而且具有参数少、误差小等优点,实例证明了该模型的正确性和可靠性。
1 导气式自动武器变质量热力学模型
1.1 物理过程及基本假设
导气式自动武器的导气装置典型结构如图1所示。当底火被击锤撞击后,发射药开始燃烧,药室压力迅速增大,当弹丸底部压力大于挤进压力时,弹丸开始切入膛线加速运动。随着火药的燃烧和弹后空间不断增大,弹丸底部的压力逐渐减小,当弹丸位移大于导气孔的开孔距离时,火药燃气自导气孔流入导气室,由于刚开始膛内压力比导气室压力大很多,导气孔处出现正向临界(音速)流,随着流入导气室火药燃气的增多,导气室压力不断增大,导气孔处出现非临界(音速)流。随着弹丸继续向前运动、活塞向后运动,当导气室火药燃气作用于活塞断面的力与复进簧的簧力相等时,活塞运动速度达到最大,这时膛内压力会进一步减小,当膛内压力小于导气室压力且其比值不超过某一特定值时,导气室的高温高压气体开始流入膛内,导气孔处出现反向非临界(音速)流,当膛内压力与导气室压力的比值超过某一特定值时,导气孔处出现反向临界(音速)流。当弹头后端面飞离枪口时,弹丸运动进入后效期,高温高压的火药燃气以极高的速度喷出,由于火药燃气的流速极快,压力较大,弹丸仍然在受到火药燃气压力的情况下加速运动,随着弹丸位移的增加,火药燃气速度逐渐减缓,压力逐渐减小,后效期结束,弹丸速度达到最大。
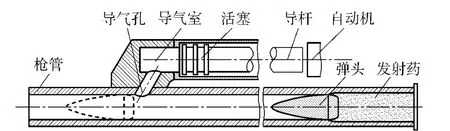
图1 导气装置结构示意图Fig.1 Sketch of gas-operated device
基本假设:
1)内弹道过程采用修正的经典内弹道模型描述;
2)导气装置内流场是一个有流入与流出的变质量热力学过程;
3)由于是瞬态计算,忽略火药燃气与枪管和导气室之间的热量交换;
4)内弹道与导气装置通过火药燃气流量相互耦合。
1.2 计算模型
导气式自动武器变质量热力学计算模型包括内弹道模型、导气室模型和耦合方程,具体形式如下:
膛内压力变化方程
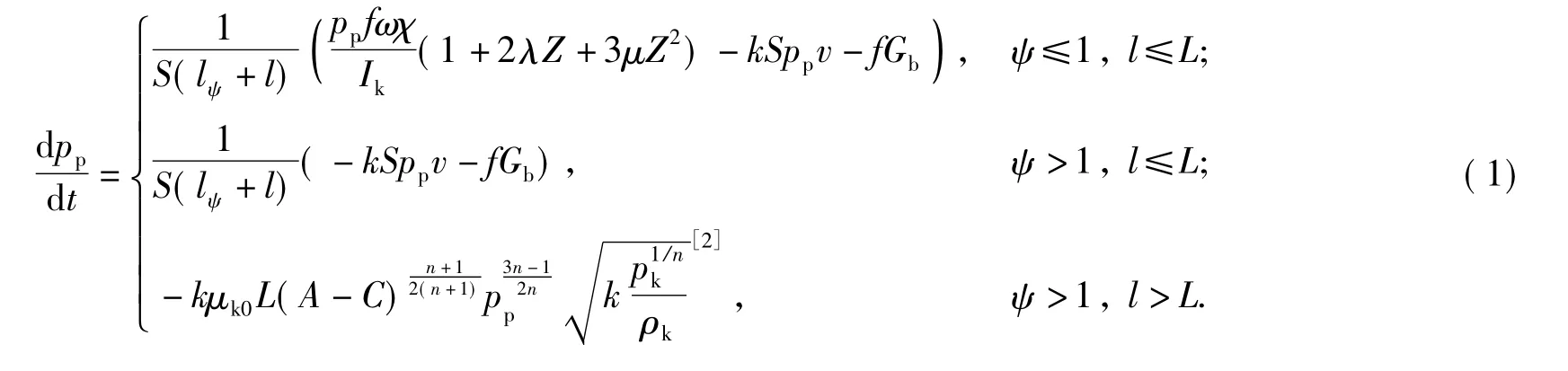
式中:pp、S、lψ、l、f、ω、Ik、Z、k、v、Gb、μk0、pk、ρk、L、n、ψ分别为导气室压力、枪管截面积、药室长度、弹头运动位移、火药力、装药量、火药燃气的压力全冲量、火药已燃相对厚度、绝热指数、弹头运动速度、导气孔处火药燃气的流量、枪口流量系数、枪口燃气压力、枪口燃气密度、枪管长、多变指数、火药已燃百分数。A、C 是与多变指数有关的常数。χ、λ、μ 为火药的形状特征量。
正比燃烧速度方程[7]

几何燃烧定律方程[7]
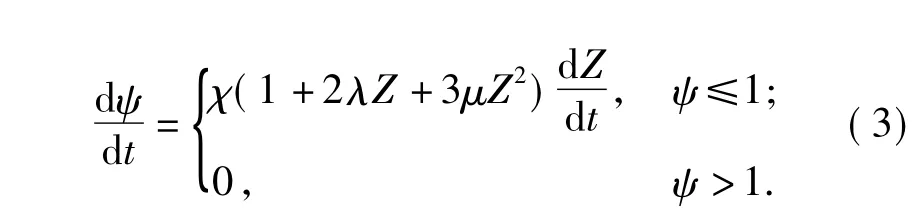
弹头运动位移方程[7]

弹头运动速度方程[7]

式中:φ 为次要功系数; m 为弹丸质量。
从导气孔流出枪管气体质量方程

式中:η 为流出枪管气体质量。
药室自由容积缩径表达式[7]
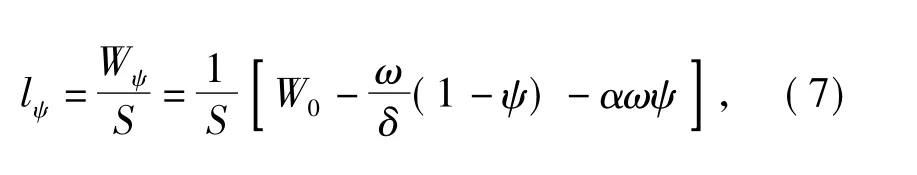
式中: W0为药室初始容积; δ 为火药密度; α 为余容。
枪管内火药燃气密度方程
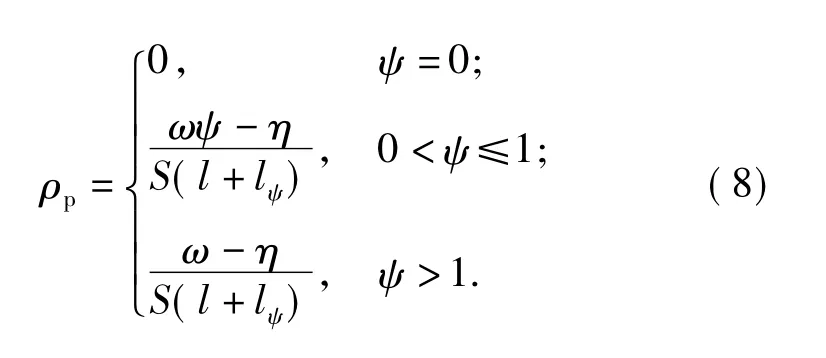
式中:ρp为枪管内火药燃气密度。
气室内气体压力变化方程[2]
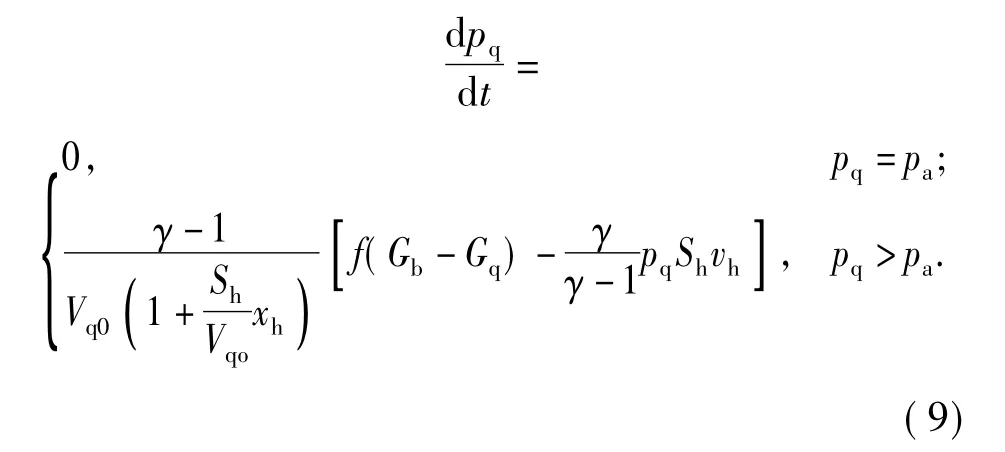
式中:pq、γ、Vq、Vq0、Sh、vh、pa分别为导气室压力、比热比、导气室容积、导气室初始容积、活塞横断面面积、活塞运动速度、大气压强。
活塞间隙的流量方程[2]
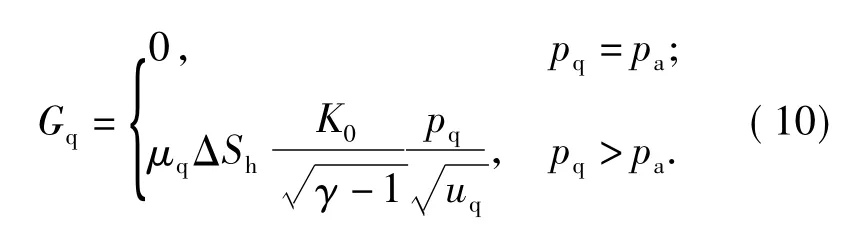
式中:Gq、ΔSh、μq、γ、uq分别为活塞间隙气体流量、导气活塞的间隙面积、导气室的流量系数、比热比、气体单位质量内能,K0为与γ 有关的常数。
气室内气体质量变化速度方程[2]

式中:mq为导气室内火药燃气质量。
活塞运动方程
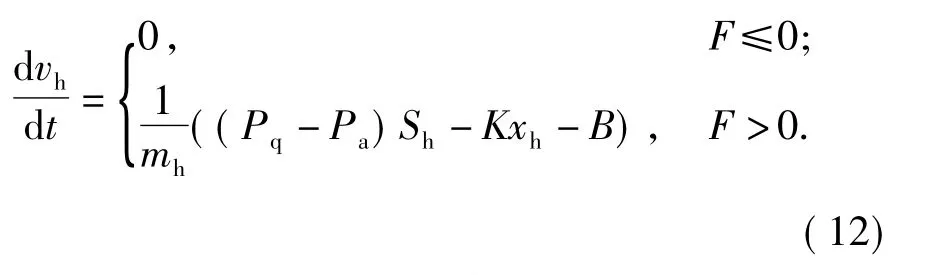
式中:K、xh、B、mh分别为缓冲簧刚度、活塞位移、随动机构摩擦力和传动阻力、活塞质量;F=(Pq-Pa)·Sh-Kxh-B 为活塞所受到的合力。
活塞运动位移方程[2]

气室内气流质量守恒方程
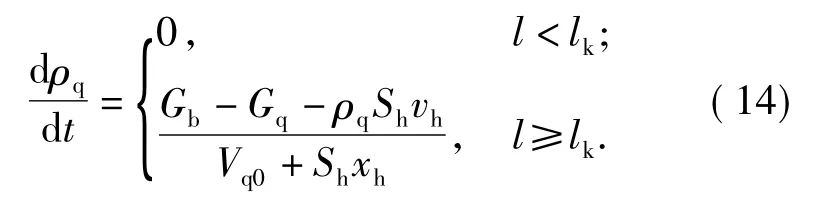
式中:ρq、lk分别为气室内气体密度和开孔距离。
气室内单位质量气体的比内能方程[2]
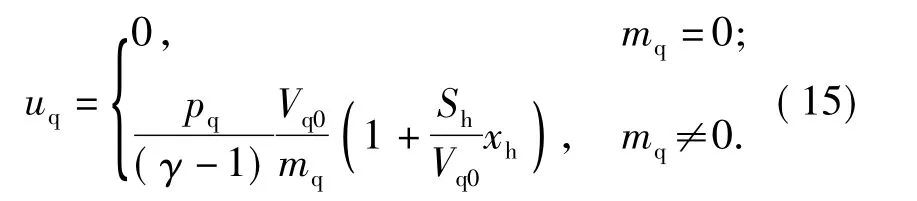
耦合(导气孔流量)方程[1-2]
枪管内的内弹道过程与导气装置通过流量方程耦合在一起。
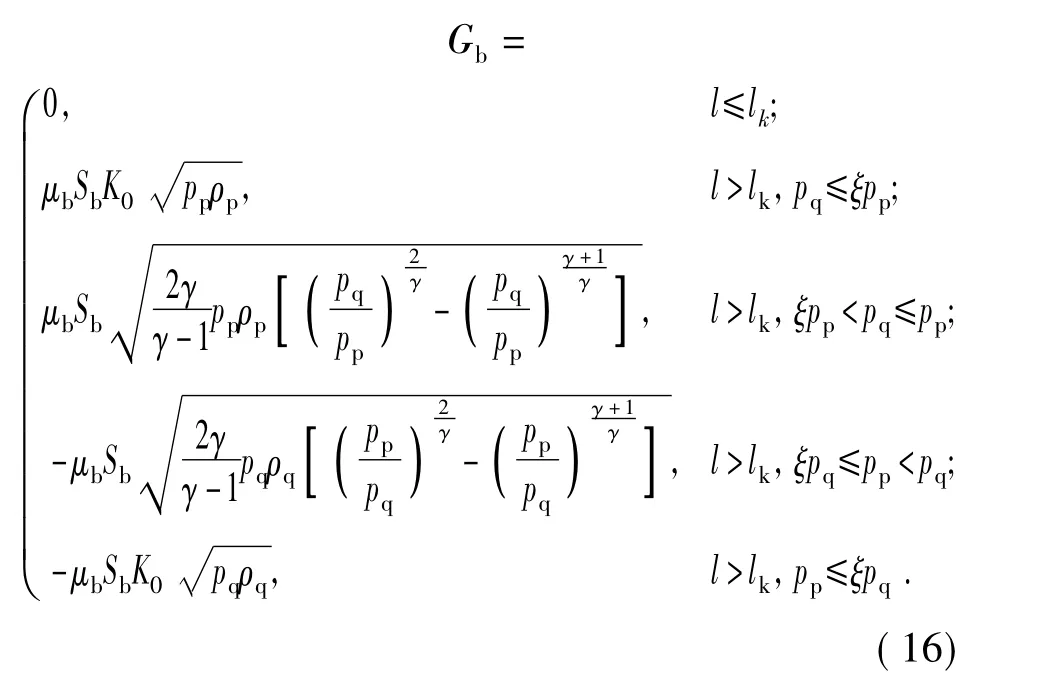
式中:μb、Sb分别为导气孔处流量系数、导气孔开孔面积;
2 模型验证及计算结果分析
2.1 模型验证
图2为实验获得的某自动武器自动机速度时间图,为了验证所建模型的正确性,利用模型对某自动武器的各动力学参数进行数值计算。利用四阶龙格库塔法进行模型求解,采用MATLAB 编程实现。通过理论计算,得到某自动武器自动机的后坐初始阶段速度时间图,将其与实验获得的速度时间图的后坐初始阶段的曲线进行对比,如图3所示。可以看出,由于没有考虑发射时后坐力通过弹底对自动机速度的影响,理论计算时该段速度为0.当导气室内火药燃气推动导气活塞使自动机向后运动时,理论计算的速度曲线与实验获得的速度曲线吻合比较好,后坐的最大速度基本一致。从而表明本文建立的导气式自动武器变质量热力学计算模型是正确可靠的。
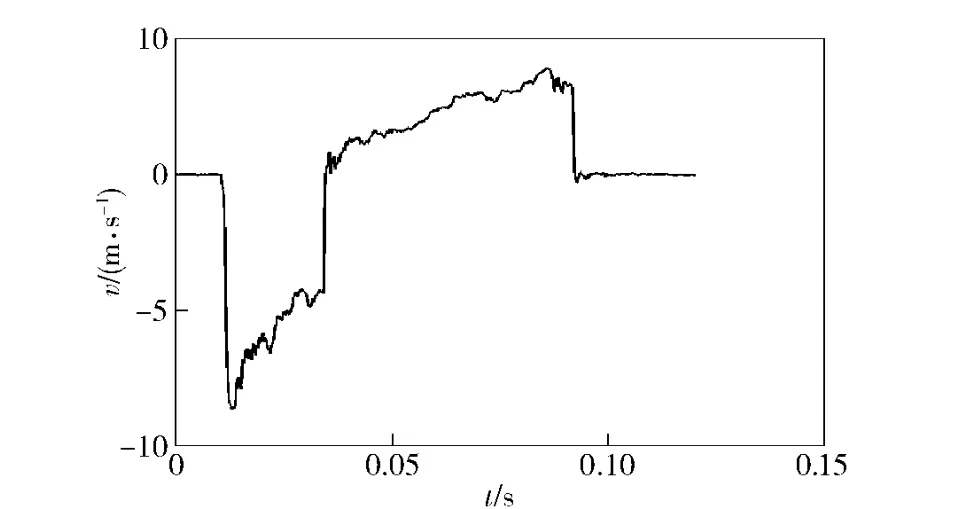
图2 自动机速度时间图Fig.2 v-t graph of automatic mechanism
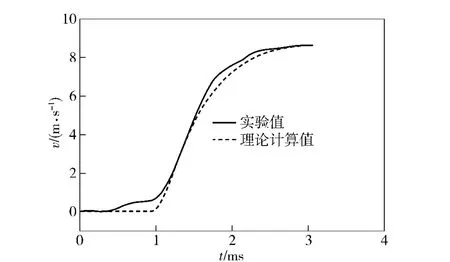
图3 后坐初始阶段速度对比图Fig.3 v-t at recoiled phase
2.2 计算结果分析
2.2.1 导气孔处流量分析
某导气式自动武器导气孔处流量如图4所示,当弹丸到达导气孔时,膛内压力很大,而导气室内压力仅为一个大气压,从而在导气孔处出现正向临界流,流量在瞬间达到1.16 kg/s;随后流量开始下降,当弹丸飞离枪口,火药燃气快速喷出,膛内压力迅速下降,导气孔处燃气出现正向非临界流;当弹丸继续向前运动,膛内压力进一步下降,当导气室压力大于膛内压力,导气孔处出现反向非临界流,最大反向非临界流流量为0.18 kg/s;随着导气室内燃气不断流入膛内,导气室压力逐渐下降,流量随之减小,直至为0.
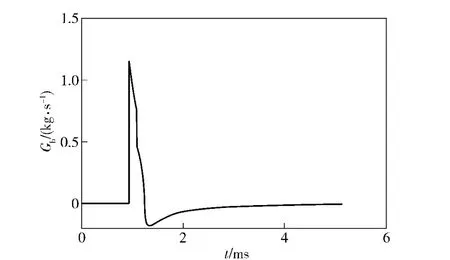
图4 气体流量图Fig.4 Gas flux
2.2.2 耦合量对膛压、初速的影响
比较有无考虑耦合能量的膛内压力曲线(如图5所示)可以看出,在弹丸运行至导气孔处到后效期段,膛内压力曲线在开始和末端差别较小,而中间压力之差相对较大的特点。其中,当弹丸刚飞离枪口端面时压力之差达到最大的6.7 MPa.图6为有无考虑耦合能量时弹丸的速度曲线,可以看出,火药燃气的耦合能量对弹丸飞行速度影响也较为明显,对出膛速度的影响大约为6 m/s,在后效期的终了段,对速度的影响可达到最大的16 m/s.从而表明: 导气孔流入导气室的火药燃气对膛内压力和弹丸初速有一定的影响,所以在内弹道求解和导气装置动力学求解时,应考虑从导气孔流出的耦合能量对膛内压力和初速的影响。
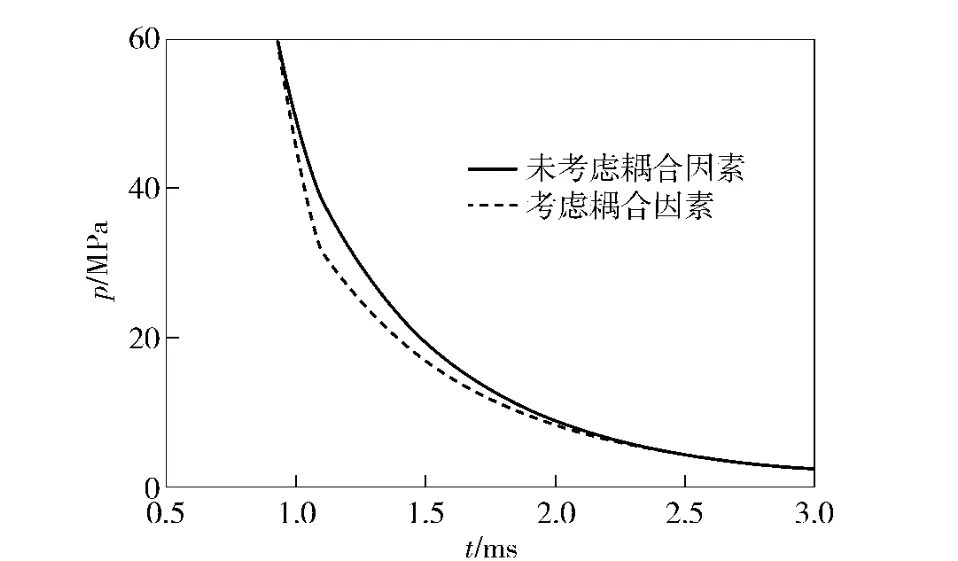
图5 耦合能量对膛压影响图Fig.5 Impact of coupling energy on bore pressure
2.2.3 初始容积对导气装置影响
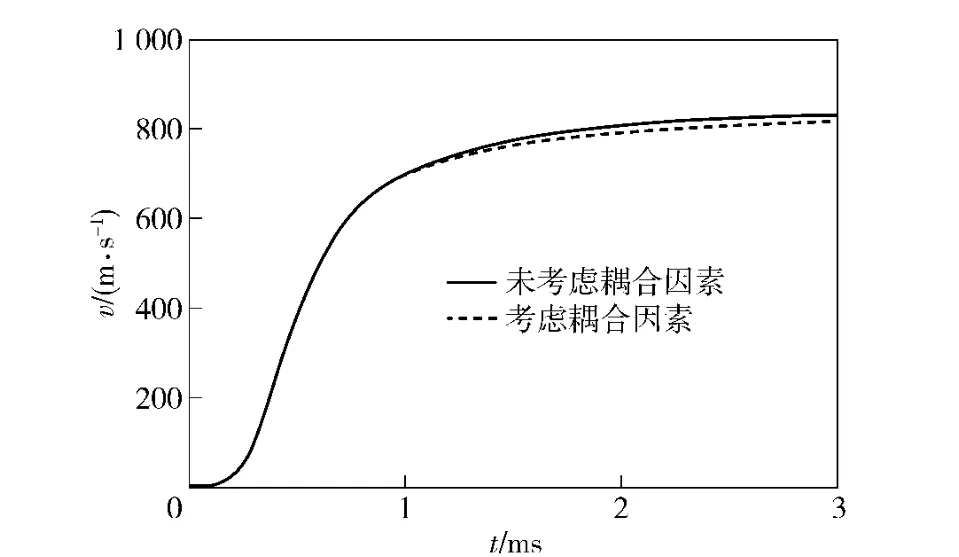
图6 耦合能量对弹丸速度影响图Fig.6 Impact of coupling energy on bullet speed
不同初始容积对导气室压力和自动机最大后坐速度的影响,如图7、图8所示。某自动武器导气室的初始容积为1.7 ×10-6m3,此时,理论计算导气室的最大压力为23.7 MPa,自动机的后坐最大速度为8.61 m/s;当初始容积分别为2.2 ×10-6m3、2.7 ×10-6m3时,导气室最大压力分别为21.4、19.7 MPa,自动机的后坐最大速度分别为8.38、8.24 m/s.由此可以看出,随着初始容积增大,导气室压力会减小,而且压力峰值出现时间会后移,自动机后坐最大速度会减小,而且,随着初始容积的增加,压力减小的加速度会降低。这说明初始容积对导气室的压力、最大压力出现的时间和自动机后坐的最大速度都有影响。换言之,在进行导气装置设计时可以通过调节导气室的初始容积来调整导气室内气体的压力及其出现的时间和自动机后坐的速度。
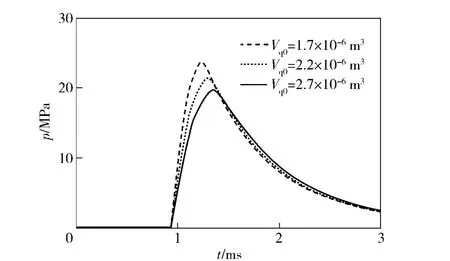
图7 初始容积对导气室压力影响图Fig.7 Impact of initial volume on gas chamber pressure
2.2.4 间隙对导气装置影响
不同间隙对导气室压力和自动机后坐速度的影响,如图9、图10所示。某自动武器导气活塞与导气筒的间隙为0.1 mm,此时,导气室的最大压力为23.7 MPa,自动机后坐最大速度8.61 m/s;当导气活塞与导气筒的间隙分别为0.5、1 mm 时,导气室最大压力分别为23.2、21.4 MPa,自动机后坐最大速度分别为8.48、8.18 m/s;这说明间隙在0.5 mm 以下变化,对导气室压力和自动机后坐最大速度影响不大。但当间隙增大到1 mm 时,导气室的压力较之0.5 mm 时减小了1.8 MPa,自动机后坐最大速度减小了0.3 m/s.说明间隙在0.5~1 mm 之间变化时,导气室压力和自动机后坐最大速度变化较为明显。但压力峰值到来的时间基本保持不变,这说明进行导气装置设计时导气活塞与导气筒的间隙控制在0.1~0.5 mm 之间比较合适。
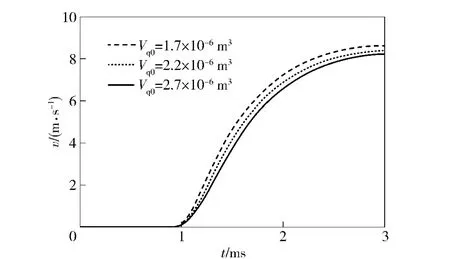
图8 初始容积对自动机速度影响图Fig.8 Impact of initial volume on automatic mechanism speed
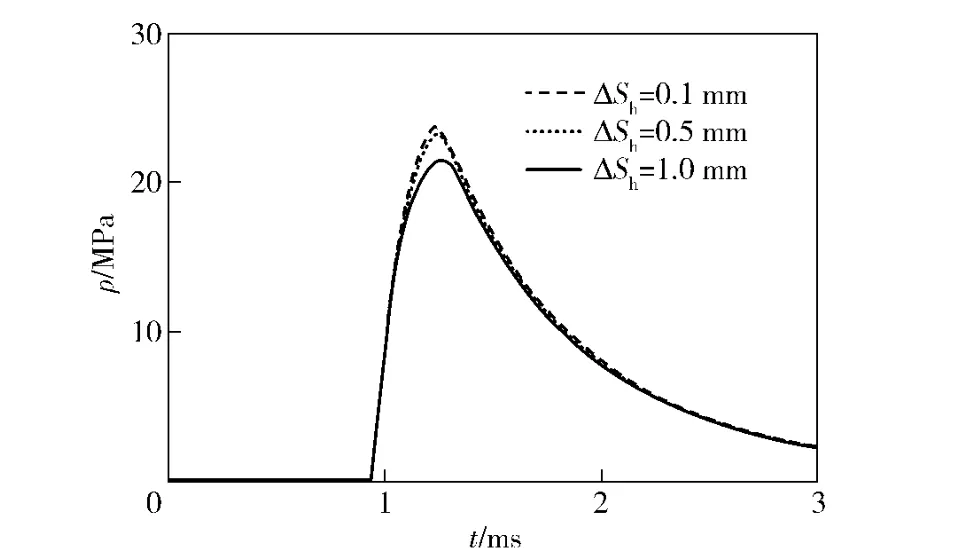
图9 间隙对导气室压力影响图Fig.9 Impact of clearance on gas chamber pressure
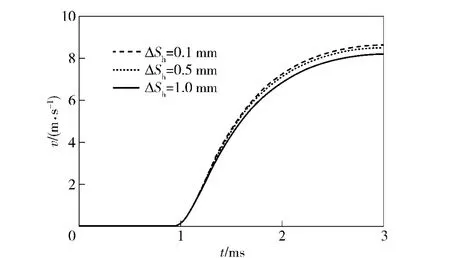
图10 间隙对自动机速度影响图Fig.10 Impact of clearance on automatic mechanism speed
2.2.5 导气孔直径对导气装置影响
不同导气孔直径对导气室压力和自动机后坐速度的影响,如图11、图12所示。随着导气孔直径增大,导气室压力会随之增大,自动机后坐速度也会随之增大。而且开孔直径在越小的值附近变化时,导气室压力和自动机最大后坐速度的变化越敏感。
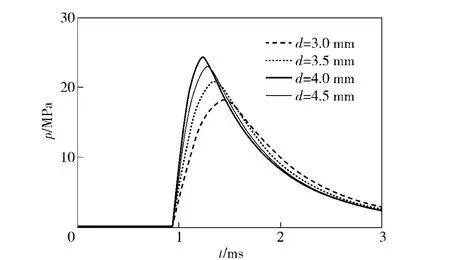
图11 导气孔对导气室压力影响图Fig.11 Impact of clearance on gas chamber pressure
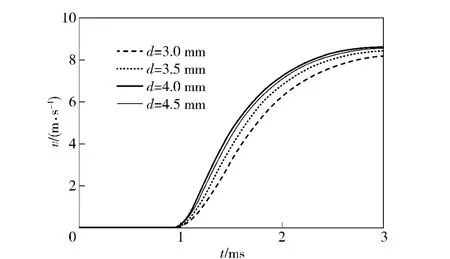
图12 导气孔对自动机速度影响图Fig.12 Impact of clearance on automatic mechanism speed
3 结论
1)通过分析导气式自动武器发射过程中身(枪)管和导气装置之间存在的变质量热力学过程,建立了一个包括内弹道与导气装置耦合的一体化变质量热力学模型,并以自动武器为实例验证了该模型的正确性。
2)利用该模型求解了考虑耦合能量和不考虑耦合能量情况下,膛内压力和弹头速度的变化趋势,得出耦合能量对两者有一定影响,在进行内弹道和导气室动力学特性精确求解时应该考虑该因素的结论。
3)本文建立的模型可以定量求解导气装置不同结构参数对导气室压力和自动机速度的变化,可用于探讨各参数变化对导气室压力和自动机速度的影响规律。
4)本文建立的模型可以定量分析导气式自动武器导气孔处气体流量变化,得出气孔处气体流量的基本变化规律。
References)
[1]甘高才.自动武器动力学[M].北京: 兵器工业出版社,1990:26 -33.GAN Gao-cai.Dynamics of automatic weapon[M].Beijing: The Publishing House of Ordnance Industry,1990: 26-33.(in Chinese)
[2]陆家鹏.自动武器学气体动力学分册[M].北京: 国防工业出版社,1988:456 -464.LU Jia-peng.Gas dynamics of automatic weapon[M].Beijing:The Publishing House of Ordnance Industry,1988:456 -464.(in Chinese)
[3]廖振强,王涛,余世海.武器气体动力学数值计算方法[M].北京:国防工业出版社,1988:221 -228 LIAO Zhen-qiang,WANG Tao,YUE Shi-hai.The calculation method of gas dynamics of weapon[M].Beijing: The Publishing House of Ordnance Industry,1988:221 -228.(in Chinese)
[4]倪志军,周克栋,赫雷.侧装药金属风暴武器系统内弹道性能一致性研究[J].兵工学报,2005,26(5):595 -599.NI Zhi-jun,ZHOU Ke-dong,HE Lei.Consistency research of interior ballistic performances of the metal storm weapon system with side powder chambers[J].Acta Armamentarii,2005,26(5):595-599.(in Chinese)
[5]韩晓明,薄玉成,王惠源,等.内能源转管武器导气装置结构参数优化设计[J].火炮发射与控制学报,2008,(2): 50 -53.HAN Xiao-ming,BO Yu-cheng,WANG Hui-yuan,et al.Optimal design of gas-operated device structure parameter in internallypowered gatling weapon system[J].Journal of Gun Launch &Control,2008,(2): 50 -53.(in Chinese)
[6]王万清.M60 式7.62 mm 通用机枪动力学分析及优化[D].南京:南京理工大学,2007:21 -24.WANG Wan-qing.Analysis on dynamics and optimization of model M60 general purpose machine gun of the 7.62 mm caliber[D].Nanjing: Nanjing University of Science and Technology,2007:21-24.(in Chinese)
[7]步兵自动武器及弹药设计手册编写组.弹道及弹药射击: (上册)[M].北京:国防工业出版社,1977:39 -84.Compile Group of Infantry Automatic Weapon and Design of Ammunition.Manual of infantry automatic weapon and design of ammunition[M].Beijing: National Defense Industry Press,1977:39-84.(in Chinese)
