基于惯性测量的输电导线覆冰运动特征提取
2019-04-22杨金显晁丽君李双磊
杨金显, 晁丽君, 李双磊
(1. 河南理工大学 电气工程与自动化学院,河南 焦作 454003;2.国网山东临朐供电公司,山东 临朐 262600)
由于不同气候条件影响,输电导线会出现不同的运动状态,从振幅和频率看,主要为高频微幅的微风振动,中频中幅的次档距振荡和低频大振幅的覆冰运动。其中,覆冰运动是对输电线路危害最大的一种运动。覆冰运动公知的幅值范围约为导线直径的5倍~300倍、频率范围约为0.1~3 Hz。总的来说输电导线覆冰运动包括平动(水平和垂直运动统称为平动)和扭动等,覆冰初期导线在平衡位置附近做微幅振动,随着覆冰程度增大和风激励的影响,水平振动向垂直振动转变,并逐渐趋于稳定。当幅值和扭动达到一定程度时,形成以垂直方向运动为主的低频大振幅舞动,舞动使导线弧垂度增大、轴向应力增加,疲劳极限降低,极易造成导线断股;同时会使绝缘子串、横担及杆塔荷载变大,造成绝缘子摆动、横担变形、杆塔倾斜等严重灾害,对电网安全运行构成极大威胁,对国民经济造成直接损失[1]。因此导线运动阻尼器的设计和安装就变得尤为重要,但对于某个具体地区来说,导线运动存在主要的幅值和频率,要想针对性设计出适合某地区的运动阻尼器就需要识别出某地区导线的具体运动特征信息,进而根据运动特征信息设计阻尼器参数。为有效预警和阻尼某地区覆冰运动,采集输电导线三轴加速度(平动)和三轴角速度(扭动)运动信息,经过预处理后计算多维时间序列的相关系数矩阵,对相关系数矩阵进行奇异值分解提取运动特征,然后通过相关分析法估计导线运动的幅值和频率,从而为阻尼器的设计提供理论参数。
近年来,由于MEMS传感器体积小、功耗低、成本低、抗振性能好和可靠性高等优点,已有学者采用MEMS传感器对输电线路运动进行监测研究[2]。Wang等[3-4]采用MEMS加速度计多点监测导线振动加速度,根据异常加速度信息检测舞动并进行等级划分;邵颖彪等[5]提出采用九轴传感器测量导线舞动的扭转和平动,用来克服只用加速度计监测导线舞动只能得到位移信息的缺陷;Huang等[6-7]考虑导线自激振荡和导线扭转引起的导线舞动,设计了一种舞动惯性测量单元,避免导线舞动时计算的相对位移与导线扭转引起的实际位移的偏差;汪滔等[8]提出一种改进的MEMS陀螺仪和加速度计互补滤波算法,设计了舞动轨迹的解算方法,对陀螺计算出的角度进行误差修正。在上述装置和方法中:加速度计会随导线发生扭转,对通过积分计算得到的输电线运动轨迹等参数会造成计算不准,尽管惯性传感器能够克服单独使用加速度传感器带来的那些问题,但实现这种功能需要导航级的惯性测量系统,体积大且成本昂贵,况且姿态解算需要精确的初始值,而且产生的累计误差;另外采用单一特征对导线运动分析,会割裂数据整体的内在联系,无法准确识别输电导线的整体运动特征。
在以上研究的基础上,提出一种MIMS多维时间序列覆冰运动特征提取方法:通过MEMS惯性测量系统测量导线运动加速度和角速度等信息,不通过姿态解算,而是直接利用原始信息进行处理,对多维时间序列的相关矩阵进行奇异值分解,构建加权特征矩阵作为输电导线整体运动特征,然后采用近邻分类法进行覆冰舞动识别。同样,该算法也适用于其它导线运动形式检测,当待识别的加权特征矩阵与输电导线其他运动形式时的加权特征矩阵相似度较高时,可判定导线以该形式运动。本文所提方法降低了数据的维数,提高了处理速度和运动特征识别精度。
1 MIMS数据采集与处理
1.1 信号采集与预处理
由于导线附近具有较强的电磁干扰,MEMS惯性测量系统不能直接安装于导线上,为此采用一定长度的防磁中空弹性杆,一端固定于绝缘子串悬挂点,另一端安装MEMS惯性测量节点,来测量导线运动的三轴加速度和三轴角速度等信息。弹性杆内放置电源线、地线和数据线,并且数据线封装于屏蔽层内,采用电流互感器整流变压后直接给测量节点供电,为避免信号受到干扰,把采集的数据通过电力光缆传输给监控中心进行数据处理[9]。
目前对于输电导线运动的测量主要是对单一特征的识别,但是由于MIMS各轴加速度和角速度之间存在着内在耦合关系,单一轴向的加速度或角速度无法表征整个输电导线的运动特征,而多维时间序列既可以描述某一时刻导线三个轴向的转动运动信息,又包含了不同时刻导线平动以及这些运动的相互关系。为了准确识别覆冰运动,考虑外部因素影响及导线运动的整体关系,将三轴加速度和三轴角速度信号由6维时间序列表示:
X={ax,ay,az,ωx,ωy,ωz}
(1)
式中:ax,ay,az为三轴加速度序列,ωx,ωy,ωz为三轴角速度序列,将上式记为X={x1,x2,…,xi,…,x6},xi={ai1,ai2,…,aiN}T,N为序列长度。
MEMS惯性传感器在工作过程中有周期漂移项的存在,会对运动分析结果造成影响;另外随机干扰信号也是系统主要误差源之一,传感器在工作中极易产生低频周期性信号[10]。由于这些周期趋势项的存在,通过二次积分所得的运动位移轨迹可能有较大程度的偏离实际,甚至产生畸变或失真,因此需要消除趋势项和随机噪声,需采取合适的方法减少信号中的干扰成分。常用的去噪方法有小波去噪和Kalman去噪,虽然这两种方法都能在一定程度上平滑MEMS信号,但采用小波去噪方法阈值选取比较困难,且依赖于信号噪声统计特性;基于Kalman滤波的去噪方法,只适用于噪声特性易知的场合,然而由于外界环境影响,MEMS信号噪声较为复杂,且具有时变性,动态系统模型的状态噪声和观测噪声统计特性往往具有不确定性。因此上述依赖噪声统计特性的方法,在输电导线运动信号处理中很难获得理想的去噪效果。由于五点三次平滑法可减小时域信号中的随机噪声,有效处理周期性的干扰信号或不规则的随机干扰信号所引起的尖峰、毛刺现象,适用于输电导线运动的MEMS信号去噪场合,且计算简单方便,因此本文采用五点三次平滑法对数据进行滤波处理,其计算公式为:
(2)
1.2 信号处理效果评价
为了描述输电导线在不同时刻的运动加速度和角速度的变化关系及其变化趋势,建立一多维时间序列X的矩阵模型,以便于后续运动特征提取。为消除偶然测量误差,采用移动滑窗的方法对数据进行分段,将长度为L的时间窗在多维时间序列上滑动并取平均。对处理过的多维时间序列建立时变测量矩阵Xn×6,其中,n=N/L。
(3)
信号预处理后,通过信噪比来验证信号处理效果。信噪比是测量信号中的噪声量的传统方法,常被用作去噪效果评价指标。信噪比定义如下,单位为dB:
SNR=10ln(Ps/Pn)
(4)
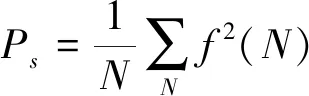
NRR=1/(SNR+1)+ε
(5)
式中:NRR为噪声剩余率,ε为误差因子。当NRR∈(0,0.1)时,说明剩余噪声量较少,去噪效果较好;当NRR∈(0.1,0.3)时,说明剩余噪声量较多,去噪效果一般;当NRR∈(0.3,1)时说明剩余大量噪声,去噪效果不好。
由于加速度和角速度量纲和运动特征方面具有差异,根据max-min法将导线运动三轴加速度和三轴角速度的值归一化得到新的各维的序列值:
(6)
式中:xi max和xi min分别为各维加速度或角速度测量序列的最大值和最小值。
2 运动特征提取与识别
2.1 信号特征提取
尽管输电覆冰线路运动形式复杂,幅度和频率都在变化,但其基本运动模式为平动和扭动。导线平动时,X、Y和Z轴加速度、角速度信号与各自轴向相似程度较高,自相关系数较大;当导线的扭转频率与其横向运动频率相接近时,覆冰导线产生偏心惯性,诱使导线发生扭动,X轴加速度和角速度向Y轴或Z轴转化,三轴发生交叉耦合运动,X、Y和Z轴信号与其他轴向相似程度较高,互相关系数较大。
导线运动多维时间序列观测值数目不同时,无法采用传统的欧氏距离进行相似度分析,为了体现MIMS各轴加速度和角速度之间的相互关系,同时解决MEMS测量数目不同的问题,计算运动矩阵X′的相关系数矩阵RX′[11],对信号整体内在关系进行分析。
(7)
采用相关系数矩阵对输电导线运动进行分析,既可以表征导线运动的加速度和角速度相互关系,又将运动特征矩阵固定为6×6维,便于矩阵之间相似性度量。由于噪声干扰的存在,会对输电导线运动的识别结果造成影响,因此对导线运动的相关系数矩阵RX′进行奇异值分解提取导线的运动特征[12]。
RX′=UΛUT
(8)
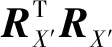
2.2 加权矩阵计算
奇异值可以反映出MIMS采集的信号中的有用信号和噪声的能量分布特点,在奇异值分解中,大的奇异值对应的特征向量包含了更多导线运动信息,具有较高的鉴别性,特征矩阵中能够表征MIMS信号特征的有用信号主要由前k个较大的奇异值反映出来,而后6-k个较小的奇异值对输电导线运动影响不大。较大的奇异值对应的奇异向量在矩阵特征识别中所占权重较大,而奇异值所占比例大小可以反映出特征向量所占权重。通过对特征矩阵进行加权,进行输电导线的运动特征识别[13]。采用归一化奇异值的方法计算加权矩阵:
(9)
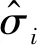
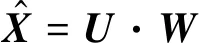
(10)
利用对多维时间序列的相关系数矩阵奇异值分解后的特征值构造加权特征矩阵,通过计算两个多维时间序列加权特征矩阵之间的相似度,识别导线运动形式,大大降低了计算量,并提高了运动形式识别精度。
2.3 覆冰运动识别
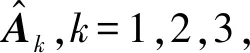
(11)
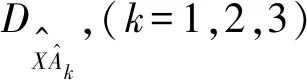
对于输电导线的覆冰运动特征识别,首先对MIMS采集的原始多维时间序列进行预处理并建立时变测量矩阵;然后计算相关系数矩阵并进行奇异值分解,根据特征向量和特征值计算加权特征矩阵,对导线运动特征进行提取;最后通过度量当前序列的加权特征矩阵和基准特征矩阵之间的相似性,采用近邻分类法识别覆冰运动,具体算法流程如图1所示。
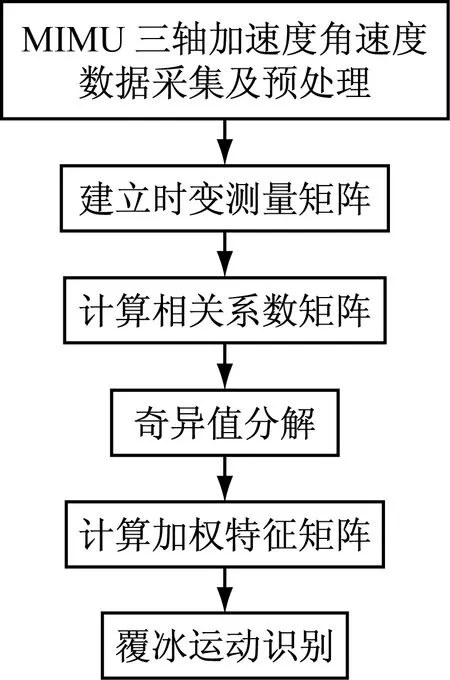
图1 覆冰运动识别算法流程Fig.1 Motion identification algorithm procedure of iced conductor
2.4 覆冰运动幅值和频率估计
由于输电网络覆冰运动的复杂性,拟合覆冰运动轨迹比较困难且容易出现解算误差。输电导线覆冰运动时,平动与扭动伴随而生,通过对加速度和角速度信号进行相关分析,进而估计覆冰导线幅值和频率变化程度。首先对MEMS信号平滑分段并归一化处理,将加速度和角速度特征量尺度变换到相同的范围,以便于统一计算。将输电线路静止或微风振动情况下的时变测量矩阵作为初始矩阵,初始矩阵第i时间段的信号记为xi,通过计算覆冰测量矩阵与初始矩阵在同一时间段的相关系数,度量MEMS信号的变异程度,进而根据相似程度预测覆冰导线幅值变化程度(相关系数越小,数据相似程度越低,幅值变化程度越大)。覆冰测量矩阵与初始矩阵第i时间段的相关系数Ra为:
(12)
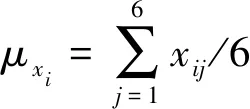
覆冰导线运动信号的变化频率即导线运动频率。通过计算覆冰测量矩阵当前时间段与上一时间段的相关系数,度量信号的变异速率,进而根据变异速率预测覆冰导线频率变化程度(相关系数越小,数据相似程度越低,频率变化程度越快)。相邻时间段信号的相关系数Rc为:
(13)
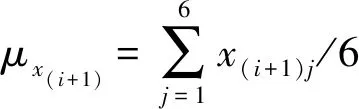
分别记d为幅值变异程度,f为频率变异速率,由于数据存在一定误差,考虑误差因素,则[15]:
d=(1-Ra)+ε1
(14)
f=(1-Rc)+ε2
(15)
式中:ε1、ε2为误差因子。
输电导线微风振动时为高频微幅运动,次档距振荡时为中频中幅运动,覆冰舞动时为低频大振幅运动。为进一步验证覆冰识别算法的有效性,按照上述算法估计导线在微风振动和次档距振荡运动状态下幅值和频率变异程度,并和覆冰运动进行比较。
3 实 验
为验证上述输电线路覆冰运动识别及幅频估计算法,按一定比例设计了输电线路模型,将MIMS按1.1节方案安装于模型,搭建如图2所示输电线路运动识别系统,采集输电导线在微风振动和次档距振荡时的数据作为基准数据并进行特征提取,通过监控主机或智能终端监测导线运动并保存数据。

图2 输电网络运动测试系统Fig.2 Motion test system of power transmission network
由于白蜡密度与冰相似,将导线拉直偏置于椭圆模具中,将白蜡融化注入模具覆在导线上,在白蜡上涂上一层胶,在硬度上也和冰保持一致,模拟偏心覆冰导线,采集MIMS信号作为覆冰基准数据并进行特征提取,模拟覆冰导线,如图3所示。
采集任意一组输电导线覆冰运动时的MEMS信号通过五点三次平滑法预处理,如图4所示。由图4可知,预处理后可有效减少随机噪声、尖峰和毛刺现象。
取L=30,将预处理数据滑动平均分段。为定量分析数据处理效果,根据式(4)和式(5)分别计算三轴加速度和三轴角速度信号的信噪比和噪声剩余率,噪声剩余率如表1所示。由表1可知,三轴加速度和三轴角速度的噪声剩余率都在(0,0.1)之间,说明去噪效果良好。

图3 模拟覆冰导线Fig.3 Analog iced conductor

表1 噪声剩余率Tab.1 Noise residual ratio
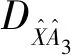

表2 运动特征矩阵与三种基准矩阵距离Tab.2 Distance between motion characteristic matrix and three reference matrices
采用相关分析法,对同一时间段覆冰测量矩阵与初始测量矩阵MEMS信号进行相关分析,估计覆冰导线幅值变异程度;对相邻时间段覆冰测量矩阵MEMS信号进行相关分析,估计频率变异速率。同时,估计导线微风振动和次档距振荡时的幅值和频率,并与覆冰运动进行比较,三种形式运动特征的幅值和频率变化分别如图6和图7所示。
由图6和图7可知,微风振动时导线近似做高频微幅运动,次档距振荡时导线近似做中频中幅运动,覆冰运动时导线近似做低频大振幅运动。不同运动状态下导线幅值频率曲线走势进一步说明了算法的有效性。根据所估计的幅值频率变化,可以获取本地区覆冰输电导线运动特性,为后续振动阻尼器设计提供参数。

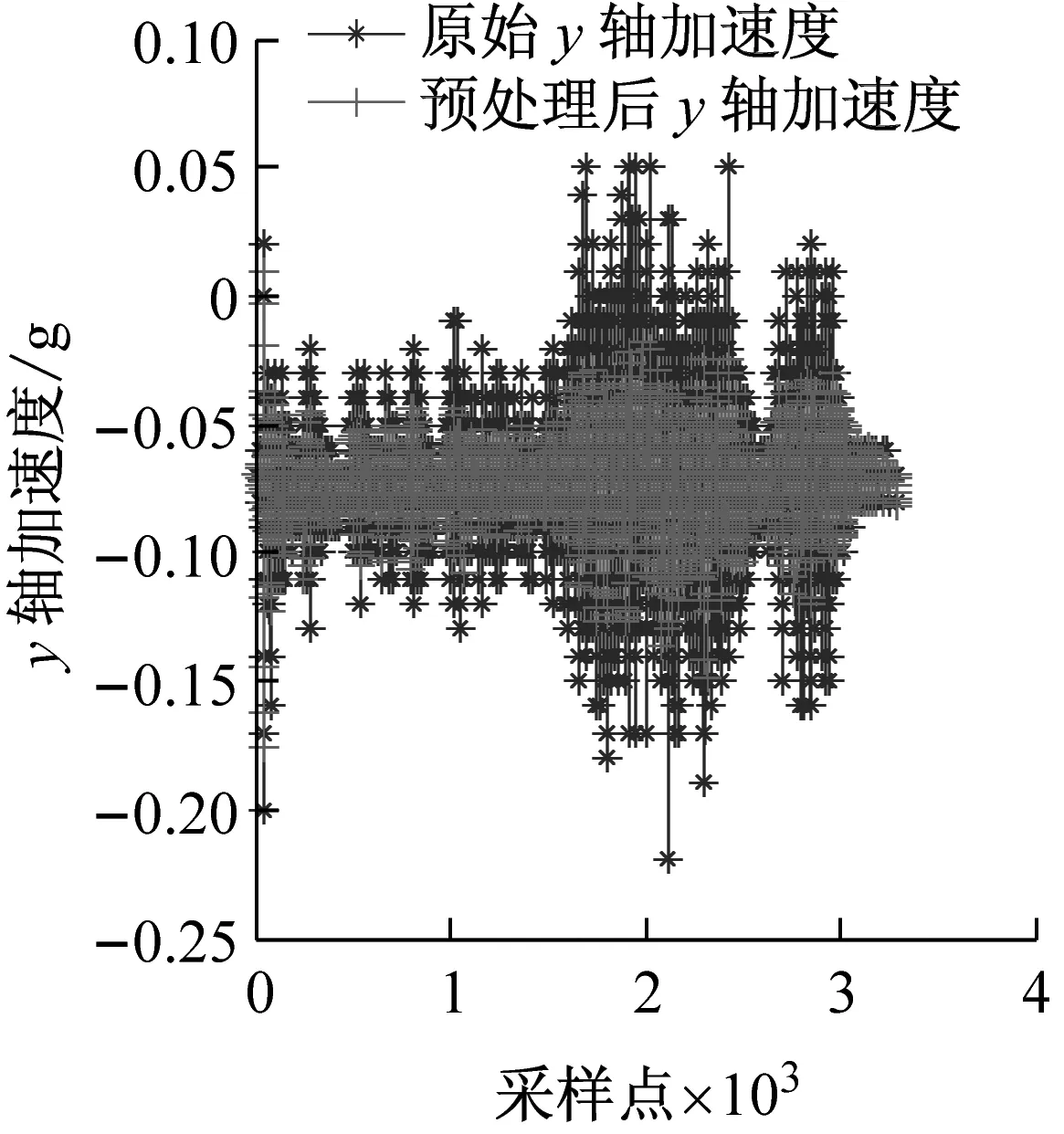
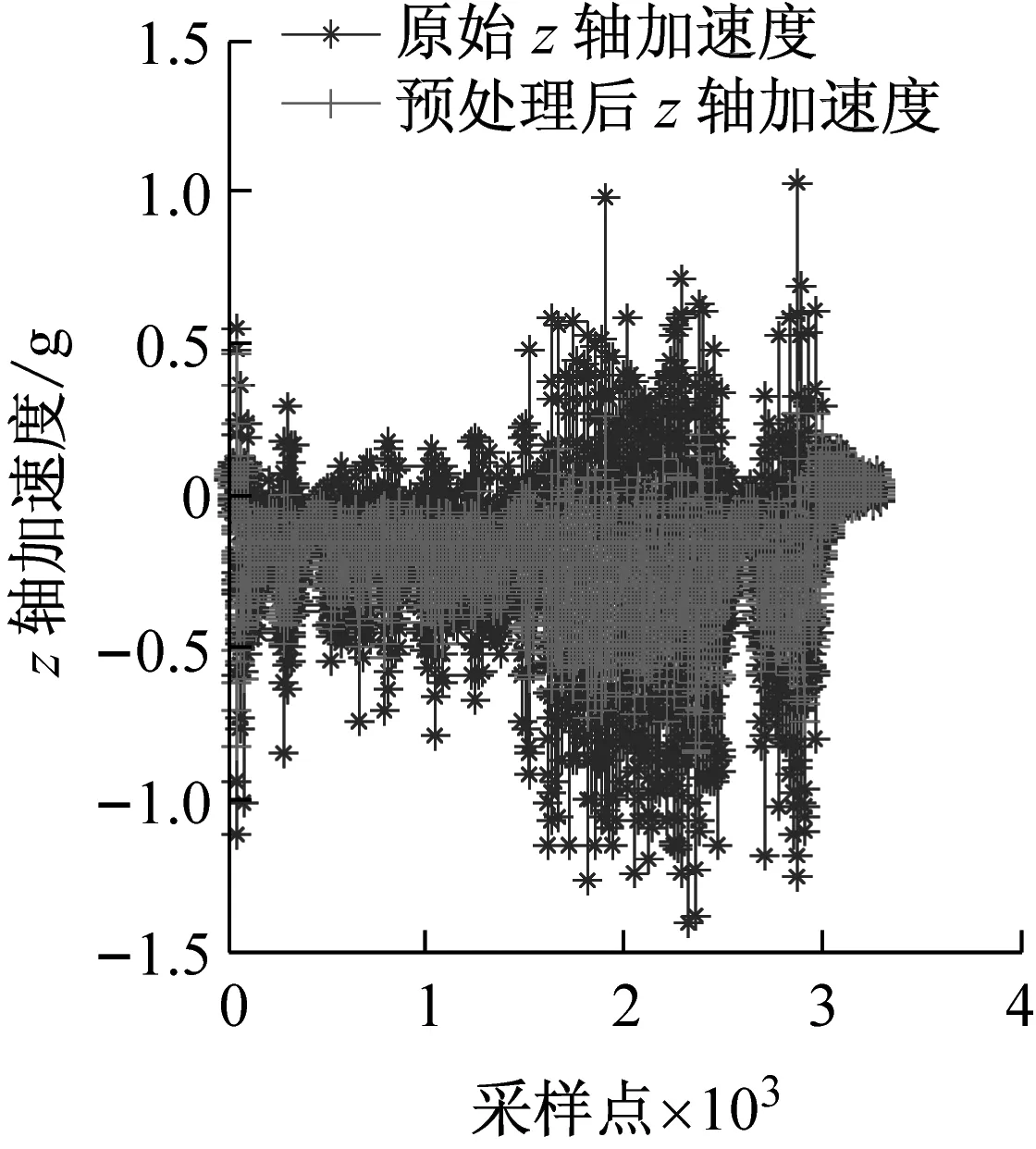
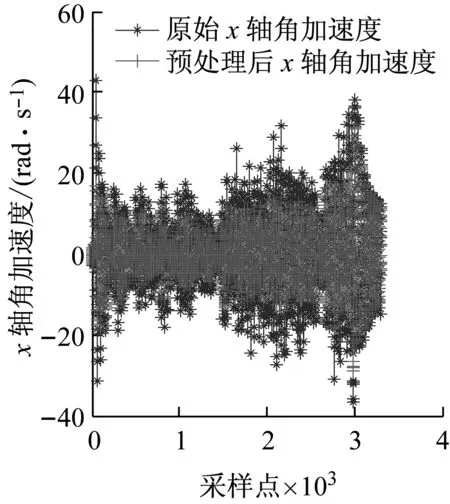
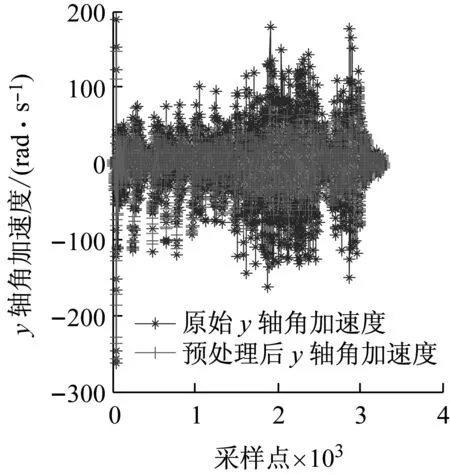
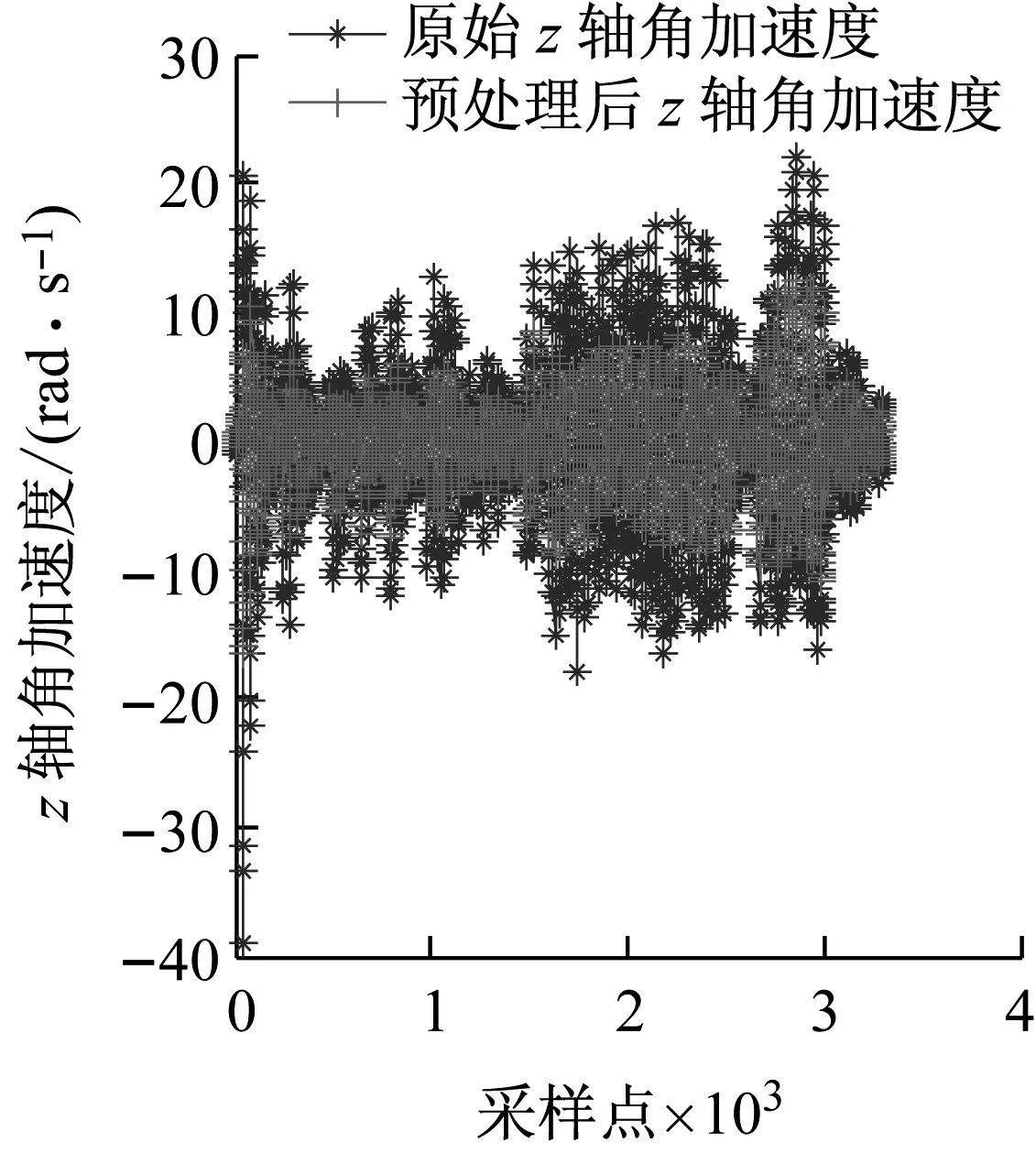
图4 原始数据及预处理结果Fig.4 Raw data and preprocessing results
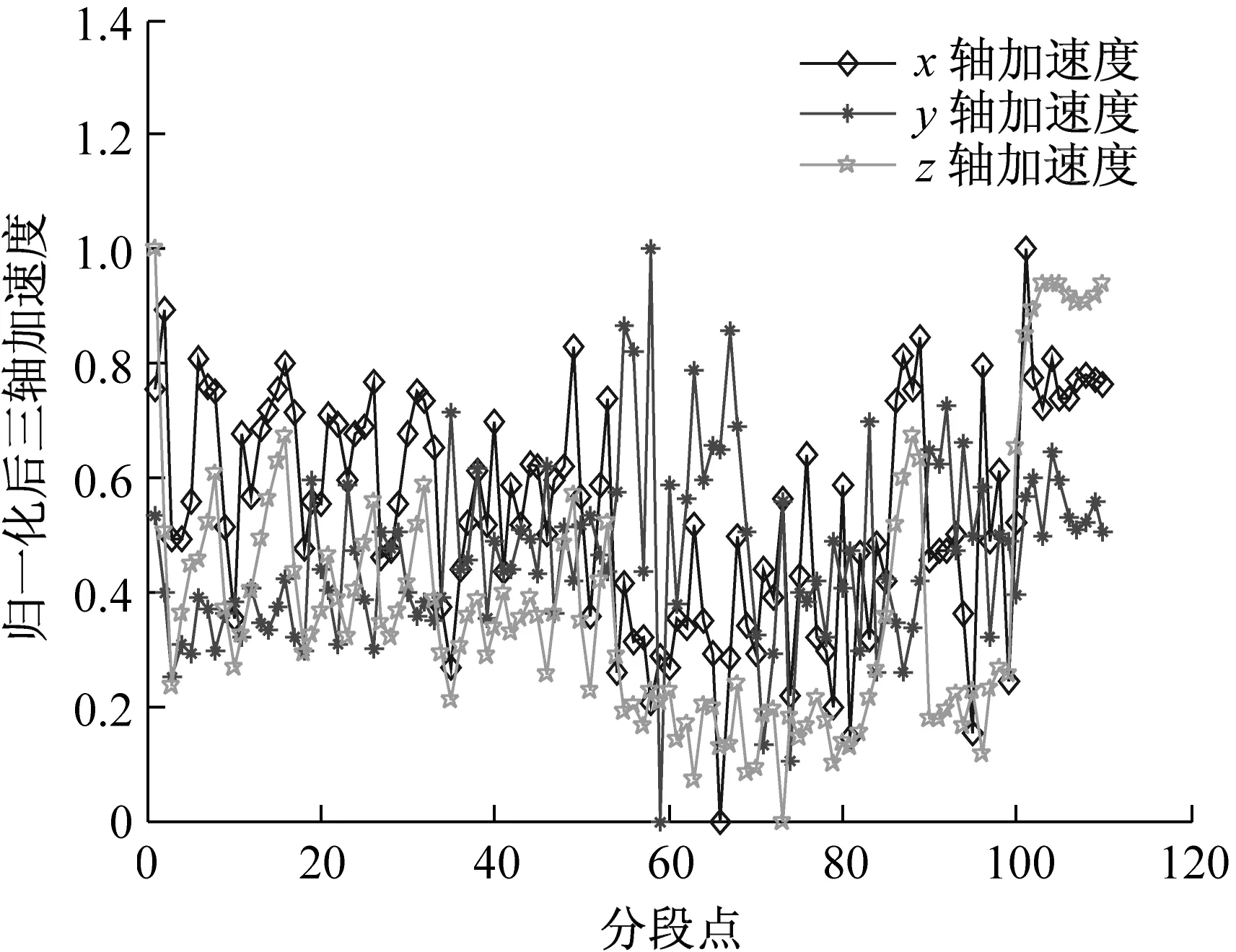
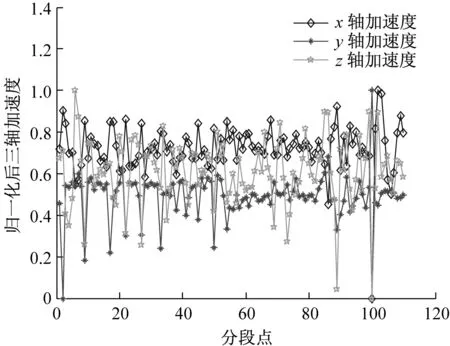
图5 归一化后三轴加速度和三轴角速度Fig.5 Normalized triaxial acceleration and angular velocity
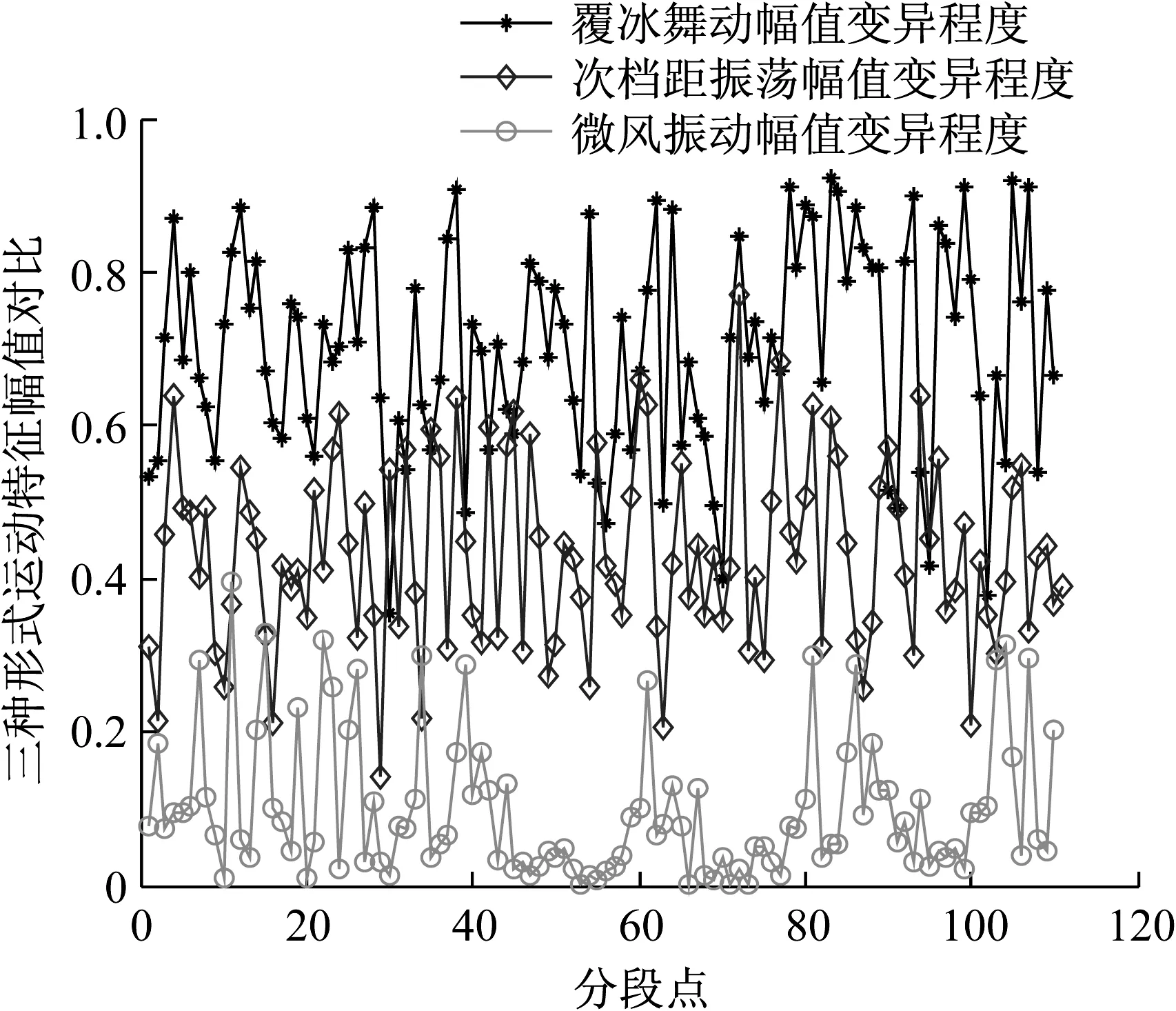
图6 三种运动形式幅值变异程度对比图
Fig.6 Amplitude variation degree comparison diagram of three motion modes
4 总 结
针对现有输电导线运动检测方法的缺点,从新的角度对导线覆冰运动进行检测:采用MEMS惯性传感器,既兼顾了导线自激振荡和扭转引起的运动对覆冰测量的干扰,也解决了单独使用加速度传感器产生扭转误差的问题;采用多维时间序列解决了一维时间序列或合加速度序列进行识别割裂了输电导线整体运动信息;采用对相关系数矩阵进行加权奇异值分解的方法,降低了维数,提高了覆冰运动识别的准确性。实验结果表明,使用本文所提算法能够识别导线运动情况并估计幅频变化程度,且实施方案简单易行,无累计误差,可为长期测量某地区输电线路运动状态提供参考,进一步为输电线路阻尼器的设计提供参数。
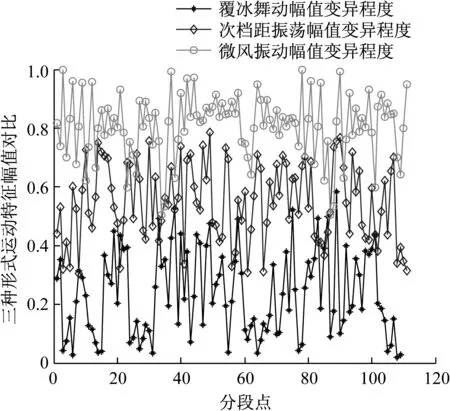
图7 三种运动形式频率变异速率对比图
Fig.7 Frequency variation degree comparison diagram of three motion modes
