悬挂管柱正弦向螺旋屈曲转变时的临界载荷研究

张 强， 蒋 豹， 崔 巍， 刘巨保， 朱 昱

(东北石油大学 机械科学与工程院，黑龙江 大庆 163318)

受井筒约束的悬挂管柱，在其自身重力作用下，井底受压，易丧失弹性稳定性，导致屈曲。例如钻柱屈曲会引起钻头方向改变，加大侧向力和摩阻力，使钻柱自锁，更有甚者导致钻具疲劳破坏。

Lubinski[1]首先研究了钻柱在垂直井筒中的稳定性，导出了钻柱在垂直平面内的弯曲方程，并给出了该方程的级数解。在两端铰支边界约束条件下，采用梁柱模型，无量纲长度取8，给出了钻柱在垂直平面内发生一次弯曲和二次弯曲的临界载荷，分别为1.94和3.75。但他在第2年发表的论文[2]中，将对应的临界载荷改成2.04和4.05，在之后的40余年，我国石油工程行业一直沿用他第2年的数值。后来，韩志勇[3]回顾了Lubinski有关垂直井钻柱屈曲理论在我国的应用情况，对一次弯曲和二次弯曲的临界载荷进行了考证，其临界载荷应该改回1.94和3.75。

Lubinski等[4]假定管柱屈曲成空间螺旋线，屈曲构型为均匀螺旋线并与井壁连续接触，利用最小势能原理，推导了等螺距和轴向压力的关系式，他的这一研究成果得到了石油工程行业的广泛应用。但是，由于自重的影响，实际管柱空间螺旋屈曲构型是一个非等距的螺旋线。为此，研究者们[5-8]采用微分法、能量法、实验法和有限元等方法，对非等螺距的临界载荷进行了广泛的研究，得出了各自不同的临界载荷值。无论是等螺距还是非等螺距假设，均是在螺旋屈曲之后形成一个螺距时得出的临界载荷，其值明显大于正弦屈曲之后刚螺旋屈曲时的临界载荷。

由于管柱的螺旋屈曲发生在初始正弦屈曲之后，经过稳定的正弦屈曲构型阶段之后的又一种稳定的屈曲平衡状态。所以，正弦屈曲向螺旋屈曲转变的过程是非常复杂的。这一过程中，屈曲构型随着井底压力而发生跳跃性变化，管柱与井筒存在接触和脱离等力学行为，使得问题非常复杂。

近年来，研究者们考虑瞬态效应的影响，研究了弹性压杆的动力屈曲问题[9-11]。由于悬挂管柱在井下是缓慢上提或下放的，其动力屈曲并不明显，研究者们普遍将此问题处理成静力屈曲问题。

Gao等[12]展望了悬挂管柱螺旋屈曲问题的研究方法，提出了悬挂段采用梁柱模型，连续接触段采用微分方程的研究设想。Huang等[7]根据这个研究设想，假设将悬挂段分成了4段，用相应的连续性条件、边界条件和稳定性条件，将管柱屈曲问题转化为一个非线性方程组。用迭代法求解这些方程，得到了悬挂管柱平面正弦屈曲、三维螺旋屈曲、连续接触螺旋屈曲和形成一个螺距的螺旋屈曲临界载荷。

本文摒弃了预先指定的管柱屈曲挠曲线假设，考虑井筒内悬挂管柱的几何和接触双重非线性特性，根据井筒内悬挂管柱屈曲分析的有限元平衡方程，采用漫动力法，进行有限元计算，分析悬挂管柱从正弦向螺旋转变时的屈曲构型和临界载荷。

1 模型建立

1.1 模型简化

(1) 悬挂管柱在井筒内的初始状态是完全竖直的。

(2) 将管柱和井筒处理成圆形等截面，忽略接头等部件对屈曲的影响。

(3) 管柱与井筒之间有初始环空间隙存在，管柱变形前轴线与井筒轴线完全重合。

(4) 考虑管柱上端悬挂拉力和管柱自身的重力载荷作用，管柱上端受拉下端受压。

(5) 管柱底部和顶部的边界约束处理成铰支约束。

(6) 管柱处于线弹性状态，假设悬挂管柱为大柔度杆或细长杆。

(7) 管柱屈曲后与井筒内壁面接触，考虑接触力的影响，但不考虑管柱与井筒之间的摩擦力。

(8) 研究管柱静力屈曲的最终稳定状态，忽略管柱上提下放过程中的瞬态影响。

1.2 力学模型

井筒内悬挂管柱的上端受拉，管柱的下端位于井底，在自重作用下受压，建立的悬挂管柱力学模型如图1所示。图1(a)为悬挂管柱长度、载荷和边界示意图，铰支约束边界条件为上端约束x、y方向的平动自由度和绕z轴的转动自由度，下端约束x、y和z方向的平动自由度。

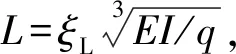
悬挂管柱上端的悬挂拉力为

(1)

式中：E为悬挂管柱的弹性模量；I为悬挂管柱横截面对轴的惯性矩；受拉段的无量纲长度ξT也称为无量纲悬挂拉力。

悬挂管柱下端约束了z方向的平动自由度，其轴向约束反力为管柱受到的向上的压力，其值为

(2)

式中：受压段的无量纲长度ξC也称为无量纲井底压力。

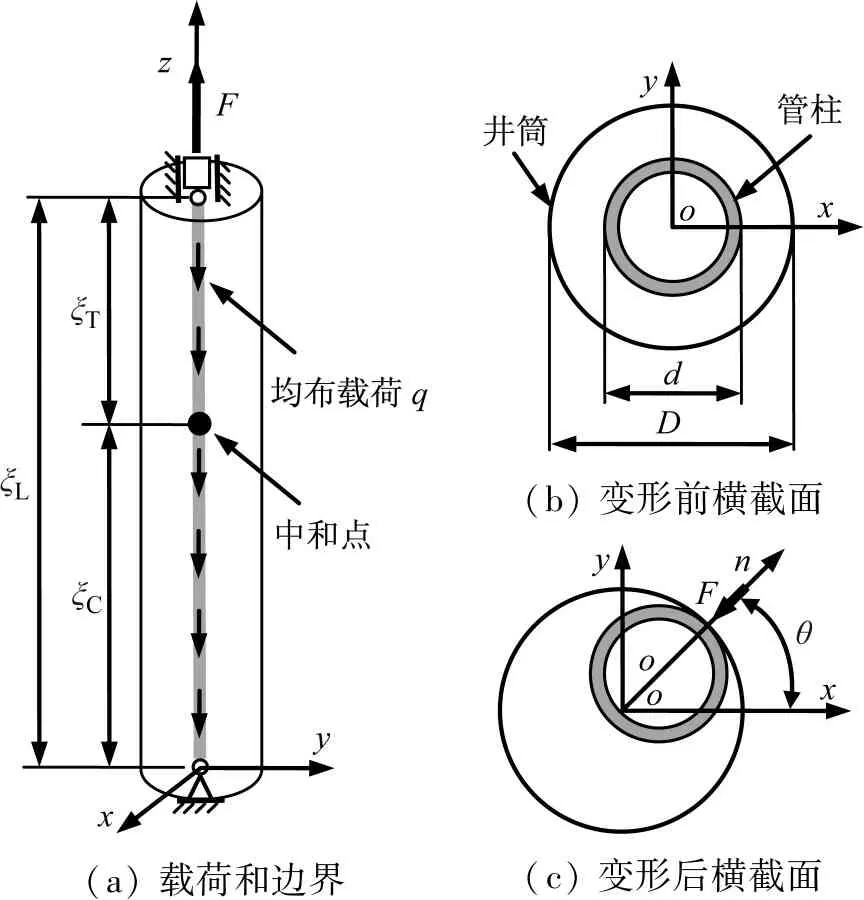
(a) 载荷和边界(b) 变形前横截面(c) 变形后横截面

图1 悬挂管柱力学模型

Fig.1 Mechanical model of suspended tubular string

管柱变形前，由图1(b)可计算出管柱初始间隙为δ=(D-d)/2，d为管柱外径，D为井筒内径。管柱在缓慢下放过程中，上端的悬挂拉力减小，下端的压力增大。当管柱受压段的压力达到一定数值后，管柱丧失稳定性而屈曲变形，产生横向位移和较大的转动变形，横向变形后管柱的圆心为o′，见图1(c)所示，设横向位移量为(u,v)，对应的圆周角为θ。此时力与变形的关系不再是线性，非线性效应突出，属于几何非线性问题。

管柱在横向弯曲变形过程中，受到井筒约束，将与井筒内壁面接触，设接触时的接触力为Fn。在任一轴向距离、任一圆周方向上均可能产生接触和脱离的力学行为，属于接触非线性问题。

综上所述，悬挂管柱屈曲力学模型归结为几何和接触双重非线性问题，这样处理使得悬挂管柱屈曲力学分析更趋于合理。

1.3 屈曲静力学方程

采用有限元法，依据间隙元理论[13]，经过梁单元和间隙元的拼装，可得管柱几何和接触非线性静力屈曲分析的总体平衡方程式为

(K0+Kσ(u)+Kn(u))u=Fq+Fn(u)

(3)

式中：K0为悬挂管柱的线弹性刚度矩阵；Kσ(u)为悬挂管柱的几何刚度矩阵；Kn(u)为悬挂管柱的接触刚度矩阵；u为悬挂管柱的节点位移向量，包括3个方向的平动和3个方向的转动自由度，u=[u,v,w,θx,θy,θz]T；F为悬挂管柱的节点载荷向量，F=Fq+Fn(u)；Fq包含上端悬挂拉力和管柱自重均布载荷；Fn(u)为管柱的接触力向量。式中的几何刚度矩阵、接触刚度矩阵和接触力向量是节点位移的函数。

2 计算方法

2.1 慢动力法

采用有限元法，对式(3)进行双重非线性静力屈曲计算，但还存在收敛困难和算法不稳定等问题。表现在如下方面：

(1) 由于悬挂管柱的从正弦屈曲到螺旋屈曲的构型存在跳跃性变化，管柱与井筒之间存在接触和脱离等强非线性力学行为，导致计算过程中接触状态突变，易引起计算异常终止，存在收敛困难。还表现在悬挂管柱屈曲后，挠度突然增大，不能识别出接触状态，管柱穿透出井筒壁面，导致计算失败。

(2) 算法不稳定表现在收敛解不唯一，悬挂管柱屈曲的构型存在随意性。例如，形成平面正弦屈曲构型后，随着上端拉力的减小，下端压力的增加，平面正弦屈曲构型在井筒内旋转，却不能形成空间螺旋屈曲构型；由于对管柱悬挂拉力载荷增量和载荷步长的敏感性，时而形成时而又不能形成空间螺旋屈曲构型；即使形成了空间螺旋屈曲构型，但又重新回到平面正弦屈曲构型；形成空间螺旋屈曲构型后，在不同轴向位置处，可能同时存在右螺旋和左螺旋的屈曲构型。

为了解决井筒内悬挂管柱从正弦屈曲向螺旋屈曲过程的收敛困难和算法不稳定性问题，提出悬挂管柱非线性静力屈曲分析的慢动力法。该方法是利用动力学方法，按照一定方式施加自重和悬挂拉力等恒定外载荷，引入惯性力和阻尼力，考虑时间积分效应，设置较大的虚拟阻尼，计算一定的时间，求解悬挂管柱动力响应直至稳定。也就是利用动力学方法，解决悬挂管柱静力屈曲问题[14]。

采用慢动力法，悬挂管柱屈曲的动力学基本运动方程为

Mu″+Cu′+Ku=F(t)

(4)

式中：M为悬挂管柱的质量矩阵；C为悬挂管柱的阻尼矩阵；K为悬挂管柱的刚度矩阵，K=K0+Kσ(u)+Kn(u)；u′和u″分别为悬挂管柱的节点速度和加速度向量；t为计算时间；F(t)为悬挂管柱的节点载荷向量，与方程(1)中的载荷相同，只是考虑了载荷施加的时间历程，F(t)=Fq(t)+Fn(u)(t)。

采用Newmark直接积分法，对式(4)进行隐式有限元求解。若t时刻悬挂管柱的位移、速度和加速度已知，则可计算出t+Δt时刻悬挂管柱的动力响应。随着计算时间的延长，悬挂管柱屈曲构型趋于稳定，悬挂管柱各节点无速度和加速度，方程(4)可退化成方程(3)，实现用慢动力法对悬挂管柱静力屈曲的求解。

2.2 外载荷

为了减小管柱上端悬挂拉力FH和自重均布载荷q对管柱的动力冲击，采用正弦波方式，施加随时间变化的外载荷，如图2所示。上端悬挂拉力FH施加的方式为：①在管柱1/4倍固有周期之前，施加正弦波的悬挂拉力；②在管柱1/4倍固有周期之后，施加恒定的悬挂拉力。

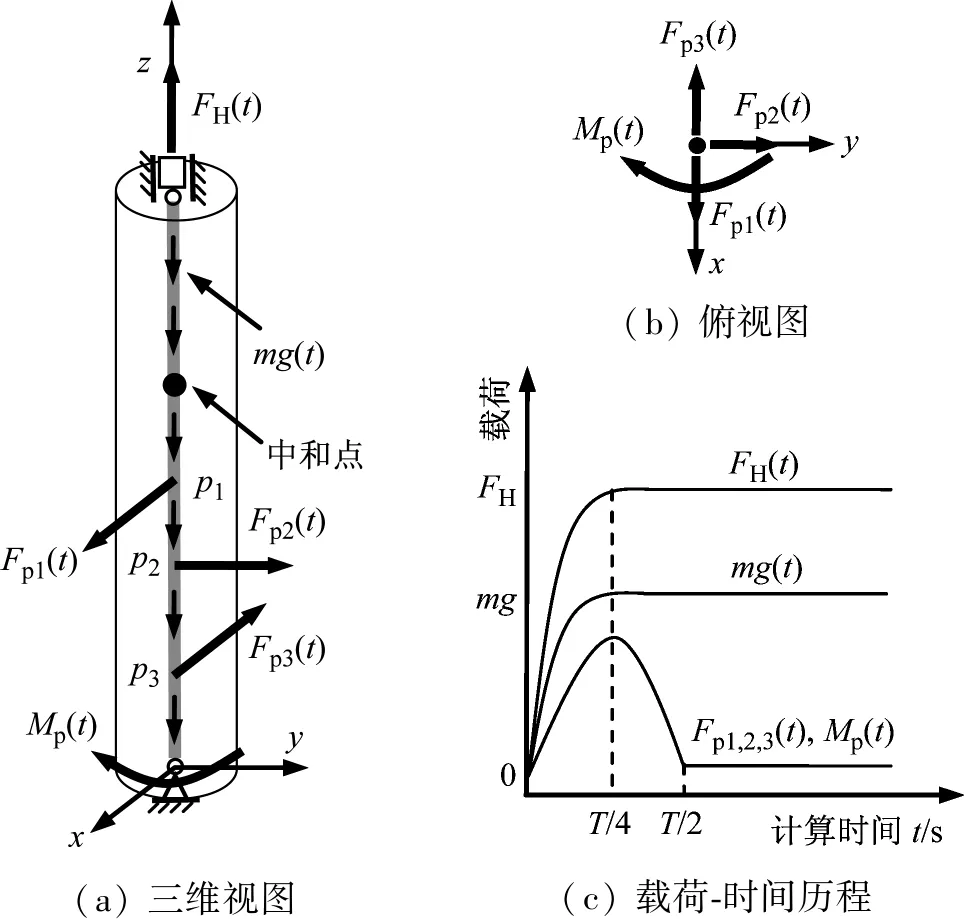
(a) 三维视图(b) 俯视图(c) 载荷-时间历程

图2 外载荷和扰动力的施加方式

Fig.2 The mode of external load and disturbance load

同理，为了施加管柱自重载荷，施加的重力mg也采用同样的正弦波方式。

2.3 扰动力

由于初始几何缺陷会影响管柱屈曲的临界载荷，而微小扰动力是在初始施加，在后续分析中撤销，不会影响管柱屈曲的临界载荷。本文采用初始扰动力方式，既保持了管柱结构的完整性，又实现了初始缺陷的施加。

为了易形成空间螺旋屈曲构型，在初始扰动力的施加过程中，使管柱变形成空间曲线，将悬挂管柱受压段长度均分4段，每1/4长度处(p1、p2和p3位置)施加互成90°的扰动力Fp，管柱下端施加1个扰动扭矩Mp。施加扰动力的大小均为单位载荷，扰动力施加的方式如图2所示。在管柱1/2倍固有周期之前，施加正弦波的扰动力；在管柱1/2倍固有周期之后，施加的扰动力为0。

2.4 阻尼比

方程(2)中的阻尼矩阵C一般为常用的Rayleigh阻尼，也就是比例阻尼，它包括α质量阻尼和β刚度阻尼。本文选取α质量阻尼，阻尼矩阵C=αM。以管柱第1阶的固有频率ω作为模态阻尼比，根据正交性原理，得到α质量阻尼与阻尼比ζ的关系为

α=2ωζ

(5)

采用慢动力分析法计算时，选取合适的阻尼比，得到质量阻尼，输入方程(4)中，进行慢动力计算。

2.5 计算流程

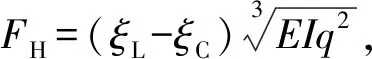
图3 计算流程框图Fig.3 Flowchart of calculation flow

对悬挂管柱屈曲的动力学基本运动方程(2)进行有限元计算，计算总时间取n个周期，周期取第1阶自振周期。计算结束后，判断管柱各节点的挠度u是否随时间变化。若是，表明管柱各节点还有速度u′和加速度u″，存在附加的惯性力Mu″和阻尼力Cu′，应减小阻尼比ζ，重新计算，直到管柱各节点的挠度u为常值，实现屈曲构型稳定。然后判断挠曲线是否是空间螺旋屈曲构型，若不是，增加受压段无量纲长度ηC重新计算，直到得到稳定的空间螺旋屈曲构型。

3 计算结果与分析

3.1 计算参数

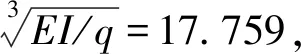
3.2 无接触正弦屈曲临界载荷分析

将空间悬挂管柱简化成平面问题，除了上下两端铰支约束外，还约束管柱所有节点y方向的平动自由度和绕x方向的转动自由度。不考虑与井筒的接触，研究悬挂管柱无接触的正弦屈曲问题。将图3计算流程中的螺旋屈曲构型判断改成正弦屈曲构型，进行有限元计算。将施加扰动力在1/4固有周期时刻的最大挠度进行无量纲化，即u/u|t=0.25T=1，图4给出了平面模型悬挂管柱最大挠度位置处的挠度曲线。

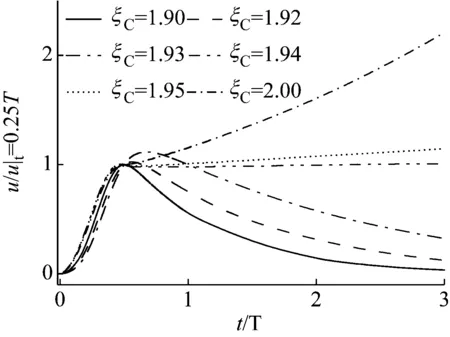
图4 悬挂管柱平面模型的挠度曲线Fig.4 Deflection curve of suspended tubular string in plane model

由图4可见，当井底压力ξC<1.94时，悬挂管柱挠度随横向扰动力的撤销而逐渐减小，悬挂管柱处于稳定平衡状态；当井底压力ξC=1.94时，悬挂管柱挠度随横向扰动力的撤销保持不变，悬挂管柱处于随遇平衡状态；当井底压力ξC>1.94时，悬挂管柱挠度随横向扰动力的撤销而逐渐增大，悬挂管柱处于不稳定状态。由此可见，本文计算得到的悬挂管柱平面正弦屈曲的临界压力ξC=1.94。文献[1]的结果ξC=1.94，文献[7]的结果ξC=1.89，本文结果与文献[1]吻合，比文献[7]大了2.65%，验证本文计算方法的正确性。

3.3 有接触的正弦屈曲过程分析

按照3.2节平面模型，同时考虑悬挂管柱与井筒的接触，研究其正弦屈曲过程。将悬挂管柱在井筒内x方向的变形无量纲化，与井筒接触时的x正方向横向变形量记为1，对应的x负方向记为-1，图5给出了不同井底压力下的挠曲线。

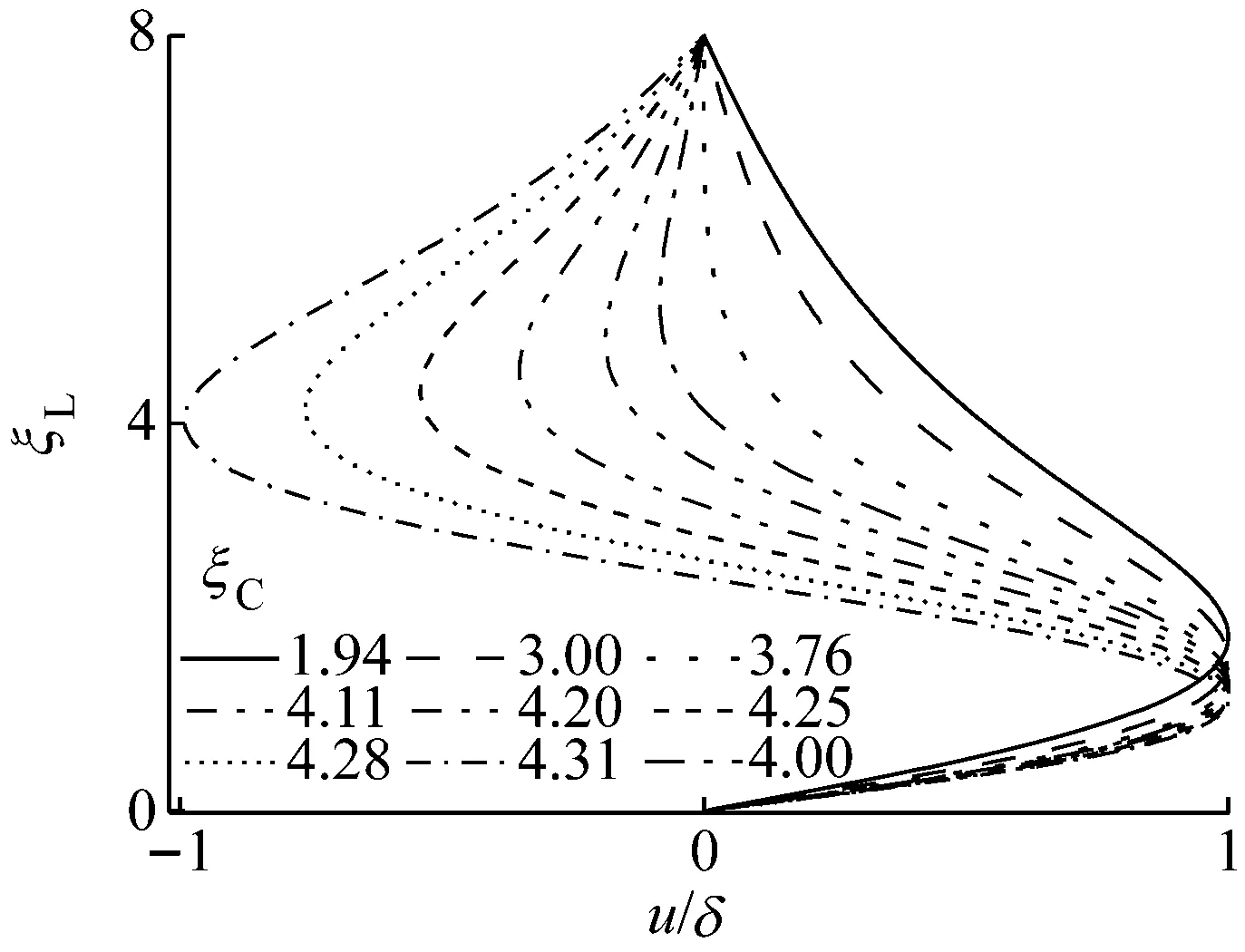
图5 平面模型中一次弯曲和二次弯曲的挠曲线Fig.5 First order and second order buckling in plane model

由图5可见，由于井底压力ξC=1.94时悬挂管柱处于随遇平衡状态，考虑井筒约束后，将与井筒接触，接触点位于ξL1=1.80处，挠曲线为一次弯曲状态。当井底压力ξC=3.76时，悬挂管柱下段在x方向为正值，悬挂管柱上段在x方向刚出现极小的负值，接触点位于ξL1=1.41处，挠曲线为二次弯曲状态。井底压力ξC=3.76为二次弯曲临界载荷，与文献[1]的结果ξC=3.75基本吻合。

随着井底压力的增加，悬挂管柱下段接触点逐渐下移，上段x负方向的挠度逐渐增大。当井底压力ξC=4.31时，悬挂管柱上段刚好与井壁接触，上段接触点位于ξL12=4.03处，下段接触点位于ξL1=1.10处，挠曲线为完全二次弯曲状态。

3.4 螺旋屈曲分析

(a) p1位置

(b) p2位置

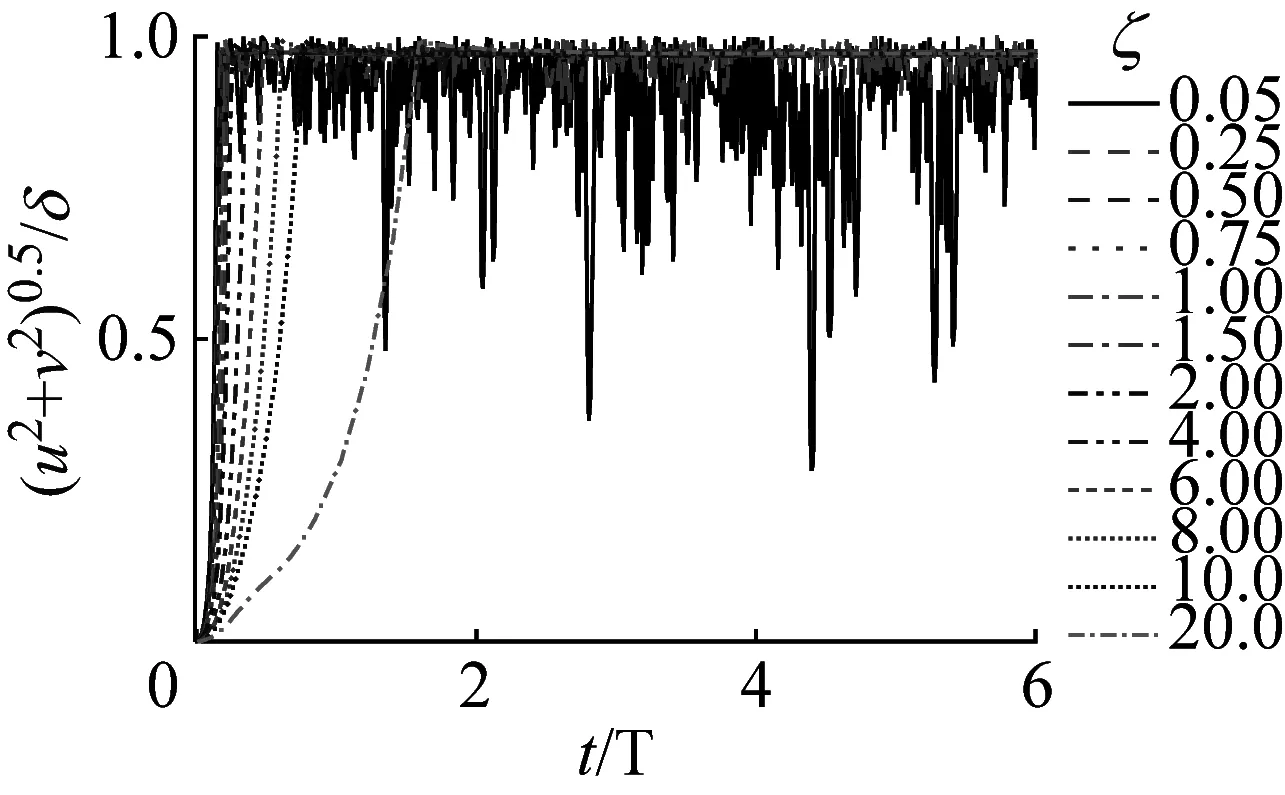
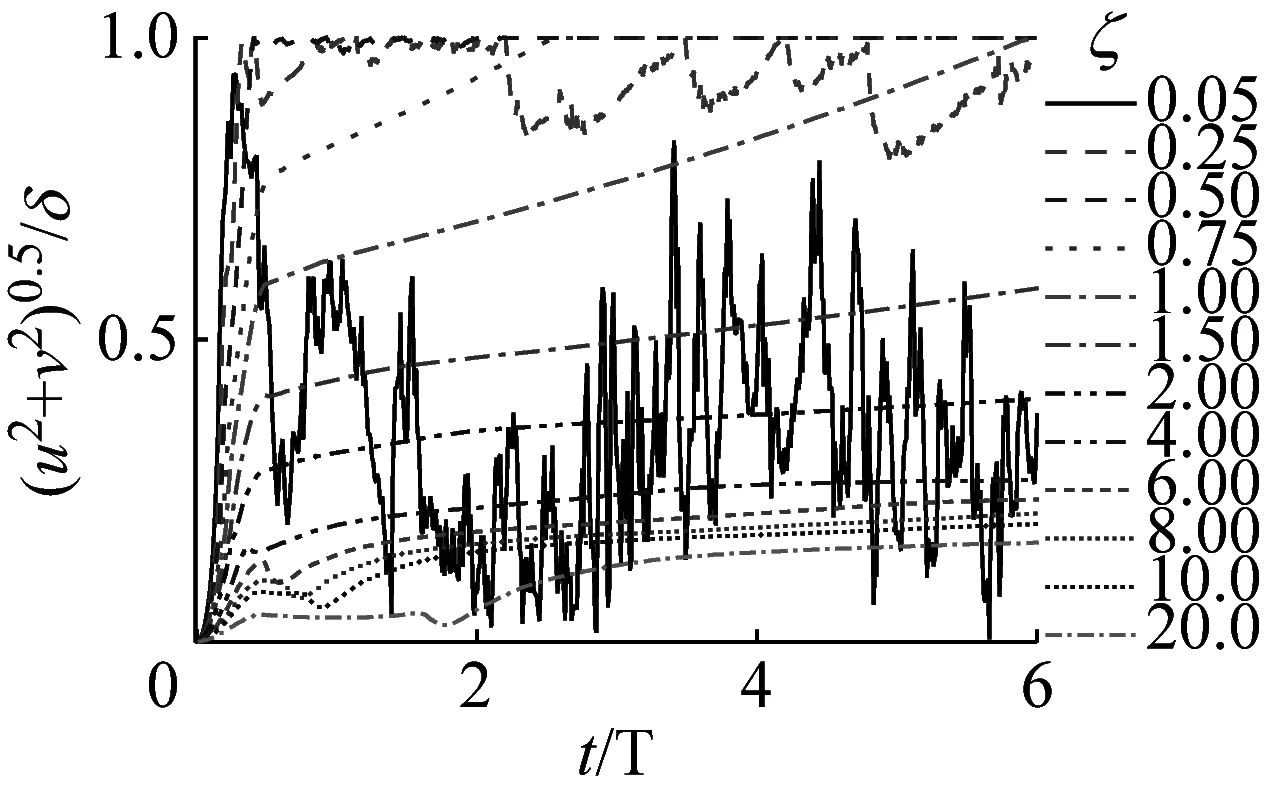
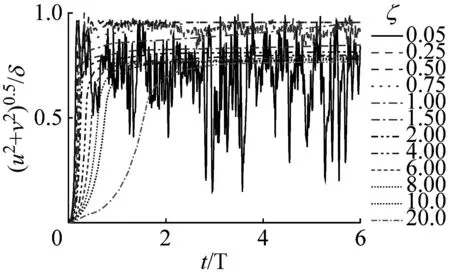
(c) p3位置图6 井底压力ξC=4.11时阻尼比对挠度的影响Fig.6 Influence of damping ratio on deflection when ηC=4.11

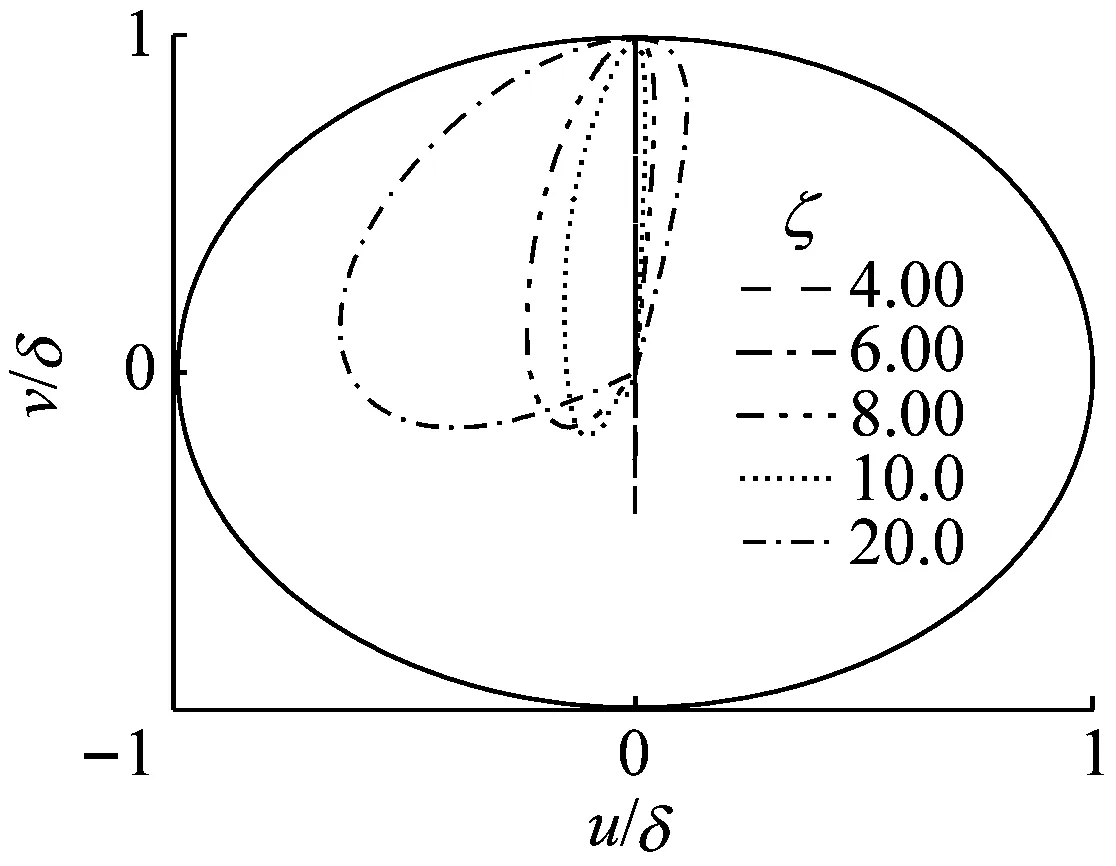
(a) ξC=4.10

(b) ξC=4.11

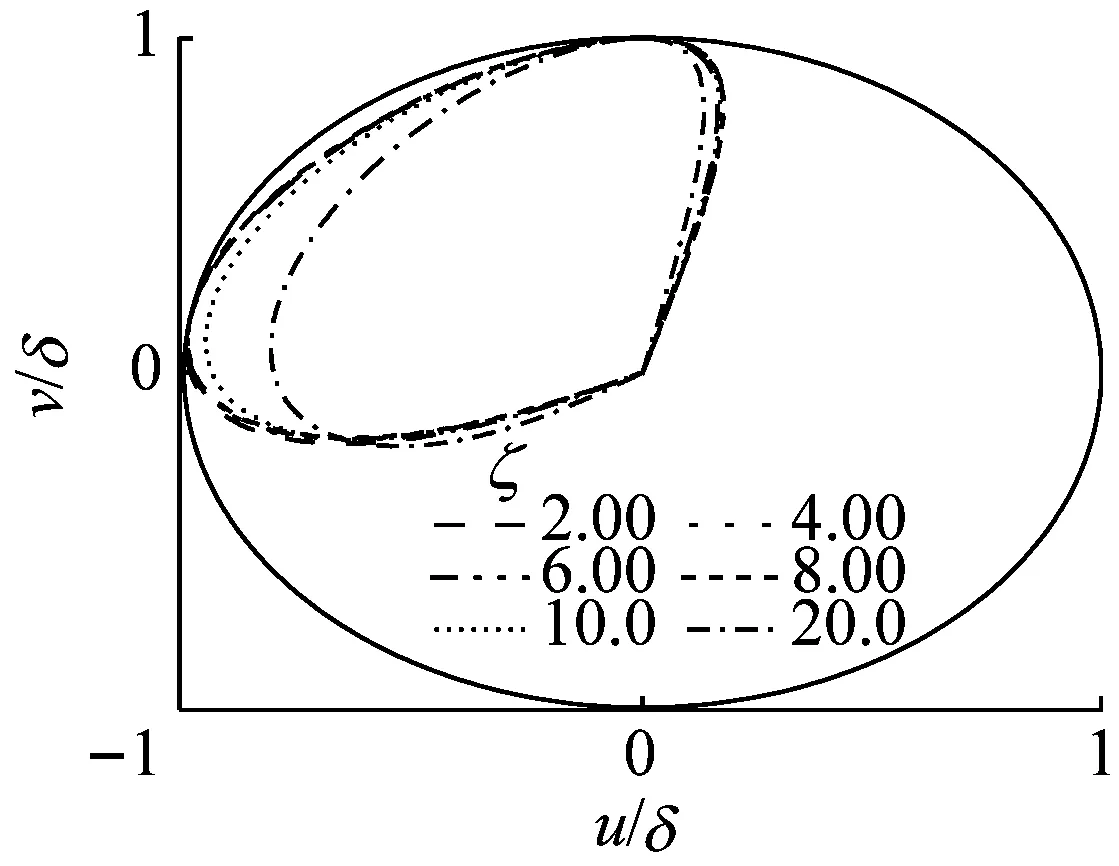
(c) ξC=4.12图7 阻尼比对屈曲构型的影响Fig.7 Influence of damping ratio on buckling configuration

由图6可见，①阻尼比取1.50≤ζ≤20.0，在6个周期内，管柱在p2和p3位置处的挠度在3个周期后均处于稳定状态，但在p1位置的挠度在6个周期时间内一直在持续增加。由此可见，在大阻尼比条件下，虽然横向挠度曲线不随时间剧烈震荡，计算容易收敛，但使动力响应处于稳定、达到常值状态的时间会延长，也影响计算收敛效率。②当阻尼比ζ=1.00时，管柱在p1和p2位置的挠度在6个周期内刚好稳定，在p3位置的挠度在1个周期内处于稳定；当阻尼比ζ=0.75时，管柱在p1和p2位置的挠度在2个多周期内处于稳定，在p3位置的挠度在1个周期内处于稳定；当阻尼比ζ=0.50时，管柱在p1、p2和p3位置的挠度在1个周期内均处于稳定。由此可见，阻尼比取0.50≤ζ≤1.00，在6个周期内，管柱的挠度均能处于稳定、达到常值状态。③当阻尼比ζ≤0.25时，管柱在这3处位置处的挠度出现持续震荡。阻尼比越小，振动越剧烈。在p1位置，管柱与井筒出现时而接触碰撞，时而脱离井筒的现象。由此表明，取较小的阻尼比时，挠度难以处于稳定、达到常值状态，计算难收敛。

通过图6中阻尼比对挠度的影响分析可见，在给定的井底压力和计算时间范围条件下，为了获得稳定的屈曲构型，应该先取较大的阻尼比，然后逐渐减小阻尼比，直到悬挂管柱的挠度趋于稳定、达到常值状态为止。但是阻尼比过小，易引起管柱剧烈振动，在给定的计算时间范围内，计算难收敛。

从图7可见，①井底压力取ξC=4.10，阻尼比较大时(8.00≤ζ≤20.0)，xy平面投影为不同形状的曲线；当阻尼比ζ为4.00和6.00时，xy平面投影为直线且重合，为稳定的平面正弦屈曲状态，表明井底压力ξC=4.10时屈曲变形为正弦构型。②井底压力取ξC=4.11，阻尼比较大时(1.50≤ζ≤20.0)，xy平面投影也为不同形状的曲线，但是屈曲变形并没有处于稳定、达到常值的状态(见对图6的分析)；当阻尼比ζ为0.75和1.00时，xy平面投影为曲线且重合，管柱上存在2点与井筒接触，为稳定的螺旋屈曲状态，表明井底压力ξC=4.11时屈曲变形刚好从正弦突变成螺旋构型。③井底压力取ξC=4.12，阻尼比较大(10.0≤ζ≤20.0)时，xy平面投影也为不同形状的曲线；当阻尼比较小时(2.00≤ζ≤8.00)时，也得到了稳定的螺旋屈曲状态，表明井底压力ξC=4.12时屈曲变形为螺旋构型。

在6个周期的计算时间范围内，图8给出了阻尼比ζ对计算效率的影响，整体来看，计算耗费的CPU时间随着阻尼比的增大而逐渐缩短。但从对图6的分析可见，阻尼比过小或过大均影响计算的稳定性。其中临界载荷ξC=4.10时，由于处于正弦屈曲构型向螺旋屈曲转变的前一个临界载荷，屈曲构型极不稳定，计算耗费的CPU时间较长。

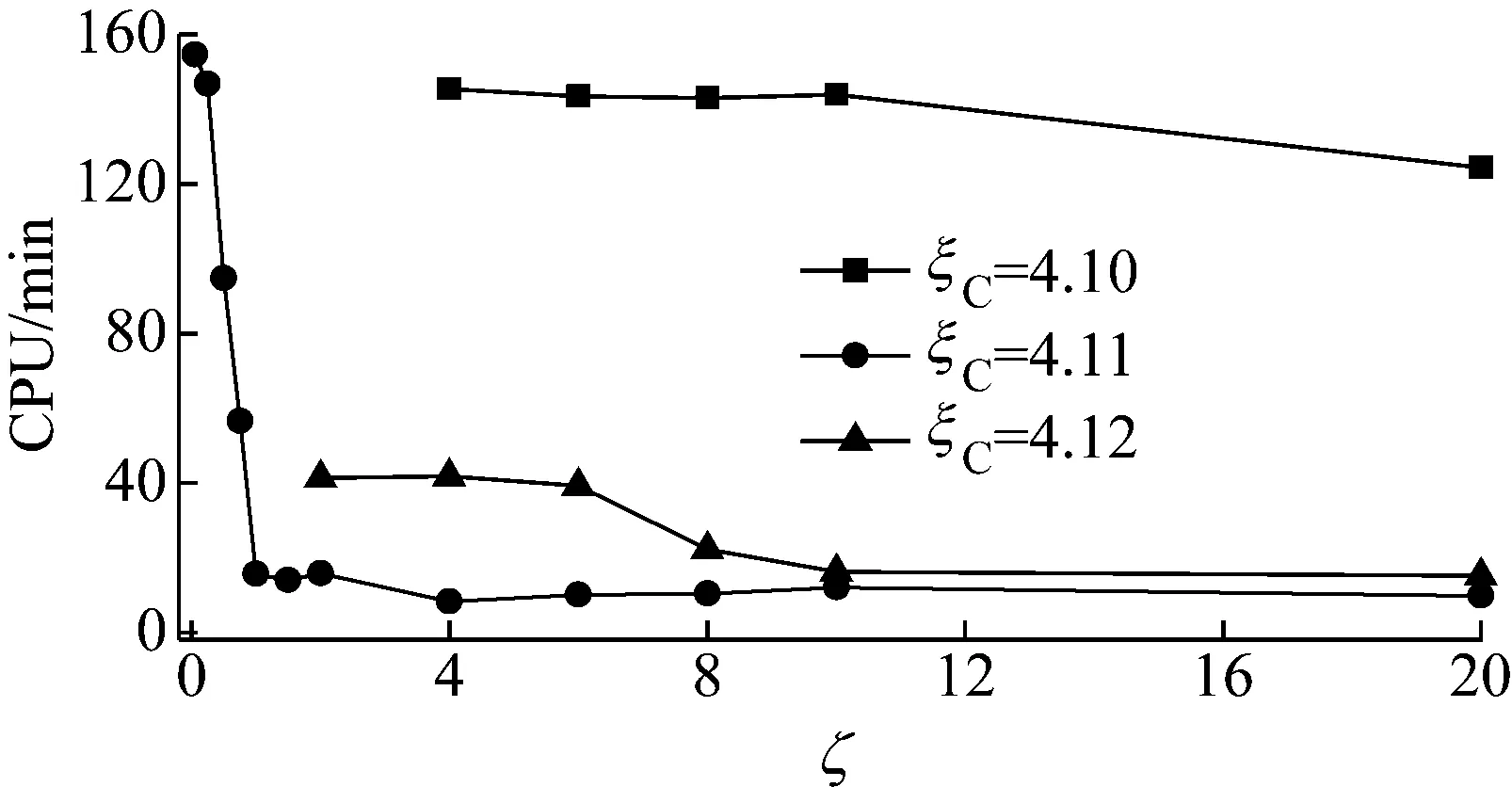
图8 阻尼比ζ对计算效率的影响Fig.8 Influence of damping ratio on computational efficiency

综上可见，本文计算得到的悬挂管柱平面正弦屈曲向空间螺旋屈曲转变时的临界载荷为ξC=4.11。文献[7]的结果为ξC=4.00，本文的结果比文献[7]大了2.75%。

根据图7的计算结果，图9给出了悬挂管柱从正弦屈曲到螺旋屈曲的三维空间屈曲构型。由图9可见，①当井底压力ξC≤4.10时，悬挂管柱的屈曲构型为一平面，为平面正弦屈曲状态。②当井底压力ξC=4.11时，悬挂管柱的屈曲构型突变成空间螺旋曲线，为空间螺旋屈曲构型。2个接触点的轴向位置分别为ξL1=1.30和ξL2=3.13，螺旋段长度为ξL2-ξL1=1.83，螺旋角度为θL2-θL1=77.9°。③当井底压力ξC>4.11时，螺旋屈曲构型进一步扩展，当井底压力ξC=4.31时，悬挂管柱在平面模型中为完全二次弯曲状态，但在三维模型中早已成为空间螺旋屈曲状态。

本文无量纲长度取ξL=8，计算得到了悬挂管柱正弦屈曲向螺旋屈曲转变时的临界载荷。根据文献[7]，由于管柱越长管柱柔度越大，可以预见对应的临界载荷会随着管柱长度的增加而逐渐减小，最后趋于常值。

图9 三维空间的屈曲构型Fig.9 Buckling configurations in three dimensional space

4 结 论

本文基于慢动力有限元法，对悬挂管柱进行了正弦屈曲向螺旋屈曲转变时的临界载荷研究，得出如下结论：

(1) 正弦屈曲向螺旋屈曲转变是一个屈曲构型突变的过程，采用慢动力有限元法，将静力屈曲问题转换成动力学问题。按照正弦波的方式施加外载荷和扰动力，通过虚拟较大的阻尼比，对井筒内悬挂管柱后屈曲分析的收敛和算法的稳定性具有重要的作用。阻尼力能够有效地抑制管柱振动，在6个固有周期的计算时间范围内，管柱的挠度均能处于稳定、达到常值状态，可以得到悬挂管柱稳定的屈曲构型和临界载荷。

(2) 无量纲长度取8，悬挂管柱正弦屈曲向螺旋屈曲转变时的临界载荷为4.11，螺旋屈曲的构型中存在两个接触点，螺旋段长度为1.83，螺旋角度为77.9°。悬挂管柱正弦屈曲和螺旋屈曲的临界载荷均比文献[7]大了近3%，但是本文一次弯曲和二次弯曲的临界载荷与Lubinski的研究结果完全吻合，表明本文的结果具有更高的计算精度。

(3) 采用慢动力法，也可以用于诸如定向井和水平井等井型的屈曲分析，计算出稳定的正弦和螺旋屈曲构型以及对应的临界载荷。