贪婪算法与遗传算法结合的建设项目合同优化选择

李霄鹏

（齐鲁工业大学（山东省科学院）管理学院，济南 250300）

0 引言

目前对于工程领域优化的研究集中于对建筑工程的项目调度和资源分配上，并使用传统的解决资源平衡的方法,如CPM关键路径法、网络计划法、启发式算法等来解决不同情境下的资源均衡问题，使用遗传算法、蚁群算法来解决复杂情况下的优化平衡问题等。而对合同资源优化的研究多集中在供应链优化协调领域，如李建斌等[1]、张秀东等[2]采用博弈论等方法研究供应链柔性合同优化问题、徐琪[3]构建了合同与供应链组合优化决策模型等。

对前人研究成果[4-8]分析发现，目前关于资源优化尤其是合同优化的研究主要集中于供应链优化协调，针对建筑工程项目领域合同优化的研究较少。本文在以上研究的基础上，应用背包问题解决合同的优化选择和项目的排序。并在传统遗传算法的基础上进行改进，引入贪婪算法，使用MATLAB语言进行编程仿真，在项目面临的若干个合同中作出最优选择。

1 复杂建筑项目合同优化模型构建

本文采用背包问题原理构建建筑项目合同优化模型。0-1背包问题即从n个物品的集合中选择部分物品，使得物品总价值最大，但总重量不超过背包容量c。将其运用在建设项目合同优化问题上，就是在合同所需资源总和不得超过项目的总预算资源C的前提下，按照计算结果从众多待选合同中选择部分合同，并对其设定履行顺序，进行项目资源的合理分配，使得项目发挥的总效益最高。据此构建目标函数模型如下：

其中pj表示第j个合同带来的项目效益，wj表示第j个合同所耗费的资源，xj=1表示选择第j个合同，xj=0表示不选择第j个合同，C表示项目总预算资源额度。根据0-1背包问题原理，用长度为n的二进制编码，如果项目中选择某个合同，则对应的值为1，否则为0。把待选合同所需资源（k为资源的权重，不同的资源权重不同，一个合同所需资源总和为wjxj）总和作为个体的适应度。据此把项目待选合同按耗费资源数量比进行排序，先将资源耗费少的合同选出，直至总耗费资源接近项目总资源数量，从而形成新的合同优先级方案。

2 合同优化数学模型的遗传算法实现

使用背包问题求解优化方案的算法很多。有的算法比较精确，如常用的分支定界法、动态规划法等算法，有的算法则属于近似算法，如使用蚁群算法、遗传算法、神经网络算法来求解背包问题。本文选择遗传算法进行数据处理和仿真。

2.1 遗传算法及改进

遗传算法简称为GA，它是一种模拟方法，使用数学模型来模仿生物的一系列进化过程。生物进化是通过染色体作为遗传基因的承载体，遗传算法则用一串数组来模拟染色体，并通过对染色体的操作和选取，对问题进行优化以获得相对最优解。它是基于自然进化选择和基因遗传的原理来进行搜索的优化设置，很适合解决优化计算问题，目前已经应用于人口模型构建、工程资源、通讯网络优化等多种领域[11]，还将在解决人工生命的进化模型和复杂系统的模拟设计中进行广泛应用。

虽然遗传算法和编码方法可以方便对背包模型和适应度进行计算，但是在基本遗传算法运算过程中有一定的局限性，在使用交叉变异进行进化得到新的进化种群时，容易出现致死染色体，在迭代进化过程中其获取的解会降低多样性，精确度有限并容易得到局部最优解。为了避免这些问题，目前一般采用罚函数进行迭代处理和优化。但由于使用规模的限制，罚函数不能用于数量较大的问题求解，故可选用其他算法对遗传算法进行改进以求获得合适的最优解。目前对遗传算法进行改进的方法主要有以下几种[12-15]：

（1）将遗传算法与启发式搜索算法贪心算法结合改良性能。

（2）对遗传算法通过禁忌搜索进行变动扩大了搜索主框架。

（3）使用二重结构编码开发混合遗传算法。

（4）将传统算法如杂交与遗传算法相结合。

（5）使用变换算子来代替交叉算子。

本文选择将遗传算法和贪婪算法结合起来进行使用，构建使用背包问题的合同组合优化模型，避免了局部最优解的漏洞，并得出最终最优解[16]。贪婪算法属于启发式算法的一种，每次使用贪婪规则进行决策，其结果都是不可撤销的。贪婪算法没有很多可行解的同步选择，最终只能得到一个最优的可行解。使用贪婪算法进行遗传算法求解，其所获得的解精确度更高，更接近最优解。将其应用在合同选择中，即每次进化选取一个中标合同，直到实现项目资源的完全利用。比较常用的贪婪准则参数是价值密度参数，也称为贪婪策略，即在诸多建筑工程项目投标合同中，选择可以适合项目的价值c/w值最大的合同。

2.2 结合贪婪算法的遗传算法求解流程

本问题求解的流程如下：

（1）通过基因编码将问题空间变成遗传空间。基因编码可以将若干个基因码按照一定的顺序进行排列，其排列顺序就是遗传编码结构。选择二进制编码进行表述，编码串中1表示将选中的投标合同，0表示未选中合同。如“110111”就代表一套合适的分包商选择方案和资源分配方式，它表示选择第1，2，4，5，6号投标合同签订最终协议，并分配合同资源。

（2）使用贪婪算法对初始编码进行修复。基本的遗传算法虽然可以通过对编码串进行操作，从当前的群体中选择出具有优良基因的染色体使其延续下去，但它们并不一定是最满足限制条件的可行解。为了避免产生无效染色体，本文使用贪婪算法对初始形成的编码进行修正来获得合适的最优解。

贪婪算法修复的基本思想为：选定一个合适的参数资源效益比值（C/W)为参照，在项目入围的所有投标合同中，计算待选合同所带来的效益及所耗费的资源的比值，将结果最小的合同选择出来，直到满足项目限定范围的资源限制为止。经过迭代过程可获得一些新的基因编码串，这些新编码串所代表的合同选择相对更优，而且能够满足项目所面临的条件的限制。

（3）选择适应度函数。由于将贪婪算法和遗传算法进行结合，弥补了遗传算法中产生无效染色体的情形，故不必使用罚函数法，而是确定适应度函数对个体的适应度进行计算，并进行进化和淘汰。背包问题中常用的适应度值是物品价值和目标值，本文直接选取目标值作为适应度函数值，公式为：

（4）轮盘赌选择。

对于基因的选择方法有很多。本文采用轮盘赌方法进行选择。为了避免适应度函数为负值并防止有效信息的丢失，使用公式fi(i)=fit(i)-min(fit)+1对适应值进行处理，以获得合适的信息。

（5）使用交叉概率参数进行交叉。本文采用交叉概率pc=0.5，并选择一点为交叉点，使用单点交叉方式，随机选取一点作为基因的交叉点，设交叉概率pc=0.5。

（7）对形成的新种群使用迭代方法继续进化下去，直到获得最优组合。

3 算例

本文选取以某大型海外工程设备项目作为算例进行分析，从项目存储的招投标数据集中，选用投标合同100份，作为待选样本。由于不同的投标合同，投标商的资质信用能力各方面存在差异，所消耗的资源种类也有差别。故通过专家评价和归一化方法，将不同的合同所代表的资源和为项目所产生的效益以统一的数值来表示，其中c代表合同中的资源，value代表合同的效益，m1代表项目预期要投入的总成本，构建模型进行分析。

3.1 遗传算法建模

在使用遗传算法对合同选择进行优化的时候，使用基因对应每个待选合同，而基因值则代表合同签订所需投入的资源。

（1）初始化合同所消耗的资源c和所带来的效益value，数值如下（单位为万元）：

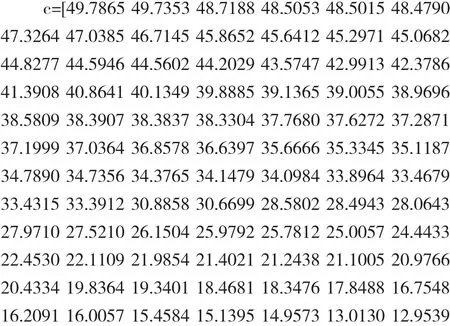
本文用g代表合同所耗费的项目资源及合同为项目所带来的效益的比值，得到g值如下：

设项目的预算总资源值为m1=1000万元。则目标如下：

第一，希望选出一组合同i1,i2,i3,…

（2）使用遗传算法＋贪婪算法修正对问题进行求解。

1）大型设备和课桌椅放置在一起不现实。若要真正实现学生技能训练，按照五人一组，40人一班计算，需要八套设备。设备以汽车为例，试想一下需要占据多大的空间？需要多大的教室？所以一些学校真实的做法就是摆上一套设备装装样子，实际使用率很低。

本文采用matlab编制目标函数文件，使用贪婪算法进行修正，贪婪算法的处理为：

（3）确定适应度函数：根据算法的特点，要将初始的目标函数换算为适应度函数，当函数值最小时，所获得的结果即为最优解。将适应度函数用目标函数值来表示，公式为：

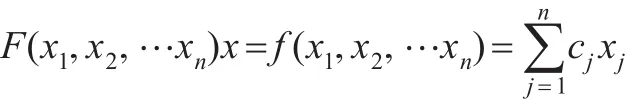
（4）初始化和参数设定。选择轮盘赌方法进行选择，并产生要配对的父代的序号，经过N次顺序调换，将原有顺序打乱，使相邻两个个体作为交叉的父代。

（5）变异，计算出适应度最大的合同和适应度最小的合同。本文选择的参数值是pc=0.5，pm=0.01。

3.2 仿真及结果分析

本文将参数按上述步骤输入Matlab程序进行仿真，选择种群大小150，代数500代，变异概率0.01为参数进行计算。程序运行耗时10.6秒。

随着种群进化，最佳合同组合的效益也在不断提高，演化轨迹如图1所示。

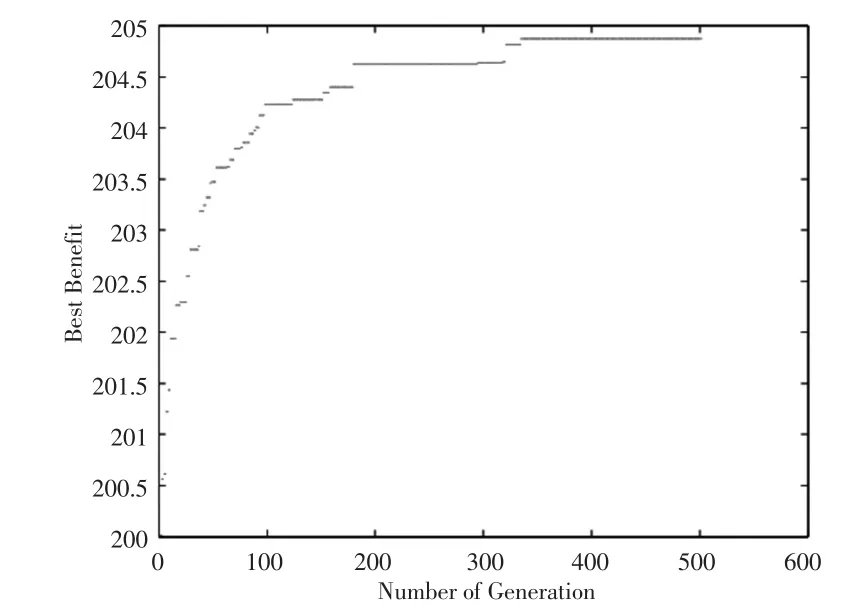
图1 最佳合同演化轨迹图

可以看出程序在330代之后开始收敛。得到结果如下，最优方案编码为：

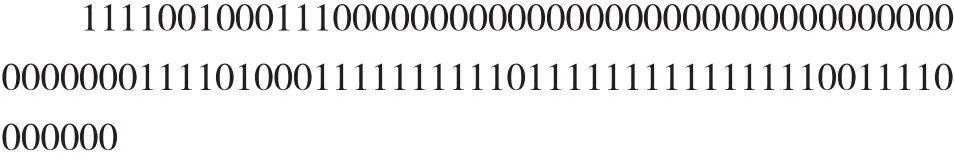
对应合同排列序号为：

（1）合同的成本和收益：

合同成本

合同收益

（2）总成本和总效益：

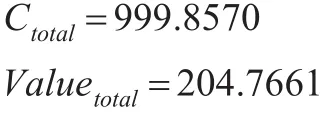
此时Ctotal非常接近我们总成本1000，说明此时资源利用率是最高的。表1列出了该项目优先选出的前25个合同。

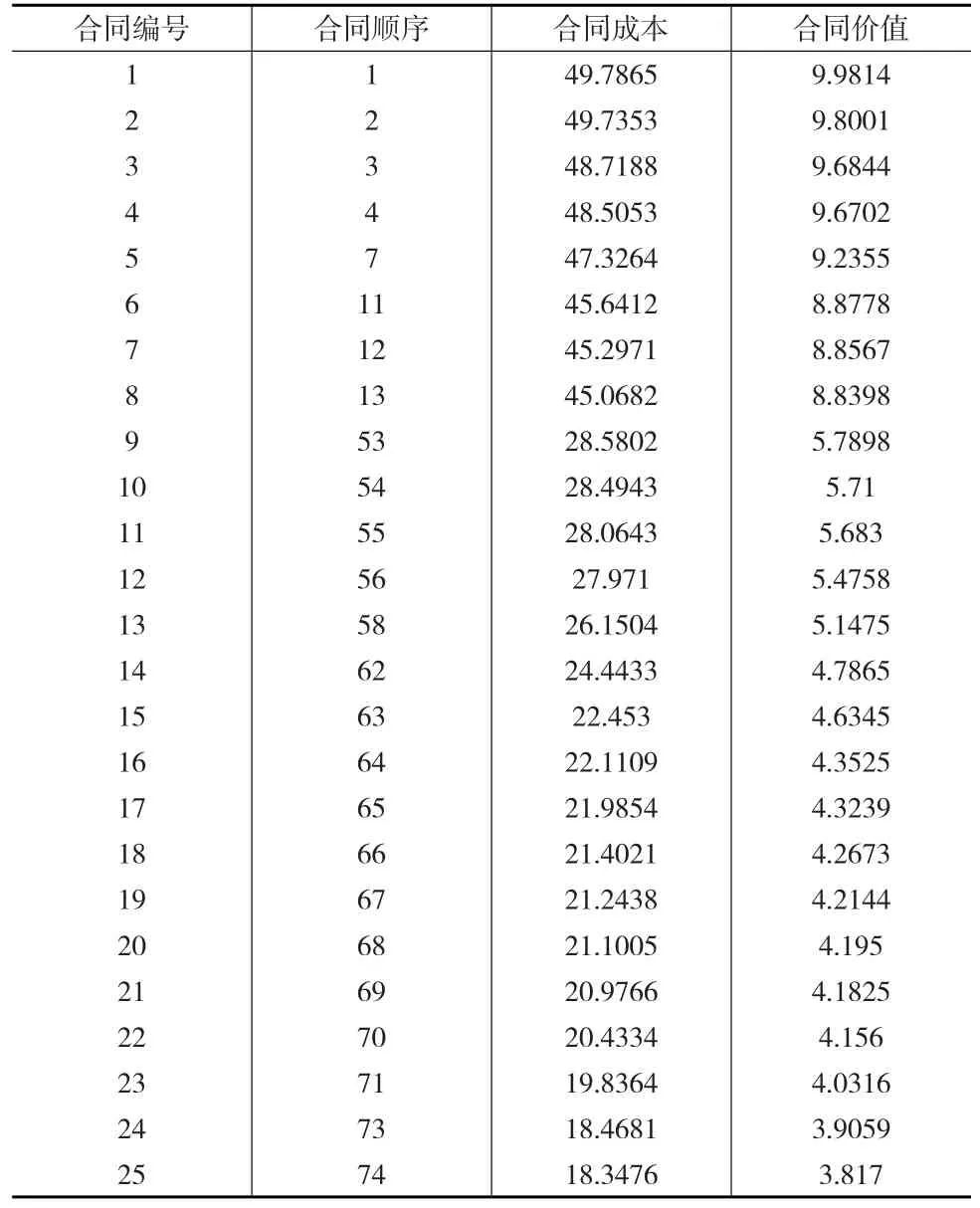
表1 前25个合同优化序列

4 结论

对于大型建筑工程项目，如何合适的选择合同进行签约，以及签约后如何排列履行合同的先后顺序，合同选择方案不同，会影响到整个项目最终实施，并对后续项目的成功完成和客户满意度提高具有重要意义。本文采用遗传算法特有的模拟技术，使用数学模型来模拟合同的优化选择策略，根据进化选择和基因遗传的原理，进行搜索设置，从而找到最合适的合同群组。遗传算法与神经网络技术及其他技术相比，具有所需的信息量少的优势，更适合应用于信息有限的合同前期。将遗传算法和贪婪算法结合，则可以避免选择局部最优的合同，从而得出整体的合同组合优化策略。该合同优化方法可以运用于大型工程项目尤其是海外大型项目的实际合同管理过程中，具有重要的实践意义。