死亡率变动相关性度量及其建模
2019-04-22王志刚张国庆
王志刚,张国庆,张 岩
(内蒙古财经大学 统计与数学学院,呼和浩特 010071)
1 Age-Period-Cohort死亡率模型
人口问题的研究是社会、政治、经济决策的基础,历来受到业界和学界的关注,其中死亡率预测模型作为人口预测的重要组成部分,一直是人口研究的重点。自1992年,Lee-Carter[1]提出第一个死亡率预测模型后,该领域产生了大量研究成果。这些模型由于主要考虑到了年龄(Age)、时期(Period)和出生年(Cohort)三个因素对死亡率的影响,因此这类模型被统称为APC模型。
APC模型的主要研究成果包括Lee和Carter(1992)[1]提出的Lee-Carter模型及其扩展模型,以及Cairns等(2006)[2]提出的CBD模型及其扩展模型。影响最为广泛的模型是Lee和Carter提出的Lee-Carter模型,具体表达式为:ln(mx,t)=αx+βxκt+εx,t,该模型包含了年龄和时间两个成分。Renshaw和Haberman(2006)[3]在Lee-Carter模型基础上增加了出生年因素得到相应扩展模型:ln(mx,t)=。Yang等(2010)[4]将Lee-Carter模型中的主成分项由一项扩展为两项,得到多年龄项和时期项的Lee-Carter扩展模型CBD模型及其扩展模型也体现了相似的特征,包括Cairns等提出的原始CBD模型,以及增加出生年项和扩展主成分项的扩展CBD模型。
经过二十多年的发展,APC模型积累了大量研究成果,不过这些成果主要集中在提高单一总体死亡率的拟合效果上。而在研究跨国、跨区域、多组别的死亡率风险时,构建能够定量描述多人群死亡率整体变动特征的多总体APC模型就变得必不可少,并有了一些有价值的研究成果[5、6]。此时细致考察多总体死亡率变动间的相关性,并以此为基础建立多总体APC模型就非常有意义。如果在死亡率变动过程中,不同总体死亡率变动轨迹不具有相关性,此时通过使用单总体死亡率模型,并进行简单加总就可以得到所需的结果,然而当死亡率变动过程中体现出相关性时,简单的加总会产生对风险估计的偏差,因此死亡率变动相关性的考察是建立多总体APC模型的前提。
2 相关性研究
现实经验告诉我们死亡率变动具有一定的相关性,为验证该经验,本文首先利用世界人口死亡率数据库(Human Mortality Database,简称HMD)中的死亡率数据,对世界范围内的死亡率变动过程中的共同趋势和相关性做出研究,本文选取HMD数据库中33个国家1985—2010年间的死亡率作为研究对象,观察60岁男性与女性死亡率变动趋势。结果表明,男性死亡率整体明显高于女性死亡率,且男性死亡率变化幅度略大于女性死亡率变化幅度。1985—2010年间,33个国家男性与女性死亡率变动均表现出相同的下降趋势,这表明33个国家的死亡率变动存在相关性。
虽然部分国家,如乌克兰等国受到原苏联社会动荡的影响,男性人口在2000年前后出现了死亡率上升的波动,但随着社会变动冲击逐渐减弱,此后这些国家很快再次进入死亡率下降趋势中;同时,这些国家的女性死亡率数据中体现出更强的同步性,这印证了死亡率逆向波动源于社会动荡的判断。
此外,文中利用HMD数据计算了不同国家间的相关系数,相关系数矩阵也验证了这一观点,绝大多数国家的死亡率相关系数都高于0.8。并且一些国家间,死亡率相关系数超过0.95。因此,本文认为世界死亡率变动具有广泛的、明显的相关性,该结论和实际生活经验相吻合,因此在模型建立过程中应该充分考虑相关性。
3 多元APE模型
3.1 研究回顾
针对死亡率模型变动过程中广泛存在的相关性,国外学者开始对现有单总体死亡率模型的研究成果做出改进,在死亡率建模中引入相关性,进而构建两总体以及多总体死亡率预测模型。为了将相关性纳入模型,国外学者针对单总体模型做了以下两种修改。学者首先尝试利用两者相关关系建立统一的死亡率估计模型对多总体死亡率进行整体估计。其中主要包括尝试使用线性回归对死亡率建模[5]和使用协整分析[6]对动态死亡率模型中的时间项进行建模。此外,Cairns等(2006)[2]针对一个总体及其子集总体,在假设子集总体的死亡率改善和总体死亡率改善间存在着一个固定比例关系的条件下,构建主人口和从属人口两总体死亡率模型。
这两种研究方案都是在原有动态死亡率模型上增加了新的假设条件,并基于此构建了多元动态死亡率模型。本文逐一考察这两个新增条件的合理性及其新增的约束。首先,在Yang等(2011)使用的回归关系[5]和Darkiewicz等(2004)使用的协整分析[6]中,两种方法都要建立回归模型,而回归分析通常是将因变量的变动看作为自变量变动的结果。本文认为不同地区或不同组别的死亡率变动都是由自身所处的经济、社会及生物学特征所决定的,而不是由另外一个人口总体死亡率变动轨迹所决定的。因此,使用回归方法对死亡率变动进行建模,相当于对死亡率变动过程中外加了一个没有被验证的,并且很可能是错误的外加条件。本文认为,死亡率改善进程中体现出的相关关系,应该是社会、医疗和经济条件共同影响下的结果,虽具有相关性,但彼此之间不一定具有因果关系,所以本文认为在没有被验证之前,应该使用相关模型,而不是回归模型描述两者相关关系。
同时在使用协整分析工具时,针对两变量和多变量使用的模型和处理难度具有明显的差异,特别是多变量协整分析中使用的Johanson协整分析和VECM工具,需要针对不同数据进行有针对性的建模,模型使用者要在其中进行大量的参数选择和模型设定,难度明显高于两变量的Engle-Granger协整方法和ECM工具,对模型使用者提出较高要求,不利于相关方法的广泛普及。
在Cairns等(2011)构建主人口和从属人口两总体死亡率模型中要求大总体死亡率m1(x,t)和子集总体死亡率m2(x,t)的比保持不变,即要求C为常数。这无疑也增加了一个比较苛刻的前提假设。这也是Cairns将其模型使用范围限定在一个总体是另外一个总体的子集的原因。即使在Cairns限定的条件内,该假设也是一个无法验证的假设。
另一点值得说明的是,虽然这些方法使用了不同的假设去构建多总体动态死亡率模型,但这些模型的基础——单总体动态死亡率模型,不是选用原生的Lee-Carter模型,就是选用Lee-Carter扩展模型(包括CBD模型研究团队中的Cairns在构建多元死亡率模型时,也使用了Lee-Carter扩展模型),因此这样看来,现阶段多总体动态死亡率模型构建中的基础模型都选用的是数据拟合效果较好、应用较为广泛的Lee-Carter模型族。
3.2 相关性分解
与已有的多总体死亡率模型构建思路不同,本文不引入任何新建假设条件将相关性一揽子纳入模型中,而是从APC动态死亡率模型构成因素(年龄、时间、出生年)入手,探寻这些因素对死亡率变动的影响,并进而将相关性纳入到动态死亡率模型中,构建出多总体动态死亡率模型。模型选取带出生年因素Lee-Carter扩展模型:
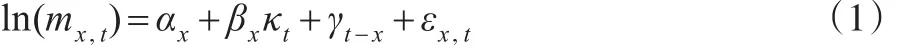
为了通过模型分解不同因素随死亡率变动体现出的相关性,本文从HMD数据库中选取了数据质量较好,分属于三个不同大洲的澳大利亚、美国和日本三个国家作为示例。使用SVD方法分别针对三个国家的参数做出估计,并将估计结果绘制为折线图(见图1)。图形显示这些国家在两个年龄项和一个时期项上存在着明显的相关性,而同时在出生年项上并不具有明显的相关性,同时使用统计相关性检验也支持该结论。据此,通过对数据的分析可以看出,死亡率变动过程的相关性主要体现在两个年龄项和一个时间项上,据此构建相应的多元APC模型。
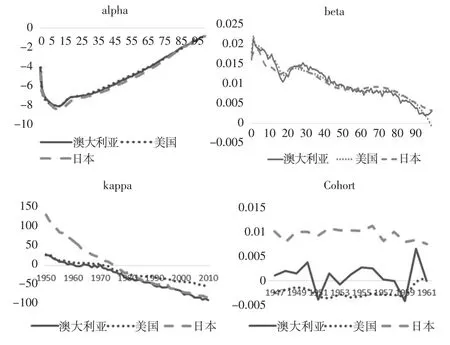
图1 澳大利亚、美国和日本三国Alpha、beta、kappa、cohort折线图
出生年因素主要体现了在死亡率变动过程中一代人具有与其他不同出生年人群,在死亡率上体现出的特有特征,会在残差热点图中体现出明显的积聚和规律性变动。文中给出美国人口残差热点图(见下页图2),图中显示残差分布并不是白噪声,而是具有明显的规律性。这种规律性也体现在澳大利亚和日本两个国家死亡率残差图中(图略)。因此,有必要在模型中增加出生年因素项,这也是本文没有选择原生Lee-Carter模型,而是选用增加出生年因素项的扩展Lee-Carter模型的原因。

图2 美国人口数据残差热点图①图中使用了单色配色方案,颜色深浅主要体现出残差绝对值的变动趋势。实际问题中队列效应带来的残差具有持续性,不会在正负之间大幅波动,单色图也可以观测到变动趋势。可以联系作者索取彩色图。
3.3 多元APC模型
对于k个组别,多元的APC模型中只需要考虑年龄和时期两个方面的相关性,对于出生年项不需要考虑其相关性对整体模型的影响。其中第一部分年龄项包括评价死亡率水平和死亡率改善系数,这两个非参数估计值不具有外推性,同时相关性内置在了估计值中,因此非参数项和包括了死亡率随年龄变动中体现出的相关性特征,相应的多元形态为:

在现有研究成果中,第二部分时间项通常项设定带漂移项ARIMA(0,1,1)②虽然此处限定了kt项的具体表达式,但是后面的研究框架并不限于该情形,可以推广到其他情形。的时间序列,即:

其中,i=1,2,...,k,本文将其相关性内置到时间序列产生机制的中,将et服从一元正态分布的假设扩展至多元正态分布:
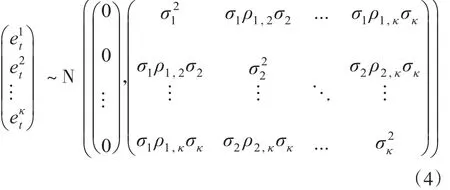
至此,式(2)至式(4)构成包含不同组别死亡率变动相关性的多元APC模型。
3.4 应用
假设目标人群是一组由澳大利亚、美国和日本三个国家女性人口1:1:1混合构成,并且其死亡率变动特征与本国人口变动特征相同。在2010年,该人群加入一个为期30年的社会保障计划,这组人群在该计划内的平均停留时间及其分布可以使用上文介绍的方法加以估计。
根据前文的分析可知,三组人群的死亡率随年龄波动具有相近特征,同时死亡率改善具有相似的轨迹,其中死亡率改善的相关系数矩阵分别为ρAU,USA=0.99,ρAU,JPN=0.96,ρUSA,JPN=0.98都是高度线性相关,再一次印证了使用多总体APC模型建模的必要性,相应的的分布为,使用随机模拟的方法产生10000组样本,基于模拟结果得到对未来该人群在计划内的平均时间为14.42年,密度函数估计结果见图2,为了和现有方案作比较,本文还计算了不考虑相关性情况下的平均时间为14.43年,两种方法计算结果比较接近,差异主要源于样本偏差和计算误差。但两种估计得到的方差估计结果和密度函数明显不同(见图3)。本文的方法考虑了不同总体间变动的相关性和死亡率变动的同步性,这种相关性会增加整个人群死亡率波动的方差,多总体APC模型考虑了这种相关性得到的密度估计函数方差更大,而独立估计因忽略相关性,会低估方差。
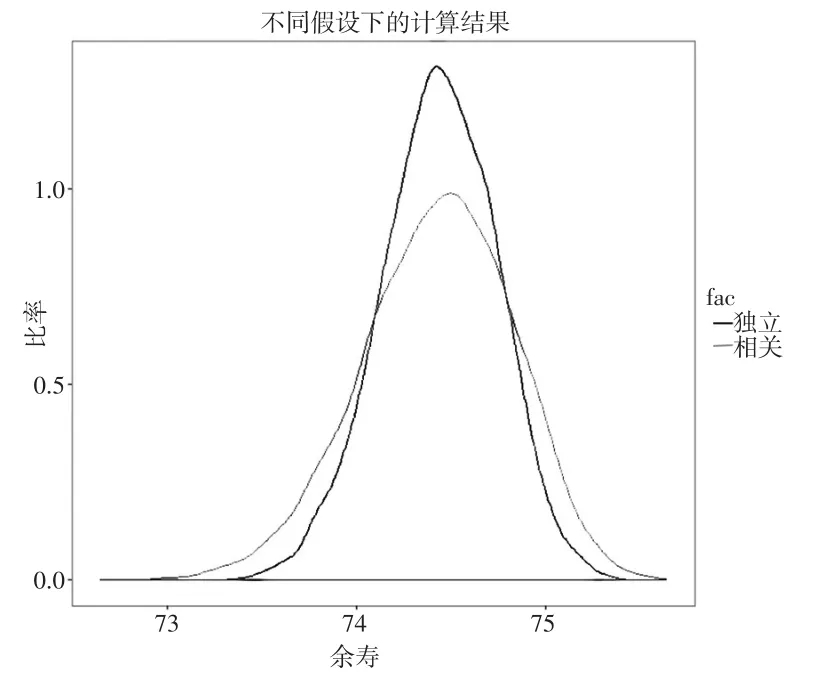
图3 两种方法估计对比图
4 结论
本文以死亡率变动的相关性为切入点,利用1985—2010年澳大利亚、美国、日本历史死亡率数据,基于带有出生年因素项的lee-carter扩展模型,建立了多总体APC模型,定量研究显示:三个国家在两个年龄项和一个时期项上存在着明显的相关性,在出生年项上并不存在明显的相关性;此外,充分考虑死亡率变动过程中相关性的多总体APC模型更加准确地展示了余寿的波动范围,更符合实际情况。
为了将全球化背景下,死亡率变动具有相同的趋势,纳入到模型中,文中使用了澳大利亚、美国、日本三个分属于不同大洲的国家,出于篇幅考虑,没有将研究扩展到所有国家,但本文的研究框架可以适用于更多国家间死亡率研究,具有借鉴价值。
本文建立的多总体APC模型是对传统APC模型的扩展,是长寿风险管理等相关问题的基础,将为长寿风险的识别和量化、年金产品的定价、养老产品的设计、个体退休计划的制订、养老保障体系的完善等提供重要参考。
