隐马尔可夫多元线性回归模型及其贝叶斯估计

刘鹤飞

（曲靖师范学院 数学与统计学院，云南 曲靖 655011）

0 引言

回归模型是最经典的统计学模型，其广泛应用于经济学、管理学、心理学、教育学、医学等领域。从最简单的一元线性回归到多元线性回归，再到非线性回归、广义线性回归，众多研究者对回归模型进行了深入的研究、探索和各种改进。

隐马尔可夫模型是一种基于随机过程的统计模型。近年来，隐马尔可夫模型在各个领域都得到了广泛的应用和发展。在经济管理领域，利用隐马尔可夫模型处理异质面板数据，在生物医学领域，利用隐马尔可夫模型对DNA序列的分布进行推断[1]；在人工智能领域，利用隐马尔可夫模型进行语音识别[2]、图像处理等。

隐马尔可夫模型是由两个随机过程构成[3]。一个是状态转移序列，它是一条单纯的马尔可夫链，另一条是与状态对应的观测序列。在实际问题中，我们只能看到观测变量的集合，无法看到观测状态序列的集合。隐马尔可夫模型的研究内容就是根据可观测的序列集合去推断不可观测的状态转移特征以及每个状态下的分布信息[4]。

本文将隐马尔可夫模型与回归模型相结合，提出隐马尔可夫回归模型的概念。这种模型在许多领域都有实际的应用，例如，在经济领域，由于股票指数与经济增速、CPI指数、银行利率等指标都有线性相关关系，并且可以建立这几个自变量与因变量（股票价格指数）之间的多元线性回归模型。但是，股票市场处于牛市和熊市的不同状态时，因变量和自变量之间的回归关系是不同的。此外，不同状态之间也是可以相互转化的，研究者还想了解不同的状态之间相互转化的关系。隐马尔可夫多元线性回归模型就是研究不同状态之间的相互转化规律以及每个状态下因变量和自变量之间回归关系的模型。

本文将以多元线性回归模型为例，详细介绍隐马尔可夫多元线性回归模型的数学定义，推导用贝叶斯方法对模型的参数进行估计的理论过程。最后利用MCMC算法模拟参数的后验，用后验均值作为参数的估计值，并与模型参数的真值进行比较，检验该方法估计的可靠性。

1 模型描述

假设隐状态的转移过程满足以下马尔可夫链的条件：

其中u=1，2，…，K；s=1，2，…，K；t=2，3，…，T。

这里，aus是从前一个时间点的隐状态u向后一个时间点的隐状态s的转移概率。我们称所有可能的隐状态转移概率构成的矩阵为隐状态转移概率矩阵，记为：

在给定隐状态的条件下，描述自变量与因变量关系的多元线性回归模型定义为：

其中，β是P维回归系数向量，εk是模型的误差，且：

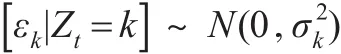
2 贝叶斯推断原理

将隐状态转移概率矩阵记为A；将多元线性回归模型中的参数(βk，)记为θ；将隐状态向量记为Z。则该模型的贝叶斯推断问题为，其中D=(Y，X)。

马尔可夫链蒙特卡洛算法模拟过程的具体步骤如下：

（1）更新隐状态Z；

（2）更新潜变量A；

（3）更新模型参数θ。

其中，更新模型参数θ又可以分为两小步：

（1）更新正态分布的方差；

（2）更新多元线性回归系数βk。

每一步更新参数，都是借助于Gibbs抽样[6]和MH算法[7]。这需要对每个参数设定其先验分布，并推导出后验分布。

3 先验分布

贝叶斯理论认为，每一个参数都是一个随机变量[8]。因此，在进行贝叶斯推断时，必须事先为每一个参数都选择一个合适的先验分布。Robert[9]在研究隐马尔可夫正态模型时，选择对称的狄尼克莱分布作为转移概率矩阵每一行的先验分布。Minka[10]在研究线性回归模型参数的贝叶斯估计时，选择多元正态分布和倒伽玛分布作为线性回归模型参数的先验分布。借鉴以上经验，本文为模型中所有参数选择的先验分布如下：

其中，Ak表示转移概率矩阵的第k行，D表示狄尼克莱分布，α是狄尼克莱分布的超参数；μ0k，Λ0k是多元正态分布中的超参数，Inv-Gamma表示倒伽玛分布，是倒伽玛分布中的超参数。

4 后验推断

贝叶斯后验推断的主要任务是利用样本的观测信息和参数的先验信息推导出参数的后验信息[11]。对于本文的隐马尔可夫多元线性回归模型来说，即也就是要根据观测变量集合和模型参数的先验分布去推断模型的隐状态、概率转移矩阵、多元回归模型的参数。其中，转移概率矩阵A、多元回归模型的系数β是隐马尔可夫多元线性回归模型中的参数，是需要进行估计的对象。由于这个分布的复杂性，本文使用了MCMC方法来进行后验模拟，用后验均值作为相关参数的估计。这就需要相关参数的全条件后验分布。

其中，πk是在转移概率矩阵A的作用下，隐状态达到稳定时，隐状态k的稳定概率；是观测变量在隐状态k下的似然函数。

下面推导在隐状态确定的条件下，多元线性回归模型参数(βk，)的全条件后验分布。

记所有隐状态为k的观测数据集合为Dk，所有隐状态为k的因变量集合记为Yk，所有隐状态为k的自变量的集合为Xk。

在此记法下，Yk的似然函数可以表示为：

根据条件概率的计算公式可得：

于是，可以把参数(βk，的后验分布看成一个多元正态分布和一个倒伽玛分布的乘积，它的具体形式为：

为简单起见，可将该后验分布看成如下两部分：

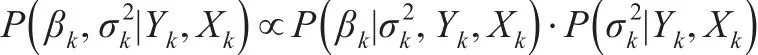
则βk和这两个参数的后验分布分别为N，即参数为μn和的多元正态分布和参数为an和bn的倒伽玛分布。其中：

5 实证模拟

为了检验上文所推导的模型参数的贝叶斯估计方法，这里将事先给定模型参数A和θ的真实值。根据概率转移矩阵A生成一个隐状态序列集合，再根据每个观测点的隐状态取值和对应于该隐状态的多元线性模型参数的值，生成每一个观测时间点的观测向量。然后利用所有的观测变量集合，根据所推导的后验分布，用MCMC算法对模型的参数进行后验模拟。取后验均值作为模型中参数的估计值。最后将参数的贝叶斯估计结果与事先给定的真实值进行比较，观察估计的效果。

取隐状态的个数K=2，则隐状态的概率转移矩阵是一个二阶方阵，令：

设每个隐状态下的多元线性回归模型都有3个自变量，具体为：

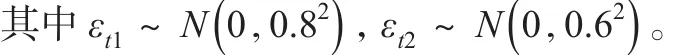
模型中，取观测时间点总数T=200，则生成的观测变量集合是一个4×200的二维数组。先验分布中超参数的取值分别为：，其中I3表示三阶单位矩阵

使用MCMC算法进行后验模拟时，取迭代总次数为5000，去掉前面3000次的迭代结果，用后面2000次的后验均值作为参数的估计。各参数的真实值与估计值如表1所示。

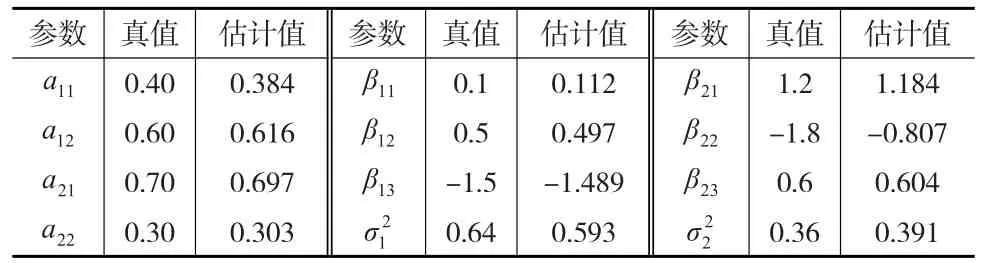
表1 模型参数的真值与估计值

6 结论

本文介绍了隐马尔可夫线性回归模型，推导了隐马尔可夫多元线性回归模型参数的贝叶斯估计方法。并且通过实证模拟，将模型参数的贝叶斯估计结果与事先设定的模型参数的真实值进行比较，发现估计效果良好，这说明本文给出的模型参数的贝叶斯估计方法是可靠的。可以用隐马尔可夫多元线性回归模型来研究含有多个状态的自变量与因变量的关系模型，分析不同状态之间的转化关系，以及每个状态下多个自变量与因变量之间的线性回归关系。

本文仅以简单的多元线性回归模型为例介绍了隐马尔可夫线性回归模型，未来还可以研究隐马尔可夫非线性回归模型等更复杂的模型。此外，还可以研究隐状态个数未知情形下的隐马尔可夫回归模型，利用贝叶斯因子、可逆跳跃MCMC算法等方法对隐状态个数进行模型选择。