船舶锚泊系统分析

柳 辉，崔 杰，邓小康，陈 琅

（江苏科技大学 船舶与海洋工程学院，江苏镇江 212003）

0 引言

21世纪以来，随着经济全球化进程的不断推进，各国之间的贸易往来日趋频繁，海运成为主要的运输方式。但是，船舶在停泊或遭遇恶劣海况时不可避免地会受到风、浪、流载荷的共同作用，从而产生复杂的多自由度耦合运动。因此，为了保证船舶能够安全运营，其锚泊系统至关重要。

JOHANSSON[1]于1976年在他的博士论文中建立了锚泊系统的有限元模型，并且对其动力响应进行了分析。他不仅考虑到锚泊系统与阻尼有关的速度、锚链张力的突变，还考虑到了锚泊系统偏离平衡位置的位移，且它的有限元模型为非线性模型。由此他对有限元模型的时域进行了研究，得出的数据可以用来分析锚链在某一瞬时的状态下的具体情况。JOHANSSON在前人的基础上，创造性地提出了一种新计算方法，用来求解耦合运动方程的数值积分。随后，GOBAT等[2]提出了一种新的经验模型，用于计算由于悬链线型锚链上端受到垂向运动引起的动张力。这种新的经验模型可以很好地适用于海洋波频作用力，而且还可以用来计算锚链张力的标准方差。将模型的计算结果和一系列海况下测量到的实际海洋锚链结果进行比较，两者之间最大的误差在 8%～11%之间，标准方差的误差则在 2%～3%之间。研究结果表明：当水平运动产生显著变化时，具有最大平均张力和动张力的地方最易产生最大误差。SHASHINKALA等[3]在前人的研究基础上，采用有限元方法研究了波浪对单点系泊驳船干扰的三维问题。他们通过对比有限元方法得出的数值和在不规则波及规则波状况下得到的模型试验数据，得出了不同系泊点驳船的响应与锚链刚度系数之间的关系。无论在规则波情况下，还是在不规则波情况下，分析结果和试验数据都基本一致。BINGHAM[4]利用一种三维方法来求解船舶的运动响应；INOUE等[5-7]考虑了非线性的影响，并对系泊系统的水动力相互作用进行分析；OHKUSHU[8]利用二维理论探索了浮体间的相互影响；KORDAN[9]提出一种用来模拟斜浪作用下结构间耦合分析的理论；CHOI等[10]利用高阶边界元法分析2个结构之间的相互作用。范菊等人[11]采用二阶频域摄动理论来探讨转塔式锚泊储油轮的动力响应，对转塔式锚泊储油轮在压载状态下的一阶运动、二阶运动的响应谱和锚泊线张力谱进行计算，通过将计算所得的数据与相应的模型试验数据进行对比，发现理论结果与试验数据基本一致，由此得出二阶频域摄动理论可运用于转塔式系泊储油轮动力响应分析的结论。FAN等[12]采用频域方法研究了波频运动引起低频慢荡阻尼力问题中锚链所引起的力。实质上，锚链所造成的阻尼与其运动间的初相位是密不可分的。因此可以通过频域分析得出相位信息，再采用摄动理论推导得出二阶的锚链张力响应函数，最后对比算例和相应的时域结果，事实证明，算例所得结果与时域方法所得的结果基本一致。

本论文根据实际工程的需要，使用ANSYS软件对120.1 m沿海散货船建立锚地系泊的有限元模型，在典型工况下对该船舶锚地系泊进行数值模拟，并对锚链张力进行校核、对运动响应进行分析。

1 数值模型

1.1 散货船有限元模型

本文计算所需的120.1 m沿海散货船的主要参数见表1。本文使用ANSYS软件进行建模，由于主要计算在风、浪、流载荷共同作用下船舶锚泊系统的锚链张力及其对运动的响应，因此只需建立该船的外表面模型即可。由于船舶左右对称，故只需建立一半的模型，再利用对称的方法分析即可。图1为该散货船的网格划分图。

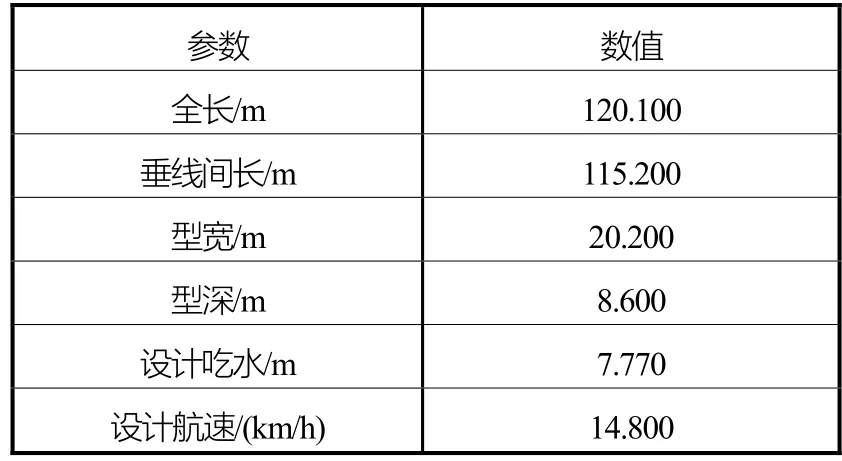
表1 120.1 m沿海散货船主要参数

1.2 锚泊系统有限元模型建立

根据船舶的主尺度和相关规定，最终选用链径为56 mm的锚链，表2为该锚链的主要参数。

表2 锚链主要参数

在建立锚泊系统有限元模型之前，还需要做的工作就是估算导缆孔的位置和海底系泊点的位置。根据船舶的型线图和所选锚链长度，可以很容易地估算出导缆孔与海底系泊点的位置。估算完成后，就需要编写DAT文件以设置导缆孔和海底系泊点的位置。完成导缆孔位置和海底系泊点位置的设定后，还需将导缆孔和海底系泊点用锚链连接起来。最后，只需将改好后的DAT文件导入AQWA软件中计算即可。至此，整个有限元模型建立完毕，如图2所示。

图1 120.1 m沿海散货船网格划分图

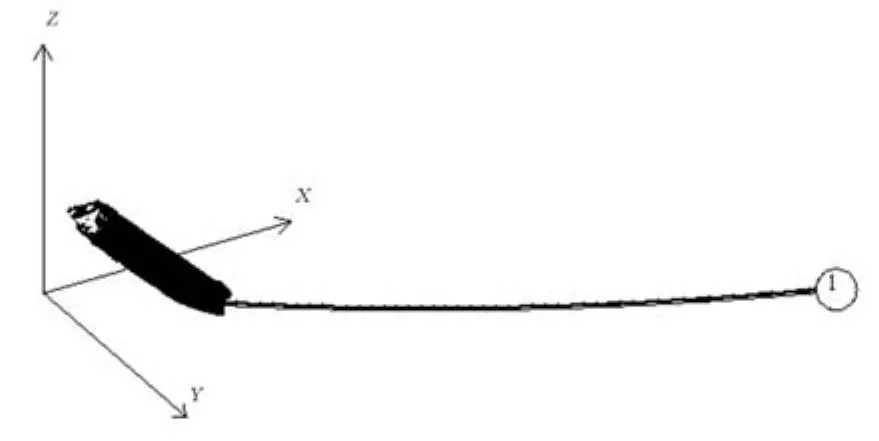
图2 船舶有限元模型

2 锚泊系统计算分析

2.1 环境载荷

为了弄清船舶锚泊系统随风、浪、流载荷的运动情况，遂选取了以下3种工况，分别为：一年一遇（工况1）、五年一遇（工况2）和十年一遇（工况3）。该3种工况对应的参数见表3。本论文中将水深设为 100 m，波浪方向、风向和流向均设为-180°。

表3 3种工况的参数表

2.2 船舶锚泊系统运动响应分析

在风、浪、流载荷共同作用于船舶的基础上，对锚泊系统进行模拟分析，便可得到船舶在六个自由度方向上重心随时间的变化曲线。本文通过计算，分别得出了在工况1、工况2、工况3下锚泊系统运动响应的时间历程曲线。由于篇幅有限，现给出工况3下锚泊系统运动响应的时间历程曲线图，如图3～图8所示。

3个工况下船舶在六个自由度上的中心变化曲线的走势基本一致，只是数值大小不同，因此，选择工况3为代表进行详细解释。

工况3下船舶纵荡时历曲线在极短的时间内急剧下降，最后在20 m附近上下震荡；船舶横荡时历曲线则随着时间的推移先增大后减小，最终达到稳定状态；船舶垂荡时历曲线在开始后的极短时间内剧烈震荡，振幅较大，随后振幅减小，但始终保持平衡；船舶横摇时历曲线与船舶垂荡时历曲线有所相似，也是在开始后的极短时间内剧烈震荡，振幅较大，而后振幅明显减小，基本为 0；船舶纵摇时历曲线则一直保持剧烈震动的趋势；船舶艏摇时历曲线最为平缓，随着时间的推移逐渐下降，直至趋于稳定。在工况3下，船舶重心在六个自由度上均有剧烈变化，但仍符合安全要求。

图3 工况3下船舶纵荡时历曲线

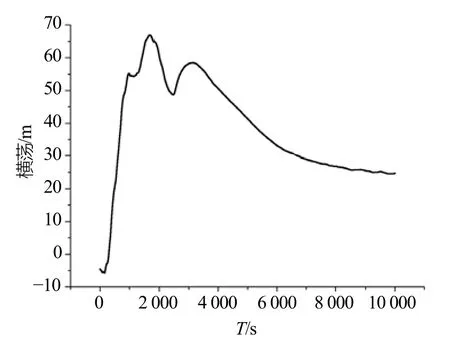
图4 工况3下船舶横荡时历曲线

图5 工况3下船舶垂荡时历曲线

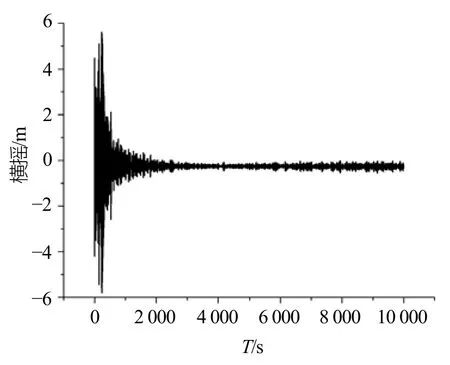
图6 工况3下船舶横摇时历曲线

图7 工况3下船舶纵摇时历曲线

图8 工况3下船舶艏摇时历曲线

2.3 船舶锚泊系统锚链张力校核

锚链张力校核是船舶锚泊系统设计中最为关键的工作，锚链张力的大小、所受张力是否超出锚链破断载荷以及锚链所能承受的最恶劣海况等都是与船舶和船员安全息息相关的重大问题，也是本论文最为重要的一节。图9～图11分别给出了在工况1、工况2、工况3下锚链张力的时间历程曲线。

图9 工况1下船舶锚链张力时历曲线

图10 工况2下船舶锚链张力时历曲线

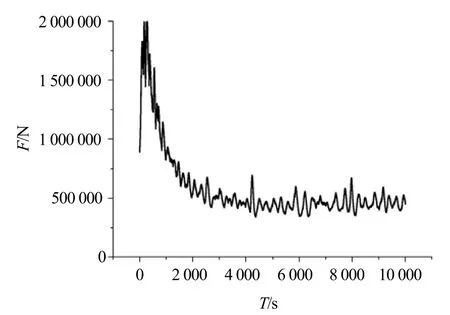
图11 工况3下船舶锚链张力时历曲线

从图9～图11可看出：在不同工况下，船舶锚链张力随时间的走势是基本相同的，都是在刚开始加载的时间里，船舶锚链突然受到一个较大的张力，随着时间的推移，锚链所受张力会慢慢减小，最终达到动态平衡。所选锚链的链径为56 mm，破断载荷为2 430 kN。

从图9可看出：锚链所受最大张力只有1 068 kN，破断载荷与锚链最大张力之比为2.275，证明了此锚链完全可以满足船舶在一年一遇海况中的使用要求。

从图10可看出：锚链所受最大张力为1 645 kN，破断载荷与锚链最大张力之比为1.477，同时也可证明此锚链满足船舶在五年一遇海况中的使用要求。

从图11可看出：锚链所受最大张力为1 957 kN，破断载荷与锚链最大张力之比为1.242，虽然锚链所受最大张力仍小于锚链的破断载荷，但是富余较少，容易出现意外。由于所选船舶为沿海散货船，实际遇到的海况相对于校核的海况来说等级较低，所以也能够满足使用要求。

为了校核锚链张力，本章利用 AQWA有限元软件对船舶所在工况进行设定，所选工况分别为一年一遇、五年一遇和十年一遇，最终得到了在六个自由度上船舶重心和锚链所受张力随时间的变化情况。在六个自由度上，船舶重心的偏移程度都在允许范围之内，同时锚链所受张力也小于锚链的破断负荷且有富余。加之本船为沿海散货船，沿海实际海况对比深海海况较为缓和，因此，所选锚链满足安全和生产的要求。

3 结论

本论文以 120.1 m沿海散货船为原型，在ANSYS-AQWA中建立了船舶及其锚泊系统的有限元模型，并对有限元模型进行了锚泊系统运动响应分析和锚链张力校核。通过对该船舶的3个典型工况的分析和校核，结合数值模拟得出结论。

从船舶锚泊系统的锚链张力校核部分可以看出，无论在哪种工况下，锚链所受张力的变化趋势基本一致，在极短时间内，锚链所受张力以一较大值开始急速上升，达到最大值后又开始下降，直至趋于动态平衡。锚链在这3种工况下所受张力的最大值均低于锚链的破断载荷且有富余，均能满足相应的安全度要求。本文数值模拟的结果可以为同等类型的船舶锚泊系统提供借鉴与参考。