浅水条件下15万吨级FPSO波浪载荷与运动预报分析

韩 熠，杨 辉，刘 波，杨 亮，方 堃

（海洋石油工程股份有限公司，天津 300451）

0 引言

作为海上油田的生产储油设备，大型浮式生产储油卸油装置（Floating Production Storage and Offloading，FPSO）长期连续作业于固定海域，虽然多数FPSO采用船型结构，但由于不解脱不定期进坞的要求使得FPSO的船体强度和疲劳强度都比一般船舶的标准更高。因此，在前期设计阶段中，需对FPSO整个生命周期内可能受到的波浪诱导弯矩、剪力以及运动参数做出可靠预报。

当FPSO系泊在一个浅水海域，浮体的吃水与水深相对接近，此时既要保持大的装载能力，又要具有良好的运动性能以保证海上作业安全，因此，问题更加复杂化。近年来，人们对浅水大型浮式结构的研究愈发深入，贺五洲等[1]、杨玥等[2]曾提出，对于中等以上水深，FPSO的响应主要取决于风、浪、流及其系泊系统，与水深关系并不大，但是对于浅水而言，水深效应逐渐明显。随着水池试验的发展，谢永和等[3]通过试验数据证明当水深变浅时，垂荡和纵摇的响应峰值变小，弯矩和剪力则会增大，而且水深越浅波浪诱导垂向弯矩与剪力的增幅越明显。由此可见，浅水效应在实际工程应用中会对结构优化产生影响。而对于浅水油田前期开发方案的选取，在快速筛选设计工况及选定设计载荷的过程中，有以下问题值得关注：1）浅水条件下不同装载情况载荷预报的差异；2）使载荷响应达到最大的环境条件是什么；3）由于浅水效应的存在，钢制海船入籍规范所推荐的载荷规范值是否依然保守；4）浅水效应对结构设计而言会带来哪些关注点。

为探讨以上问题，笔者以渤海海域大型 FPSO为例，计算其在不同压载情况下的RAO（Response Amplitude Operator，反应量），并基于渤海环境条件统计响应极值，并与挪威船级社规范（DNV GL）推荐值进行比较以探究相关研究结论。

1 浅水规则波船体载荷计算理论

规则波中的三维源汇理论假设船体运动及波浪均是微幅、线性的，流体视为无粘性的理想流体，则船体的运动方程为

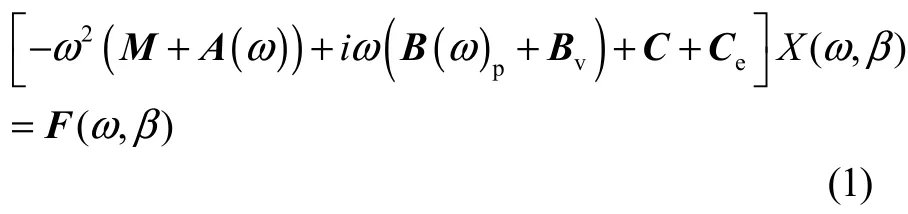
式中：ω为圆频率；β为浪向角；M为广义质量矩阵；A(ω)为附加质量阵；B(ω)p为势流阻尼阵；Bv是线性粘性阻尼阵；C为静水回复力矩阵；Ce为外部回复力矩阵（锚链力等）；F(ω,β)为波浪激励力矩阵[4]。

计算结构响应首先要计算波浪力F(ω,β)，常用势流理论的方法，速度势可线性分解为3部分，入射势、绕射势及物体自身运动产生的辐射势。速度势在流场中满足拉普拉斯方程及4类边界条件（定解条件）：自由表面条件、物体湿表面条件、海底条件及辐射条件（无穷远处边界条件），再用伯努利方程计算物体湿表面压强。求解速度势常用格林函数法[2]。船舶在浅水中受力状况有所改变，数值解析主要体现在有限水深的格林函数积分表达式为奇异二重积分，这样当水深与船舶吃水的比值小于一定值时，船舶的水动力系数及所受波浪扰动力等与深水情况有所不同。一般认为，当水深小于4倍吃水时就会出现浅水效应，而小于2倍吃水时将发生很大差异。主要表现有：平面漂移运动加大、垂直及横向摇摆运动减缓等[5]。

2 波浪载荷和运动预报的基本理论

用无数个规则波相互叠加生成不规则波，比较符合真实海面上的波浪，此时应采用概率和随机理论的方法计算波浪诱导船体运动和波浪载荷。本文将采用短期统计的方法预报100年一遇环境条件下的极值响应。

首先应求出船体在规则波中的传递函数，然后通过实际海域的波浪谱计算船体运动和载荷的响应谱[6]。预报方法分为短期预报和长期预报。短期预报是在假设海况条件不变的数小时内船体的响应值。大量事实数据表明，船体运动和载荷的短期响应服从瑞利分布。

短期海况通常用波浪谱来表示其特性，海浪谱密度函数S(ω)是平稳随机过程的频率描述，反应了不规则波内各单元谐波的能量分布情况。短期预报的波浪幅值及波浪诱导船体运动幅值、载荷幅值、应力幅值符合瑞利分布，其概率密度函数为

概率累计函数为

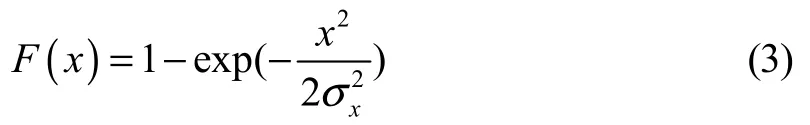
三一有义值、百一平均值等响应值均是在一定超越概率下得到的统计值。

3 波浪载荷和运动分析预报

本文研究对象是渤海油田15万吨级大型船型生产储油系统，该大型FPSO总长L=276 m，型宽B=51 m，型深D=23.6 m，满载排水量Δ=199 959.9 t，满载吃水T=15.66 m，空载排水量Δ=118 705.4 t，空载吃水T=9.45 m，方形系数Cb=0.93。

在DNV GL的SESAM软件中进行模拟时，使用前处理模块GENIE建立FPSO水动力湿表面模型和质量模型，见图1和图2；用WADAM模块计算船体运动和波浪载荷的传递函数[6-8]。

图1 湿表面结构

图2 质量模型示例

3.1 水动力模型

设定该FPSO将服役于渤海海域，工作水深只有22 m，水深吃水比仅为1.41，水动力模型全部由三角形和四边形单元组成。全船共有7 414个单元和7 728个节点。

用质量棒来模拟整船质量分布，可以得到截面载荷的分布。FPSO的总重量可分为空船重量和装载重量，将空船重量保持一致，装载重量根据装载手册进行调整，使得惯性半径与重量资料数据一致，可分别得到满载和压载工况下的质量模型。

3.2 坐标系定义

为了定义和计算浅水超大型FPSO的运动和波浪诱导载荷响应，本文建立了浅水大型FPSO的整体坐标系，见图3。整体坐标系原点位于FPSO基线的中心处，x轴正方形从船尾指向船首，y轴正向指向左舷，z轴向上为正。整体坐标系用于描述入射波的方向和入射波的速度势。

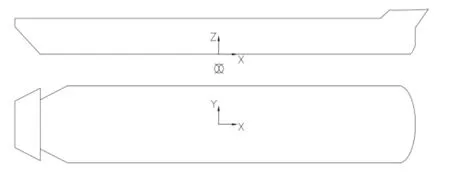
图3 参考坐标

3.3 装载工况

为得到船体运动和载荷的预报极值，分别考虑船体满载和空载两种装载状态，见表1。

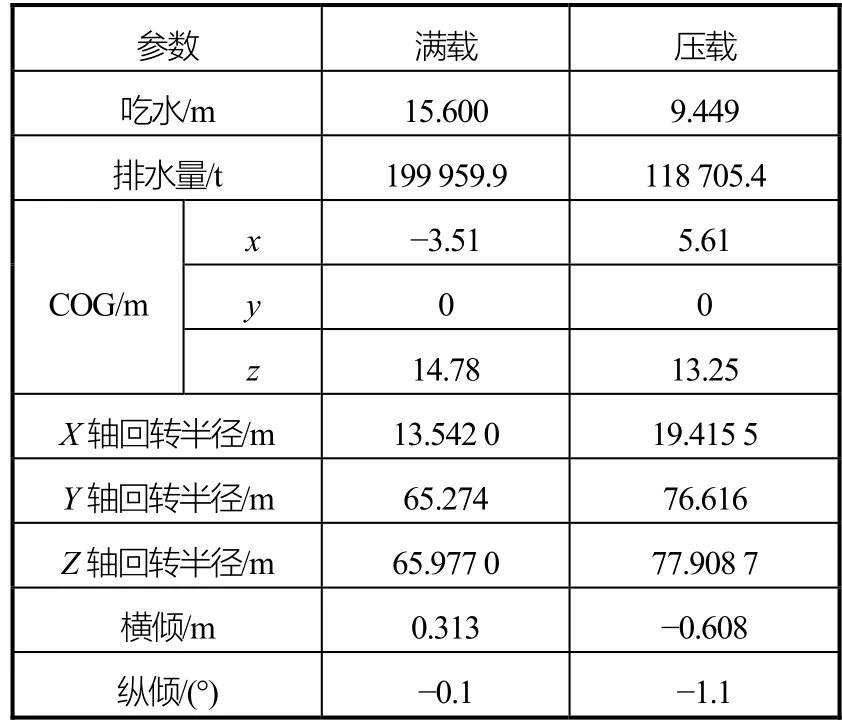
表1 装载工况

3.4 传递函数及响应统计

为研究浅水大型FPSO在特定水深下波浪诱导载荷响应随浪向变化的规律，选取0°～180°共13个浪向角，以15°为间隔。波浪谱参数见表2。

沿船长方向取17个参考截面，采用JONSWAP谱做短期预报[9-10]。

重点考虑距船尾船首1/4L处剪力和船中位置弯矩，得到的RAO如图4～图6所示。重点位置短期统计极值见表3，运动加速度极值见表4。

表2 波浪谱参数

3.5 规范计算法与直接计算法比较

挪威船级社对于长度大于100 m的船舶提供了载荷的规范值[11]。

静水剪力为正时，

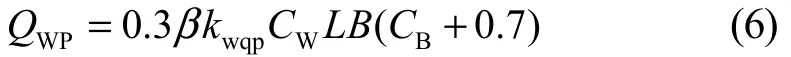
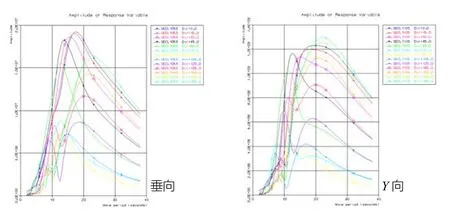
图4 典型垂向剪力和Y向弯矩RAO曲线

图5 压载工况下垂荡、纵摇、横摇RAO曲线

图6 满载工况下垂荡、纵摇、横摇RAO曲线

表3 重点位置短期统计极值

表4 运动加速度极值

静水剪力为负时，

将规范推荐值和直接计算得到的数值相比较，所得结果如图7所示。

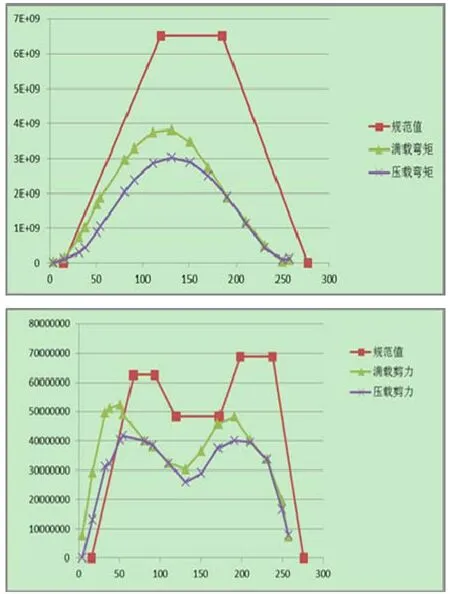
图7 2种装载下波浪载荷与规范值的比较

1）满载工况下的波浪载荷比压载工况下的大很多。这是因为满载时吃水增加会承受更大的波浪力，然而在压载工况下船体运动加速度相对更大。

2）满载工况下传递函数的峰值区要比压载工况下的尖锐，满载工况下传递函数的最大值对应的波浪周期在12 s～14 s之间，压载工况下传递函数最大值所对应的波浪周期为14 s～16 s。由于FPSO满载状态下的总惯性矩更大，导致满载状态的固有周期大于压载工况下的固有周期。

3）对比2种工况下FPSO的传递函数，可以发现较大的垂荡、横摇和纵摇运动幅值主要集中在12 s～16 s之间的波浪周期范围内，波长范围大约在176 m～235 m，而对于波浪载荷而言，主要幅值集中在17 s～22 s之间，波长范围为249 m～323 m。

4）从计算结果来看，大部分位置产生的弯矩和剪力均小于规范推荐值，说明对于水深吃水比在1.4左右的船舶而言，规范值还是相对保守的。但是在船体尾部剪力有一个突变，甚至大于规范推荐值，这是因为规范公式并未包含水深项，而FPSO的装载量要求及水平尺度都很大，这就导致其结构刚度相对剪切刚度降低，浅水效应放大了波浪载荷值，这在实际设计时应受到重视。

4 结论

1）前期的设计工况单一考虑满载或压载都是不合理的。对于对载荷敏感的船体结构而言，应选取满载工况为设计工况；对于对运动敏感的上部组块设计而言，压载工况应被选为设计工况。

2）当浅水大型 FPSO遭遇的波长与船长接近时，载荷幅值最大。

3）进行结构设计时，对于船体中部货油舱的舱段分析，可以以载荷规范值作为设计值；对于首尾部线型过渡明显的区域，则需根据载荷预报评估来确定设计载荷值。

4）渤海地区良好的海况使得载荷统计值远小于规范值。这说明对于主要承担总纵强度的货油舱区域而言，其结构选型可以适当趋于临界以保证其经济性。而浅水效应下尾部剪力加大的情况，可以通过适当增加船尾横舱壁数量的方法来解决。这在前期总体布置规划中可以给予适当考量。