三元概念的一种构造方法
2019-04-18李俊余吴伟志
王 霞 江 山 李俊余 吴伟志
1(浙江海洋大学数理与信息学院 浙江舟山 316022)2 (浙江省海洋大数据挖掘与应用重点实验室(浙江海洋大学) 浙江舟山 316022)
哲学上认为一个“概念”是一个思想单元,它由外延和内涵2部分构成.基于概念的哲学观点,1982年德国数学家Wille提出了形式概念分析[1-2],它是数据分析、知识发现和知识处理的一种有效的数学工具.形式概念分析有2个基本概念:由对象集、属性集和二元关系构成的形式背景(二元背景) 和由外延和内涵构成的形式概念(二元概念).基于皮尔斯范畴三分理论,1995年 Wille等人[3]提出了三元概念分析,它是一种数据分析和信息处理的新方法.三元概念分析的基本概念是三元背景和三元概念.三元背景由对象集、属性集、条件集和三元关系构成,它可以看作是在二元背景的基础上添加了条件集.因此,三元背景考虑的是在哪些条件下一个对象具有某个属性.而三元概念是由外延、内涵和方式3部分构成的一个三元组.
魏玲等人[4-5]介绍了2014年以前有关三元概念分析的基本理论、方法及应用,主要概括为:概念三元格的构造[3,6-8]、三元蕴含及关联规则挖掘[9-11]、三元模态算子[12]、三元概念聚类[13-15]、三元背景的因子分析[16-19]及模糊化[20-24]等.此外,文献[25]证明了一个三元幂形式背景族的所有三元概念图构成一个完备格.汤亚强等人[26]研究了三元形式概念分析下的认知系统模型.文献[27]提出了三元标记数据分类问题的几种算法.基于三元形式概念分析,文献[28]给出了一种有效K-团动态检测定理.文献[29]利用三元形式概念分析提出了一种基于角色的访问控制的模型.文献[30]将粗糙集上、下近似算子引入到三元概念分析中,提出了对象定向三元概念和属性定向三元概念,推广了三元概念分析.为了简化三元背景和概念三元格的表达方式,祁建军等人[31]提出了一种三元背景和概念三元格的信息简化方法.应用三元概念分析,李贞等人[32]提出了文本分类方法.
相较于形式概念分析来说,有关三元概念分析的理论研究和实际应用都比较少,主要原因是三元概念的构造更加繁琐.众所周知:在形式概念分析中,任意一个外延非空的二元概念均可以由某些对象二元概念生成,因此对象二元概念在概念格的构造以及知识发现等方面都具有重要的作用.受此启发,本文通过研究对象-条件三元概念(即由单个对象和单个条件生成的三元概念)的特性来寻找构造三元概念的简单方法.研究表明:任意一个外延和方式非空的三元概念均可以由某些对象-条件三元概念生成.因此,类似于对象二元概念,对象-条件三元概念在三元概念的构造以及知识发现等方面具有同样重要的作用.此外,本文的另一个工作是研究当一个三元概念的外延、内涵和方式中有空集时的判定方法.
1 相关工作
本节给出形式概念分析和三元概念分析的基本概念和结论.
1.1 形式概念分析相关知识
定义1[3]. 形式背景.称(G,M,I)为一个形式背景(二元背景),其中G是一个对象集,M是一个属性集,I是G和M之间的一个关系.分别称G和M的元素为对象和属性.
若对象g和属性m具有关系I,则记为gIm.
定义2[3]. 形式概念.设(G,M,I)为一个二元背景,X⊆G,B⊆M.若二元组(X,B)满足:X′=B,B′=X,则称(X,B)为形式概念(二元概念),其中:
X′={m∈M|∀g∈X,gIm},
B′={g∈G|∀m∈B,gIm}.
设T=(G,M,I)是二元背景,对任意的二元概念(X1,B1),(X2,B2)定义偏序关系为
(X1,B1)≤(X2,B2)⟺X1⊆X2(⟺B1⊇B2).
记L(G,M,I)或L(T)为二元背景T=(G,M,I)中所有二元概念构成的集合.容易证明L(T)是格,称其为二元背景T的概念格.在概念格L(T)上定 义上、下确界为
(X1,B1)∧(X2,B2)=(X1∩X2,(B1∪B2)″),
(1)
(X1,B1)∨(X2,B2)=((X1∪X2)″,B1∩B2),
(2)
则概念格L(T)是一个完备格.
∀g∈G,(g″,g′)∈L(T),称其为对象二元概念.
性质1[3]. 设T=(G,M,I)是一个二元背景,X,X1,X2为任意的对象子集,B,B1,B2为任意的属性子集,则有下列7条性质成立:


2)X⊆X″,B⊆B″.
3)X′=X‴,B′=B‴.
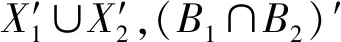

6) (X″,X′)∈L(T).
7)X⊆B′⟺B⊆X′.
1.2 三元概念分析相关知识
定义3[3]. 三元背景.称=(K1,K2,K3,Y)为三元背景,其中K1,K2,K3为非空集合,Y为K1,K2,K3之间的关系,即Y⊆K1×K2×K3.分别称K1,K2,K3为对象集、属性集和条件集.分别称K1,K2,K3的元素为对象、属性和条件.
若对象g、属性a和条件c具有关系Y,则记为(g,a,c)∈Y,表示对象g在条件c下具有属性a,通常在三维交叉表的相应位置用“×”标出.
X(i)={(aj,ak)∈Kj×Kk|∀ai∈Ki,
ai,aj,ak具有关系Y},
Z(i)={ai∈Ki|∀(aj,ak)∈Z,
ai,aj,ak具有关系Y}.
注:根据(i)-诱导算子的定义可知,(i)-诱导算子相当于二元背景(i)=(Ki,Kj×Kk,Y(i))上的′算子,其中∀ai∈Ki,∀aj∈Kj,∀ak∈Kk有aiY(i)(aj,ak)等价于ai,aj,ak具有关系Y.
另外,Xi⊆Ki,Xj⊆Kj,Ak⊆Kk定义(i,j,Ak)-诱导算子为


注:(i,j,Ak)-诱导算子相当于二元背景=(Ki,Kj,)上的′算子,其中∀ai∈Ki,∀aj∈Kj有(ai,aj)∈等价于∀ak∈Ak,ai,aj,ak具有关系Y.
定义4[3]. 三元概念.设=(K1,K2,K3,Y)是一个三元背景,称(A1,A2,A3)为三元背景的一个三元概念,如果对任意的{i,j,k}={1,2,3},j bik(Xi,Xk)(A1,A2,A3),i≠k, 其中,AjXi(i,j,Xk),AiAj(i,j,Xk),Ak(Ai×Aj)(k). 命题1[6]. 设=(K1,K2,K3,Y)是一个三元背景,Xi⊆Ki,Xk⊆Kk,{i,j,k}={1,2,3},则有bik(Xi,Xk)=(A1,A2,A3)∈J(). ∀(B1,B2,B3)∈J(),若Xi⊆Bi,Xk⊆Bk,则Bj⊆Aj,且当Bj=Aj时,Ai⊇Bi,Ak⊆Bk. 一般来说,bik(Xi,Xk)≠bki(Xk,Xi),i≠k. 特别地,若(A1,A2,A3)∈J(),则bik(Ai,Ak)=bki(Ak,Ai)=(A1,A2,A3). ∀C⊆Kk,由(i,j,C)-诱导算子和(i)-诱导算子的定义可知,∀A⊆Ki,∀C⊆Kk有(A×C)(j)=A(i,j,C).所以,为书写方便起见,将(i,j,C)-诱导算子和(i)-诱导算子统一定义为A(C)(A×C)(j)=A(i,j,C). 考虑到二元概念中有上述2类特殊的概念,本节研究三元概念中是否也存在类似的2类三元概念.对比外延为空集的二元概念,研究外延、内涵和方式中有空集的三元概念具有的性质及判定方法.对比对象二元概念,在三元概念中寻找有类似作用的三元概念,可以通过这类三元概念生成剩余的三元概念. 下面考虑三元概念的外延、内涵和方式中有空集时具有的性质. 引理1. 设=(K1,K2,K3,Y)是一个三元背景,有3条成立: 证明. 1)⟸若存在g∈K1使得∀(a,c)∈K2×K3有(g,a,c)∈Y,则根据定义4三元概念的定义可知,∀(A1,A2,A3)∈J()有g∈A1,即A1≠∅. ⟹(反证法) 若∀g∈K1,总存在(a,c)∈K2×K3使得(g,a,c)∉Y,则b23(K2,K3)=(∅,K2,K3),这与J()中所有三元概念的外延均不为∅矛盾. 类似地可以证明2)和3). 证毕. 引理1也可以理解为3条结论: 引理2给出了引理1的另一种等价的表达形式. 引理2. 设=(K1,K2,K3,Y)是一个三元背景,(A1,A2,A3)∈J(),则有3条成立: 1)A1=∅⟺A2=K2,A3=K3. 2)A2=∅⟺A1=K1,A3=K3. 3)A3=∅⟺A1=K1,A2=K2. 定义5. 对象-条件三元概念.设=(K1,K2,K3,Y)是一个三元背景.∀(gi,ck)∈K1×K3,记 (3) 并称b13(gi,ck)为由对象gi和条件ck确定的对象-条件三元概念. 所有的对象-条件三元概念构成的集合记为OC={b13(gi,ck)|∀(gi,ck)∈K1×K3}. 定理1. 设=(K1,K2,K3,Y)是一个三元背景,∀(A,C)⊆K1×K3,A≠∅,C≠∅,定义: ∨O C{b13(g,c)|(g,c)∈A×C}=(B1,B2,B3), (4) 其中: 则(B1,B2,B3)∈J(). 综上所述,(B1,B2,B3)∈J(). 证毕. 定理1说明:对象-条件三元概念通过∨O C-运算可以生成一个三元概念. 下面定理2说明任意一个三元概念若它的外延和方式均为非空集合,则它可以由某些对象-条件三元概念通过∨O C-运算生成. 定理2. 设=(K1,K2,K3,Y)是一个三元背景,(A1,A2,A3)∈J(),且A1,A3为非空集合.则有(A1,A2,A3)=∨O C{b13(g,c)|(g,c)∈A1×A3}. 证明. 由定理1知,∨O C{b13(g,c)|(g,c)∈A1×A3}∈J(),将其记为(B1,B2,B3).下面证明:(B1,B2,B3)=(A1,A2,A3). 首先证明A2=B2.因为(A1,A2,A3)∈J(),所以若a∈A2,则∀(g,c)∈(A1,A3)有(g,a,c)∈Y,即∀(g,c)∈(A1,A3)有a∈g(c).从而,A2⊆g(c).于是,A2⊆B2.另一方面,若a∈B2,则∀(g,c)∈(A1,A3)有a∈g(c).即∀(g,c)∈(A1,A3)有(g,a,c)∈Y,所以a∈A2.从而,B2⊆A2.再结合A2⊆B2可得,A2=B2. 再来证明A3=B3.因为(A1,A2,A3)∈J(),所以若c∈A3,则∀(g,a)∈(A1,A2)有(g,a,c)∈Y,即∀g∈A1有从而,A3⊆于是,A3⊆∀g∈A1}=∩{g(B2)|∀g∈A1}=B3. 证毕. 结合定理1和定理2可得推论1. 推论1. 设=(K1,K2,K3,Y)是一个三元背景, J(){(∅,K2,K3),(K1,K2,∅)}= 二元背景是由对象集和属性集构成的二维交叉表.三元背景可以看作是在二元背景的基础上添加了条件集后的三维交叉表.因此,一个三元背景可以根据它的每一个条件分解成一系列的二元背景.设=(K1,K2,K3,Y)是一个三元背景,其中K1={g1,g2,…,gr},K2={a1,a2,…,as},K3={c1,c2,…,ct},其中r,s,t均为正整数.按照条件集K3的t个元素将三元背景分解为t个二元背景,分别记为 2) ∀ck∈K3,若(A1,A2)∈L(则),即的任意一个二元概念都是三元背景的某个三元概念的外延和内涵. 下面给出构造三元概念的4个步骤. 步骤1. ∀ck∈K3,生成二元背景上所有的对象二元概念(,),∀gi∈K1. 步骤4. 根据引理1判断(∅,K2,K3),(K1,K2,∅)是否为三元概念. 如果概念格L(∀ck∈K3已知,则可将上述构造三元概念的步骤1~3进行简化,具体如下: 步骤2. 记: 本节利用文献[9]中的例子对第2节提出的三元概念的构造方法作详细说明,并以此例简要说明所得三元概念在知识发现中的作用. 例1. 设=(K1,K2,K3,Y)是一个三元背景,其中对象集K1由耶稣12使徒构成,即K1={Peter,Andrew,James,John,Philip,Thomas,Matthew,James A (James Alphaeus),Thadaeus,Simon,Judas}.属性集K2由福音的36节构成,即K2={1,2,…,36},具体含义如表1所示.条件集K3由《马太福音》(MT)、《马可福音》(MK) 和《路加福音》(LK)构成,即K3={MT,MK,LK}. Table 1 The Attribute Set K2表1 属性集K2 Continued (Table 1) 另外,若在某个条件c∈K3下,12个对象均不具有某个属性a∈K2,则称该属性a为二元背景的冗余属性.表2~4所示3个二元背景均去掉了冗余属性以节省空间.如表2缺少属性3,6,9,13,14,17~23,25,33~36,则表示在二元背景中,12个对象均不具有这些属性,也就是说在《马太福音》中第3,6,9,13,14,17~23,25,33~36节中均没有提到耶稣12使徒中的任何1人.图1~3分别给出了3个二元背景的概念格. Table 2 The Dyadic Context 表2 二元背景 Table 2 The Dyadic Context 表2 二元背景 K1K2 without Redundant Attributes12457810111215162426272829303132Peter×××××××××××××Andrew××××James××××××John×××××Philip×Bartholomew×Thomas×Matthew××James A×Thadaeus×Simon×Judas××××× Note: “×” mean the persons are mentioned in the corresponding passages of MT Gospel. Table 3 The Dyadic Context 表3 二元背景 Table 3 The Dyadic Context 表3 二元背景 K1K2 without Redundant Attributes1234567811121315161724272829303133Peter××××××××××××××××Andrew××××××James×××××××××John×××××××××Philip×Bartholomew×Thomas×Matthew××James A×Thadaeus×Simon×Judas××× Note: “×” mean the persons are mentioned in the corresponding passages of MK Gospel. Table 4 The Dyadic Context 表4 二元背景 Table 4 The Dyadic Context 表4 二元背景 K1K2 without Redundant Attributes124567111213141524252729303134Peter×××××××××××××Andrew×James××××××John××××××××Philip×Bartholomew×Thomas×Matthew××James A×Thadaeus×Simon×Judas××× Note: “×” mean the persons are mentioned in the corresponding passages of LK Gospel. 步骤1. 由图1~3所示的所有对象二元概念生成14个对象-条件三元概念,具体为 Fig. 1 The concept lattice L()图1 概念格L() Fig. 2 The concept lattice L()图2 概念格L() Fig. 3 The concept lattice L()图3 概念格L() 1)b13({Philip},{MT})=b13({Philip},{MK})=b13({Philip},{LK})=b13({Bartholomew},{MT})=b13({Bartholomew},{MK})=b13({Bartholomew},{LK})=b13({Thomas},{MT})=b13({Thomas},{MK})=b13({Thomas},{LK})=b13({James A},{MT})=b13({James A},{MK})=b13({James A},{LK})=b13({Thadaeus},{MT})=b13({Thadaeus},{MK})=b13({Thadaeus},{LK})=b13({Simon},{MT})=b13({Simon},{MK})=b13({Simon},{LK})=b13({Andrew},{LK})=(K1,{7},K3); 2)b13({Matthew},{MT})=b13({Matthew},{MK})=b13({Matthew},{LK})=({Matthew},{5,7},K3); 3)b13({Peter},{MT})=({Peter},{1,2,4,7,8,10,11,12,15,27,28,30,31},{MT}); 4)b13({Andrew},{MT})=({Peter,James,John,Andrew},{1,4,7},{MT,MK}); 5)b13({James} ,{MT})=b13({John},{MT})=({James,John},{1,4,7,12,16,28},{MT,MK}); 6)b13({Judas},{MT})=({Judas},{7,24,26,29,32},{MT}); 7)b13({Peter},{MK})=({Peter},{1,2,3,4,6,7,8,11,12,15,17,27,28,30,31,33},{MK}); 8)b13({Andrew},{MK})=({Peter,James,John,Andrew},{1,2,4,7,17},{MK}); 9)b13({James},{MK})=({James,John},{1,2,4,6,7,12,16,17,28},{MK}); 10)b13({John},{MK})=({John},{1,2,4,6,7,12,13,16,17,28},{MK}); 11)b13({Judas},{MK})=b13({Judas},{LK})=({Judas},{7,24,29},K3); 12)b13({Peter},{LK})=({Peter},{1,2,4,6,7,11,12,15,25,27,30,31,34},{LK}); 13)b13({James},{LK})=({James,John},{1,4,6,7,12,14},{LK}); 14)b13({John},{LK})=({John},{1,4,6,7,12,13,14},{LK}). 步骤2. 由图1~3中剩余二元概念可生成5个不同的三元概念: 15) ({Peter,James,John},{1,4,7,12,28})|→({Peter,James,John},{1,4,7,12,28},{MT,MK}); 16) (∅,K2)|→(∅,K2,K3); 17) ({Peter,James,John},{1,2,4,6,7,12,17,28})|→({Peter,James,John},{1,2,4,6,7,12,17,28},{MK}); 18) ({Peter,John},{1,4,6,7,12,25})|→({Peter,John},{1,4,6,7,12,25},{LK}); 19) ({Peter,James,John},{1,4,6,7,12})|→({Peter,James,John},{1,4,6,7,12},{MK,LK}). 20) ∨O C{b13(g,c)|g∈{Peter},c∈{MT,MK}}=({Peter},{1,2,4,7,8,11,12,15,27,28,30,31},{MT,MK}); 21) ∨O C{b13(g,c)|g∈{Peter},c∈K3}=({Peter},{1,2,4,7,11,12,15,27,30,31},K3); 22) ∨O C{b13(g,c)|g∈{Peter},c∈{MK,LK}}=({Peter},{1,2,4,6,7,11,12,15,27,30,31},{MK,LK}); 23) ∨O C{b13(g,c)|g∈{John},c∈{MK,LK}}=({John},{1,4,6,7,12,13},{MK,LK}); 24) ∨O C{b13(g,c)|g∈{Peter,John},c∈K3}=({Peter,James,John},{1,4,7,12},K3). 步骤4. 由引理1可知,(K1,K2,∅)是的第25个三元概念,(K1,∅,K3)不是的三元概念. Fig. 4 The triadic diagram of the triadic context 图4 三元背景上的三元图 为了更直观地描述三元概念,图4给出了例1中25个三元概念构成的三元图.图4正上方的线图中每一个圆圈表示1个三元概念的方式,它包含该圆圈处所示的条件及其右侧线段相连处圆圈所示的条件(注意箭头所示方向),因此称正上方的线图为方式图.左下方的线图中每一个圆圈表示1个三元概念的内涵,它包含该圆圈处所示的属性及其左上方线段相连处圆圈所示的属性,称左下方的线图为内涵图.类似地,右下方的线图中每一个圆圈表示1个三元概念的外延,它包含该圆圈处所示的对象及其左下方线段相连处圆圈所示的对象,称右下方的线图为外延图.三元图中间的倒三角区域中每个圆圈代表1个三元概念,它通过虚线分别与外延图、内涵图和方式图中的圆圈相连,分别表示该三元概念的外延、内涵和方式.例如三元图中间倒三角区域从上面数第1行左侧第1个圆圈表示第1个三元概念,从上面数第2行左侧第2个圆圈表示第4个三元概念. 根据例1生成的三元概念,可以回答3个方面问题: 1) 在《路加福音》(LK) 中使徒James出现在哪几节?在这几节中还同时提到了哪些使徒?他们是否还在其他福音的这几节中出现? 由第13个三元概念可知,James出现在《路加福音》(LK) 的第1,4,6,7,12,14节;在这几节中同时提到了John;James和John只在《路加福音》(LK) 的这几节中出现. 2) James和John还同时在哪些福音的哪几节中出现?在这些福音书的这几节中是否还同时提到了其他使徒? 这些问题可以由第4,5,8,9,13,15,17,19,24个三元概念给出答案. 3) 基于对象的三元蕴含问题. (M×{a}×C)⊆Y⟹(N×{a}×C)⊆Y, 则称在条件集C下三元对象蕴含(M→N)C在中成立.特别地,当C=K3时,三元对象蕴含(M→N)C简记为M→N. 三元对象蕴含(M→N)C相当于二元背景下M和N之间的对象蕴含.所以,三元对象蕴含(M→N)C在中成立当且仅当N⊆M(C)(C).M(C)(C)恰好是由对象子集M和条件子集C生成的三元概念的外延,可由定理1和定理2生成.譬如,根据例1中第24个三元概念的生成过程可知:{Peter,John}(K3)(K3)={Peter,James,John},所以{Peter,John}→{James}成立,即在上述3本福音中只要提到使徒Peter和John的章节一定提到了使徒James. 注:形式背景的属性蕴含相关问题详见文献[1-2,33],三元蕴含相关问题详见文献[9-10]. 三元概念中有2类特殊的概念:外延、内涵以及方式中有空集的三元概念(如果存在的话)和对象-条件三元概念,因为剩余的三元概念均可以由某些对象-条件概念生成.本文给出了外延、内涵和方式中有空集的三元概念的判定方法,并提出了一种基于对象-条件三元概念生成剩余的三元概念的方法.在本文的基础上可以进一步考虑三元背景简化及规则获取等相关问题.2 三元概念的一种构造方法

2.1 一类特殊三元概念的性质
2.2 三元概念的构造方法
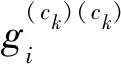



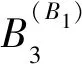


2.3 构造三元概念的步骤



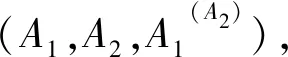


3 实 例










4 总 结
