划分序乘积空间：基于划分的粒计算模型

徐 怡 姚一豫

1(计算智能与信号处理教育部重点实验室(安徽大学) 合肥 230039)2(安徽大学计算机科学与技术学院 合肥 230601)3 (里贾纳大学计算机科学系 加拿大里贾纳 S4S0A2)

粒计算(granular computing)是用系统的、结构化的理解和方法来解决复杂问题的新理论、新技术和新方法[1-5]，被用于很多领域[6-10].粒计算的基本思想是在问题求解过程中通过构造信息粒，形成粒结构，基于粒结构从不同角度、不同层次上对现实问题进行描述、推理与求解[2,11-12].对复杂问题的全面理解通常是多视角的，从每一个视角着眼的理解又是多层次的，它的结果表现为一个多视角、多层次的粒结构.多层次强调对问题多个粒度层次的理解和描述.根据具体问题，不同的层次体现为不同的尺度、不同的复杂度、不同的抽象、不同的控制、不同的细节.多视角强调从多个不同的角度对问题进行描述和处理.从人类问题求解的角度看，对于同一个问题，不同的人会有不同的观点.人脑对于同一个问题有着不同的理解和处理方式.因此单视角对问题理解具有一定的局限性，需要多视角从全局的角度理解问题.多视角有2个优点：1)通过对问题的多样性描述，我们可以寻找解决问题的可能存在的最优化方法；2)多视角的组合可以给出任何一个单视角得不到的结果.粒计算的核心任务之一是通过信息粒化，构建多层次、多视角的粒结构[13].

粒、层和多层次是粒结构中的3个基本要素.粒是整体的一部分，可视为我们当前感兴趣的焦点，或者用于描述和表示的元素、概念、观念等，例如论域的子集、问题的子问题、系统的子系统等.一个层由一簇粒构成，层是粒化的结果.粒化是产生具有不同粒度层的过程，是建立粒结构的基础.粒化的程度通过粒度来刻画，表示层对问题观察或描述的抽象程度.多个层按照线性序关系组织起来构成了多层次.

对于不同的实际问题，信息粒化的方法多种多样.划分是一种常用的信息粒化方法.基于划分，姚一豫[13]提出了基于划分的粒计算模型.Pawlak[14]提出的粗糙集模型，张铃和张钹[15-16]提出的商空间模型都是基于划分的粒计算模型.但是现有对粒化方法的研究，主要是分别基于多层次的粒化方法和基于多视角的粒化方法，没有将多层次粒化方法和多视角粒化方法结合起来.基于多层次的粒化方法，粒化结果是一个多层次，多个层之间具有线性序关系.基于多视角的粒化方法，粒化结果是多个视角，但是每个视角仅有一个层.所以在本文中，为了更全面地理解和描述问题，从而可以更有效和合理地解决问题，给定一个论域，我们使用划分作为粒化方法，将多层次的粒化方法和多视角的粒化方法相结合，定义划分序乘积空间.首先，使用论域上的一个划分定义一个层.其次，使用一个嵌套的划分序定义一个多层次，表示为一个视角，层和层之间具有线性序关系.最后，给定多个视角，则定义了多个线性序关系，基于多个线性序关系的乘积，定义划分序乘积空间.划分序乘积空间给出了一种基于划分的粒计算模型.

在多层次粒化方法中，通常基于嵌套的属性序列或者嵌套的属性值序列来构建嵌套的划分序，即多层次.Marek和Rasiowa[17]基于递减的等价关系序列研究了集合的渐进近似.Pomykala[18]使用容差关系序列构建多层次.姚一豫[19]提出基于一个嵌套的等价关系序列诱导出多层次粒结构和层次粗糙集近似.粗糙集的属性约简，也是从一个嵌套的属性序列中找出一个最小的属性子集，使其分类能力和属性全集的分类能力相同，本质上也是一种多层次粒化方法[14,20].Hong等人[21]基于粗糙集，提出了从具有层次属性值的数据中学习多层次确定规则和可能规则的算法.Feng等人[22]研究了具有层次属性值的层次信息系统，提出了从不同的属性概念层自上而下的策略挖掘层次决策规则.Wu等人[23-24]从粒计算的角度研究了多尺度决策表，每个对象在每个属性下的属性值表示为具有不同粒度的多个尺度值.Ye等人[25]基于属性概念层次树，提出了多层次粗糙集模型.基于多层次粒结构，姚一豫[26]提出的序贯三支决策是一种有效且快速的决策策略.

基于多视角的粒化方法主要有以下研究工作.Qian等人[27-28]用一簇等价关系取代一个等价关系对论域进行分类和近似未知概念，提出了多粒度粗糙集模型.由于这一簇等价关系之间不存在线性序关系，所以这些等价关系不能构成多层次，因此多粒度粗糙集模型本质上是基于多视角的粒化方法，每个粒度对应一个视角.姚一豫等人[6]对已有的多粒度研究进行分类比较，提出了多粒度空间中粗糙集近似的统一框架，讨论了4种不同类型的粗糙集近似.Xu等人[29]基于支持特征函数和信息层，研究了广义多粒度粗糙集的上下近似集，给出了如何在广义多粒度粗糙集中选择最优粒度层的方法.利用多源近似空间表示多粒度空间，Khan和Banerjee[30]提出了强和弱上下近似集的概念.Sang等人[31]提出了基于多源决策系统的决策粗糙集模型，每个信息源对应问题的一个视角.Chen等人[32]基于多种形式的数据操作，提出了智能数据分析的多视角框架.

1 划分和划分序

划分是一种常用的信息粒化方法，划分通常可以由等价关系诱导得出.本节介绍和划分相关的基本概念[1-5].

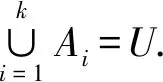
定义2. 细化.给定一个论域U，π1和π2是定义在U上的2个划分，π1={A1,A2,…,Ak}，π2={B1,B2,…,Bt},如果∀Bi∈π2,∃Aj∈π1,满足Bi⊆Aj，则称π2比π1细，或反之π1比π2粗，记为π2⪯π1.如果π2⪯π1并且π2≠π1,则称π2比π1真细，记为π2π1.

定义3. 划分序.给定一个论域U，P是定义在U上的一簇划分，P={π1,π2,…,πn}，如果其满足πn⪯πn-1⪯…⪯π1，则称P为一个嵌套的划分序.

划分可以由等价关系诱导得出.等价关系定义如下：

定义4. 等价关系.给定一个论域U，E⊆U×U是U上的一个等价关系，如果E是自反、对称且传递的.其中U×U表示U和U的笛卡儿积.[x]E={y∈U|(x,y)∈E}表示对象x∈U在等价关系E下的等价类，简记为[x].

定理1. 给定一个论域U，E是U上的一个等价关系，则E可以诱导出U上的一个划分π，记为π=UE={[x]E|x∈U}.

定理2. 给定一个论域U，E1和E2是定义在U上的2个等价关系，由E1和E2诱导出的2个划分记为π1和π2，其中，π1=UE1={[x]E1|x∈U}，π2=UE2={[x]E2|x∈U}.如果E2⊆E1，则π2⪯π1，且∀x∈U，[x]E2⊆[x]E1.

定理2说明等价关系之间的包含关系对应于划分之间的细化关系，基于一个细的等价关系产生的等价类比基于一个粗的等价关系产生的等价类小.

定义5. 等价关系序.给定一个论域U，R是定义在U上的一簇等价关系，R={E1,E2,…,En}，如果其满足En⊆En-1⊆…⊆E1，则称R为一个嵌套的等价关系序.

定理3. 给定一个论域U，R是定义在U上的一个嵌套的等价关系序，R={E1,E2,…,En}，满足En⊆En-1⊆…⊆E1，则由R可以诱导出U上的一个嵌套的划分序P={π1,π2,…,πn}，满足πn⪯πn-1⪯…⪯π1.

从定理3可以看出，一个嵌套的等价关系序可以诱导出一个嵌套的划分序.

注意：由于划分和等价关系是一一对应的，所以我们在本文中不加区分的使用这2个概念.

2 基于划分序乘积空间的粒计算模型

信息粒化是建立粒结构的基础.但是现有对粒化方法的研究，主要是分别基于多层次的粒化方法和基于多视角的粒化方法，没有将多层次粒化方法和多视角粒化方法结合起来.所以在本文中，为了更全面地理解和描述问题，从而可以更有效和合理地解决问题，给定一个论域，我们使用划分作为粒化方法，将多层次的粒化方法和多视角的粒化方法相结合，定义划分序乘积空间.划分序乘积空间给出一种基于划分的粒计算模型.

2.1 粒结构的3要素

粒、层和多层次是粒结构的3个基本要素.粒是整体的一部分，可视为我们当前感兴趣的焦点，或者用于描述和表示的元素、概念、观念等.一个层由一簇粒构成，每个层通过具有相似粒度的一簇粒对问题进行理解和表示.多个层按照线性序关系组织起来构成了多层次，即视角.在较粗的粒度层，我们通过忽略一些细节，对问题的表示较抽象和简洁，因此对问题的求解速度较快，但是精度较低.在较细的粒度层，我们对问题的表示较具体和详细，因此对问题的求解速度较慢，但是精度较高.

在粒结构的3要素中，层起到承上启下的作用.层是粒化的结果.对于不同的实际问题，粒化的方法多种多样.常用的粒化方法有基于划分或等价关系的粒化方法、基于覆盖的粒化方法、基于二元关系的粒化方法、基于模糊划分的粒化方法等.

但是现有的这些粒化方法，都是从多层次的角度和多视角的角度分别进行粒化，即对多层次的粒化方法和多视角的粒化方法分别进行研究，没有将二者结合起来.基于多层次的粒化方法，通常使用一个多层次来描述和解决问题，每个层对应论域的一个粒化结果，多个层之间具有线性序关系.基于多视角的粒化方法，通常使用多个视角来描述和解决问题，但是每个视角仅有一个层.因此导致现有的粒结构不能从多层次和多角度2个方面更全面系统地理解和描述问题，从而不能有效合理地解决问题.

2.2 基于划分的粒结构

在2.1节中我们给出了粒结构的一般描述，指出粒、层和多层次是粒结构的3个基本要素，粒化是建立粒结构的基础.但是没有考虑粒化的具体实现方法，因此粒、层和多层次缺乏具体的意义和解释.

如第1节所述，给定一个论域，划分和等价关系可以作为粒化方法对论域进行粒化.一个对论域的划分对应一个层，一个嵌套的划分序对应一个多层次，层和层之间的线性序关系可以解释为嵌套的划分序之间的细化关系.

因此，本节采用划分作为粒化方法，定义基于划分的粒结构.给出粒结构中构造粒、层和多层次的具体实现方法，从而赋予粒、层和多层次具体的意义和解释.

在基于划分的粒结构中，其3个要素具体描述为：

1) 粒.一个划分块(等价类)表示一个粒，记为[x]，x∈U.

2) 层.一个对论域的划分对应一个层，记为π={[x]|x∈U}.

3) 多层次.一个嵌套的划分序(一个嵌套的等价关系序),对应一个多层次，表示一个视角，记为P={π1,π2,…,πn}.

一般粒结构中的3要素和基于划分的粒结构中的3要素之间的对应关系如图1所示：

在基于划分的粒结构中，多层次对应的线性序关系是基于划分定义的细化关系，或者是基于等价关系定义的集合包含关系.

2.3 划分序乘积空间

为了更全面地理解和描述问题，从而可以更有效和合理地解决问题，给定一个论域，我们使用划分作为粒化方法，将多层次的粒化方法和多视角的粒化方法相结合，定义划分序乘积空间.

首先，使用论域上的一个划分定义一个层.其次，使用一个嵌套的划分序定义一个多层次，表示为一个视角，层和层之间具有线性序关系.最后，给定多个视角，则定义了多个线性序关系，基于多个线性序关系的乘积，定义划分序乘积空间.划分序乘积空间给出了一种基于划分的粒计算模型.

为了简单起见，我们首先定义包含2个视角的划分序乘积空间，然后再定义包含多个视角的划分序乘积空间.

在定义6中，2个嵌套的划分序P1和P2，定义了2个视角V1与V2，我们将其表示为2个全序集，全序集中的元素是层，全序关系是层和层之间的粗化细化关系.2个视角的划分序乘积，定义了包含2个视角的划分序乘积空间.

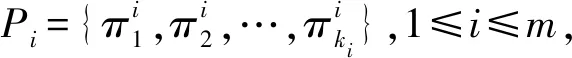
POPSm由m个视角的乘积构成，不同视角提供了对问题不同角度的理解和描述.每个视角又可以从多个粒度层次上对问题进行理解和描述.因此划分序乘积空间提供了对问题多层次多视角的理解和描述.

定理4. 划分序乘积空间POPSm=(×Pi,⪯P)是一个格结构.

证明. 基于定义7，⪯P是一个偏序关系，其满足自反性、反对称性和传递性.因此，POPSm是一个偏序集.为了进一步证明POPSm是一个格结构，我们只需要证明对于POPSm中任意2个元素，它们有上确界和下确界.

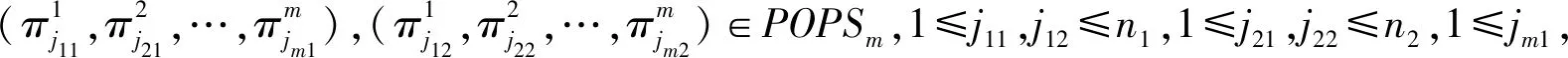
证毕.

在划分序乘积空间中，其问题求解空间为一个格结构，格中的每一个节点对应一个问题求解层，定义如下:

每个问题求解层，一方面通过多视角给出了对问题的多样性描述，另一方面基于每个视角，我们可以得到一个问题求解结果.因此，基于每个问题求解层，在实际求解问题时有3种处理策略：

1) 首先融合多个视角对问题的描述，然后基于融合后的描述结果进行最终的问题求解，我们称之为多视角问题描述的融合.

2) 首先分别基于单个视角对问题进行求解，然后融合多个视角对问题求解的结果进行最终的问题求解，我们称之为多视角问题求解结果的融合.

3) 在多视角问题求解过程中，同时对问题描述和求解结果进行融合，我们称之为多视角问题求解过程的融合.

例如在划分序乘积空间中，我们可以对每一个视角从顶层到底层按照粒度递减的顺序来寻找一个合适的层进行问题求解，然后融合多个视角下各个层的求解结果进行最终的问题求解，即为多视角问题求解结果的融合.在多粒度粗糙集模型中，Qian等人[27-28]提出了基于求同存异的乐观融合策略和求同排异的悲观融合策略，张明等人[33-34]提出了基于可变多粒度的融合策略，都属于多视角问题求解结果的融合.

注意：当划分序乘积空间中视角的个数为1时，划分序乘积空间退化为现有的多层次的粒结构.当划分序乘积空间中每个视角的层数为1时，划分序乘积空间退化为现有的多视角的粒结构.

划分序乘积空间采用划分作为粒化方法.当我们采用其他粒化方法时，可以得到各种类型的序乘积空间，如覆盖序乘积空间、邻域序乘积空间、模糊序乘积空间等.

2.4 实 例

本节中我们通过一个例子来说明划分序乘积空间在实际应用中的优越性.

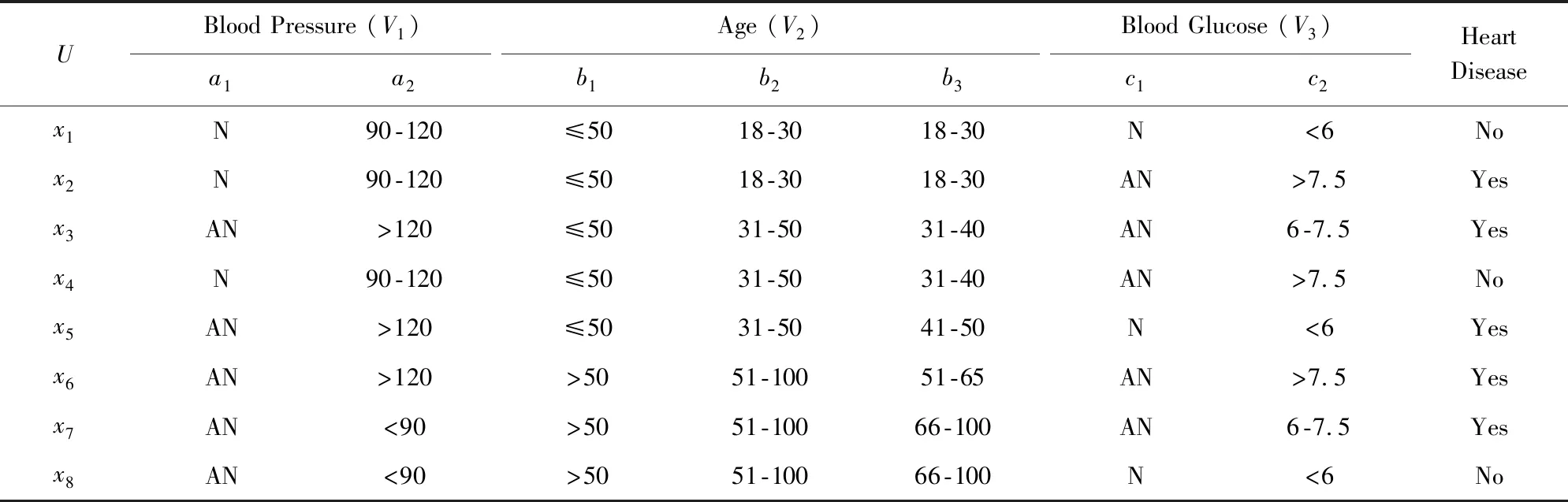
Table 1 Information of Patients表1 病人信息表

Note: N means normal; AN means abnormal.

对于V1，其2个层描述为

对于V2，其3个层描述为

对于V3，其2个层描述为

由3个视角构成的划分序乘积空间POPSm=(×Pi,⪯P)构成的格结构如图2所示：

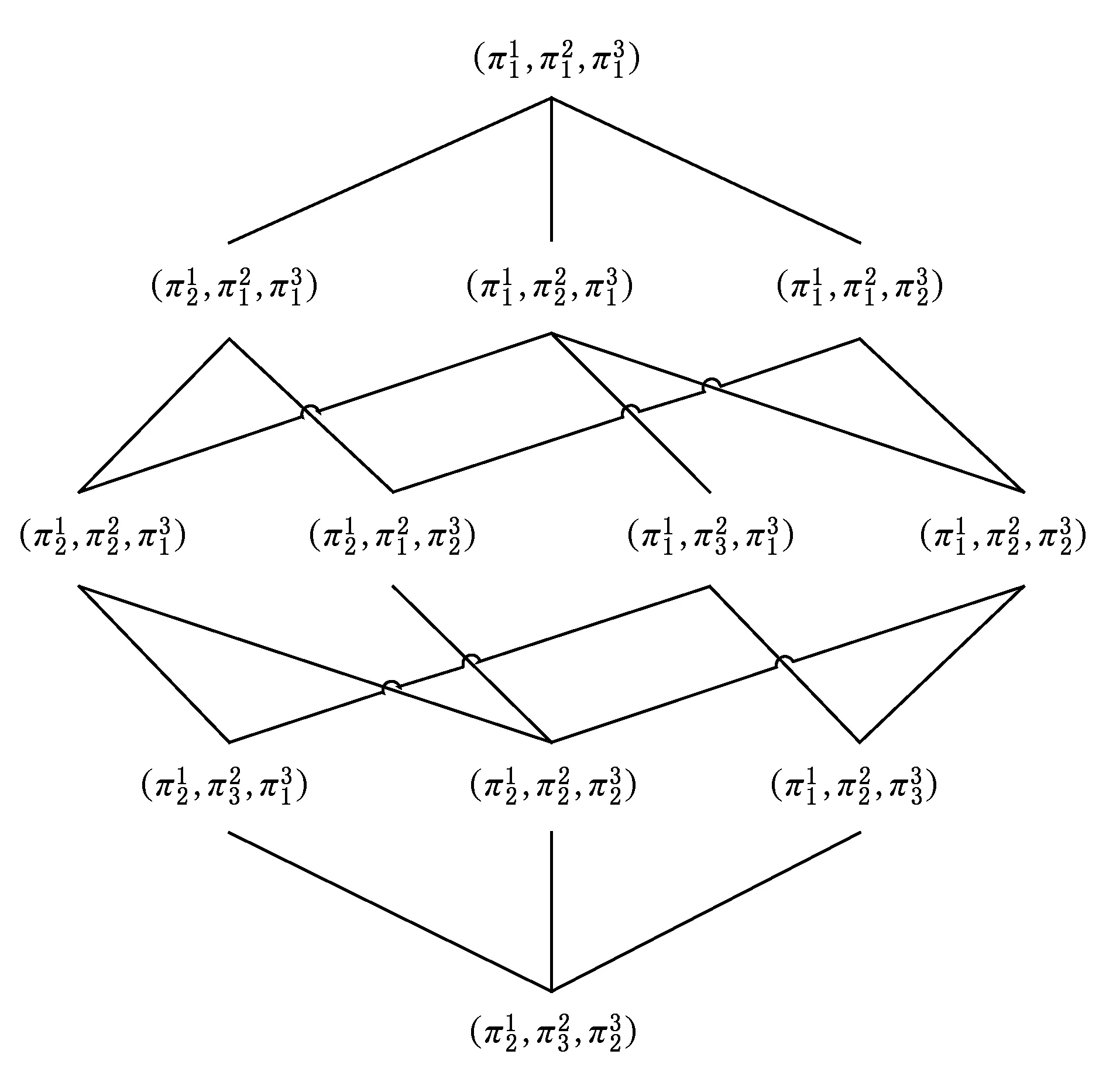
Fig. 2 Partition order product space with three views图2 由3个视角构成的划分序乘积空间

通过图2可以看出，划分序乘积空间同时考虑了多层次的粒化方法和多视角的粒化方法，共有12个问题求解层.因此，医生在实际诊断病人时，不仅可以从多个层次上处理问题，还可以从多个角度处理问题，根据实际问题求解的需要，可以在不同视角和同一视角的不同层次之间灵活选择和变换，从而使得对疾病的诊断更加有效和合理.在实际问题求解中，如何在划分序乘积空间中找到合适的问题求解层，将是一个值得研究的方向.

3 结 论

粒计算研究有效的粒结构用于问题求解和信息处理，多层次和多视角是其2个重要的粒化原则.但是现有对粒结构中粒化方法的研究，主要是分别基于多层次的粒化方法和基于多视角的粒化方法，没有将两者结合起来.所以在本文中，为了更全面地理解和描述问题，从而可以更有效和合理地解决问题，给定一个论域，我们使用划分作为粒化方法，将多层次的粒化方法和多视角的粒化方法相结合，定义划分序乘积空间.首先，使用论域上的一个划分定义一个层.其次，使用一个嵌套的划分序定义一个多层次，表示为一个视角，层和层之间具有线性序关系.最后，给定多个视角，则定义了多个线性序关系，基于多个线性序关系的乘积，定义划分序乘积空间.证明了划分序乘积空间是一个格结构.已有的基于多层次的粒化方法得到的粒结构和基于多视角的粒化方法得到的粒结构是划分序乘积空间的特殊情况.

划分序乘积空间给出了一种新的粒计算模型，在此基础上，我们可以研究基于划分序乘积空间的三支决策模型、基于划分序乘积空间的粗糙集模型、基于划分序乘积空间的概念格模型等，从而给出各种多层次多视角的问题求解策略和方法.在以后的工作中，我们将进一步研究划分序乘积空间的拓扑结构和相关性质.