基于引导信号修正的时域干扰阻塞方法

郑恩明， 陈新华， 李嶷

(中国科学院声学研究所, 北京 100190)

0 引言

在线列阵接收数据中，真实目标信号往往会被强干扰所掩盖，使得目标探测与跟踪非常困难。研究如何阻塞强干扰，提高对弱目标的探测能力显得尤为重要，尤其是当存在宽带干扰时[1-9]。

阻塞矩阵方法因运算量小，常被工程应用[7-9]，该方法最早被用于解决波束形成中协方差矩阵估计时的信号混入问题，然后被用于干扰阻塞方面研究[10-13]，被称为干扰阻塞方法(本文在时域上对干扰进行处理，称其为“时域干扰阻塞方法”)。干扰阻塞方法是通过阻塞矩阵实现对预知方位的干扰抑制，会对线列阵接收数据造成一定自由度损失，改变了线列阵接收信号原始形态，在部分区间降低了对目标的探测性能[14]。为了进一步阐述干扰阻塞方法对目标信号探测性能的影响，许稼等[15]和高阳等[16-17]利用输出信干噪比增益、波束图对该方法抗干扰性能进行衡量，分析了干扰阻塞方法存在的问题及适用性，但并未给出改善方法。为了改善干扰阻塞方法对干扰邻近弱目标的探测性能，葛士斌等[18-19]从协方差矩阵上进行分析论证，通过加大干扰阻塞所用阵元间距，减小了干扰附近的衰减区间，提高了对干扰邻近弱目标的探测性能。但是该方法并未解决干扰阻塞方法形成的“宽凹”或“凸”字型波束对目标探测结果的影响，且通过加大干扰阻塞所用阵元间距也会造成类似栅瓣现象的存在，影响对弱真目标的探测。

针对时域干扰阻塞方法导致的波束畸变和探测盲区问题，本文依据干扰阻塞方法形成的“宽凹”或“凸”字型波束与干扰形式无关，只与处理数据频带、干扰角度有关(在线列阵确知情况下)[20]，提出一种基于引导信号修正的时域干扰阻塞方法。该方法采用由引导信号形成的衰减曲线对时域干扰阻塞方法进行非线性化处理，降低了时域干扰阻塞方法对线列阵波束形成输出信号能量造成的影响，在时域上对干扰阻塞方法输出波束实现了校正，降低了“宽凹”或“凸”字型波束对目标探测结果的影响。通过数值仿真和海试数据处理进行进一步验证，本文方法通过引导信号有效地减小了时域干扰阻塞方法对波束形成输出信号能量造成的衰减区间，对原衰减区间内的弱目标实现了有效探测。

1 时域干扰阻塞方法

以一个干扰和一个目标情况为例，对其进行分析论述，其他情况可由该情况进行遍历。在t时刻，相对等间距线列阵(接收阵)首端方向，有弱目标s(t)从方位角θ1入射，干扰角i(t)从方位角θ0入射，则线列阵第k个阵元拾取的数据xk(t)可表示为

(1)

式中：1≤k≤K为线列阵阵元数；d为阵元间距；c为声速；nk(t)为第k个阵元拾取的加性高斯白噪声。

第k+1个阵元在t时刻拾取的数据xk+1(t)为

(2)

将第k+1个阵元拾取数据相对第k个阵元拾取数据延迟时间τk+1,k与第k个阵元拾取数据相减可得新数据yk(t)为

(3)

当τk+1,k=dcosθ0/c时，由(3)式得到的新数据可表示为

(4)

将yk(t)按频域形式可表示为

(5)

式中：ω=2πf为数据角频率，f为频率；Nk(ω)为第k个阵元拾取的背景噪声功率谱。

由(5)式可知，yk(t)中的目标信号相对于真实目标信号s(t)也发生了失真。下面将进一步讨论s(t)中目标信号的变化情况。

2 目标信号能量变化分析

2.1 理论分析

由理论分析可知，干扰阻塞后，目标信号相对于真实目标信号s(ω)发生了(1-ejωd(cos θ1-cos θ0)/c)的变化。为了更直观地分析时域干扰阻塞方法对波束形成输出造成的影响，接下来从线列阵波束形成输出信号和噪声变化上进行分析论述，以便得到改善时域干扰阻塞方法。

令线列阵各阵元拾取干扰、信号和背景噪声，背景噪声和背景噪声之间相关性为0，干扰阻塞前，波束形成在扫描角度为θ，θ∈[0°,180°]上输出信号、噪声能量分别为

(6)

式中：τk=(k-1)dcosθ/c为波束形成第k个阵元相对参考阵元(本文选第1个阵元为参考阵元)进行的延时，T为一次处理数据采样长度。

为了更好说明，将(6)式按频域形式表示为

(7)

式中：ωl为数据处理所用滤波器下限；ωh为数据处理所用滤波器上限；(·)*为共轭函数；M为快速傅里叶变换长度；同一背景下，可令N(ω)=Nk(ω)为各阵元拾取的背景噪声功率谱。

同理，干扰阻塞后，波束形成在扫描角度θ上输出信号、噪声能量分别为

(8)

同样，将(8)式按频域形式表示为

(9)

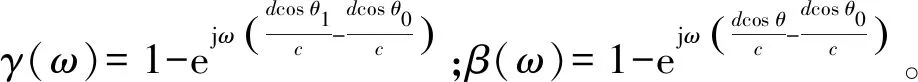
对比(7)式和(9)式可知，干扰阻塞前后，波束形成输出信号能量变化与γ2(ω)有关，噪声能量变化与β2(ω)有关。

当扫描角度θ=θ1时，(7)式和(9)式可进一步表示为

(10)

(11)

对比(10)式和(11)式可知，干扰阻塞前后，波束形成在目标方向θ1上输出信号、噪声能量变化可表示为

(12)

由(12)式所示函数可知，时域干扰阻塞方法对波束形成输出信号能量、噪声能量造成的变化主要与γ2(ω)有关，其变化趋势一致。对于确知线列阵，γ2(ω)主要与数据处理频带[ωl,ωh]、目标方位角θ1和干扰方位角θ0有关。

2.2 数值仿真分析

为了进一步验证时域干扰阻塞方法对波束形成输出信号能量、噪声能量造成的变化主要与γ2(ω)有关，且其变化趋势一致，进行如下仿真分析。仿真分析中阵元数K=64，阵元间距d=4 m，声速c=1 500 m/s，目标信号为宽带线性调频信号，背景噪声为高斯白噪声。接下来分析处理数据频带[ωl,ωh]、目标方位角θ1和干扰方位角θ0对波束形成输出信号能量、噪声能量造成的影响及其变化趋势。

1)数据处理频带为[100 Hz,200 Hz]。不同干扰方位角θ0情况下，波束形成输出信号能量、噪声能量在不同方位角θ1上的仿真结果如图1所示。

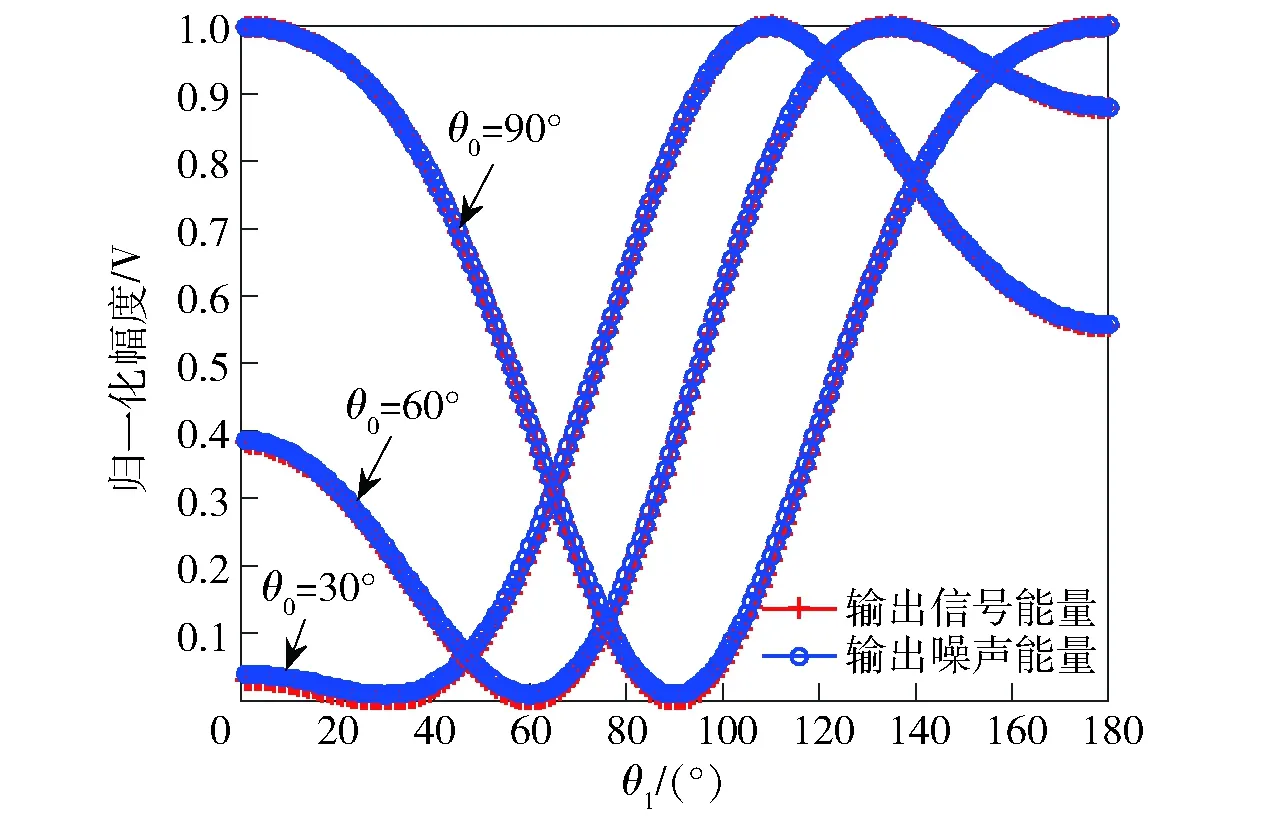
图1 输出信号和噪声量衰减区间(干扰方位变化)Fig.1 Attenuation intervals of output signal and noise energy (interference bearing change)

2)干扰方位角θ0=30°. 不同处理频带情况下，波束形成输出信号能量、噪声能量在不同方位角θ1上的仿真结果如图2所示。

图2 输出信号和噪声能量衰减区间(处理频带变化)Fig.2 Attenuation intervals of output signal and noise energy (processing frequency band change)

由图1和图2可知，时域干扰阻塞方法会对波束形成输出信号能量和噪声能量造成不同程度的衰减，输出信号能量和噪声能量在一部分方位区间被增强，而在另一部分方位区间被降低。由于输出信号能量的较大差异，将影响衰减区间对弱目标的探测，降低了弱目标探测性能。

3 基于引导信号修正的时域干扰阻塞方法

3.1 理论分析

由于实际数据处理中目标信号形式和方位角θ1未知，无法通过模拟处理频带目标信号作为引导信号修正干扰阻塞对波束形成输出信号能量的影响。但是由第2节理论分析和数值仿真结果可知，干扰阻塞前后线列阵波束形成输出信号能量、噪声能量变化趋势一致。对此，可通过模拟处理频带背景噪声作为引导信号修正干扰阻塞对波束形成输出信号能量的影响，在干扰角度处，通过干扰阻塞方法对噪声引导信号进行处理，得到干扰阻塞后输出能量变化趋势，然后依据输出能量变化趋势修正干扰阻塞对实际数据处理的影响。

为了能够真实模拟干扰阻塞对线列阵波束形成输出噪声能量的影响规律，本文采用事先录取的海洋背景噪声作为引导信号(也可通过模拟高斯白噪声作为引导信号)。按照第2节所示干扰阻塞方法，可得到阻塞θ0方位数据后的新数据为

(13)

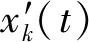
干扰阻塞后，波束形成在扫描角度θ上输出波束为

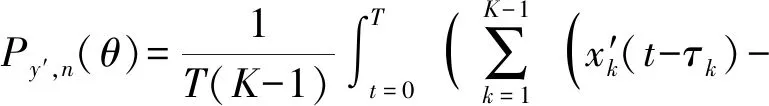
(14)

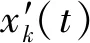
Kalman滤波是一组以递推关系给出随机系统状态的最优线性滤波算法，根据观测数据自动改变系数并保证下一时刻真实值均方误差最小[21]，本文接下来采用Kalman滤波对Py′,n(θ)进行光滑处理。

由于本文中所需滤波数据为一维非相关数据，其状态转移和观测方程模型可表示为

(15)

式中：S(θ)=Py′,n(θ)；v(θ)和w(θ)分别为状态噪声和观测噪声，其方差分别为Q和R.

Kalman滤波方程可表示为

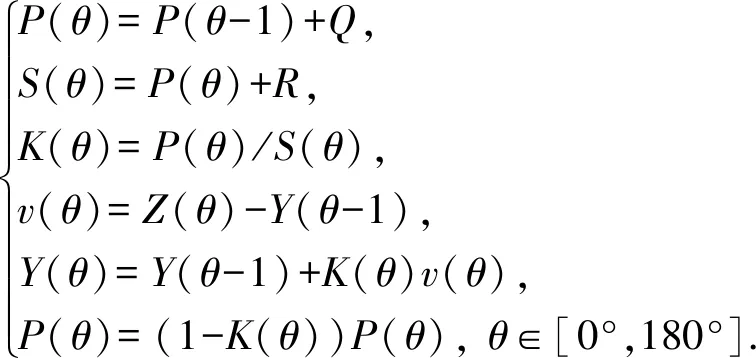
(16)

在(16)式Kalman滤波方程中，由于干扰阻塞引导信号后输出波束Py′,n(θ)存在一定波动，且波动带宽较宽，求取观测噪声方差R时，所用数据为[0°,180°]内所有数据；在求取状态噪声方差Q时，所用数据为该滤波点前后L个点数据(L根据实际干扰阻塞后波束“宽凹”或“凸”变化程度设置)；预测方差P(θ)初始值所用数据为干扰阻塞引导信号后输出波束Py′,n(θ)前L个点数据；状态初始更新值Y(θ)为干扰阻塞引导信号后输出波束Py′,n(θ)第1个点值。

利用Y(θ)作为衰减曲线，按(17)式对(8)式输出能量进行非线性化处理，可使干扰阻塞前后，线列阵波束形成输出信号能量比值近似为1，即经非线性化处理可有效降低时域干扰阻塞方法对线列阵输出信号能量造成的影响。

(17)

3.2 实现流程及运算量分析

由第3.1节理论分析可知，基于引导信号修正的时域干扰阻塞方法可分为如下步骤实现：

步骤2根据预设干扰阻塞角度θ0，按(14)式得到引导信号时域干扰阻塞后波束形成在扫描角度θ∈[0°,180°]上输出波束Py′,n(θ)；

步骤3利用第3.1节所述Kalman滤波方程和参数设置方法，对步骤2输出波束进行光滑处理，得到波束衰减曲线Y(θ)；

步骤4根据处理频带[ωl,ωh]对线列阵采集数据进行滤波处理，得到处理频带内数据xk(t)；

步骤5根据预设干扰阻塞角度θ0，按(8)式得到线列阵时域干扰阻塞后波束形成在扫描角度θ∈[0°,180°]上输出波束Py(θ)=Py,s(θ)+Py,n(θ)；

步骤7在处理频带[ωl,ωh]和干扰阻塞角度θ0未发生变化情况下，更新线列阵采集数据，重复步骤4～步骤6得到最新数据经干扰阻塞后波束形成输出结果；在处理频带[ωl,ωh]发生变化情况下，更新线列阵采集数据，重复步骤1～步骤6得到最新数据经干扰阻塞后波束形成输出结果；在处理频带[ωl,ωh]未发生变化，干扰角度θ0发生变化情况下，更新线列阵采集数据，重复步骤2～步骤6得到最新数据经干扰阻塞后波束形成输出结果。

由以上实现过程可知，在处理频带[ωl,ωh]和干扰阻塞角度θ0未发生变化情况下，本文方法相比时域干扰阻塞方法，只需在统计时间内对引导信号进行一次时域滤波、波束形成和Kalman滤波就行，在统计时间内增加运算量有限，可忽略不记；在处理频带[ωl,ωh]发生变化情况下，本文方法相比时域干扰阻塞方法，在统计时间内每次更新数据需要对引导信号进行一次时域滤波、波束形成和Kalman滤波，在统计时间内增加近1倍运算量；在处理频带[ωl,ωh]未发生变化，干扰角度θ0发生变化情况下，本文方法相比时域干扰阻塞方法，在统计时间内只需对引导信号进行一次时域滤波，每次更新干扰阻塞角度时，需要对滤波后引导信号进行波束形成和Kalman滤波，在统计时间内增加运算量1倍波束形成运算量和181个数据的Kalman滤波。

3.3 数值仿真分析

为了进一步验证本文方法可以有效地降低时域干扰阻塞方法对线列阵波束形成输出信号造成的影响，进行如下数值仿真分析。

令干扰信号频带、目标信号频带均为[100 Hz,200 Hz]，干扰与目标方位角分别为θ0=60°和θ1=63°，背景噪声为带宽[100 Hz,200 Hz]的高斯白噪声，声速c=1 500 m/s，阵元间距d=4 m，阵元数K=64. 目标与干扰谱级比为-20 dB，目标与背景噪声谱级比为-15 dB. 图3～图6为不同方法在处理频带[100 Hz,200 Hz]内对θ0=60°干扰阻塞前后所得结果，在时域滤波处理中滤波器阶数为256，Kalman滤波方程中L=10，其他相关参数根据(16)式描述所得。

图3 方位历程图(干扰阻塞前)Fig.3 Bearing-time history (before interference blocking)

图4 方位历程图(时域干扰阻塞方法)Fig.4 Bearing-time history (interference blocking in time domain)

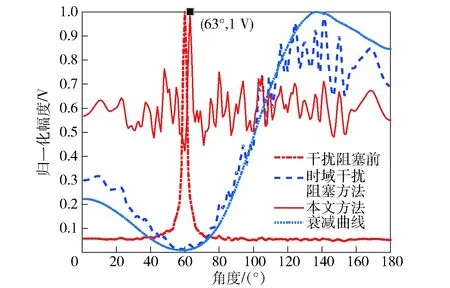
图6 波束图(t=1 s)Fig.6 Beam pattern (t=1 s)

由图3～图6可知：在阻塞干扰时，由于时域干扰阻塞方法会对线列阵波束形成输出信号能量造成不同程度的衰减，干扰阻塞后弱目标不能被有效探测；而本文方法采用了由引导信号形成的衰减曲线对时域干扰阻塞方法进行了非线性化处理，降低了时域干扰阻塞方法对线列阵波束形成输出信号能量造成的影响，在阻塞干扰时，原衰减区间内的弱目标可被有效探测。数值仿真结果验证了本文方法通过引导信号可有效地减小干扰阻塞衰减区间，实现波束校正，对原衰减区间内弱目标实现有效探测。

为了进一步验证2种方法检测不同位置处弱目标情况，进行如下数值仿真。仿真中令干扰、目标信号频带均为[100 Hz,200 Hz]，干扰方位角θ0=60°，目标方位角θ1为0°～180°，声速c=1 500 m/s，阵元间距d=4 m，阵元数K=64. 目标与干扰谱级比为-20 dB，目标与背景噪声谱级比为-15 dB，在时域滤波处理中滤波器阶数为256，Kalman滤波方程中L=10，其他相关参数根据(16)式描述所得。图7为θ1∈[1°,180°]时，2种方法进行200次独立统计所得检测弱目标成功概率。

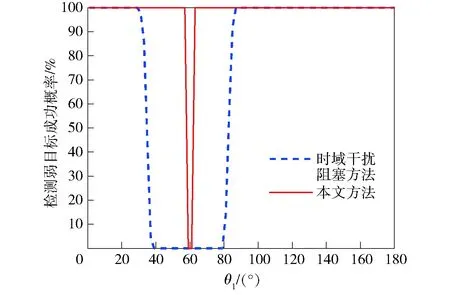
图7 检测弱目标成功概率Fig.7 Success probability of weak target detection

由图7可知，在本文仿真条件下，相比时域干扰阻塞方法，本文方法未成功检测目标(成功概率小于50%)对应方位区间宽度由40°缩小到5°.

3.4 海试数据处理

试验数据为2016年在南海进行目标探测试验所得。试验采用64元水平线阵接收信号，阵元间隔为4 m，水平线阵尾端方向设为180°.

数据处理实例1：处理频带为[40 Hz,50 Hz]，在时域滤波处理中滤波器阶数为256，Kalman滤波方程中L=10，其他相关参数根据(16)式描述所得。图8～图10分别为3种方法所得方位历程图，干扰阻塞角度有2个，分别为图8中20°～40°能量最大值对应角度θ0和θ0=160°.

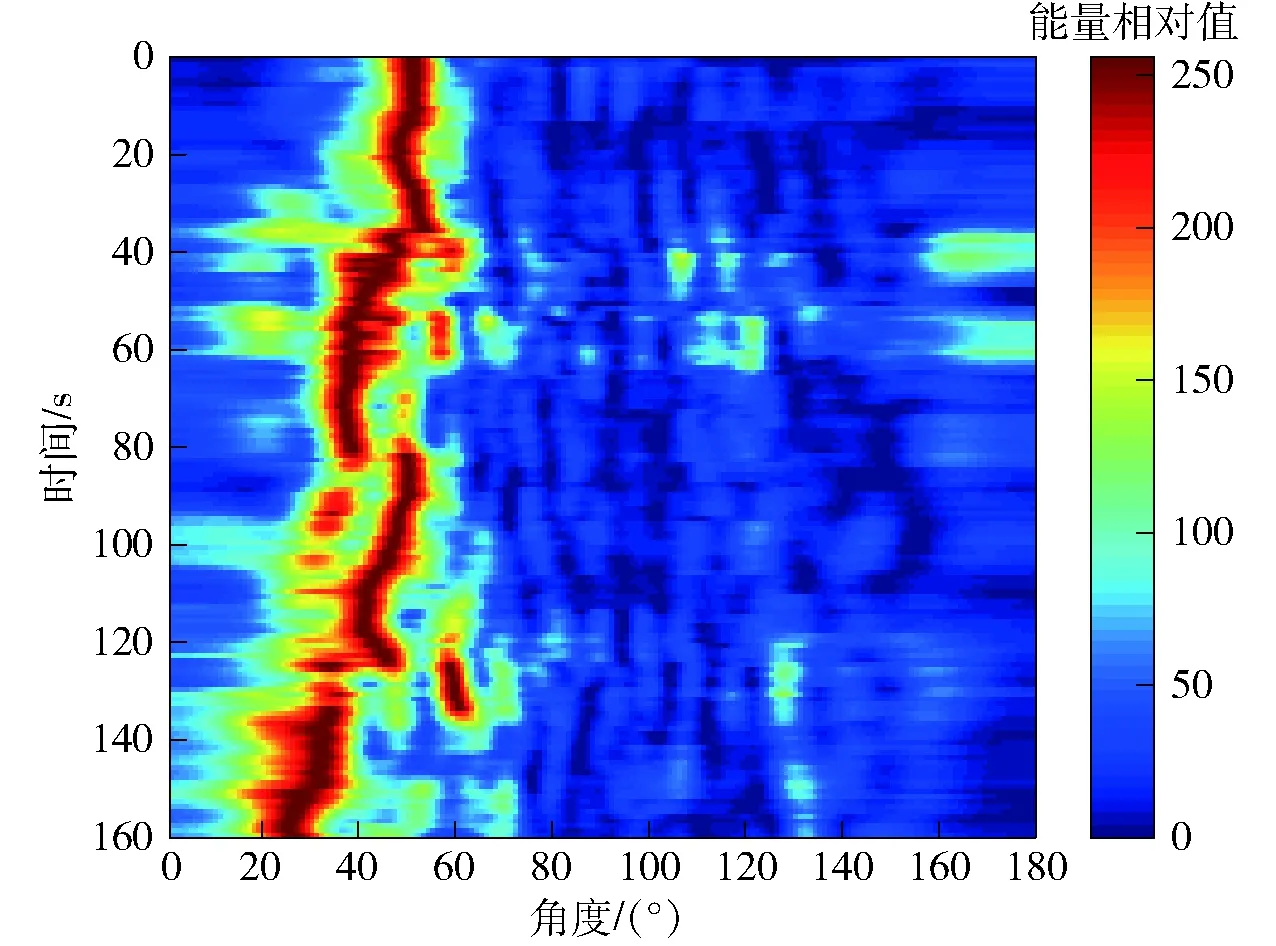
图8 方位历程图(干扰阻塞前)Fig.8 Bearing-time history (before interference blocking)

图9 方位历程图(时域干扰阻塞方法)Fig.9 Bearing-time history (interference blocking in time domain)

图10 方位历程图(本文方法)Fig.10 Bearing-time history (the proposed method)

由图8～图10可知：在阻塞θ0为20°～40°和θ0=160°干扰时，位于衰减区域内的θ1为100°～140°处目标不能被时域干扰阻塞方法实现有效探测；而本文方法利用了由引导信号形成的衰减曲线对时域干扰阻塞方法进行了非线性化处理，降低了时域干扰阻塞方法对线列阵波束形成输出信号能量造成的影响，位于原衰减区域内的θ1为100°～140°处目标被有效探测。试验数据1处理结果验证了本文方法通过引导信号减小了时域干扰阻塞衰减区间，实现了波束校正，对原衰减区域内的弱目标实现有效探测。

数据处理实例2：处理频带为[80 Hz,250 Hz]，在时域滤波处理中滤波器阶数为256，Kalman滤波方程中L=10，其他相关参数根据(16)式描述所得。图11～图13分别为3种方法所得方位历程图，干扰阻塞角度同样有2个，分别为图11中20°～40°能量最大值对应角度θ0和θ0=160°.

图11 方位历程图(干扰阻塞前)Fig.11 Bearing-time history (before interference block)

图12 方位历程图(时域干扰阻塞方法)Fig.12 Bearing-time history (interference block in time domain)

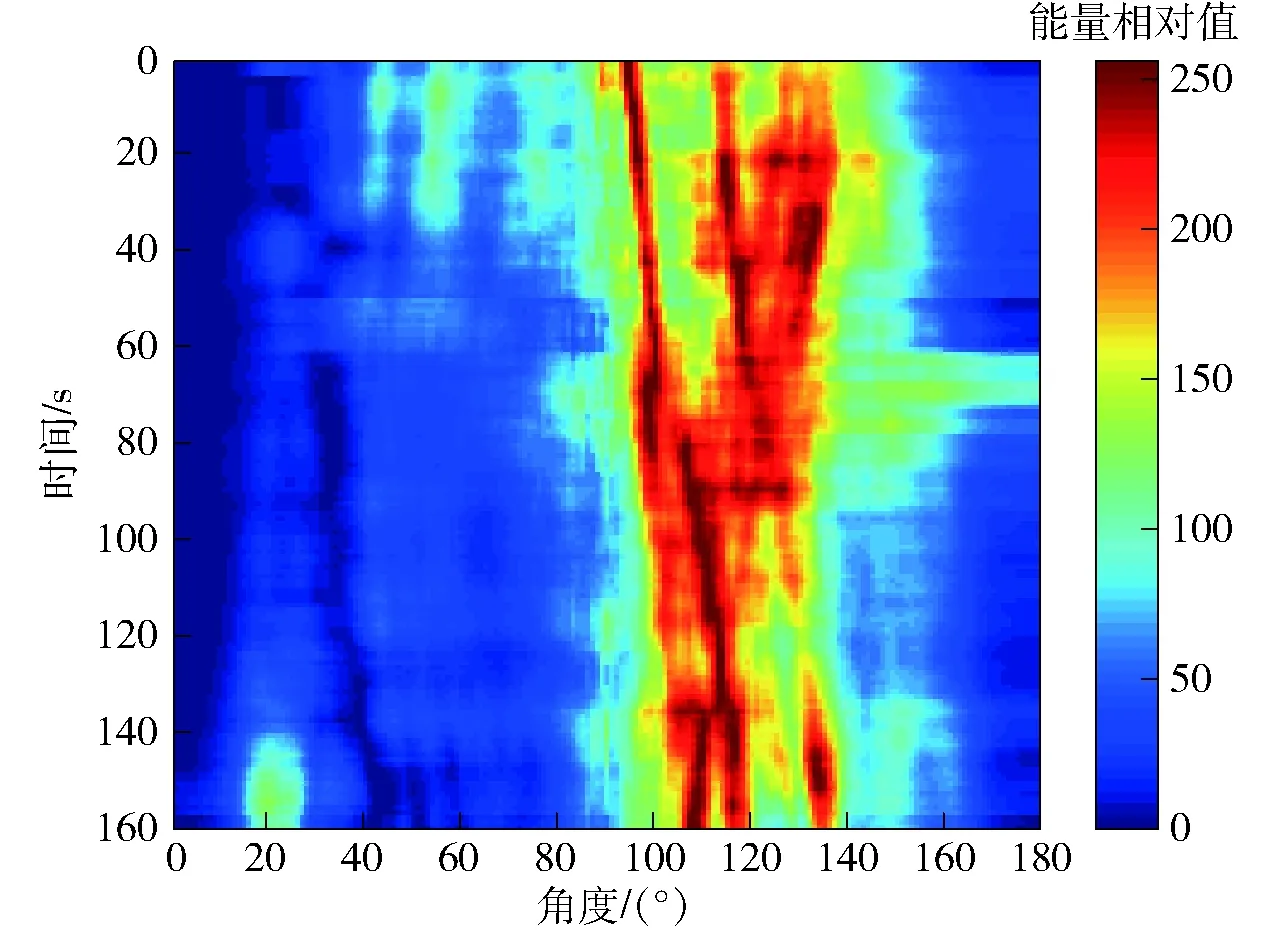
图13 方位历程图(本文方法)Fig.13 Bearing-time history (the proposed method)

由图11～图13可知，在阻塞θ0为20°～40°和θ0=160°附近干扰时，相比时域干扰阻塞方法，本文方法可对120°～140°处运动弱目标实现有效探测。试验数据2处理结果进一步验证了本文方法通过引导信号减小了时域干扰阻塞衰减区间，实现了波束校正，对原衰减区间内的弱目标实现有效探测。

4 结论

1) 本文论述了时域干扰阻塞方法实现原理，分析了时域干扰阻塞前后线列阵波束形成输出信号与噪声能量变化函数，并通过数值仿真验证了波束形成输出信号与噪声能量变化趋势一致性。根据理论和数值仿真分析结果，提出了基于引导信号修正的时域干扰阻塞方法，修正方法通过模拟噪声能量变化趋势，减小了时域干扰阻塞方法对线列阵波束形成输出信号能量造成的衰减区间，实现了波束校正。

2) 在仿真条件下，相比时域干扰阻塞方法，本文方法未成功检测目标(成功概率小于50%)对应方位区间宽度由40°缩小到5°. 数值仿真和海试数据处理结果进一步验证，本文方法利用引导信号形成的衰减曲线对输出波束进行非线性化处理，有效地缩小了线列阵波束形成输出信号能量差异，降低了原时域干扰阻塞方法对衰减方位区间内目标探测性能影响，提高了时域干扰阻塞方法抗干扰性能和探测性能，为进一步提高时域干扰阻塞方法的性能提供了一种可行方案。