复杂约束条件下伴随修理任务多目标动态调度
2019-04-17刘彦陈春良昝翔陈伟龙张立君
刘彦, 陈春良, 昝翔, 陈伟龙, 张立君
(陆军装甲兵学院 装备保障与再制造系, 北京 100072)
0 引言
信息化条件下的现代战争突显出作战节奏快、战场空间广、保障任务重等特点,对战时装备维修的实效性提出了更高的要求。伴随修理作为战时装备维修的主要修理方式之一,将修理力量编成伴随修理组实施伴随保障,可使战损或故障装备尽快参与战斗,是快速保持和恢复作战部队战斗力的重要手段。
面对战时不断随机出现的修理任务,保障指挥员如何根据作战任务需求,在有限的维修时间内综合考虑待修装备的维修工作量、维修优先级等因素,以及伴随修理组的修理能力及其变化、转场时间等因素,科学合理地确定伴随修理的修理任务及修理顺序,使维修效益达到全局最优化,是战时装备维修保障亟待解决的关键问题。
由于战场态势复杂,战时装备维修任务调度方面的研究约束条件多、研究难度大,但众多学者对装备维修任务调度进行了深入探索,取得了一定成果,具有一定的指导意义。文献[1]以尽快恢复装备战斗力为目标,分析了动态维修任务调度的优化方法。文献[2]考虑时间约束及负载能力约束的影响,将装备维修任务调度问题转化为车辆路径问题(VRP),并设计了基于改进最大- 最小蚂蚁系统(MMAS)的维修任务规划方法,实现单修理组的维修任务调度。文献[3]提出了进攻作战抢修任务动态调度问题,将其抽象为动态车辆路径问题,以获得的二次作战时间最大为调度目标构造了调度模型,并设计了变体遗传算法(GA)进行模型求解。文献[4]考虑修复时间不确定性以及抢修组转场时间不确定性,构建了机动作战抢修任务调度模型,并通过示例验证了模型和算法的可行性。
目前,装备维修任务调度目标主要集中在最大保障时间[5]、修竣装备重要度之和最大[6]、获得的二次作战时间最大[3]等,不同调度目标的侧重点不同,但多目标优化是维修任务调度的趋势。根据修理方式特点抽象出的装备维修任务调度问题主要有资源约束项目调度问题[7]和VRP[8-9],其中:资源约束项目调度模型适用于基地级修理或定点修理;VRP适用于伴随修理和巡回修理,运用也更加广泛。约束条件方面,现有装备维修任务调度研究在VRP基础上根据战场情况进行了延伸,主要聚焦于随机需求[10]、时间不确定性[11]等传统约束,文献[7]考虑到维修资源周期性工作问题,提出了考虑休息的维修任务调度模型;文献[12]考虑到战场抢修时的修理能力限制,提出了非遍历型调度,符合战时修理实际,具有一定的指导意义。然而时间窗[13-14]等其他约束在装备维修任务调度中的研究较少且不够深入,有待进一步完善对战场其他现实约束的考虑,以使得维修任务调度更加合理可靠。
综上所述,现阶段伴随修理装备维修任务调度的研究存在以下3个问题:
1)现有研究针对的背景和问题不完全相同,未深入分析伴随修理背景下如何基于诸多实际约束来合理地规划伴随修理组维修任务以及动态处理不确定性信息,缺乏对伴随修理装备维修任务调度这一现实军事问题的模型化描述和深入研究。
2)现有研究多以最大保障时间、最长二次作战时间等作为单一的调度目标进行任务调度,可能难以全面反映战时伴随修理的维修任务调度需求,需要加强复杂战场环境下决策者对其他调度目标的考虑,从多个目标出发,以更有利于寻求全局最优化。
3)没有充分考虑复杂约束对装备维修任务调度的影响。装备维修任务调度问题作为复杂优化问题,具有诸多现实约束,而现有的研究较少考虑约束问题,模型过于理想化,降低了调度模型的适用性和合理性。由于待修装备修理时间窗、非遍历性、修复状态的不确定性以及修理能力的变化等约束客观存在,会对维修任务调度产生重要影响,因此需要在调度过程中深入分析,以使得维修任务调度模型更加符合战场实际。
本文针对以上问题,以伴随修理维修任务调度这一复杂军事难题为研究对象,引入修理时间窗约束和非遍历性约束,考虑修复状态不确定性和修理能力的变化对调度的影响,以修复装备数量、修复装备重要度以及获得的二次作战时间为多维调度目标,构建伴随修理的维修任务多目标动态调度模型,根据模型特点设计改进的GA进行求解,并通过示例验证模型的科学性和合理性。
1 基本描述
1.1 问题描述
在现代战争中,随着作战进程的推进以及作战任务的逐行,在敌方火力打击下,我方作战装备不可避免地会在不同时间、不同地点出现不同程度的损伤。为及时抢修分布在战场上的众多受损装备,我方伴随修理力量编成伴随修理组展开伴随保障。在实施伴随保障过程中,为充分利用现有维修资源应对不断出现的维修任务,需要对维修任务进行动态调度。在调度过程中,各待修装备的位置、预计修理时间和修复到不同状态的装备重要度等信息,在一体化指挥信息平台的支撑下已通过相应的手段获知,且各待修装备均希望在其对应的时间窗内得到修复,否则将会影响其修复后继续参战的重要度。在伴随修理过程中,保障指挥员会根据不断更新的待修装备及伴随修理组信息,对伴随修理组的修理计划进行动态调度。
在待修装备不断出现而修理时间和修理能力有限的前提下,为使得伴随修理效果实现全局的最优化,亟需为伴随修理组分配合适的待修装备,并确定各待修装备之间的修理顺序及修复状态,还需要根据不断出现的待修装备对维修任务进行动态调整,以使得作战部队战斗力得到最及时有效的恢复,即为本文研究的伴随修理装备维修任务调度问题。
1.2 假设描述
为了简化问题,突出重点,做出如下假设:
1)参与维修任务调度的各待修装备均在伴随修理组的修理能力范围内;
2)研究对象为营伴随修理力量,编成一个伴随修理组,对所属保障对象开展伴随修理;
3)维修任务调度前,各待修装备的位置、预计修理时间、装备重要度、修理时间窗等信息均已通过技术侦察获知;
4)伴随修理组从初始位置出发,前往待修装备地域对其进行伴随修理,完成修理任务后不返回初始出发点,而是等待保障指挥员下达新的维修任务指示;
5)待修装备修复后直接归建作战部队参与作战,忽略归建时间。
6)伴随修理组修理过程中不会由于任务调整而中止当前任务。
2 模型构建
2.1 条件假设
为了方便对模型进行描述,引入以下符号体系及条件假设:
1)战斗开始时刻为0 min,伴随修理开始时刻为Ts,战斗结束时刻为Te.
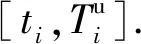
3)待修装备修复至能正常作战为S1,修复至能应急作战为S2,待修装备i修复至第p(p=1,2)种状态的装备重要度为δi,p,相应的预期维修时间分别为Ti,S1、Ti,S2.
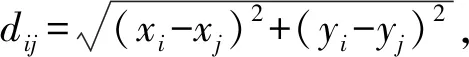
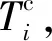
6)引入0~1变量τi,当待修装备i得到修复时τi=1,否则τi=0.
7)随着修理任务的开展,势必导致修理人员疲劳,从而影响修理效率,记修理效率为ξk,表示执行第k(k={1,2,…})次修理任务时的修理效率,修理效率随修理任务的实施不断下降。
8)记O={o1,o2,…,ol}(l为截点,l≤n)为该问题的一个可行解,表示一个可行的规划路径,即修理组开展伴随修理的装备编号序列,ol为截点装备;|O|表示该可行解中包含的元素个数,即该规划路径中的装备数;om表示该规划路径中的第m(m={1,2,…,l})台装备。
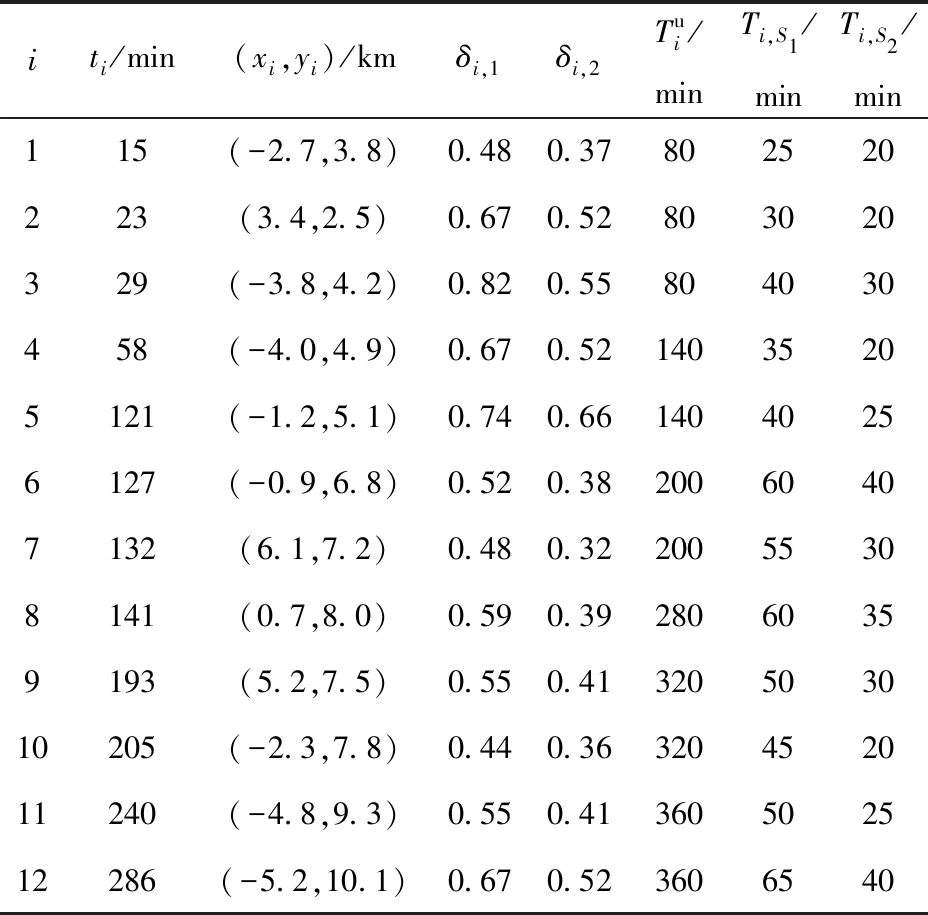
9)将可行解O={o1,o2,…,ol}补充为完整修理任务规划O′={o1,o2,…,ol,ol+1,…,on},有Tol≤Te 战时伴随修理的目的在于在各种限制条件下尽最大可能修复待修装备,使其尽快返回战场继续参与战斗,以发挥修竣装备对装备体系的贡献,使作战部队战斗力得到最大限度的恢复。为全面衡量维修任务计划安排的优劣,用以下3个参数对维修任务调度优劣进行量化度量: 1)修竣装备总数F1. 修竣装备总数是整个战斗过程中伴随修理组修复的待修装备数量总和,反映了战时伴随修理力量在给定时间域内逐行修理任务的快慢程度,直接影响了装备参战率。对于遍历型修理,待修装备得到全部修复,此时F1即为待修装备总数;对于非遍历型修理,待修装备并非全部得到修理,F1是保障指挥员最看重的因素之一。 2)修竣装备总重要度F2. 修竣装备重要度反映地是所修竣装备对整个装备体系的贡献程度,是修竣装备重要度的总和。重要度越高的装备对装备体系及整个战斗的影响越大,也是待修装备的优先级反映。 3)获得的二次作战总时间F3. 二次作战时间总时间是指伴随修理组修竣的待修装备二次作战时间的代数和。二次作战时间是指战斗持续进程中,修竣装备从修竣时刻至战斗结束时刻的时间长度,反映了待修装备得到及时修复的程度以及修竣后装备发挥有效作用的时长,是修理及时程度的体现。修理越及时,待修装备修竣后返回战场所参加的二次作战时间越长,对本次战斗的贡献就越大,相应的伴随修理也就越有意义。 以上三者相互制约、相互影响,难以同时达到最优,因此需要构建维修任务调度的多目标优化模型,以实现全局的最优化。 2.3.1 修理时间窗分析 对于战时伴随修理,各待修装备均希望尽快得到修复、返回战场继续完成任务,然而受修理能力的限制,并不能实现各待修装备在第一时间均得到修复。随着时间的推移,由于作战阶段、作战任务的改变,当超过某一时刻待修装备仍未得到修复时,待修装备的重要程度就会受到影响。因此本文引入待修装备修理时间窗概念对这一现实问题进行刻画,对超出修理时间窗而未得到修复的待修装备重要度进行惩罚,具体惩罚公式如下: (1) 式中:ηi,p为经时间窗惩罚后待修装备i修复至第p种状态的装备重要度。 2.3.2 非遍历分析 非遍历是指沿某一搜索路径对集合中的部分元素做一次且仅做一次访问,被访问元素具有不确定性。与传统维修任务分配不同,战时伴随修理由于时间紧、任务重,难以对散布在战场的各待修装备实现全部修复,即伴随修理组只能完成部分维修任务,属于非遍历任务调度。非遍历性描述的是各待修装备是否均得到修复,其对调度模型的影响通过待修装备修竣时刻的时间约束实现。对于遍历型维修任务的动态调度,其相关约束为Tok≤Te,∀k,k≤|ol|,而非遍历维修任务调度对约束条件松弛为Tok≤Te 2.3.3 修理能力分析 战时伴随修理的修理环境恶劣,受战场环境等诸多因素影响,修理能力并非固定值,而是会不断发生变化,具有不确定性。随着修理任务的实施,势必会造成修理人员的疲劳,从而影响修理效率,使修理能力发生变化。为解决修理人员疲劳带来的修理能力变化问题,本文引入修理效率概念,确定每次修理任务的完成对修理效率的影响,从而确定修理能力的变化,修理效率计算公式为 ξk=βξk-1, (2) 式中:ξk为执行第k(k≥2)次修理任务时的修理效率,ξ1=1;β为修理效率衰减系数。 由上述分析可以看出,修理能力对待修装备的影响还可以通过修理顺序的不同来实现,即待修装备的修理时间会由于修理顺序的不同而受到修理效率的影响,从而使得装备维修任务调度更为复杂。 2.3.4 修复状态分析 伴随修理的目的是在规定时间域内修复战损或故障装备或恢复其部分功能,使其尽快返回战场参战。考虑到战时修理任务的时效性,待修装备的修复状态具有不确定性,从而使维修任务调度更复杂,求解难度更大。 从装备完成任务的角度分析,有效的伴随修理应使修竣装备能够正常作战或应急作战,因此待修装备的修复状态可以分为能正常作战S1和能应急作战S2两类,将待修装备恢复至不同状态一方面所需的修理时间明显不同,另一方面获得的装备重要度也有所差异,因此会对维修任务调度产生较大影响。通过引入待修装备修复状态这一现实约束,可以使维修任务调度更加贴合实际,也更具有实用性。 在分析伴随修理装备维修任务调度目标的基础上,结合伴随修理特点及相关现实约束,构建装备维修任务调度模型。 目标函数: maxF=max (F1,F2,F3), (3) (4) (5) (6) 约束条件: (7) (8) (9) (10) (11) (3)式表示面向伴随修理的装备维修任务调度目标是修竣装备总数最大、修竣装备总重要度最大、获得的二次作战总时间最多;(4)式、(5)式、(6)式分别表示3个目标参数;(7)式表示伴随修理组从初始位置出发前往修竣第1台待修装备的时间关系;(8)式表示伴随修理组修理可行解中相邻两待修装备的修竣时刻的约束关系;(9)式表示修理时间以及修理能力的约束关系;(10)式表示伴随修理组在战斗结束之间进行的修理才有效,反映了非遍历约束关系;(11)式表示对装备是否修复做0~1约束。 1)多目标分析。不同于传统维修任务调度单纯追求某一目标而导致调度方案在其他需求方面存在较大偏离,本文所构建的装备维修任务调度模型通过修理数量、修理对象重要程度和修理及时性3个方面权衡维修任务调度方案的优劣,在多个目标中协调平衡,获得一组可接受解(即Pareto最优解集[15]),增加了保障指挥员的决策余地,可以根据战场实际需求和决策者偏好从Pareto最优解集中选择合理的调度方案。 2)动态驱动策略分析。装备维修任务动态调度的实质是根据调度需求进行多次维修任务调度的过程。而动态驱动策略就是设定某一驱动条件,用以判断该时刻是否需要对维修任务进行再次调度。因此,动态驱动策略是动态调度的基础。 结合伴随修理特点,本文设定面向伴随修理的装备维修任务动态调度动态驱动策略为:伴随修理组每修复一台装备且有新的待修装备出现时,便根据该时刻时间点、伴随修理组位置信息、待修装备信息(包括新出现的待修装备信息)进行一次重调度,并将该修竣装备记为关键点,将该时刻记为重调度时刻。该动态驱动策略可以消除待修装备的实际修理时间与计划修理时间差异所导致的调度误差,通过每次重调度前的信息更新实现动态调度的可靠性。 由第2节分析可知,伴随修理装备维修任务调度问题是多约束条件下的多目标动态调度问题,下面针对其特点,设计改进GA进行模型求解。 传统多目标优化方法如权重系数法、目标规划法和约束法等,通过将多目标问题转化为1个或一系列单目标优化问题进行求解,存在依赖先验知识、难以处理Pareto最优前端非凸等问题。而带精英策略的非支配排序遗传算法(NSGA-Ⅱ)作为最优秀的多目标进化算法之一,在保证种群多样性和保护种群优良个体的同时降低了计算复杂度[16]。因此,本文通过NSGA-Ⅱ算法的精英策略,采用非支配排序方法并结合拥挤度比较算子,获得多个Pareto最优解,从而为保障指挥员提供决策依据。保障指挥员可根据战场态势和实际需求,依托决策偏好和决策策略,在Pareto最优解集中选择最满意解。 设定决策策略为:通过对Pareto最优解集中的解进行规范化处理,采用加权法进行排序优选,从而选择满意解: (12) 为实现伴随修理装备维修任务调度的非遍历约束,设计两段式编码:前段采用顺序编码,用以表示伴随修理组的修理顺序;后段采用1~2整数编码,用以表示待修装备的修复状态,1表示修复状态为S1,2表示修复状态为S2. 该编码方式能实现非遍历约束及修复状态约束,且染色体与解一一对应,避免了遗传操作中不可行解的产生,大大提高了算法收敛速度。选取目标函数作为适应度函数,通过相关约束求得截点的信息和相应适应值,从而实现解码。 编码和解码示例分别如图1、图2所示,染色体为X=(4,8,2,6,3,1,7,5,1,1,2,1,2,2,1,2,5),n=8,根据所求得的截点信息实现解码,其含义为:受相关约束影响,对8台待修装备中的5台进行了修理,伴随修理组的任务安排及修理顺序为(4,8,2,6,3),修复状态为(S1,S1,S2,S1,S2,S2,S1,S2),适应值分别为F1(t)、F2(t)、F3(t). 图1 编码示例Fig.1 Encoding example 图2 解码示例Fig.2 Decoding example 3.3.1 选择 染色体选择采用Binary Tournament Selection,并根据比较算子(由NSGA-II计算非支配排序和个体间拥挤距离得到)从上一代染色体中选取20%的个体作为父染色体,进行后续交叉变异操作。 3.3.2 交叉变异 由于染色体采取两段式编码,各段编码方式以及对应的实际意义不同,其交叉变异无法直接采用传统交叉变异方式进行。为了增大搜索范围、提高收敛速度,针对编码特点,确定“前段仅进行变异操作,后段可进行交叉及变异操作”的思路,设计混合策略遗传算子如下:1)前段和后段均采用随机更新操作;2)前段采取随机更新,后段采取倒置操作;3)前段采用倒置操作,后段采用随机更新操作;4)前段采用倒置操作,后段采用滑动平移操作;5)前段不采取操作,后段采用随机更新操作。 模型求解算法的流程如下: 步骤1初始化相关参数(种群规模pop_size、最大迭代次数num_gen等)。 步骤2随机产生初始种群P0. 步骤3对种群P0中任一染色体进行解码,计算其适应值和截点信息Cl,得到初始化可行解种群O,记为pop_chrom. 步骤4由NSGA-II对可行解种群O进行快速非支配排序,计算非支配集个体间拥挤距离。 步骤5令gen=1. 步骤6根据Binary Tournament Selection,从pop_chrom中随机选出数量规模为pool_size的父代染色体种群parent_chrom. 步骤7采用混合策略遗传算子进行遗传操作,产生子代染色体种群offspring_chrom. 步骤8计算offspring_chrom中任一染色体的截点信息及其适应值。 步骤9采用NSGA-II算法对pop_chrom及offspring_chrom进行快速非支配排序,计算非支配集个体间拥挤距离。 步骤10根据Binary Tournament Selection,从pop_chrom及offspring_chrom中筛选出规模为pop_size的基因较优新一代染色体pop_chrom,从而实现父代优秀个体基因的精英保留。 步骤11判断gen 步骤12令gen=gen+1,转步骤6,继续寻优。 步骤13停止迭代,获得本次维修任务调度的Pareto最优解集,依据决策策略从中计算出F′,转步骤14. 步骤14判断重调度驱动策略是否满足?若满足则转步骤1进行重调度,否则转步骤15. 步骤15运算终止,输出调度结果。 某合成营受上级指示执行机动进攻作战任务,受故障和敌方火力打击,陆续出现待修装备,该营配属一个伴随修理组对所属部队逐行伴随修理任务,负责修理120 min内能完成的待修装备,在一体化指挥信息平台的支撑下,各待修装备相关信息已知。而随着进攻作战的持续,待修装备不断出现,保障指挥员需要为伴随修理组分配合适的待修装备,确定各待修装备之间的修理顺序及修复状态,并根据不断出现的待修装备对维修任务进行动态调整。 战斗初期(t≤200 min),需要更多更重要的装备及时参战,取μ1=0.1,μ2=0.6,μ3=0.3;战斗后期(t>200 min),需要提供更多的作战时间,取μ1=0.2,μ2=0.3,μ3=0.5. 根据伴随修理组实际机动时间、实际修理时间以及调度策略对装备维修任务进行调度,得到调度规划结果如表2所示。 此次伴随修理装备维修任务调度共经历了5次调度过程,在MATLAB软件平台用时分别为12.05 s、11.97 s、12.08 s、13.21 s、14.01 s. 最终维修方案的规划路径如图3所示。 根据分析以上示例仿真结果,可以得到以下结论: 表1 待修装备信息 1)从伴随修理组开始实施伴随修理至战斗结束,修理任务的路径规划为2-1-4-3-5-10-11-9,共修复装备8台,获得的装备重要度总和为3.94,获得的二次作战时间为1 392 min,在很大程度上恢复了部队战斗力,间接证明了战时伴随修理的重要性。 2)调度时间均在15 s以内,满足战时装备维修任务调度的实效性要求,同时也证明了所构模型和算法的可行性。 3)受动态驱动策略的影响,一共进行了5次调度,实现了待修装备不断出现情况下的维修任务动态调整。其中,前3次调度属于遍历型调度,后2次调度属于非遍历型调度;待修装备6、7、8、12未纳入最终的伴随修理装备维修任务规划中,这主要是因为战时修理时间的限制导致修理任务无法全部完成,反映了伴随修理的非遍历性。 表2 调度规划结果 图3 伴随修理装备维修路径规划图Fig.3 Equipment repair route plan with accompanying repair 4)规划路径中出现了折线1-4-3,这是因为在时刻67 min进行第2次调度时,参与调度的装备是1、3、4,而待修装备3相对于待修装备4的重要度低且修理时间长,因此伴随修理组修完待修装备1后,舍弃较近的待修装备3,而先修理重要度高且更易修复的待修装备4,能够满足战时修理时“先修重要装备”以及“先修易修装备”的要求,也从侧面反映了调度模型的合理性。 5)前2次调度,待修装备的修复状态均为S1,这是因为前期待修装备较少,预计的修理时间相对充裕,而μ2取值较大,将装备修复至S1状态能获得更多的重要度,且前期修竣装备参战时间相对较长,更高的重要度有利于发挥作战效能。后3次调度,待修装备的修复状态多为S2,因为此时参与调度的待修装备数量多,且在战斗后期,μ3取值较大,希望能获得更多装备二次作战时间,因此将待修装备修复至S2状态既能节约修理时间以完成更多修理任务,又能迅速使其返回战场以获得更多的二次作战时间。 本文提出了伴随修理装备维修任务动态调度军事问题,构建了复杂约束条件下的伴随修理多目标动态调度模型,设计了相关求解算法,并通过示例验证了该模型及算法的合理性。本文所构建的模型更加符合复杂约束这一战场实际,为伴随修理装备维修任务调度难题提供了模型及方法参考,为战时保障指挥员维修决策提供了数学支撑。 下一步将对巡回修理中多巡回修理组的装备维修任务动态调度问题展开研究。2.2 多目标参数分析
2.3 约束条件分析
2.4 调度模型建立
2.5 调度模型分析
3 模型求解
3.1 Pareto最优解集构建

3.2 编码与解码设计


3.3 遗传算子设计
3.4 算法流程设计
4 示例仿真与分析
4.1 示例仿真
4.2 结果分析

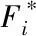

5 结论
