地面重力条件模拟月面载人月球车直线加速的驱动算法

梁忠超， 王永富

(东北大学 机械工程与自动化学院， 辽宁 沈阳 110819)

0 引言

月球具有丰富的空间资源和矿物资源，探测和研究月球是人类深化了解地球、太阳系以及宇宙起源的最佳途径，目前月球已成为国内外众多研究学者的研究对象[1-2]。随着月球探测深度和广度需求不断增长，月面探测方式已经逐渐开始从无人月面探测向载人月面探测转变，不断寻求并实现更多种类的月面探索任务[3]。

载人月球车是载人月面探测任务中必不可少的探测工具之一[4]。载人月球车可以提高宇航员执行任务的效率、扩大探测月面的范围、缩短探测时间。同时，由于月面地形环境复杂、恶劣，并覆盖着松软的月面土壤[5]，驾驶载人月球车的宇航员须具有较高驾驶技术。原因在于：当宇航员驾驶载人月球车行驶于月面时，车轮容易打滑[6]，从而也使得轮—地接触特性变得更为复杂[7]。因此，宇航员登陆月面之前需在地面条件下展开相关模拟实验和驾驶训练。

在地面条件下，进行模拟月面载人月球车行驶实验时，由于地面重力加速度是月面重力加速度的6倍，当直接使用质量相同的地面模拟车进行模拟实验时，会产生6倍整车垂直载荷的差异；当使用垂直载荷相同的地面模拟车进行模拟实验时，会产生1/6整车质量的差异。无论整车垂直载荷还是整车质量差异都会导致相同驾驶操纵输入却产生完全不同的地面模拟车与载人月球车的操纵差异。

目前，在地面条件下，采用较多的模拟月面条件方法主要包括质量等效法[8]和悬挂重力补偿法[9-11]。质量等效法是去除载人月球车上部分探测工具，从而获得等效1/6整车质量的方式去模拟与月面载人月球车相同的垂直载荷。但由于存在质量差异，相同牵引力会产生6倍的加速度差异，质量等效法多用于较低速度运动的无人星球探测车。悬挂重力补偿法是使用悬挂补偿系统，使用吊绳悬挂并补偿月球车5/6的重力方式进行模拟。悬挂重力补偿法通常会受到场地和悬挂补偿系统的限制。针对上述问题，使用地面模拟车对月面载人月球车直线加速行驶进行模拟时，可采用模拟控制器分别对直线加速和转向运动进行模拟，并补偿由于重力差异所带来的操纵差异。本文对月面载人月球车直线加速行驶的地面模拟进行了研究，建立了月面载人月球车的整车直线加速模型，推导了基于地面力学理论和被动滑转原理的模拟算法，并最终通过改变车轮驱动力矩的方式实现了地面模拟车对月面载人月球车直线加速行驶的模拟。

1 载人月球车直线加速模型

1.1 单个车轮的直线运动力学模型

根据Bekker土壤承压模型，车轮下方受到土壤的法向平均正压力[7]为

σ=(kc/b+kφ)zn，

(1)

式中：kc为土壤内聚力变形模量(kPa/mn-1)；n为沉陷指数；b为车轮宽度(m)；kφ为土壤摩擦变形模量(kPa/mn-1)；z为车轮下陷量(m)。

根据Janosi土壤剪切模型，车轮下方受到土壤的切向剪切应力[7]为

(2)

式中：c为土壤内聚力(kPa)；φ为土壤内摩擦角(°)；j0为土壤剪切变形模量(mm)；j为土壤的剪切变形量(mm)，且

j=r[(θa-θ)-(1-s)(sinθa-sinθ)]，

(3)

r为车轮半径(m)，θa为车轮进入角(°)，θ为车轮与土壤接触夹角(°)，s为车轮滑转率。

定义车轮牵引力为FDP，车轮牵引力与车轮驱动扭矩之间关系为

(4)

式中：T为车轮驱动扭矩(N·m)；TRC为车轮压缩土壤时所受阻力矩(N·m)。由(4)式可知，车轮驱动扭矩克服了由于压缩土壤阻力矩后所产生了牵引力，只有当T>TRC时车轮才可能产生直线加速度。

车轮在行进过程中，由于滑转现象的产生，车轮正压力分布峰值并不在其正下方，而是会产生一定偏移角度[10]

θm=(c1+c2s)θa，

(5)

式中：c1和c2为最大正应力角系数。

因此，根据Wong-Reece正应力分布模型[11]，车轮正压应力和剪切应力可由(6)式和(7)式求出：

式中：θd为车轮离去角(°)。

根据应力分布可得车轮垂直载荷、牵引力、驱动力矩的计算公式。根据被动滑转原理[12]可得

W(s,θa)=br(σ2(θ)cosθ+τ2(θ)sinθ)dθ+

(8)

FDP(s,θa)=
br(τ2(θ)cosθ-σ2(θ)sinθ)dθ+

(9)

(10)

1.2 整车力矩驱动的直线加速模型

月面载人月球车进行直线加速行驶时，4个车轮的总牵引力是直接影响其直线加速或减速行驶速度的参数。同时，通过(8)式～(10)式可知，影响整车总牵引力的参数还包括整车质量、质心位置、车轮驱动力矩、土壤参数等。载人月球车为左右对称结构，故仅对其单侧车轮进行受力分析，如图1所示。其中：Wv为整车垂直载荷(N)；Wf为前轮垂直载荷(N)；Wr为后轮垂直载荷(N)；FDPv为整车牵引力(N)；FDPf为前轮牵引力(N)；FDPr为后轮牵引力(N)；lf为质心与前轮间的距离(m)；lr为质心与后轮间的距离(m)。

根据被动滑转原理[13]，当已知土壤参数时，可将(8)式～(10)式转化为θa和s的函数方程。因此，前轮垂直载荷Wf、前轮牵引力FDPf、前轮驱动力矩Tf可由前轮滑转率sf和前轮进入角θaf的函数表示。同样，后轮垂直载荷Wr、后轮牵引力FDPr、后轮驱动力矩Tr可由后轮滑转率sr和后轮进入角θar的函数表示。

由于前轮和后轮被车体刚性连接，因此前轮和后轮受力模型是相互耦合的，载人月球车单侧车轮垂直载荷应为整车垂直载荷的1/2，即

Wf+Wr=mg/2，

(11)

式中：m为载人月球车整车质量(kg)；g为重力加速度(m/s2)。

定义载人月球车的质心位置参数为

iG=lr/(lf+lr)，

(12)

式中：iG为载人月球车的物理参数，是不随重力而改变的定值，该值可较容易测得。因此，通过iG和m可获得前轮垂直载荷和后轮垂直载荷分别为

(13)

载人月球车单侧车轮牵引力应为整车牵引力的1/2，即

(14)

式中：a为月面载人月球车整车直线加速度(m/s2)。

载人月球车采用车轮扭矩驱动的操纵控制方法时，4个车轮采用相同的驱动力矩T，宇航员加速操纵转角输入为uA，T与uA关系为

T=ituA，

(15)

式中：it为载人月球车的扭矩操纵比例系数(N·m/rad)。

月面载人月球车行驶时，宇航员给出操纵输入，前轮和后轮受到相应驱动力矩驱动，将(13)式和(15)式带入(8)式和(10)式中，可获得前轮牵引力和后轮牵引力，将其带入(14)式可得到载人月球车整车牵引力和整车直线加速度。因此，月面载人月球车的直线加速度不仅与车轮驱动力矩有关，同时还受到整车载荷的影响。

2 直线加速模拟算法

2.1 直线加速度差异分析

通过相同质量和相同垂直载荷两种方式进行对比模拟。

2.1.1 相同质量

令月面载人月球车与地面模拟车具有相同质量，即

mL=mE，

(16)

式中：mL和mE分别为月面载人月球车和地面模拟车的整车质量(kg)。

月面重力加速度为地面重力加速度的1/6，即

(17)

式中：gL和gE分别为月面和地面的重力加速度(m/s2)。

将(16)式和(17)式带入(13)式可得

(18)

由于月面载人月球车整车垂直载荷远小于地面模拟车整车垂直载荷，根据被动滑转原理可知，相同驱动力矩无法使车轮在月面和地面产生相同的牵引力。通过(14)式可知，月面载人月球车与地面模拟车具有相同质量时，由于整车牵引力不同，无法产生相同的直线加速度。

2.1.2 相同垂直载荷

令月面载人月球车与地面模拟车具有相同垂直载荷，即

(19)

当月面载人月球车与地面模拟车具有相同垂直载荷并使用相同驱动力矩时，月面载人月球车和地面模拟车可以获得相同的牵引力。此时，月面载人月球车和地面模拟车使用相同驱动力矩时可以获得相同的整车牵引力。

将(19)式带入(13)式可得

mL=6mE.

(20)

由(20)式可见，相同垂直载荷条件下，月面载人月球车整车质量为地面模拟车整车质量的6倍。将(20)式、月面载人月球车和地面模拟车相同的整车牵引力带入(14)式可得

(21)

式中：aL和aE分别为月面载人月球车直线加速度和地面模拟车直线加速度(m/s2)。

由(21)式可知，相同垂直载荷条件下，地面模拟车可获取与月面载人月球车相同的牵引力，但由于质量不同，无法获得相同的直线加速度。

2.2 力矩驱动模拟算法

月面载人月球车采用车轮扭矩操纵方法，4个车轮采用相同的驱动力矩TL，宇航员操纵转角输入为uA，uA与TL关系为

TL=iLuA，

(22)

式中：iL为月面载人月球车操纵比例系数(N·m/rad)。若要地面模拟车获得与月面载人月球车相同的直线加速度，则需要宇航员操纵转角输入始终为uA，并获得aE=aL. 相应地，月面载人月球车和地面模拟车的驱动力矩分别为TL和TE，此时TL≠TE，需要推导模拟算法来获得TL和TE的关系。

当宇航员操纵转角输入已知时，可以通过(22)式得到驱动扭矩TL. 利用和可以得到月面载人月球车前轮和后轮的运动状态方程分别为

(23)

(24)

基于单轮牵引力模型，可以建立月面载人月球车整车直线加速运动的力学模型，则月面载人月球车单侧牵引力为

(25)

若要使地面模拟车产生与月面载人月球车相同的aE，则应有

(26)

定义质量比例系数为

(27)

相同直线加速度条件下，由(26)式和(27)式可得月面载人月球车牵引力与地面模拟车牵引力关系为

(28)

由(28)式可见，为了模拟月面载人月球车的直线加速行驶，地面模拟车需要产生的整车牵引力是月面载人月球车整车牵引力的im倍。

由单轮力学模型(8)式～(10)式可得地面模拟车前轮和后轮的牵引力与垂直载荷关系方程：

(29)

(30)

地面模拟车4个车轮使用相同驱动力矩TE，即

(31)

根据(25)式～(28)式牵引力的求解，联立(29)式～(31)式可得

(32)

式中：

(33)

通过(23)式～(32)式的求解过程可得到地面模拟车获得与月面载人月球车相同直线加速度的模拟算法，求解简图如图2所示。

3 月面模拟算法校验

3.1 月面土壤的物理参数

目前，主要通过返回测定和就位测定两种方法进行真实月面土壤的参数测定。返回测定方法是将在月球表面采集月面土壤，将其带回地面后进行研究和分析，美国和苏联都进行过相应的月面土壤的返回测定[14]。但是返回测定由于采集地点、周围环境、重力因素等因素，在返回地面后月面土壤参数会受到一定影响。就位测定是直接在月面进行月面土壤相关参数的测试。美国阿波罗载人月面探测任务中就进行了月面土壤相关参数的实验[13]。

月面土壤的物理特性较为复杂，其中与载人月球车行驶相关的参数主要包括月面土壤密度、孔隙比和相对密实度。通过阿波罗月面土壤采样分析可知，以上参数主要有如下特点[13]：

1)月面土壤密度：车轮与月面土壤作用主要发生在表层，密度为1.45～1.55 g/cm3.

2)孔隙比：用于评价土壤的密实程度。表层月面土壤孔隙比为1.07 ± 0.07.

3)相对密实度：用于评价土壤的抗剪切能力。采样月面土壤密实度为0.6～0.9.

虽然以上参数可以直接反映月面土壤的物理特性，但无法直接应用于车轮的力学模型。因此，美国麻省理工学院和美国国家航空航天局联合建立了车轮实验台，并进行了车轮半经验模型相关的参数辨识[10]，如表1所示。

表1 月面土壤参数

Tab.1 Parameters of lunar soil

3.2 模拟算法的计算验证

地面模拟车通常采用相同质量和相同载荷两种方式来模拟月面载人月球车的直线加速行驶。与整车质量1 200 kg的月面载人月球车对应的相同质量和相同载荷的地面模拟车参数如表2所示。

表2 整车质量与垂直载荷

Tab.2 Mass and vertical load of entire rover

当月面载人月球车与地面模拟车具有相同整车质量时，由于月面重力是地面重力的1/6，相应地，月面载人月球车垂直载荷是地面模拟车垂直载荷的1/6. 如果不使用模拟算法，对月面载人月球车和地面模拟车使用相同的操纵转角输入、车轮驱动力矩，通过(8)式～(10)式计算可得到前轮牵引力和后轮牵引力，此时得到地面非模拟状态的前轮和后轮牵扯引力分别为和相应的车轮扭矩为如图3(a)～图3(c)所示。由图3(a)可以看出，当车轮驱动力矩小于20 N·m时，前轮牵引力和后轮牵引力计算结果小于0 N. 结合(4)式可知，前轮牵引力和后轮牵引力计算结果出现负值的原因在于此时车轮驱动力矩无法克服土壤的压土阻力矩，所得负值牵引力为剩余土壤的压土阻力。当驱动力矩大于20 N·m时，前轮牵引力和后轮牵引力由0 N开始增加。对比图3(c)非模拟状态的地面模拟车前轮牵引力和后轮牵引力，相同驱动力矩条件下，由于地面模拟车垂直载荷是月面载人月球车垂直载荷的6倍，需要克服更大的压土阻力。因此，此时计算得到前轮牵引力和后轮牵引力始终没有克服土壤的前进阻力，计算结果始终为负值。

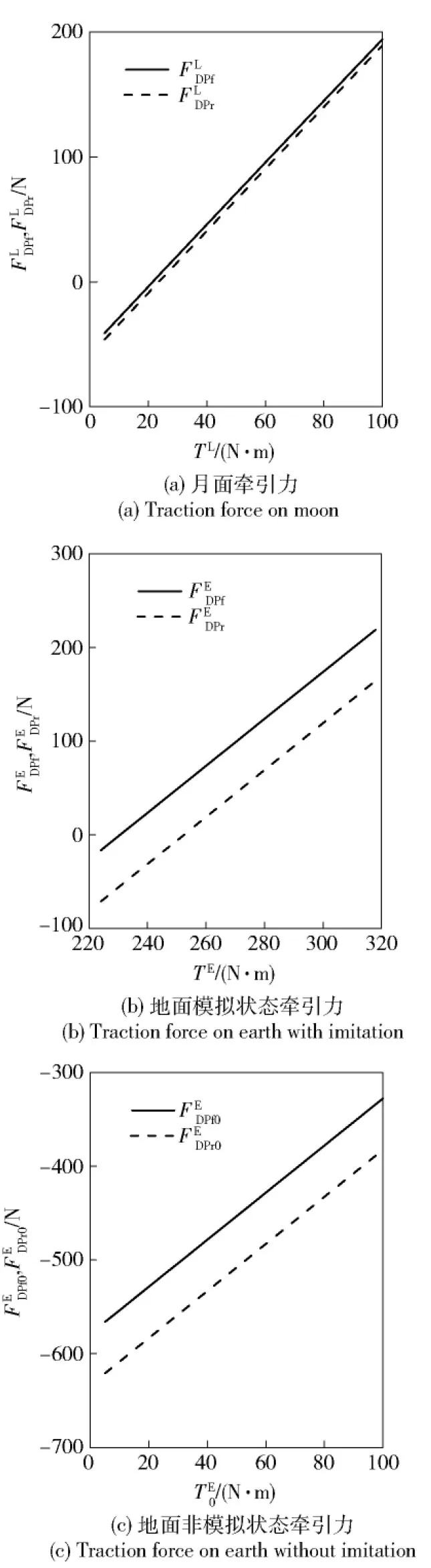
通过(28)式可知，相同质量的地面模拟车与月面载人月球车只有产生相同的整车牵引力才能具有相同的直线加速度。地面模拟车与月面载人月球车直线加速度相同时，采用图2的模拟驱动算法对地面模拟车前轮和后轮进行计算，可得到与图3(a)相应的前轮牵引力和后轮牵引力，如图3(b)所示。由图3(b)可见，地面模拟车垂直载荷是月面载人月球车垂直载荷的6倍，需要更大的车轮驱动力矩。为了分析整车牵引力与加速度，定义整车牵引力公式：

(34)

相同垂直载荷条件下，地面模拟车模拟月面载人月球车的直线加速行驶时，由于重力原因，地面模拟车质量为月面载人月球车质量的1/6，要产生相同的直线加速度，地面模拟车整车牵引力应为月面载人月球车整车牵引力的1/6. 如图5所示月面载人月球车与地面模拟车的前轮牵引力和后轮牵引力的求解。对比图5(a)与图5(c)的计算结果可知：若不使用模拟驱动算法，对月面载人月球车与地面模拟车使用相同的驱动力矩，由于二者垂直载荷相同，月面载人月球车与地面模拟车能够产生完全相同的牵引力，但由于二者质量不同，并不满足产生相同直线加速度的条件；若使用模拟算法驱动的地面模拟车，月面载人月球车与地面模拟车垂直载荷相同时，地面模拟车质量为月面载人月球车质量的1/6，地面模拟车能够产生与月面载人月球车整车牵引力1/6的牵引力关系，此时所需的前轮和后轮驱动力矩也相应降低，如图5(b)所示。

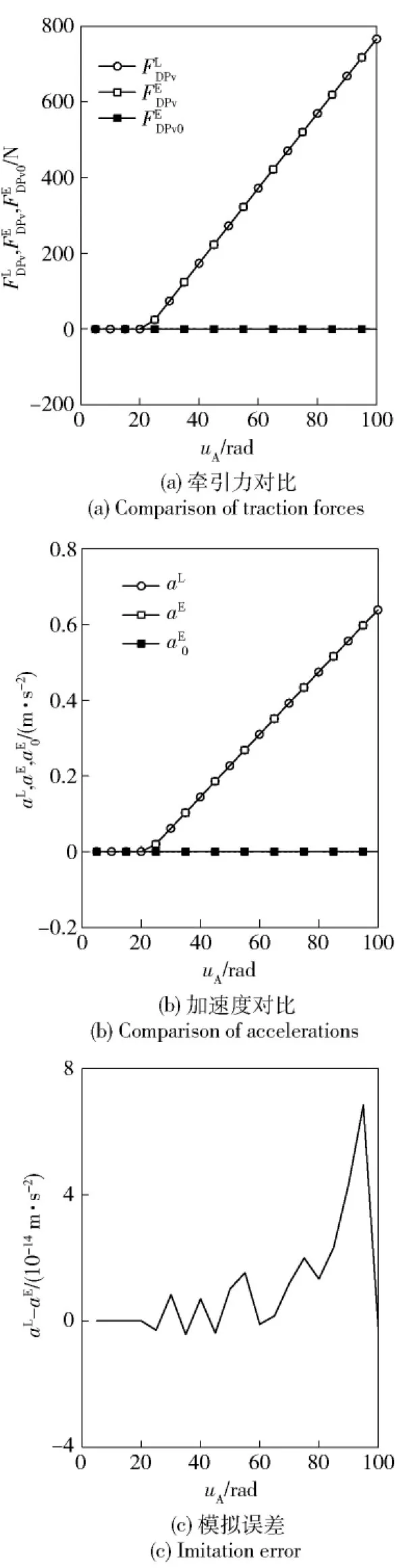
使用(34)式的整车牵引力计算公式和图2的直线加速度模拟驱动算法，可以得到相同垂直载荷下的月面载人月球车和地面模拟车的整车牵引力、整车加速度和加速度模拟误差，如图6所示。

由图6(a)可见，相同垂直载荷的地面模拟车非模拟状态与月面载人月球车在使用相同车轮驱动力矩时，能够产生完全相同的整车牵引力，模拟算法驱动的地面模拟车整车牵引力为月面载人月球车整车牵引力的1/6. 结合图6(b)和图6(c)可知：不采用加速模拟算法驱动的地面模拟车虽然能够产生相同的整车牵引力，但是由于月面载人月球车和地面模拟车质量不同，地面模拟车整车直线加速度为月面载人月球车整车直线加速度的6倍；而采用模拟算法驱动的地面模拟车，始终能够保持与月面载人月球车相同的整车直线加速度，并且模拟误差不超过2×10-14m/s2，始终保持较高的模拟精度。

4 地面模拟实验

采用如图7所示地面模拟车对月面载人月球车进行直线加速模拟。

地面模拟车包括整车控制器与移动系统，整车质量为200 kg，可用于模拟相同垂直载荷条件下表2中质量1 200 kg月面载人月球车的直线加速行驶实验。整车前轮和后轮轴距为2.5 m，质心距离前轮1.293 m，质心距离后轮1.207 m，车轮宽0.23 m，车轮半径0.4 m. 另外，地面模拟车车轮采用特殊筛网形式车轮，其r、b、n、j、c的修正系数参数λr、λb、λn、λj、λc如表3所示[5]。

表3 车轮修正系数

由于无法直接获取月面载人月球车的实际加速情况，因此分别对月面载人月球车车轮扭矩为130 N·m、140 N·m、150 N·m时的整车直线加速度进行理论计算，计算结果如表4所示。采用图2的模拟算法，可以获得相应地面模拟车直线加速模拟时所需的车轮扭矩。实验中，使地面模拟车车轮达到表4中的稳定扭矩，测量5～10 s之间的车速，并通过计算获得相应平均加速度，实验结果如表4所示。

表4 模拟实验结果

由表4实验数据可以看出：地面模拟车不采用模拟算法时，其平均加速度最大误差超过0.700 m/s2；采用模拟算法其直线加速度最大误差不超过 0.019 m/s2，具有较高模拟精度。

5 结论

通过建立月面载人月球车直线加速的整车力学模型，本文分析了由于地面重力和月面重力不同导致的地面模拟车难以产生与月面载人月球车相同直线加速度的原因，推导了车辆力矩驱动方式的地面模拟车整车直线加速模拟算法。通过计算和分析获得了如下结论：

1)当月面载人月球车和地面模拟车具有相同整车质量，并使用完全相同的驱动力矩时，由于地面模拟车整车垂直载荷是月面载人月球车整车垂直载荷的6倍，无法克服过大压土阻力，从而无法产生整车牵引力和整车直线加速度。如果使用加速模拟算法驱动地面模拟车，其可产生与月面载人月球车相同的整车直线牵引力，并获得高精度的整车直线加速模拟。

2)当月面载人月球车和地面模拟车具有相同垂直载荷时，若二者使用完全相同的驱动力矩，地面模拟车可以获得与月面载人月球车相同的整车牵引力，但由于地面模拟车整车质量是月面载人月球车整车质量的1/6，获得的地面模拟车直线加速度是月面载人月球车直线加速度的6倍。如果使用加速模拟算法驱动地面模拟车，产生的地面模拟车整车牵引力是月面载人月球车整车牵引力的1/6，并获得与月面载人月球车相同的整车直线加速度，达到高精度的直线加速度模拟。

本文仅考虑了整车直线加速的模拟，并未考虑月面载人月球车转向运动过程中的侧向力作用。因此，在地面模拟车对月面载人月球车的转向运动模拟时，需要考虑侧向力与切向牵引力的耦合作用，这也对全面实现模拟月面载人月球车的行驶提出了更多新的挑战。