双块零扩展截断相关的长码信号快速捕获算法

冯永新， 任锦君， 刘芳

(1.沈阳理工大学 研究生学院， 辽宁 沈阳 110159； 2.沈阳理工大学 信息科学与工程学院， 辽宁 沈阳 110159)

0 引言

扩频通信是一种保密性能好、截获概率低、抗干扰能力强的通信技术，广泛应用于军事通信系统中。伪扩频码的同步捕获[1-4]是扩频通信的关键技术，随着军事通信信号所使用的序列周期逐步增长，长周期伪码的快速捕获己成为亟待解决的关键问题之一。

对于高速率、长周期的伪码，直接捕获难度较大，需要较长的捕获时间和巨大的运算量。长周期PN码的捕获过程[5-8]是一个二维搜索过程[9]，即在频率域和时间域中去除载波频偏模糊和码相位模糊。对于直扩序列而言，多采用快速傅里叶变换(FFT)来实现伪码的二维捕获，但对于超长周期伪码来说，仅利用FFT相关处理很难实现伪码的快速捕获。近年来国内外对伪码的直接捕获技术[10-11]进行了大量研究，取得了不少的进展。目前，长周期伪码快速捕获算法[12-13]主要分为时域快速捕获算法与频域快速捕获算法。在时域快速捕获算法中，常对本地长周期序列进行时域处理，从而提高捕获速度。文献[14-15]中讨论了扩展复制重叠(XFAST)算法，在伪码的优良相关性基础上，利用折叠码段，扩展了一次捕获搜索范围，以提高捕获速度，但存在多普勒频移条件下其使用有最低载噪比的限制问题。文献[16-17]引入了以循环相关为基础的均值快速捕获算法，不仅采用了循环相关的方法使搜索时间覆盖域扩大，以提高捕获速度，而且通过分段捕获很好地实现了伪码多普勒频移补偿。文献[18]则研究了结合均值算法与扩展重叠算法的改进PN码直捕方法，提高了捕获效率，但会导致相关峰信噪比(SNR)损失较大，不适合信噪较低的环境条件。此外，部分算法用小波变换[19]代替FFT进行时域到频域计算，可降低数据量，并对多普勒频率进行估算。以上几种时域处理方法均可降低运算开销[20]，提高捕获速度，但同时引入了背景噪声，捕获环境受限，捕获性能随捕获速度的提高而有所下降。

针对上述问题，双块零扩展(DBZP)[21-25]技术立足于快速捕获的角度, 可解决传统方法实现捕获时出现的准确性及快速性问题，但对于长周期伪码等数据处理量大的信号，其算法运算开销稍高，仍存在捕获速度的局限性。为此，利用DBZP算法中双块零扩展与圆周移位技术，结合截断相关、能量补偿技术进行优化改进，提出了一种DBZP截断相关(TC-DBZP) 的长码信号快速捕获算法。该算法不但实现了长周期伪码的快速捕获，且能很好地适应捕获环境。

1 TC-DBZP快速捕获算法

不失一般性，以直接序列扩频信号(DSSS)作为射频接收信号，经降频及采样处理后，信号可表示为

SIF(tn)=
P(tn)D(tn)cos[2π(fIF+fd)tn+θ0]+N(tn)，

(1)

式中：tn为第n采样点对应的采样时刻；P(tn)为tn时刻非周期或长周期性调制扩频PN码；D(tn)为tn时刻调制数据；fIF为中频频率；fd为多普勒频移；θ0为载波初始相位；N(tn)为tn时刻引入的噪声。

接收信号SIF(tn)分别通过两路相互正交的通道进行处理，复合形成复接收信号序列，其表达式为

Sp(tn)=Ap(tn)exp[j2πΔfdtn+θe]+n(tn)，

(2)

式中：Ap(tn)为信号SIF(tn)经正交通道处理后的扩频PN码及数据；Δfd为处理后的多普勒频移，且Δfd=fd-d，d为本地载波同步后多普勒频移量；θe为处理后的相位；n(tn)为处理后的噪声。

利用复序列频谱的非对称性，分别在频域对复信号序列Sp(tn)和本地生成PN码序列Ploc(tn)进行截断预处理。首先，接收机从第j个采样点对应的tj时刻对序列Sp(tn)截取长度为N(n=1,2,…,N)的数据并进行FFT频域变换，其表达式为

(3)

式中：FFT(·)为FFT变换。同时，对本地伪码生成器产生的PN码序列Ploc(tn)，截取长度为N的数据，做FFT频域变换，其表达式为

(4)

由于复接收信号序列Sp(tn)的有效信息集中分布在其谱线前半部分，后半部分所含信息量较少。根据其非对称性，截取Ω(n)前半部分频点序列，形成新的复接收信号频域序列Ωh(n)。同理，截取P(n)的前半部分频点序列，形成新的本地扩频伪码信号频域序列Ph(n)。

将截断后的序列Ωh(n)与序列Ph(n)进行逆傅里叶变换，其表达式分别为

(5)

(6)

式中：[·]T为对信号序列进行转置；IFFT(·)为对信号序列进行逆傅里叶变换。

进一步，引入双块零扩展和圆周移位的思想进行分块相关处理，使相同捕获精度下捕获速度得到进一步提高，TC-DBZP算法捕获过程如图1所示。

图1 TC-DBZP算法捕获过程Fig.1 Flow chart of TC-DBZP acquisition algorithm

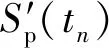
(7)

式中：fs为接收机采样频率；Nb为数据分块数。此外，通过分块扩展过程的参数设定来控制同步精度，进而解决同步效率问题。按设定的分块大小Sb对相关数据进行分块处理，αi、βi分别为经分块处理后的复接收信号序列与本地伪码信号序列：

(8)

(9)

对(8)式、(9)式所得信号序列分别进行双块扩展与补零扩展，其扩展过程可表示为

(10)

(11)

(12)

经长数据分块相关后，得到Nb个相关结果ξi(τ,Δfd)，形成大小为Nb×2Sb的相关结果矩阵ξ(τ,Δfd)，如(13)式所示，并对ξ(τ,Δfd)进行处理分析。将ξ(τ,Δfd)分成两个大小为Nb×Sb的相关子结果εNb×Sb和ζNb×Sb，且相关结果的有用数据集中在子结果εNb×Sb中，则εNb×Sb为该轮捕获结果。

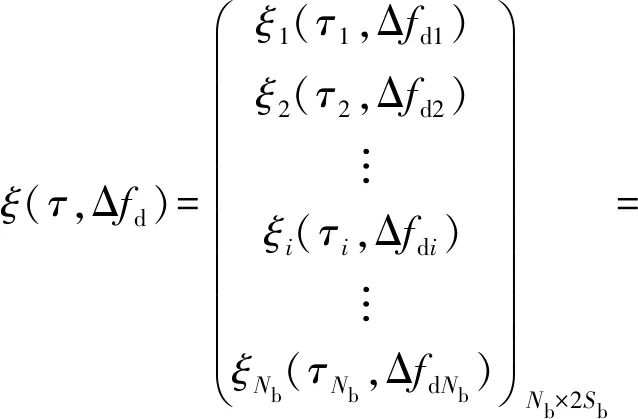
(13)

在分块相关过程中，对块中数据进行相关运算，当伪码偏移量大小达到块内伪码搜索范围的边沿时，块内接收信号序列与本地伪码序列的相关度较低，捕获峰值能量低于判决门限，易发生漏捕现象，使成功捕获概率下降，若将其捕获结果舍弃，亦降低了运算结果的利用效果。因此，对捕获结果进行能量补偿处理，增加相关结果的峰值能量，提高成功捕获概率。

(14)

进一步，将其前半部分进行补零处理，补零形结果χNb×Sb，可表示为

(15)

随后，本地伪码序列圆周移动一个子块长度进入下一轮捕获。若在下一轮捕获中伪码偏移量没有在该块的块内伪码搜索范围内，则捕获失败。由此，按照以上处理方法对相关捕获结果的后半段结果保留，经补零生成补偿结果，再次将本地伪码序列圆周移动一个子块长度进入下下轮的捕获，以此类推，当完成整个伪码偏移范围的搜索时，产生N个补偿结果。作为下一次对整个伪码偏移范围的搜索能量补偿，可表示为

χ=[χNb×Sb,1,χNb×Sb,2,…,χNb×Sb,i,…,χNb×Sb,N].

(16)

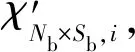
KNb×Sb,i=εNb×Sb,i+χNb×Sb,i.

(17)

经补偿处理后分块相关所得结果KNb×Sb,i的结果峰值，作为本轮分块相关的结果峰值，进入捕获门限判决阶段，完成伪码的捕获，对列做谱分析可得到载波多普勒频率的相关结果，从而实现了对伪码偏移与频率多普勒的捕获。若捕获成功，进入跟踪阶段，否则对整个伪码偏移范围进行重新捕获。在算法中，将双块零扩展与伪码圆周移位相结合，减少了非相干累积次数，并将原来的频率、相位的二维搜索过程转化为一维捕获，可大大减少搜索时间，从而提高(改善)了捕获速度，并对后续算法性能的优良予以方针指导和分析。

2 算法性能仿真与分析

为了验证本文算法的有效性与先进性，对捕获时间这一重要指标进行对比分析。在信号同步捕获的长期研究中，最常见且有效的信号伪码偏移及多谱勒频偏同步方法为二维搜索捕获方法[26]，不同捕获算法结合二维搜索对信号进行同步，其中影响其捕获时间的主要因素为伪码偏移范围、频偏搜索范围以及搜索精度。为方便分析，设所分析指标捕获时间设为T，影响伪码偏移范围和频偏搜索范围因素分别为Df和Dw，且与分析指标呈正比关系；频率偏移单元搜索精度和伪码偏移搜索精度分别为Sf和Sw，且与分析指标呈反比关系。因此，常见的二维搜索捕获方法的捕获时间可表示为

(18)

考虑到捕获时间T又与算法本身特点和复杂程度有关，用系数表示此类影响，记为A.

本文所提出的算法将DBZP算法与截断相关相结合，由于DBZP算法的结构特殊性，将原来的频率、相位的二维搜索过程转化为一维捕获，故其捕获时间表示为

(19)

此外，算法结合了截断相关算法，即相关过程时间减半，故其捕获时间最终表示为

(20)

鉴于算法捕获效率与算法复杂程度有关，由自身特点决定，故研究各算法的捕获时间分布这一重要分析指标还需进行仿真实验，因此需要基于MATLAB仿真环境进行仿真与分析。为保证算法适用的普遍性，仿真选定在多组不同的伪码速率和码周期条件下进行。同时为满足实验效率，均截取相同码片长度的信号进行对比分析。其余参数环境设置为：截取信号码片长度为6 000码片，载波频率fm为40.96 MHz，采样频率fs为163.84 MHz，信噪比SNR为-20～5 dB，多普勒频移搜捕范围设定为0～10 kHz. 为评估二维捕获环境下的捕获性能，采用仿真数据集对捕获算法进行测评，并在不同影响因素下，同普遍使用的时域快速捕获算法如均值捕获算法、XFAST捕获算法以及未经截断预处理和能量补偿的DBZP算法进行比较分析。此外，本文算法的有效性还可从环境适应性角度进行对比分析，接下来将从这两种角度展开对算法的性能分析。

2.1 捕获速度分析

影响二维捕获速度的主要因素有：多普勒频移、频率搜索步进量与伪码偏移量，考虑到这些因素对3种算法的影响不尽相同，故针对不同因素做以下仿真与分析。

2.1.1 基于多普勒频移的分析

由于频率多普勒与频率搜索步进量在频域搜捕中相互牵制影响，需同时分析其对二维捕获速度的影响程度。综合考虑仿真拟合实际接收信号的捕获过程，设定在伪码搜索范围为6 000码片，频偏搜索范围0～10 kHz，频率搜索精度200 Hz下进行仿真分析。同时，为对不同伪码偏移条件进行全面分析，选取码偏在伪码搜索范围的30%、60%、80%附近进行大量仿真，图2为在设定搜索范围内选取码偏约在30%、60%、80%位置处时，其捕获时间分布情况。

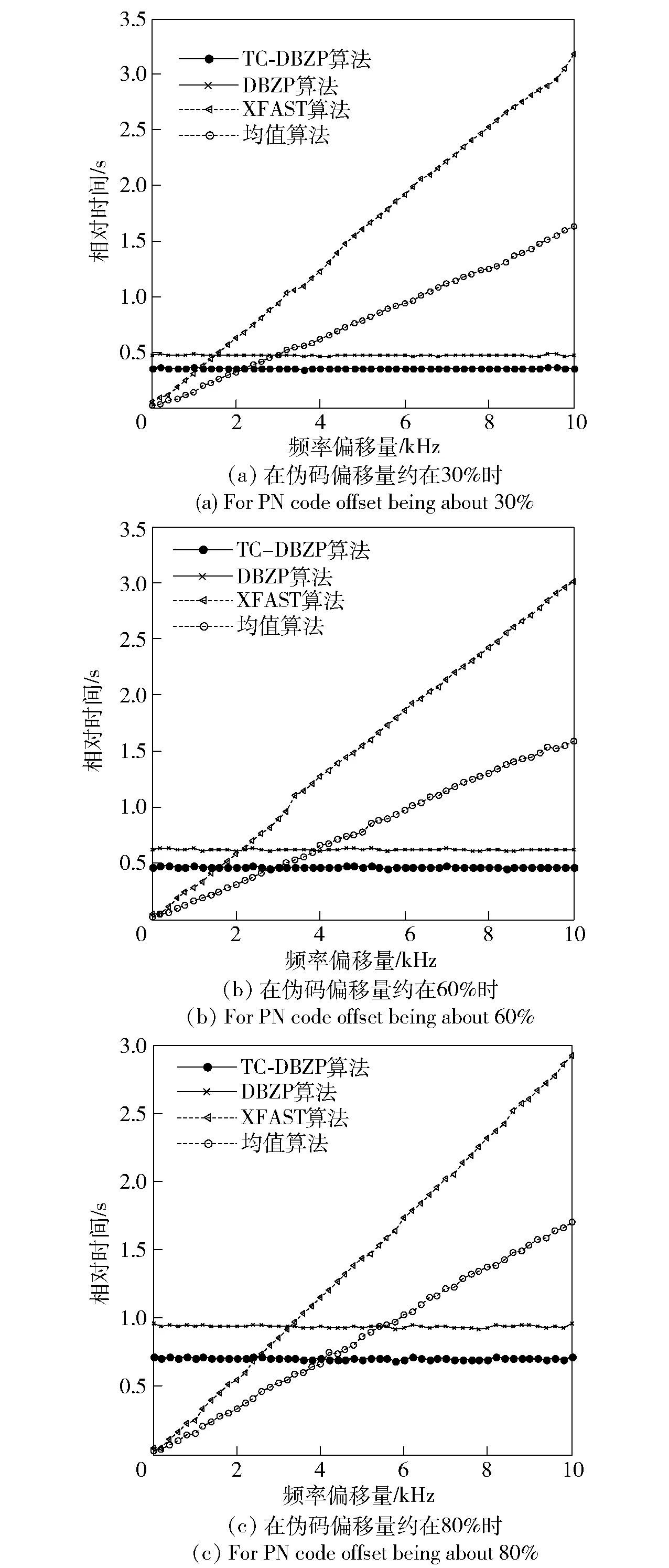
图2 不同伪码偏移量条件下受多普勒频移影响的算法捕获时间分布图Fig.2 Distribution graphs of acquisition times of algorithms affected by Doppler frequency shift in the case of different PN code offsets

由图2可知，采用二维捕获方法的均值算法与XFAST算法的捕获速度，主要受多普勒频偏影响，随频偏增加，其捕获时间随之增长。相反，由于DBZP方法对多普勒频偏捕获的独特性，TC-DBZP算法与DBZP算法的捕获速度，受同步前分块扩展的设置参数所决定，并不随所需捕获的频偏值的改变而改变，且由图2对比分析可得，其主要受伪码偏移量影响，搜捕时间随伪码偏移量增大而增长，但捕获速度仍优于前两种算法，且TC-DBZP算法运用截断相关技术，相比于DBZP算法，捕获速度提高了约25%. 因此，分析表明本文算法适合在小伪码偏移条件下进行高效快捕，在该环境下更能凸显其速度优势，在其他环境下虽存在速度优势，但受参数影响优势不够明显。

2.1.2 基于频率搜索步进量的分析

频率多普勒搜捕过程中，频率搜索步进量影响其搜捕速度，频率搜索步长增大，其搜索速度随之加快。由2.1.1节分析可知，时域快速捕获受伪码偏移量影响较小，又考虑到频率多普勒搜捕的精度受限，因此选取伪码偏移量在伪码搜索范围的60%附近，在不同频率搜索步进量条件下进行仿真分析，随搜捕频率的增加，其捕获时间分布结果如图3所示。

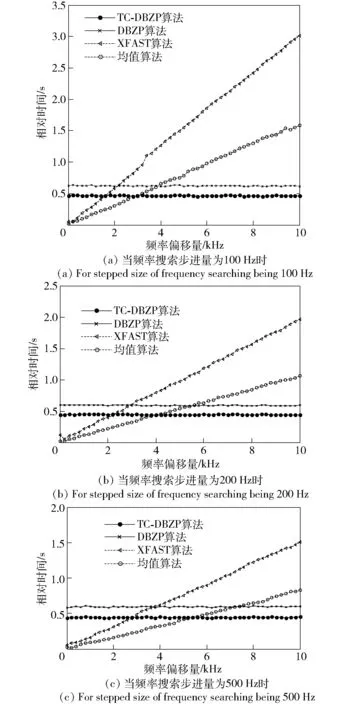
图3 不同频率搜索步进量条件下受多普勒频移影响的算法捕获时间分布图Fig.3 Distribution graphs of acquisition times of algorithms affected by Doppler frequency shift in the case of different stepped sizes of frequency searching

由图3(a)～图3(c)对比可知，在相同伪码偏移与多普勒频移下，均值算法捕获速度与XFAST算法捕获速度受频率搜索精度影响，随频率搜索步长增大，搜索速度明显加快，所用时间显著缩短。然而，这将导致频率搜索精度降低，频率多普勒搜捕的准确率相对受损。而TC-DBZP算法捕获速度，虽受频率搜索精度的影响，主要由同步前分块扩展的设置参数所决定，即在二维捕获中捕获速度相对稳定，且在均值算法捕获速度、XFAST算法捕获速度提高的情况下，仍优于这两种算法，且在高频率搜索精度下优势明显，在低频率搜索精度下优势不够明显，因此该算法更适合高精条件下的同步。

2.1.3 基于伪码偏移量的分析

由于TC-DBZP算法主要受伪码多普勒影响，在伪码搜索范围与频偏搜索范围条件一定、频率搜索精度相同(200 Hz)情况下，分析伪码偏移量对捕获速度的影响程度。为对不同多普勒频偏进行全面分析，选取频偏搜索范围在30%、50%、80%附近进行大量仿真，其中频偏约为30%、50%、80%位置处捕获时间分布情况如图4所示。

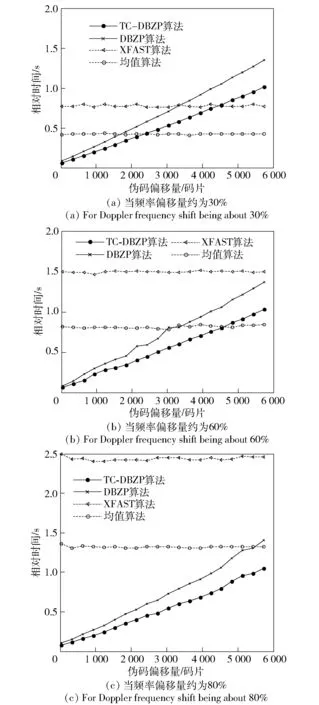
图4 不同频率偏移量条件下受伪码偏移影响的 算法捕获时间分布图Fig.4 Distribution graphs of acquisition times of algorithms affected by PN code offset in different Doppler frequency shifts

由图4(a)～图4(c)明显看出，TC-DBZP算法捕获速度主要受搜索的伪码偏移影响，随搜捕码偏增大，搜索时间增加。该算法捕获时间无论在频偏较小或频偏较大时，其捕获速度相对于XFAST算法捕获速度均占优势。相比于均值算法，在频偏较小时，其速度并不占明显优势；但当频率偏移量增大时，速度优势突出。

综上所述，本文算法在捕获频率搜索精度要求相对较高时，在小伪码偏移、大频率偏移的捕获情况下，其捕获速度明显高于其他3种捕获算法。在其他捕获情况下，虽然算法本身特点存在速度优势但是优势不明显。

2.2 环境适应性分析

为了提高算法的环境适应性，TC-DBZP算法采用能量补偿处理，以减少漏捕现象发生，提高捕获成功概率。为了验证合理性，将能量补偿前与引入后的TC-DBZP算法分别对中频采样频率为40.96 MHz、多普勒频移为1.15 KHz、伪码偏移为2 435码片的直接序列扩频信号在信噪比范围为-20～5 dB环境下进行捕获，设捕获判决门限为5，捕获相关结果如图5、图6所示。

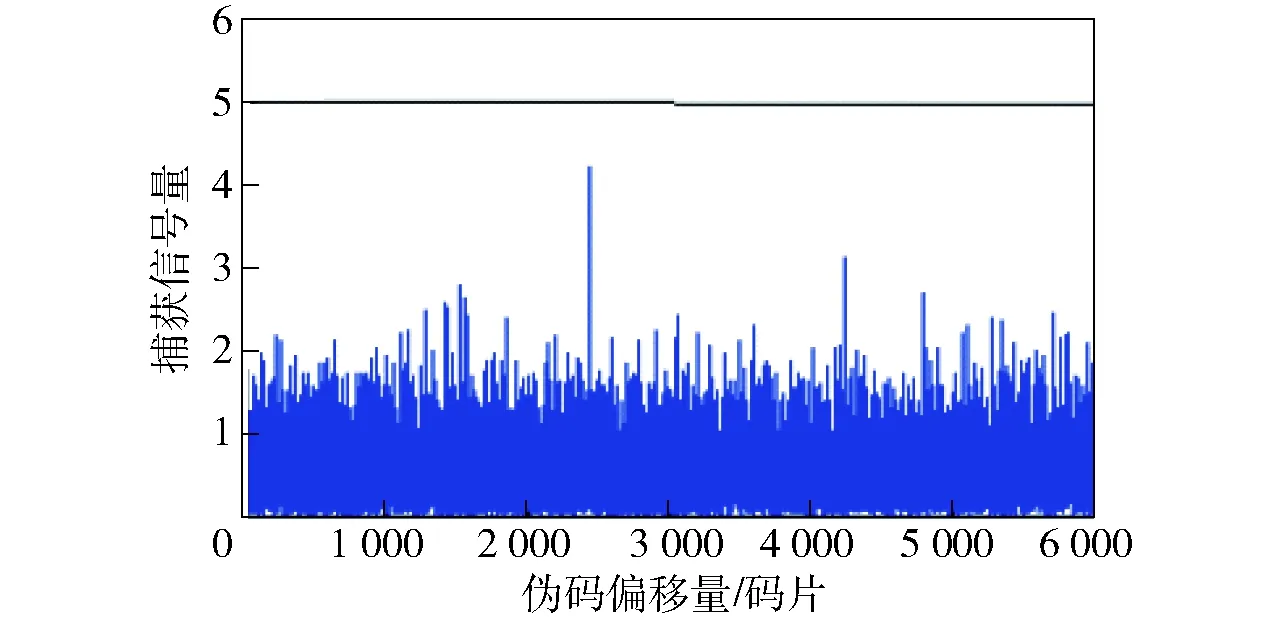
图5 未引入能量补偿的TC-DBZP算法捕获结果图Fig.5 Acquisition result of TC-DBZP algorithm without energy compensation

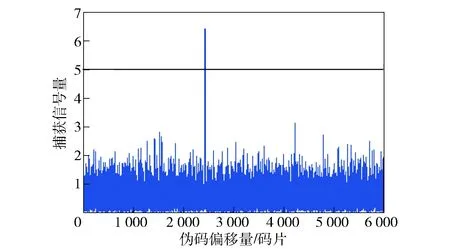
图6 引入能量补偿的TC-DBZP算法捕获结果图Fig.6 Acquisition result of TC-DBZP algorithm with energy compensation

本轮仿真验证所选取的伪码偏移量位于分块相关过程中块内伪码搜索范围的边沿，由图5、图6对比看出，引入能量补偿的TC-DBZP算法捕获效果明显，块内伪码搜索范围的捕获峰值能量提高，可减少因块内信号序列与本地伪码的相关重合度低导致的峰值能量受损，捕获峰值低于判决门限引发的漏捕现象，且受噪声干扰影响降低，从而提高了成功捕获概率。

为了进一步考察TC-DBZP算法在不同环境下的捕获适应性，对DSSS信号数据进行实验。仿真参数设置为：中频采样频率为40.96 MHz，搜索步长为300 Hz，多普勒频移搜索范围为-10～10 MHz，伪码偏移范围为0～6 000码片，信噪比范围为-20～5 dB. 在上述仿真条件下，对4种捕获算法进行100次蒙特卡洛实验，算法捕获峰值对比图如图7所示。

图7 不同信噪比下算法捕获峰值对比图Fig.7 Comparison graph of algorithms’ acquisition peaks at different SNRs

由图7可知，算法捕获能效受噪声干扰影响，随噪声增大，信噪比降低，捕获峰值随之降低。传统XFAST算法、均值算法的捕获峰值随信噪比减小而大幅度降低；TC-DBZP算法与DBZP算法随信噪比减小而小幅度降低。并且，相比DBZP算法，经能量补偿处理的TC-DBZP算法捕获效率得到部分提高。在信噪比小于-5 dB/Hz的条件时，本算法比均值算法的捕获峰值高约30%，比XFAST算法的捕获峰值高约40%. 因此，相比于其他3种算法，新算法的环境适应性较好。

由2.1节研究可知，本文算法在频率搜索精度相对较高时，在小伪码偏移、大频率偏移情况下捕获速度明显优于其他3种算法，因此针对小伪码偏移、大频率偏移的特殊情况进行环境适应性的仿真。为此在伪码偏移为0～2 000码片，多普勒频移为6～10 kHz条件下对4种捕获算法进行100次蒙特卡洛实验，算法捕获峰值对比图如图8所示。

图8 在小伪码偏移量和大频率偏移情况下不同信噪比时算法捕获峰值对比图Fig.8 Acquisition peaks of algorithms at different SNRs in the case of small PN code offset and large Doppler frequency shift

由图8可知，在小伪码偏移量、大频率偏移的特殊条件下，虽算法捕获峰值有所降低，相比其他算法，其环境适应性仍保持稳定。由此表明，TC-DBZP算法，相比均值算法、XFAST算法，其捕获性能相对稳定，受噪声干扰影响相对较小，环境适应性较高。

3 结论

本文提出了一种TC-DBZP的长码信号快速捕获算法，并从捕获速度和环境适应性两种角度展开对算法捕获效率的分析。仿真结果表明，TC-DBZP算法在捕获的多普勒精度相对较高时，在捕获速度方面优于常用的3种时域捕获算法，特别是在小伪码偏移、大频率偏移条件下优势较为明显，并且受噪声干扰影响相对较小，捕获性能相对稳定，环境适应性好。