基于Jones-Wilkins-Lee状态方程的爆轰波相互作用参数理论分析
2019-04-17李瑞李伟兵靳洪忠王桂林洪晓文朱建军李文彬王晓鸣
李瑞, 李伟兵, 靳洪忠, 王桂林, 洪晓文, 朱建军, 李文彬, 王晓鸣
(1.南京理工大学 智能弹药技术国防重点学科实验室, 江苏 南京 210094; 2.山东特种工业集团有限公司, 山东 淄博 255201; 2.重庆红宇精密工业有限责任公司, 重庆 402760)
0 引言
提高战斗部主装药的炸药能量利用率是战斗部设计者追求的一个重要目标。在实际中,一般通过采用隔板、多点起爆或复合装药等方式调整爆轰波波形,使爆轰波在对称面处发生汇聚,形成超压爆轰,这些方式在高速杆式射流、大长径比爆炸成型弹丸以及定向战斗部等方面应用非常广泛[1-4]。
在20世纪70年代,Al′tshuler等[5]通过试验发现了B炸药的超压爆轰现象,测得了超压爆轰的爆速是正常爆轰的2倍,爆压超过120 GPa. Dunne[6]、缪玉松等[7]基于等γ律状态方程对凝聚炸药爆轰波碰撞过程进行了理论分析,并指出发生马赫反射的临界入射角取决于爆轰产物的多方指数γ,给出了马赫反射压力等参数的计算方法。Zhang等[8]基于质量守恒定律给出了爆轰波传播过程中马赫杆高度的计算模型。潘建等[9]利用Whitham方法[10-11]分析了爆轰波相互作用过程,并计算了爆轰波的马赫反射参数。Lambourn等[12]利用Whitham方法计算了凝聚炸药爆轰波碰撞的马赫反射问题,计算过程中对面积函数进行了修改,修改后的计算结果和试验结果符合得很好,但修改后的面积函数中慢变函数需要根据试验数据拟合确定,给马赫反射参数的理论计算带来不便。
本文基于Jones-Wilkins-Lee(JWL)状态方程,利用三波理论[6]和Whitham方法[10-11],对爆轰波相互作用后的正规斜反射和马赫反射进行理论分析,确定Lambourn等[12]修改后的面积函数中慢变函数理论计算方法,并进行验证,为进一步完善凝聚炸药爆轰波相互作用后的正规斜反射和马赫反射理论计算提供借鉴。
1 爆轰波碰撞计算模型
1.1 爆轰波相互作用
两个等强度爆轰波在炸药内部传播至对称平面处时,随着波阵面间夹角的增加将发生正碰撞、正规斜碰撞和马赫碰撞等过程。两个等强度爆轰波的正规斜碰撞和马赫碰撞,可视为其中一侧爆轰波对刚性壁面的正规斜反射和马赫反射,当入射角θ0较小时,将发生正规斜反射,如图1(a)所示,此时流出波阵面TI和流出波阵面TR的流团偏转角相等,即φ1=φ2. 随着入射角θ0的不断增大,达到马赫反射的临界入射角θ0c以后,碰撞点附近物质发生堆积,迫使碰撞点T移动至T′点,便形成了如图1(b)所示的马赫反射。图1中:0区为原始炸药区,1区为入射爆轰波后区,2区为反射波后区,3区为马赫杆后区;q0、q1、q2、q3分别为入射波TI、反射波TR及马赫杆TT′前后的流团速度;DCJ和uCJ分别为入射波TI的波速和波后介质的移动速度。
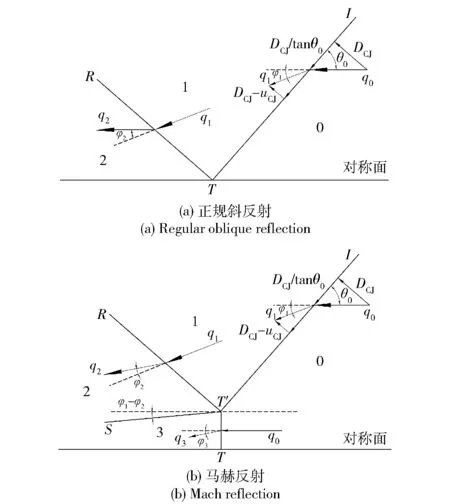
图1 爆轰波正规斜反射和马赫反射流场Fig.1 Flow setup to describe regular reflection and Mach reflection
炸药JWL状态方程及其等熵形式[13]为
(1)
(2)
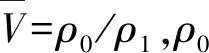
对于爆轰波正规斜碰撞,首先考察图1(a)中由0区到1区各参数间的变化关系。假设炸药完全反应,1区中爆轰产物满足C-J条件,根据入射波TI切向速度连续、质量守恒、动量守恒以及C-J条件得到1区流团速度为
(3)
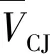
按照入射波TI前后的几何关系,结合三角函数关系式,得
(4)
对于1区到2区,根据压力- 转角关系式[14],有
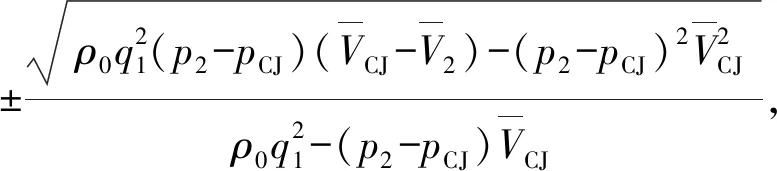
(5)
式中:p2为2区压力;pCJ为C-J条件下爆轰产物的压力。
对于爆轰波正规斜碰撞,首先根据入射角θ0及1区爆轰产物的C-J条件参数,由(3)式和(4)式计算出流团速度q1和入射波TI后流团偏转角φ1. 然后结合Hugoniot关系及JWL状态方程,由(5)式计算出反射波后流团偏转角φ2. 将(p2,φ1+φ2)的点作在图2上,得到反射波的极曲线R1,该曲线与p2轴交于a、b两点,根据附体激波都为弱激波解[14],显然a点即为正规斜反射的稳定解。当θ0增大到θ0c
时,a、b两点重合,与p2轴相切(曲线R2)。根据Von Neumann的脱体激波判据[14],θ0c即为正规斜反射向马赫反射转变的临界入射角。不同炸药的马赫反射临界入射角的理论计算值和试验结果如表1所示。从表1的计算结果中可以看出,基于JWL状态方程计算出的马赫反射临界入射角θ0c较等γ律状态方程的计算结果更接近于试验值。从而验证了基于JWL状态方程的马赫反射临界入射角计算的正确性。
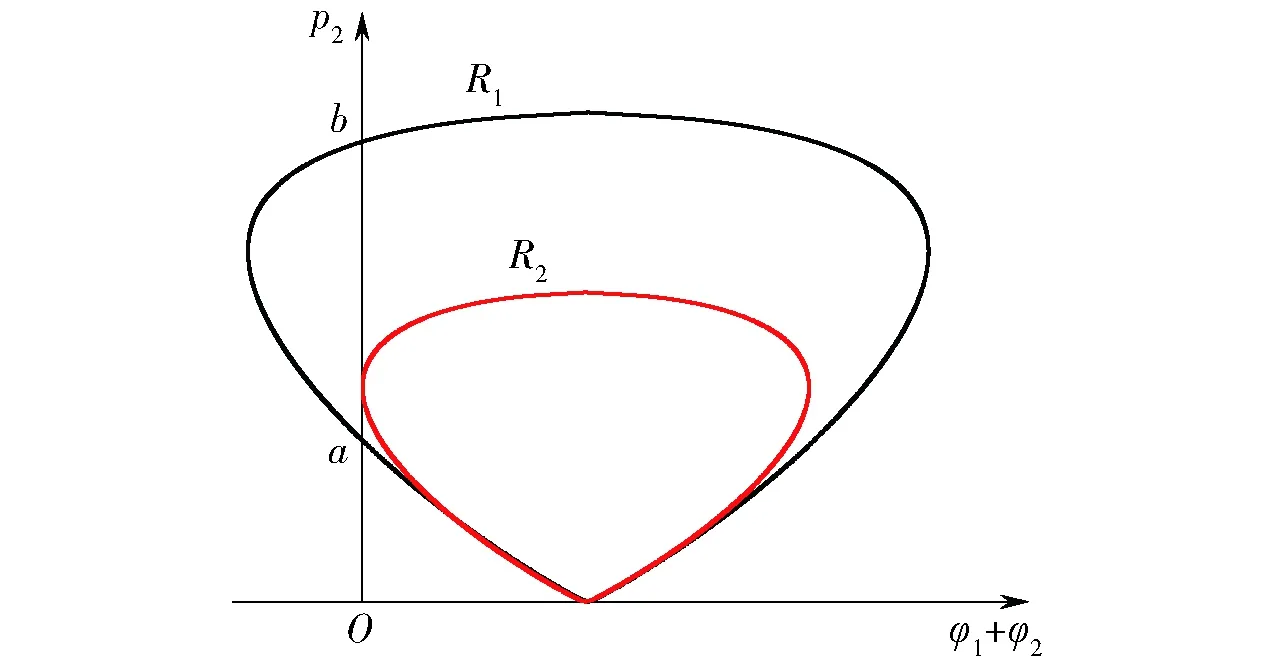
图2 不同入射角下的反射波压力- 转角极曲线Fig.2 Pressure-deflection curves at different incident angles
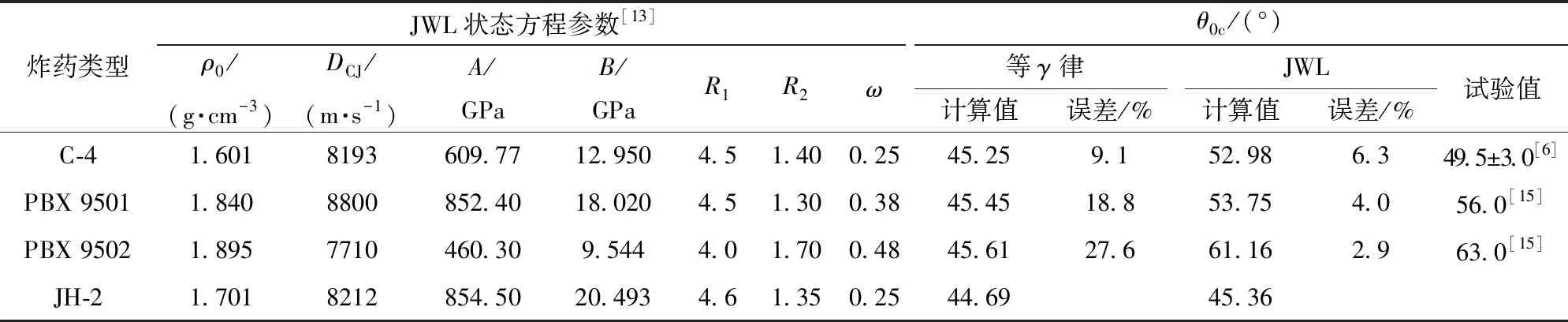
表1 不同炸药的马赫反射临界入射角计算值与试验结果
1.2 三波点增长角的确定
基于Whitham方法[10-11]获取三波点增长角,是基于把马赫杆看作入射爆轰波在一收敛的变截面流管中传播的结果,在二维情况下,爆轰波位置与其垂直的射线位置如图3所示。
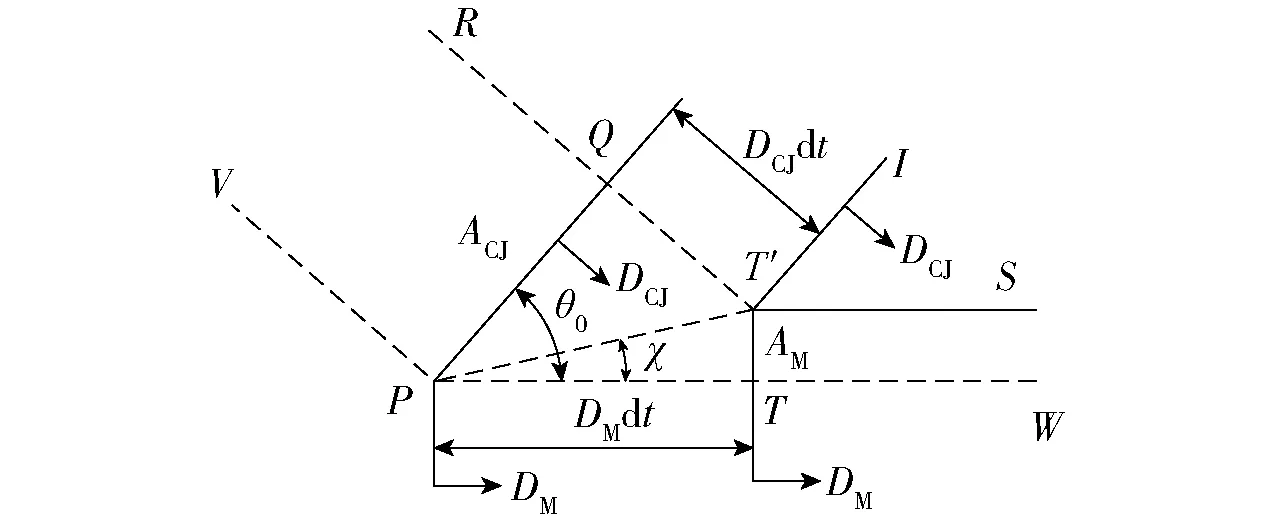
图3 Whitham方法描述爆轰波运动示意图Fig.3 Detonation wave movement described in Whitham’s geometrical shock dynamics
图3中VPTW和RQT′S两条线之间为一个变截面管道。PQ是t时刻入射爆轰波位置,TT′为t+dt时刻由入射爆轰波PQ变成的马赫杆。∠QPT为爆轰波入射角θ0,∠T′PT为三波点增长角χ.P、T′为不同时刻的三波点。由图3可得到:
cosχ/sin (θ0-χ)=DM/DCJ,
(6)
sinχ/cos (θ0-χ)=AM/ACJ,
(7)
式中:ACJ和AM分别为截面PQ和TT′处管道的面积;DM为马赫杆速度。
联立(6)式和(7)式,得
(8)
式中:马赫杆速度DM和入射爆轰波速度DCJ的关系定义[12]为
(9)
ξ=p3/pCJ,p3为马赫杆压力。
Lambourn等[12]通过数值计算拟合出如下的面积函数A(ξ)关系:
(10)
式中:k(ξ)是一个慢变函数,一般取常数,通常由试验数据拟合得到。
根据张俊秀等[16]的试验结果,通过(6)式~(10)式,得到马赫杆参数DM和χ的计算结果如表2所示。从表2中可以看出,通过Whitham方法计算获得的马赫杆速度DM和三波点增长角χ与试验结果吻合较好,说明此方法计算马赫杆参数是可行的。

表2 马赫参数的计算值与试验结果比较
1.3 马赫杆高度计算
凝聚炸药在端面发生环起爆以后,在炸药内部形成的轴对称爆轰波向装药中心轴线汇聚形成超压爆轰。随着入射角θ0的不断增大,达到马赫反射临界入射角θ0c以后,形成马赫反射,如图4所示。
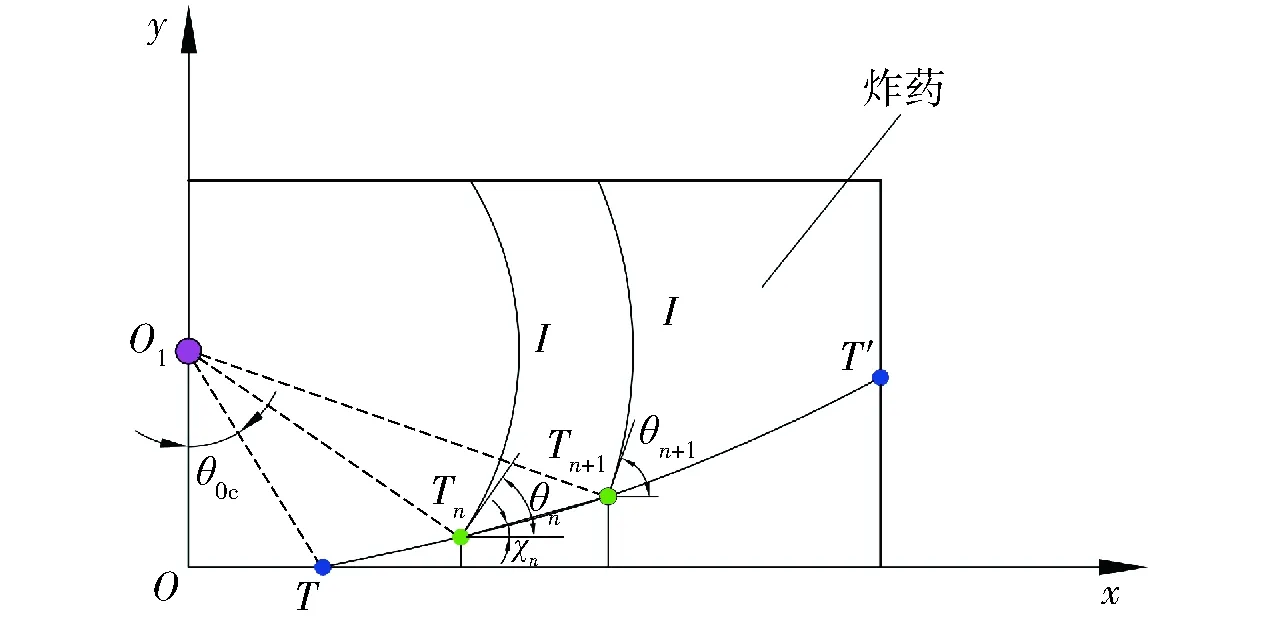
图4 爆轰波传播示意图Fig.4 Propagation of detonation wave
根据图4中的几何关系,马赫反射起始点T坐标(xT,yT)满足下面关系:
xT=rOO1tanθ0c,yT=0,
(11)
式中:rOO1为起爆半径。
令xn+1=xn+Δx,Δx为迭代步长,根据图4中的几何关系有
(12)
式中:θn和(xn,yn)分别为Tn点处的爆轰波入射角及Tn点坐标。
对于Tn点处的三波点增长角χn,根据图4中的几何关系有
(13)
式中:(xn+1,yn+1)为Tn+1点的坐标。Tn点坐标可由(8)式~(13)式迭代求出,依次连接Tn点坐标即可求出三波点轨迹,即马赫杆高度和传播距离的关系。
1.4 慢变函数k(ξ)的确定
虽然马赫反射参数可以用Lambourn等[12]修改的Whitham方法较精确地计算出,但对于不同炸药,慢变函数k(ξ)是不同的,需要根据试验数据拟合得到,这给马赫反射爆轰参数的理论计算带来不便,为此需对k(ξ)的理论计算进行推导。Whitham等[10-11]研究表明面积函数A(ξ)满足以下关系:
(14)
式中:D为爆轰波速度;u和c分别为爆轰波波阵面后介质的移动速度和当地声速;ρ为爆轰产物的密度。分别对(10)式和(14)式两边取自然对数,联立得
(15)
根据声速的定义[17],有
(16)
根据质量守恒和动量守恒定律,可计算得到爆轰波阵面后区压力p和介质的移动速度u为
(17)
将(17)式两边取微分,可得
(18)
根据JWL状态方程及Hugoniot关系,可计算爆轰波速度为
(19)
式中:E0为初始条件下炸药单位体积内能。
将(19)式两边取微分代入(18)式,对于给定ξ值(一般ξ取1~5),联立(15)式~(19)式即可计算出慢变函数k(ξ),其值变化较小,计算取平均值。
2 计算结果验证
2.1 压力计算与验证
为了验证本文计算模型的正确性,采用具有试验数据的PBX 9501炸药[17]进行验证。PBX 9501炸药的JWL状态方程参数见表1. 对正规斜碰撞的压力可由(1)式~(5)式,结合反射波(p,φ1+φ2)极曲线求得。对于马赫反射,首先根据(15)式~(19)式计算出慢变函数k(ξ),然后联立(8)式~(13)式计算出马赫反射压力,计算结果如图5所示。从图5中可以看出,计算出的正规斜碰撞和马赫碰撞的压力与试验结果较吻合,验证了基于JWL方程建立的正规斜反射和马赫反射压力以及慢变函数k(ξ)计算模型的正确性。
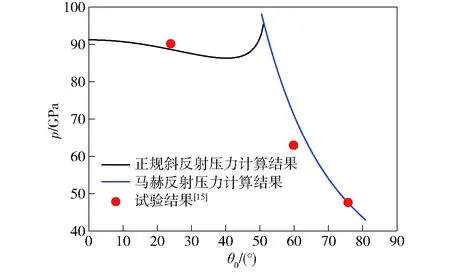
图5 PBX 9501炸药正规斜反射与马赫反射压力计算结果与试验结果对比Fig.5 Calculated and experimental results of regular and Mach reflection pressures of PBX 9501 explosive
2.2 马赫杆高度计算与验证
采用JH-2炸药[18]发生马赫反射后的马赫杆高度试验数据对本文马赫杆高度计算模型进行验证。JH-2炸药的JWL状态方程参数及马赫反射的临界入射角θ0c计算结果见表1. 根据(15) 式~(19)式计算出慢变函数k(ξ)=0.468 3,然后由(8) 式~(13)式迭代求出马赫杆高度,计算结果和试验结果对比如图6所示。从图6中可以看出,马赫杆高度计算结果与试验结果吻合较好,验证了马赫杆高度和慢变函数k(ξ)计算模型的正确性。
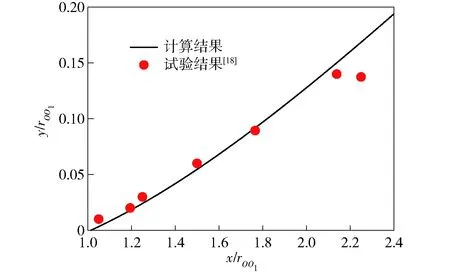
图6 马赫杆高度随传播距离变化的计算结果试验结果对比Fig.6 Calculated Mach stem heights and experimental data versus propagation distance
爆轰波正规斜反射和马赫反射的压力及马赫杆高度计算结果与试验结果吻合较好,说明基于JWL状态方程建立的正规斜碰撞和马赫碰撞的爆轰参数理论计算模型,能够较准确地反映实际凝聚炸药爆轰波正规斜反射和马赫反射的传播规律。
3 结论
1)本文基于JWL状态方程,建立了爆轰波正规斜碰撞压力计算模型和反射波的极曲线计算模型,计算得到了C-4炸药、PBX 9501炸药和PBX 9502炸药的马赫反射临界入射角θ0c,理论计算结果与试验结果的误差分别为6.3%、4.0%和2.9%,相比等γ律状态方程更接近于试验值。结合Whitham方法推导出慢变函数k(ξ)的计算公式,用PBX 9501炸药和JH-2炸药的试验结果验证了其正确性,这样可避免通过试验数据拟合慢变函数k(ξ),完善了马赫反射参数(马赫超压和马赫杆高度)的理论计算。
2)使用三波理论和Whitham方法,基于JWL状态方程建立的爆轰波斜反射和马赫反射压力及马赫杆高度计算模型,对于凝聚炸药爆轰波相互作用后发生的正规斜反射和马赫反射,能够较准确地反映其传播规律,为描述多点环起爆或带隔板装药条件下形成超压爆轰驱动药型罩过程提供理论基础。
