上市公司研发投入与财务业绩关系研究
2019-04-15杨瑞
杨瑞
近几年我国的科技创新能力发展迅速,但与发达国家相比还有较大的差距。我国为鼓励企业创新,在税收政策上提高了研究开发费用税前加计扣除比例,在利润表中新增“研发费用”项目,可见我国对于科技创新方面的发展非常重视。企业研发成功的产品会为企业创造价值,从而增强企业的财务业绩,然而研发投入也具有较大的不确定性,企业会面临研发失败的风险。因此,研发投入与企业业绩的关系一直备受国内外学者的关注。而所有权结构作为公司治理的基础,对于二者的关系也有一定程度的影响。因此,我们利用实证研究的方法,探求我国上市公司研发投入对其财务业绩的贡献以及所有权结构对二者关系的调节作用,希望可以为企业提供有效的建议。
一、文献综述
关于研发投入与企业财务业绩的研究,JS Lant和JM Sahut(2005)指出,如果企业能够立即从研发投入中获得商业利益,或者在未来获益时采取创新项目的集群战略,那么将研发投入资本化是比较可取的。FO Paula和JF Silva(2018)以欧洲制造企业为样本,研究发现研发投入不能影响整个样本的短期财务业绩。[在研发投入与所有权结构研究方面,Francis 和Smith(1995)研究时发现如果公司的股权结构更加集中,公司的研发投入将会增多。Katherine(2003)研究了企业研发投入与高管股权激励之间的关系,研究表明研发投入与高管持股比例呈正相关关系。关于所有权结构对研发投入与企业业绩的调节作用研究, Hall和Oriani(2006)对欧洲制造业企业的所有权集中度的调节作用进行研究,研究结果表明所有权集中度对研发投入与公司业绩之间的关系具有显著的正调节效应。
程宏伟、张永海、常勇(2006)的实证研究结果证实,公司在研发方面的投入与公司业绩显著正相关。 赵晖(2010)使用实证分析方法,对高新技术企业进行的研究表明,公司的研发投入与公司业绩正相关。刘雪瑶,张敏(2017)采用实证分析的方法对我国创业板上市公司的相关数据进行了分析研究,结果显示创业板上市公司的研发投入对企业财务业绩存在负相关效应。齐秀辉,王维,武志勇(2016)重点研究了高管激励机制对研发投入和企业业绩关系的调节作用。他们认为,公司所有权的形式对高管的激励有重要影响:在国有控股企业的背景下,高管激励对研发投入与企业业绩之间的关系具有显著的正调节效应;在对非国有控股公司进行比较研究时发现高管激励措施在对二者关系发挥了负面作用。
根据上述学者的研究结果,可以发现他们得出的结论不尽相同,这可能与他们所选择的样本企业、研究方法、研究变量不同有关,在大多数学者眼中,研发投入被认为与公司业绩正相关。目前,研究人员对所有权结构与研发投入,公司所有权结构和业绩之间的关系进行了深入研究,研究成果较为喜人,所有权结构在研发投入与企业业绩关系中发挥的调节作用也是近年来才引起了国内专家的关注。因此,本文对研发投入与企业业绩之间的关系进行研究并重点探讨所有权结构对研发投入与企业财务业绩的调节作用,从而为企业的所有权结构以及研发决策提供相关建议。
二、研究设计
(一)样本选择及数据来源
数据剔除了被ST特别处理的上市公司以及缺失相关数据的公司,从沪、深两市上市公司中找出了900家符合条件的上市公司。样本数据采用2014-2017年4年的数据。数据均来自Wind数据库,采用SPSS统计软件对数据进行处理。
(二)变量定义
表1 变量汇总表
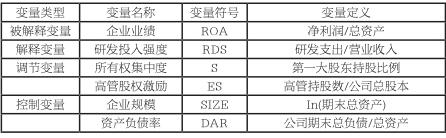
(三)模型的建立
为了研究研发投入对企业业绩的影响,构建了回归模型(1):
ROA=α+β1RDS+β2DAR+β3SIZE+ε
上述公式中ROA为样本公司的总资产报酬率,α为常数项,β为回归系数,RDS为研发支出占营业收入比例,DAR为资产负债率,该变量用于控制企业负债对财务业绩的影响,SIZE为总资产自然对数,该变量用于控制企业规模对财务业绩的影响,ε为随机变量。
研究所有权结构的变化对研发投入和公司业绩的影响,并建立回归模型(2):
ROA=α+β1 RD +β2OS *RDS+β3DAR+β4SIZE+ε
OS 代表所有权集中度(S)、高管持股激励(ES),其余变量解释与以上相同。
三、研究假设
本文结合上述学者的研究成果,提出以下研究假设:
H1:研发投入与公司业绩之间存在正相關的关系。有效的研发投入将构成公司的无形资产,从而会增加企业的核心竞争力,为企业带来收益,提升企业的财务业绩。
H2:所有权集中度对研发投入与企业业绩之间的关系具有正调节作用。 根据代理理论,所有权集中度越高的企业越有利于委托人对代理人的监督,提高其经营管理效率。
H3:高管股权激励对研发投入与公司业绩之间的关系具有正调节作用。根据代理理论,,代理人在公司中的持股份额越高,委托人与代理人的利益越紧密。为了实现共同的盈利目标,代理人将更加注重公司的技术创新活动。
四、实证研究
(一)相关性分析
为了尽可能避免回归模型的多重共线,在回归分析之前通过Pearson相关系数分析来分析变量之间的关系。如表2所示,ROA与RDS,RDS与S在1%的水平上显著负相关,其余变量之间在1%的水平上显著正相关。因此,如果模型中同时加入两个所有权结构变量,将会产生多重共线性问题。
表2 皮尔逊相关性分析

