新型空心板铰缝的受力性能
2019-04-15薛兴伟华旭东周俊龙
薛兴伟,华旭东,周俊龙
(沈阳建筑大学 交通工程学院,辽宁 沈阳 110168)
0 引 言
钢筋混凝土和预应力混凝土空心板梁桥因构造简单、施工方便、可大批量工厂化集中预制、装配式施工等诸多优势被广泛使用,成为小跨径桥梁(10~20 m)的首选桥型之一。
装配式空心板梁桥多以简支梁为主,其横桥向由多片预制的空心板组成,板间设置现浇的铰缝,在主梁架设完毕后,桥面浇筑9~15 cm厚的混凝土整体化层。通过桥面现浇层和铰缝,空心板梁桥各片空心板在横向实现剪力的传递,达到共同承担汽车荷载的目的。
然而,现有的装配式空心板梁桥经常出现铰缝的破坏。破坏程度轻的,企口缝混凝土与空心板侧壁相分离,雨水大量渗透并轻微侵蚀混凝土;破坏程度严重的,铰缝处混凝土已经完全脱落,受水的严重侵蚀,空心板失去横向连接能力和传力能力,出现“单板受力”现象[1-2]。
相关研究[3-9]表明:传统铰缝出现破坏的根本原因是,铰缝的宽度较小,铰缝下缘最窄处仅1 cm,企口处仅11 cm,导致整个铰缝的混凝土无法有效振捣,铰缝底部仅能填充水泥砂浆;传统铰缝内无法布置合适的受力钢筋,使得铰缝在纵桥向不具备抗弯和抗裂能力,在二期恒载、收缩徐变、温度梯度及汽车荷载的作用下,纵桥向将产生超过混凝土抗拉强度的拉应力,从而导致铰缝的开裂破坏。
传统的铰缝结构在设计上存在缺陷,在投入运营后必然出现开裂,进而失效,产生“单板受力”现象。因此,有必要设计一种可靠的铰缝结构,从根本上解决其先天不足的问题,以保证铰缝的正常工作和桥梁的整体受力[10-11]。
本文以交通部2014年标准图的13 m空心板桥为研究对象,设计了一种新型空心板铰缝结构,并通过建立Midasfea三维有限元分析模型,分析其主要的受力特征,并给出新型铰缝结构相应的配筋设计。
1 新型空心板铰缝
1.1 新型空心板铰缝结构
本文所提出的新型空心板铰缝结构如图1所示。图中铰缝的宽度为20~60 cm,相比传统铰缝有所增大,有利于铰缝混凝土的振捣,使得铰缝混凝土的施工质量得到有效保证;同时提供了布置纵向抗弯钢筋、横向抗弯钢筋的空间,使铰缝具备横向和纵向的抗弯能力。在预制空心板间设置横向搭接钢筋、箍筋,使得空心板与铰缝能更好地形成一个整体,具备更强的抗剪能力。
1.2 采用新型铰缝的空心板桥设计
选取交通部2014年标准图的13 m简支装配式先张法预应力空心板桥作为研究对象,如图2所示。其单幅桥宽12 m,荷载等级为公路I级。该桥由9片1 296 cm×124 cm×70 cm的预制空心板组成,边板挑臂为38 cm,空心板间铰缝底部宽1 cm,企口位置宽11 cm,桥面现浇层厚10 cm。空心板、铰缝及桥面现浇层均采用C50混凝土。
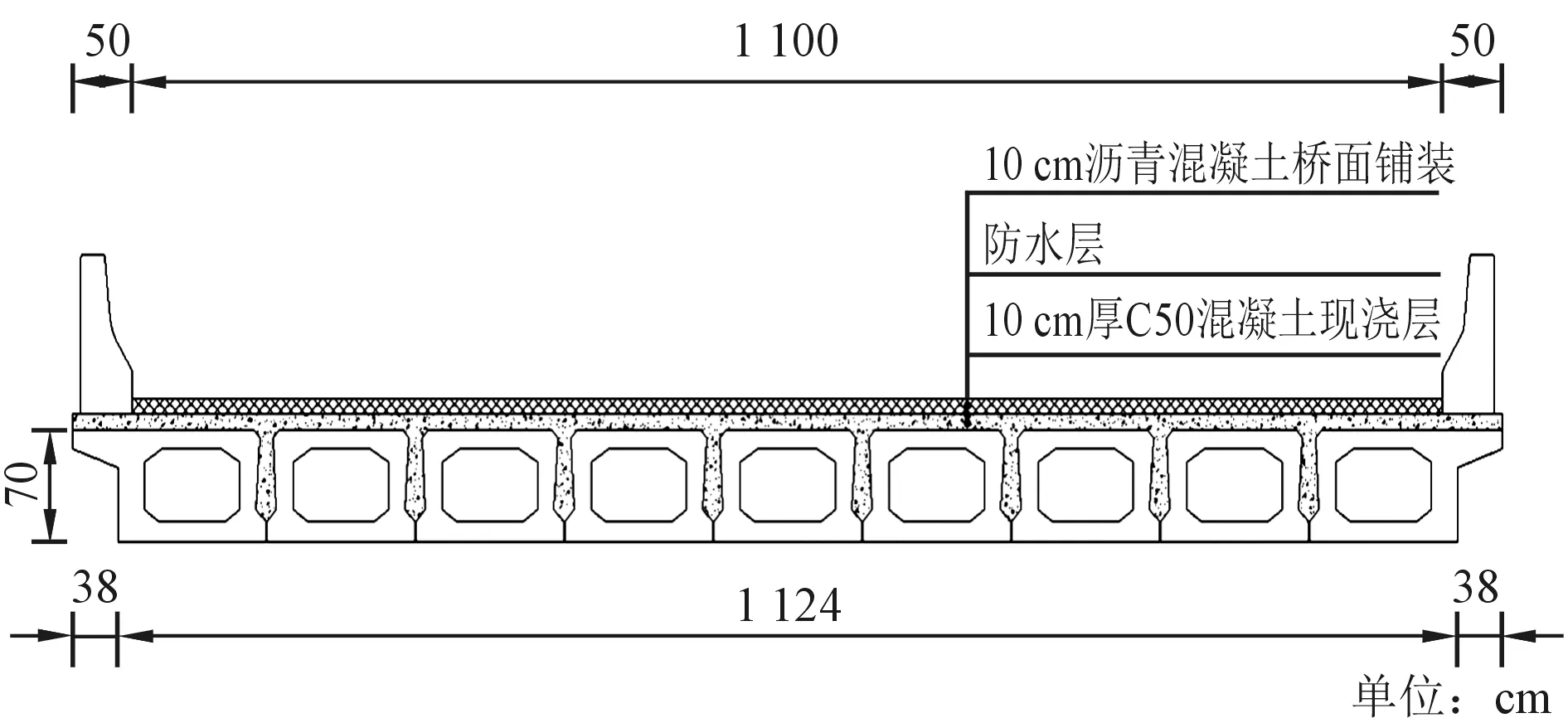
图2 传统13 m空心板桥横断面
采用本文所提出的新型铰缝对该桥横断面进行重新设计,如图3所示。将空心板间铰缝底部宽度由1 cm调整为20 cm,企口位置宽度由11 cm调整为40 cm;将原先空心板片数由9片调整为8片,边板翼缘挑臂由38 cm调整为34 cm,其他参数不变。
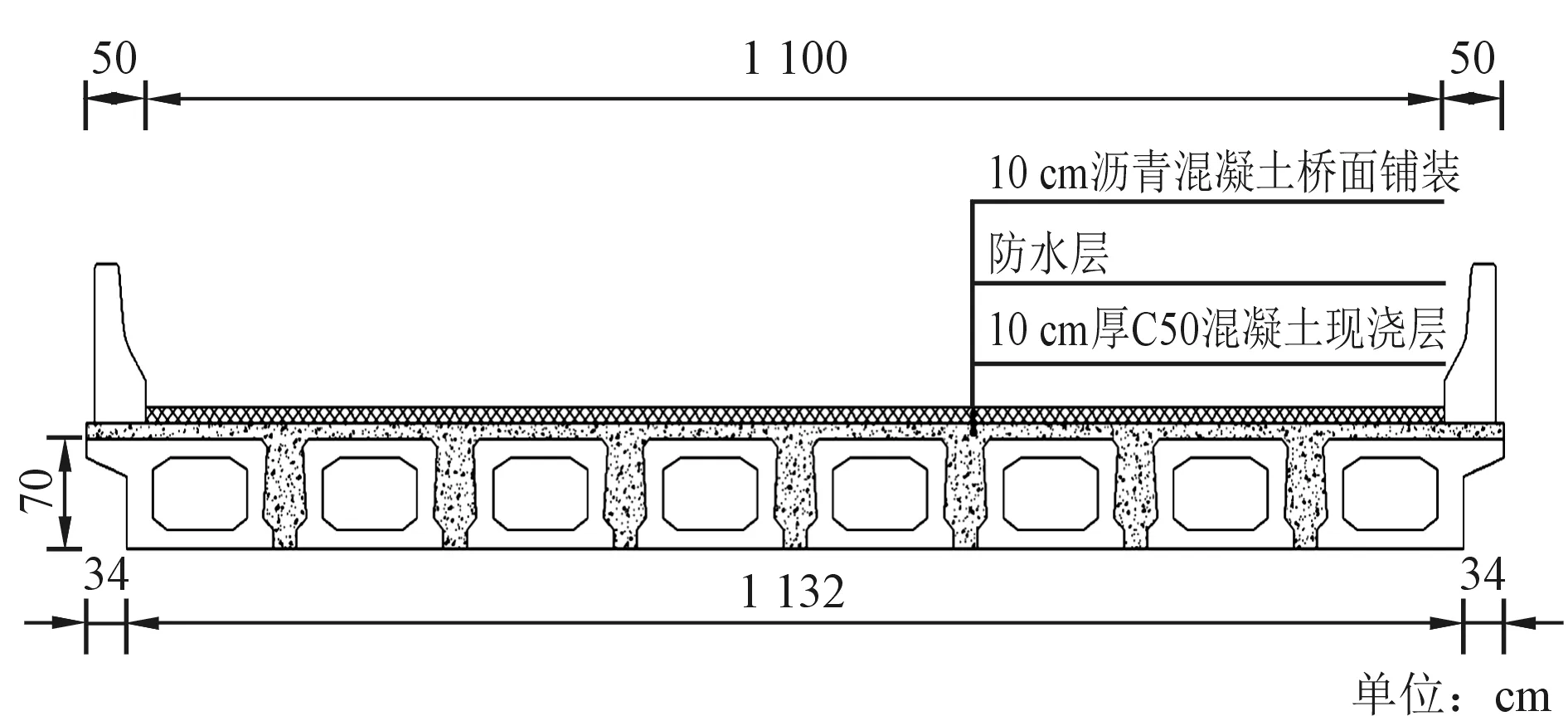
图3 采用新型铰缝的空心板桥横断面
2 三维有限元分析模型的建立
采用Midasfea六面体8节点单元建立空间分析模型。空心板桥共划分10 226个节点、80 080个单元,对两端支点位置和跨中的单元加密划分。本桥采用简支约束,单片空心板底共设4个支座,分析模型如图4所示,铰缝从左至右依次命名为1#~7#。
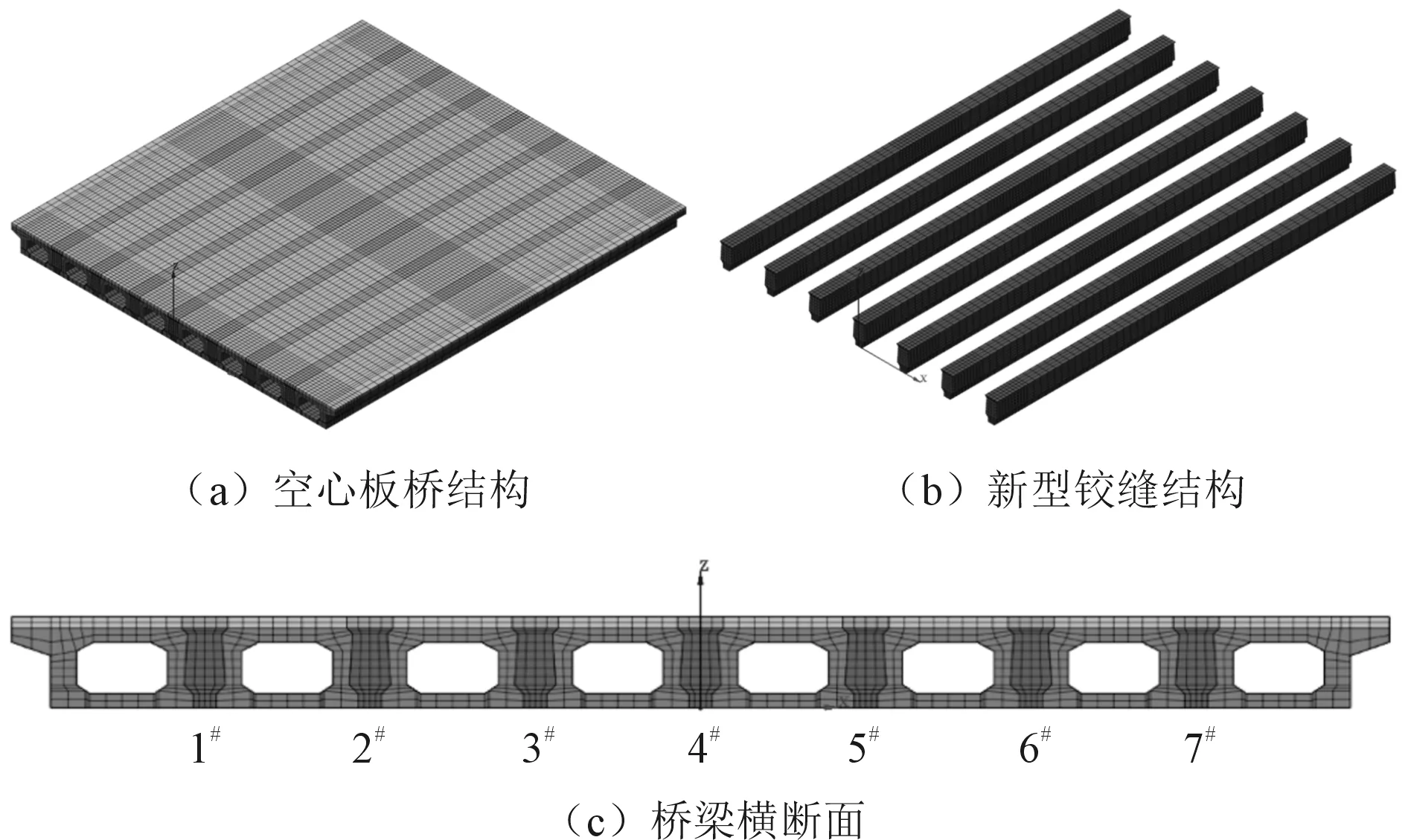
图4 计算分析模型
铰缝在浇筑完成后,在施工阶段主要受二期恒载和收缩徐变的作用,在运营期间主要受车辆荷载和温度梯度作用[12-14]。因此,本文考虑的主要荷载如下。
(1)二期恒载包含防撞墙和沥青铺装,防撞墙均布压力为16 kN·m-2,沥青铺装均布压力为2.4 kN·m-2。
(2)假定预制空心板的龄期为90 d,铰缝和桥面现浇层的龄期为3 d,计算空心板、铰缝和桥面板10年的收缩徐变差异。
(3)车辆荷载按照《公路桥涵设计通用规范》(JTG D60—2015)将双后轴对称施加于桥梁跨中,单个后轴车轮对桥面施加70 kN的节点集中力。
(4)温度梯度正温差按桥面板表面最高温度T1=14 ℃、桥面板以下100 mm处温度T2=5.5 ℃计算,反温差为正温差的0.5倍。
铰缝经历了施工阶段和运营阶段,因此计算分析主要考虑以下3个工况。
工况一:施工阶段。主要施工顺序为:吊装预制空心板(材料龄期90 d);浇筑铰缝和桥面现浇层(材料龄期3 d);施加二期恒载;完成3 650 d的收缩徐变发展。通过查看成桥10年后铰缝的受力情况,分析二期恒载和收缩徐变对铰缝受力的影响。
工况二:车辆荷载。该工况考虑了4种车辆荷载在横桥向的布置方式(图5):方式1,车辆对称居中布置,见图5(a);方式2,车辆布置于横桥向中部位置,一侧后轴作用于中间铰缝上,见图5(b);方式3,车辆布置于横桥向外侧位置,外侧后轴作用于最外侧铰缝上,见图5(c);方式4,车辆布置于横桥向最外侧位置,外侧后轴作用位置距离防撞墙50 cm,见图5(d)。
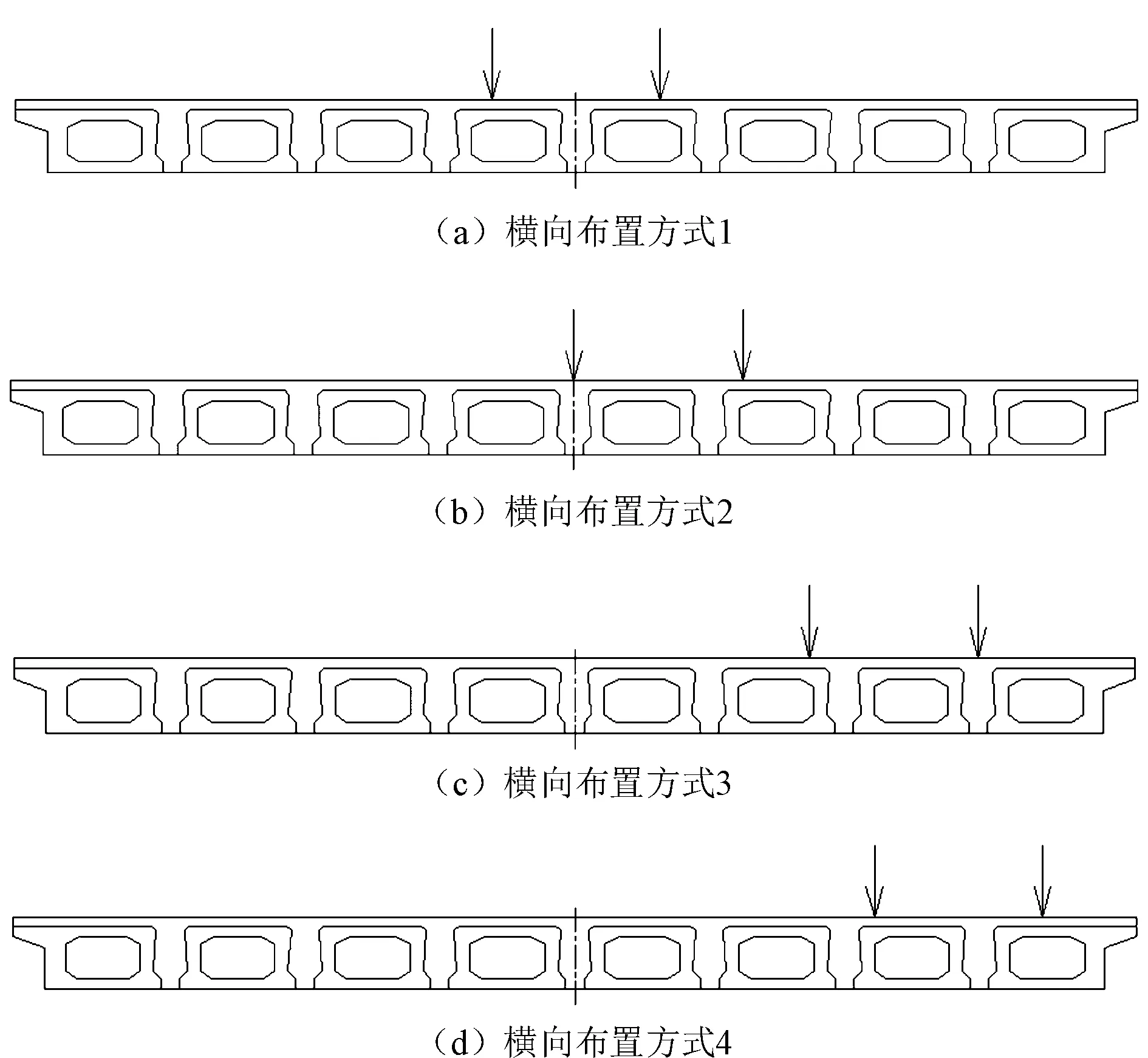
图5 四种车辆荷载横向布置方式
工况三:温度梯度。正温差使铰缝截面下缘产生压应力,而反温差在铰缝截面下缘产生拉应力,因此本次研究仅考察温度梯度反温差的效应。
根据《公路桥涵设计通用规范》中温度梯度效应的计算公式计算铰缝截面的受力。
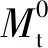
3 计算结果及分析
计算空心板在上述3种荷载工况作用下的受力,通过查看铰缝的纵桥向正应力,分析其受力特征,同时对铰缝跨中截面进行内力积分,用作此后的铰缝截面配筋设计。
3.1 施工阶段
完成预制空心板吊装后,浇筑铰缝和桥面现浇层,然后施加二期恒载,之后按3 650 d完成收缩徐变发展。在整个施工过程中,铰缝受到二期恒截、收缩徐变发展差异的作用。通过三维有限元分析模型进行计算。
图6为纵桥向正应力效应最大的7#铰缝受力云图,图中应力以受拉为正、受压为负。
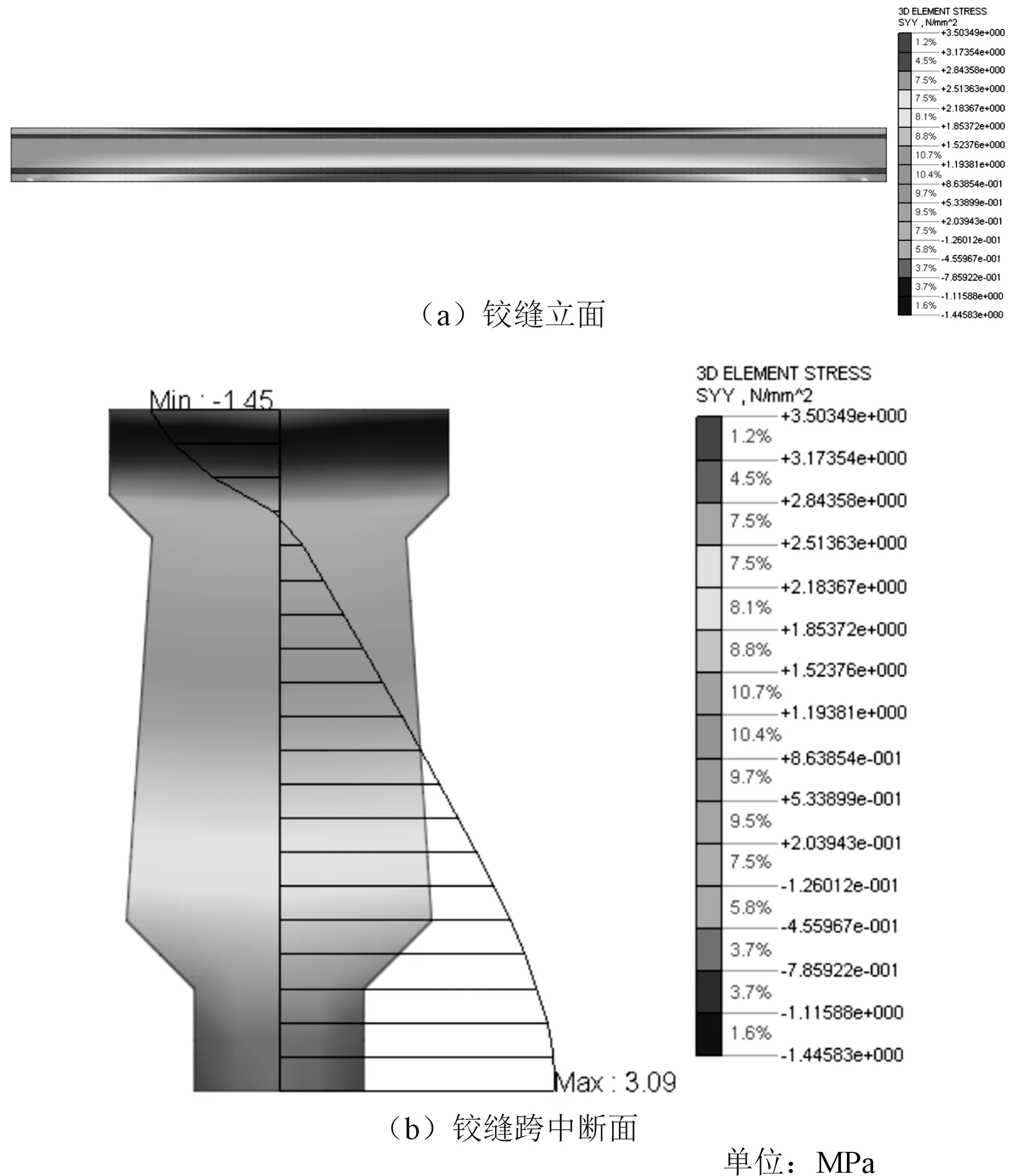
图6 工况一下7#铰缝的纵桥向正应力
从图6(a)可知,最大拉应力发生在铰缝跨中截面的下缘,为3.50 MPa,铰缝采用的混凝土标号为C50,其抗拉强度设计值为1.83 MPa;由图6(b)可知,铰缝基本处于受拉状态,受压基本依靠桥面现浇层,且铰缝底缘以上1/2高度范围内的拉力均超过抗拉强度设计值。
1#铰缝跨中截面下缘最大拉应力分别为:3.50 MPa;2#铰缝为3.37 MPa;3#铰缝为3.29 MPa;4#铰缝为3.26 MPa;5#铰缝为3.29 MPa;6#铰缝为3.37 MPa。桥梁跨中断面铰缝的最大拉应力均已超过铰缝混凝土的抗拉强度设计值,1#和7#铰缝是所有铰缝中受力最不利的铰缝。
为了对铰缝进行配筋设计,在Midasfea中定义一个垂直于纵桥向的跨中位置平面,通过在该平面的内力积分可得到铰缝的内力,图7为最不利铰缝7#铰缝的内力积分结果。
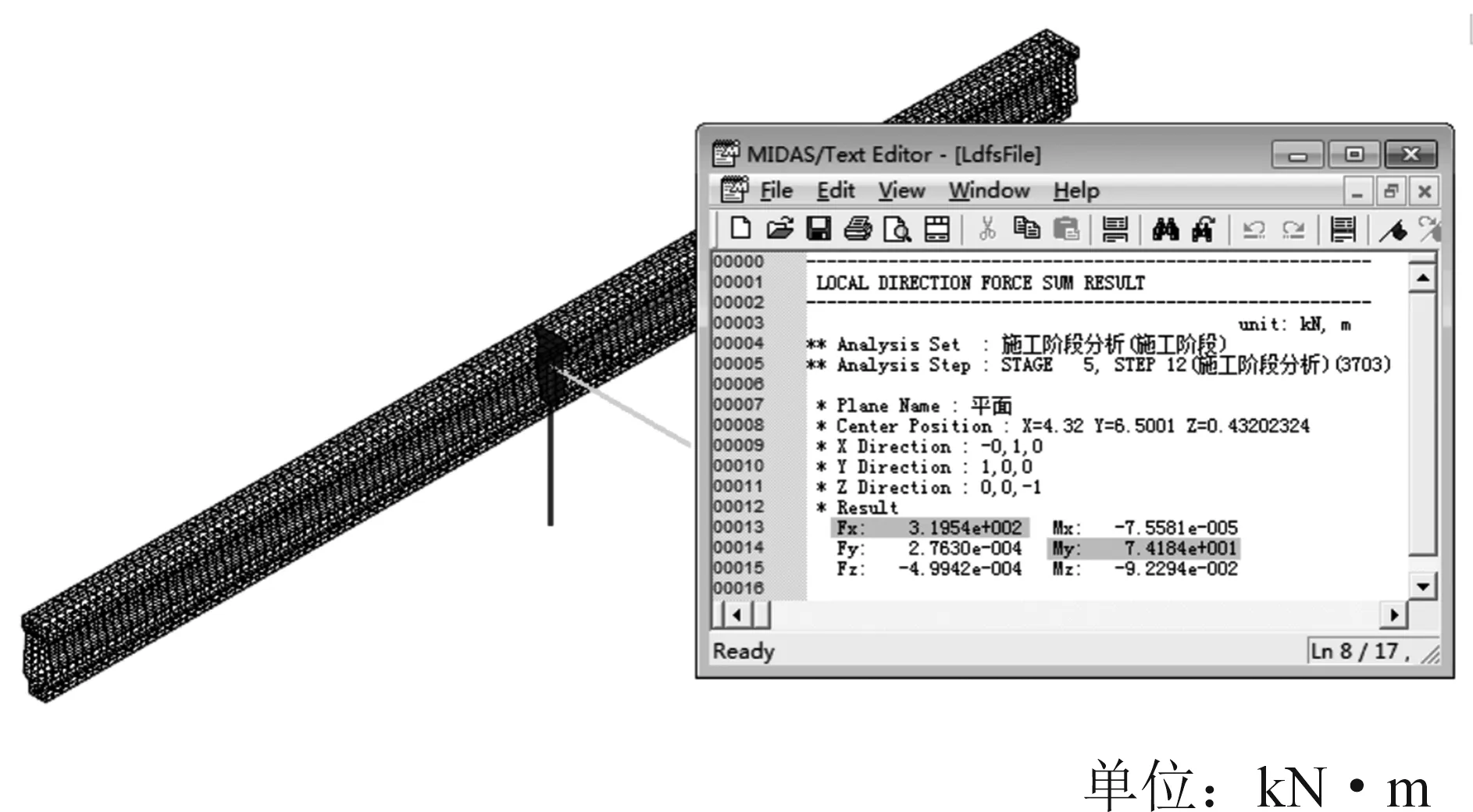
图7 工况一下7#铰缝内力积分
从内力积分结果可见,在施工阶段发展过程中,铰缝会承受较大的弯矩与拉力,处于拉弯的受力状态。铰缝受拉主要由空心板与铰缝存在的收缩徐变发展差异产生。
3.2 车辆荷载
通过对4种布载方式进行对比分析可知,车辆布载方式4作用下,7#铰缝跨中的纵桥向正应力最大,为1.40 MPa,见图8(a),此时7#铰缝跨中截面、底缘以上1/2高度范围均处于受拉状态,见图8(b)。
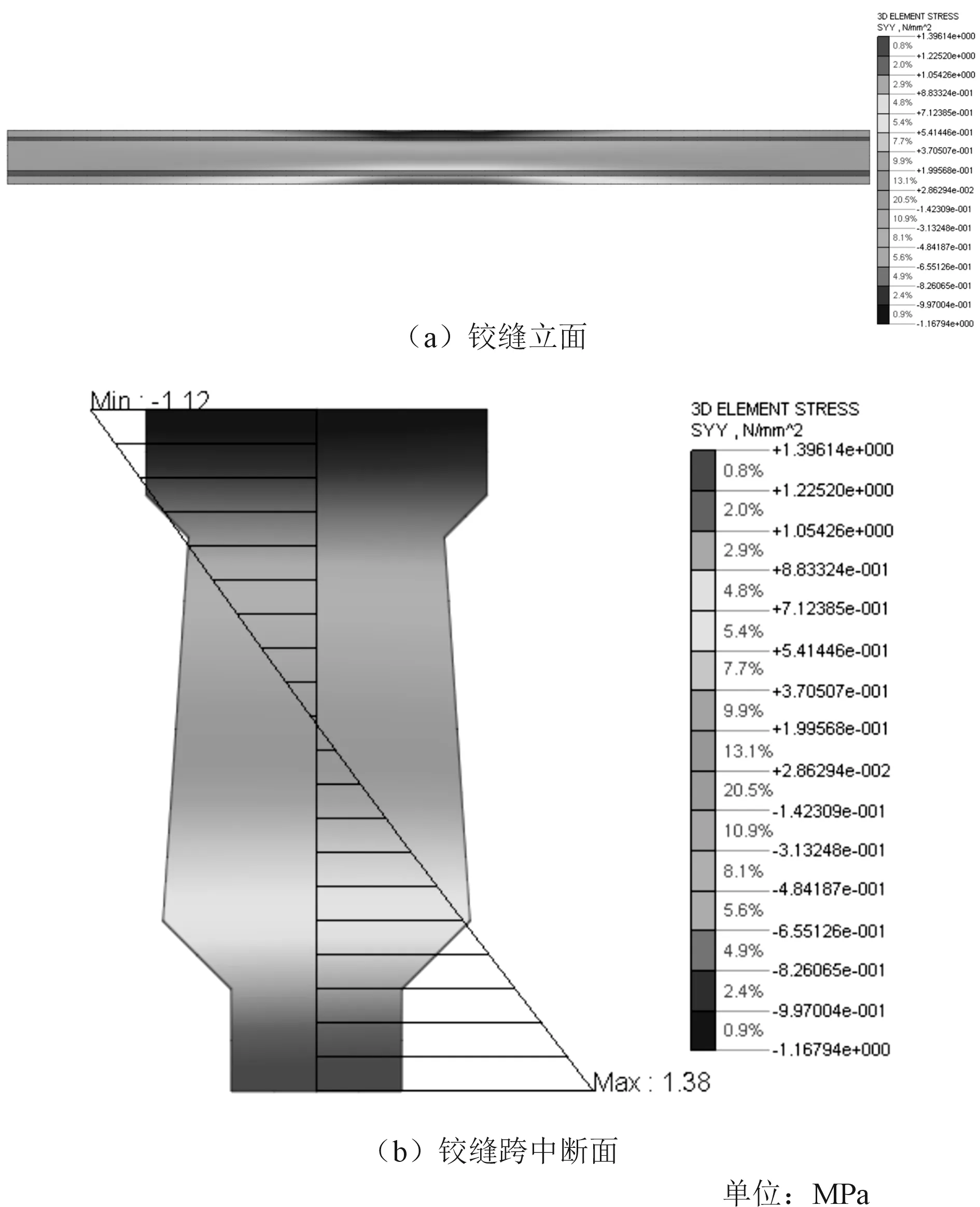
图8 布置方式4时7#铰缝的纵桥向正应力
同样,通过内力积分得到7#铰缝跨中截面的纵桥向弯矩值为40.10 kN·m,轴向拉力为2.94 kN。
3.3 温度梯度
根据式(1)~(3)计算得温度梯度作用时铰缝的纵桥向内力和正应力,结果如表1所示,表中应力正值为压应力,负值为拉应力。
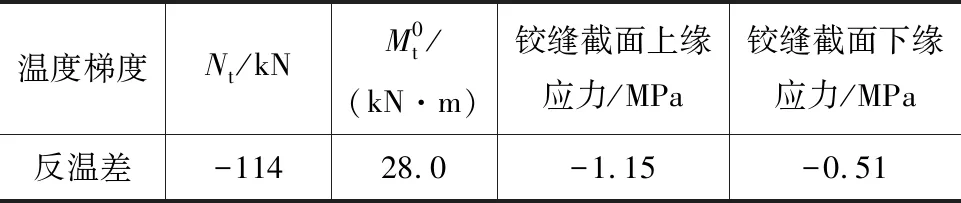
表1 温度梯度作用时铰缝的受力
由表1可知,反温差也会在铰缝截面下缘产生0.51 MPa的拉应力,其对应的轴力和弯矩都较大,且轴力为压应力。
4 铰缝的配筋设计
由上述计算结果可知,新型铰缝在上述二期恒载、收缩徐变、车辆荷载及温度梯度作用下,7#铰缝即最外侧铰缝是受力最不利的铰缝。
对7#铰缝按照上述方法进行内力提取并组合得:承载能力极限状态基本组合的设计弯矩值Md=184.38 kN·m,设计对应的轴向拉力Nd=224.40 kN;正常使用极限状态的长期效应组合轴力值Nl=274.40 kN,长期效应组合弯矩值Ml= 110.44 kN·m,短期效应组合轴力值Ns=240.20 kN,短期效应组合弯矩值Ms=121.87 kN·m。
按矩形截面进行计算,铰缝截面宽度取铰缝横向尺寸最小的底边尺寸,即b=200 mm。同时,考虑桥面板的贡献,截面高度取800 mm,在铰缝下缘配置纵向抗弯钢筋。
分别对铰缝进行抗弯和抗裂验算,结果表明,结构设计按抗裂控制设计,铰缝下缘需配置纵向抗弯钢筋的面积As=2 418 mm2。
根据计算结果,在铰缝截面下缘配置4C28的纵向受拉钢筋,As=2 463 mm2,由于铰缝宽度的限制,将纵向抗弯钢筋分2层布置,如图9所示。
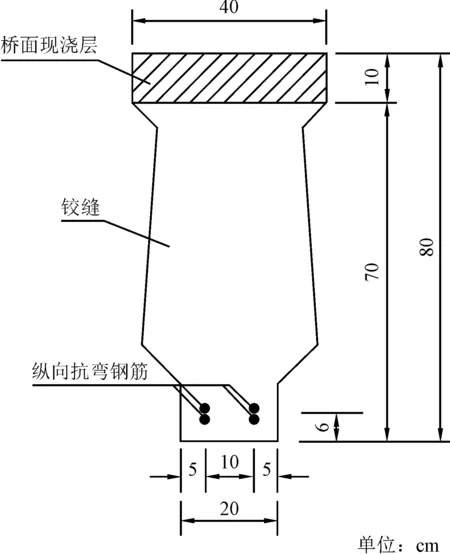
图9 铰缝纵向配筋设计
5 结 语
本文在对传统铰缝受力分析的基础上,提出了可克服其混凝土无法有效振捣、不具备抗弯和抗裂能力等技术缺陷的新型空心板铰缝,并通过建立Midasfea三维有限元分析模型,分析了新型空心板铰缝在完成施工、温度梯度及车辆荷载作用下的受力情况,同时在对应力结果进行内力积分后,对新型铰缝进行配筋。
(1)在二期恒载及考虑了空心板和铰缝的收缩徐变差异作用等条件下,铰缝中下部将产生可使铰缝开裂的拉应力;同样,车辆荷载、温度梯度反温差同样可使铰缝中下部产生拉应力。因此,铰缝在上述荷载作用下必然产生纵向裂缝,需要在铰缝内合理配置纵向钢筋。
(2)车辆荷载偏载为铰缝的最不利布载方式,此时受力最大的铰缝为最外侧铰缝。
(3)一般实体单元仅可给出应力结果,本文通过对实体单元进行内力积分,可提取得到所需的内力,从而进行配筋设计。
