振动及振荡压路机振动轴承摩擦功率计算方法探究
2019-04-15万汉驰
万汉驰
江苏骏马重工集团,江苏 靖江 214599
0 引言
振动压路机的钢轮在激振力的作用下产生振动,其振动功率的消耗主要在于维持钢轮的持续振动及振动轴承的摩擦功率损失,减振器的变形阻抗及车架的轻微振动也有少量的功率消耗.其中,维持钢轮持续振动所需的功率是主要部分,而振动轴承的摩擦功率损失是重要组成部分.
参考文献[1]中有关于振动(指圆周振动,下同)及振荡压路机的振动轴承摩擦功率损失的计算公式,其推导过程看似没有破绽,但结果却经不起推敲,笔者认为很是值得商榷,主要体现在以下3点.
(1)振动压路机振动轴承的摩擦功率损失计算公式为N2=2 μMgdf ,N2与μ、d及f成正比应该顺理成章,但其与振动轮参振质量M(原文中为md)成正比,而与振动轴(以下统称激振轴,有必要区分时称振动轴、振荡轴或垂直振动轴)的静偏心矩me无关,这一点让人无法理解,也是与实际不相符的.
(2)振荡压路机振动轴承的摩擦功率损失计算公式为N02=4π2μMA0d f3R/l(M原文中为md,l原文中为L),并且可以转化为N02=16π2μd f3me(按照参考文献[1]A0=4mel/MR),N02与μ、d及f3成正比同样顺理成章,与振动轴的静偏心矩me成正比也完全合乎情理,但与振荡轮的转动惯量J无关,这一点就让人无法理解了.
(3)计算示例中,同为工作质量10 t级的单钢轮振动压路机和振荡压路机(振荡压路机为在振动压路机主体上仅仅更换振荡轮而来),振动压路机振动轴承的摩擦功率消耗为1 780 W,而振荡压路机振动轴承的摩擦功率消耗为6 257 W,即单振荡轴振动轴承的摩擦功率消耗为3 129 W,是振动轴的1.76倍.问题在于,振动与振荡频率相同,单振荡轴的最大静偏心矩(即负载)为2.348 kg.m,只有振动轴最大静偏心矩5.568 kg.m的42%,说明振动轴承的摩擦功率消耗明显存在"倒挂"现象;尽管振动轴使用的是双列向心球面滚子轴承,而振荡轴使用的是直径较小的单列圆柱滚子轴承,但这种差异不足以造成如此大的反差.上述结果让人费解的同时,不得不怀疑计算公式的正确性.
其实进行简单的分析即可明了事情的"方向性"正确与谬误.振动轴承摩擦功率的损失,主要消耗在2个方面,其一为阻碍激振轴旋转,其二为轴承发热、滚道磨损及噪声等,那种仅仅理解为摩擦发热功率是十分片面的.对于具有大、小2种振幅的振动压路机,大振幅时振动轴承的发热量明显更大毋庸置疑,轴承内圈外滚道的磨损也更加严重(后文有述),轴承寿命也更短(计算振动轴承使用寿命时,一般用一半大振幅、一半小振幅进行负载组合,同样是这个道理)--这就是振动轴承摩擦功率消耗与激振轴静偏心矩(大、小振幅以及激振力的变化,其本质是激振轴静偏心矩的变化引起)相关的明证,而此时参振质量和振动频率等并没有改变.振荡压路机及垂直振动压路机亦然。

另一方面,对于振荡压路机而言,完全可以近似地将其平行的双振荡轴看成2根振动压路机的单振动轴,只是单振荡轴的静偏心矩只有单振动轴的50%左右罢了.因此可以简单地做出初步判断:振荡压路机单振荡轴振动轴承的摩擦功率损失一定小于同吨位振动压路机振动轴承的摩擦功率损失,30%~40%是可以接受的结果,因为这与振荡参数设计及振动轴承匹配有关;基于振动压路机各项匹配合理的前提下,甚至可以用30%~40%这一值反过来验证振荡压路机振动参数设计及振动轴承匹配的合理性.
本文从振动轴承的受力分析入手,简单推导了振动、振荡和垂直振动3种产品的振动轴承摩擦功率计算公式,并对计算结果展开对比与分析,这些都是基于振动为单激振轴(可以是通轴,也可以是左右联通的半轴,用双激振轴时将特别说明)、振荡及垂直振动为平行双轴(相当于两根振动轴,中间传动轴不在考虑之列)的轮子结构为前提.笔者在此长篇累牍地喋喋不休,将一个看似十分简单的问题解释得如此复杂,只是希望尽量"浅入浅出"地将问题分析透彻,在全方位自我解惑中真正探明究里,以达到避免以讹传讹的目的;尽管从本文分析与计算的结果来看,大部分数值相差并不大,但仍然具有理论和实践意义,更希望引起对此问题感兴趣者的共鸣和争鸣.压路机亦然.
1 振动轴承受力分析
1.1 分析样本确定
为了增强可比性,本文沿用了参考文献[1]中的10 t 单钢轮振动压路机(实际产品,也是参照基准)和10 t级单钢轮振荡压路机(实际产品)作为分析对象;并虚拟了同吨位的另外2个产品及其振动/振荡参数,使之基本具有"同口径"的特征.4种产品的相关参数见表1.
可以这样理解,4台完全相同的10 t单钢轮振动压路机(振动参数正常,即实际产品),通过更换钢轮的方式,将其中2台改制为振荡压路机(一台振荡参数稍小,即实际产品;另一台振荡参数正常,即虚拟产品),1台改制为垂直振动压路机(振动参数正常,即虚拟产品;实际产品的振动参数较虚拟产品稍大,但由于单钢轮垂直振动压路机主要压实厚铺层,一般实际工况中很少有10 t级的产品应用,故表1中未列出其实际产品).
所谓"同口径",主要指振动频率相同,保持参振质量不变,振荡和垂直振动压机单激振轴上的最大静偏心矩为振动压路机的一半,同时钢轮半径、2根平行双激振轴的间距等具体结构尺寸也必须相同,而钢轮的其它结构尺寸以及主要质量分布(涉及轮子的转动惯量)等,也应该尽量保持一致.
1.2 振动轴承受力分析
振动轮在地面振动的过程中存在3种外力,即激振力F0、参振质量(即钢轮质量,也称下车质量)引起的重力Mg和地面的摩擦阻力Mgφ(振动钢轮与地面的摩擦系数,可以用附着系数φ代替,而不能用滚动阻力系数fr代替,更不能两者同时都考虑,后文有述).振动轴承的正压力P属于振动轮整体系统的内力,是一个平均值,而且是指单激振轴上所有振动轴承的正压力之和(下同).要分析振动轴承的正压力P,就必须将激振轴、偏心块和振动轴承内圈作为一个施力分体即轴系(质量为m ),而将振动轴承外圈和振动轮体等作为一个受力分体即轮系(质量为M-m ,对平行双轴钢轮结构的振荡及垂直振动而言质量为M-2m ),这样振动轴承的正压力P就变成了2个分体之间的外力.振动轴承正压力P的构成,取决于3个外力的大小.
这里引入固定基础说、活动基础说和负载说3个名词.
固定基础说:当参振质量M足够大,即Mg>>F0且Mg>F0/φ时,参振质量M就相当于是一个质量足够大的"固定基础".此种情况下,无论轮体向哪个方向运动,振动轴承的正压力P都与激振力F0有关,而与Mg及φ无关.
负载说:这里所说的负载分为重力负载和摩擦阻力负载2种.当激振力F0足够大,即F0>>Mg时,振动轴承的正压力P主要取决于负载--轮体垂直向上运动时与重力负载Mg有关,轮体水平向左或向右运动时与摩擦阻力负载Mgφ有关,而只有在轮体垂直向下运动时才与激振力F0有关.
活动基础说:当参振质量M很大,即Mg>F0但Mg 很显然,无论是"基础说"还是"负载说",振动轴承的正压力永远遵循取施力(激振力F0)与负载(Mg或Mgφ)两者中的较小者.振动、振荡及垂直振动压路机,在一定程度上符合"负载说"的情形;参考文献[1]也是按照"负载说"分析的,只是对一些具体参数的理解和处理不同罢了. 下面基于各种假设条件(始终f≠0),以"剥笋"的方式进行解析. 基于"固定基础说"时 上述2式中θ值为激振力向上离开水平轴线的夹角,在2π范围内对其进行积分即可得到振动轴承的正压力平均值. 1.2.1 振动状态 为了简化问题,假设钢轮处于静止状态(不滚动,下同),其受力情况如图1所示. 这里也采取"剥笋"的方式进行分析. (3)假设F0≠0、m =0:当激振力垂直向上时,由于Mg为重力负载,即P=Mg,相当于取F0与Mg中的小者;当激振力水平向左或向右时,由于轮体与地面的摩擦力成为阻力负载,即P=Mgφ;当激振力垂直向下时,由于轮体支撑于地面,即P=F0. 当激振力水平向左图1(b)或向右图1(d)时,激振力使得轮体沿水平方向运动,而轮体与地面之间的摩擦力则形成负载的反作用力,摩擦系数可以用附着系数代替,即P=Mgφ.由于附着系数又随压实状态不同而变化,而本文计算的是最大功率消耗,因此可以用初始压实时的附着系数(取值0.3)代替.这里并未考虑上车质量(M M )的影响(后文有述). 当激振力垂直向下图1(c)时,相当于地面成为轮子的支承,与轮体对激振轴系形成反作用力,则P=F0+m g. 由于激振力是循环变化的,导致振动轴承的正压力也是循环变化的,但可以求得其最大值和平均值.如图2所示,振动轴承的正压力为按周期2π呈弦高不等、4个半波的正弦曲线,因此可以用4个方向的平均值代替,并在2π范围内进行积分,即可得到: 需要特别说明的是,由于F0为单根激振轴的激振力,因此P为单根激振轴上所有振动轴承所承受的正压力之和的平均值(简称正压力,下同),而并非单个振动轴承所承受的正压力. 1.2.2 振荡状态 振荡轮的受力情况如图3所示. 需要说明一点,其实一般振荡机构为三轴机构,除平行布置的2根振荡轴以外,还有作为传递动力的中间传动轴,但由于载荷很小,轴承摩擦功率消耗也很小,在此忽略.垂直振动机构亦然. 当图3(b)、图3(d)中激振力处于水平向左或向右时,激荡力偶矩使得钢轮沿弧线方向产生扭动,这一激荡力偶矩需要克服钢轮与地面之间的摩擦阻力矩及自身的转动惯性阻力矩,摩擦系数可以用附着系数代替,即P1=P2=P,PL=MgφR+Jg/R,故P=MgφR/L+Jg/RL.由于滚动阻力系数又随压实状态不同而变化,而本文计算的时最大功率消耗,因此可以用初始压实时的滚动阻力系数(取值0.3)代替. 同样地,由于激荡力偶矩是循环变化的,导致振动轴承的正压力也是循环变化大,因此振动轴承的正压力可以用4个方向平均值代替,并在2π范围内对振动轴承的正压力平均值进行积分,可以得到置亦然. 1.2.3 垂直振动状态 g及激振力F0的作用力点为振荡轴中心O1或O2,振动轴承正压力P1及P2的作用力点为振动轴承滚动体中心O . 当激振力处于水平方向图4(b)、图4(d)时,地面支承钢轮重力,则P1=P2=F0,但2组激振轴上轴承正压力的方向相反.严格来讲,P应为F0与m g的合成即两者的平方和的开平方,而且P1与P2呈左右镜像关系,在此作简化处理;当激振力垂直向下图4(c)时,地面作为支承,则P1=P2=F0+m g. 当振荡轮中两根激振轴处于水平平面内时,可以得到相同的振动轴承正压力4个方向的平均值.其他任意位 同样,由于激振力是循环变化的,导致振动轴承的正压力也是循环变化大,因此振动轴承的正压力可以用4个方向平均值代替,并在2π范围内对振动轴承的正压力平均值进行积分,可以得到 1.2.4 关于振动加速度的讨论 区别于上述振动、振荡及垂直振动压路机"负载说"的是"加速度说",同样可以按照激振力在四个特殊方向时对振动轴承产生的正压力进行分析. 对于振动轮(设振动加速度为a)有以下几种情况. (1)当F0垂直向上时(图1(a)). 对振动轴承在4个典型方向的正压力求取平均值,并在2π范围内进行积分,可以得到 (3)当F0水平向左或向右时(图4(b)或图4(d)),P左=P右=F0. 对振动轴承在上述4个典型方向的正压力求取平均值,并在2π范围内进行积分,可以得到: 需要说明的是,如果按照参考文献[1]中振动轮(同轴结构)的分析逻辑,由于水平振动钢轮根本就没有垂直方向的运动,则振动轴承的正压力为0,因而就没有振动轴承摩擦功率消耗这么一档子事;而按照振荡轮(平行双轴结构)的分析逻辑,则振动轴承的正压力为P=2F0/π,与振荡轮一样,只是在推导振荡轮振动轴承摩擦功率消耗时进行了一系列"辗转腾挪"的变化而已,从而使其与参振质量M或名义振幅A0建立关系,明显存在"生拉硬扯"的嫌疑,最终必然导致本来十分清晰的计算式变得"面目全非". 由此看来,水平振动轮这一"旁证"在无意之中证明了本文的"负载说"和参考文献[1]中关于振动轴承摩擦功率分析逻辑和计算式的"不靠谱". 某一轴承的摩擦消耗功率式中:P为该轴承所受的径向力即正压力(N);μ为该轴承的摩擦系数,单列滚子轴承取μ=0.005,双列滚子轴承取μ=0.007;ω为该轴承的旋转角速度(rad.s-1);d为该轴承的平均直径(m). 对单激振轴而言,可以是通轴,也可以是联通的两个或多个半轴,若其上振动轴承的总数量为n(假设规格相同),则单激振轴上所有振动轴承的摩擦功率消耗为nN;设单激振轴上所有振动轴承的正压力之和为P,则每一个振动轴承的正压力为P/n. 那么,单激振轴上所有振动轴承的摩擦功率消耗式中: P为单激振轴上所有振动轴承所受的正压力之和(N);f为激振轴的振动频率(Hz). 从式(7)可以看出,单激振轴的振动轴承摩擦功率消耗与激振轴上的振动轴承数量无关,而整个钢轮的振动轴承摩擦功率消耗与激振轴组数成正比,并且其核心是如何计算振动轴承的正压力P值.另一方面,以上所述均是对单个振动或振荡轮而言,双钢轮振动或振荡压路机则需要加倍,或者单独计算两个轮子的振动轴承摩擦消耗功率,然后求和. 基于"负载说"时,将式(1)、式(2)和式(3)分别代入式(7),可以得出3种振动方式下的单激振轴上振动轴承摩擦功率消耗计算式,即 在所有参数中,由于质量参数、尺寸参数等为不变量,静偏心矩、振动频率等虽然可以调节,但都属于自变量,而名义振幅/荡幅、激振力等为因变量.按理在最终计算公式中都必须以不变量和自变量表示,但由于表1中已经列出了所有不变量、自变量和因变量的数值,故在此以最简洁的表达式显示. 将表1中的相关数据代入式(8)、式(9)和式(10),即可得"负载说"下各产品的振动轴承摩擦功率消耗值,见表2.需要说明的是,在不影响原公式表达含义的基础上,所有计算式中已将相关参数符号进行了统一. 同理,基于"加速度说"时,亦可得各产品的振动轴承摩擦功率消耗值,见表2. 为了进行对比,也将参考文献[1]的计算方法及计算结果列入表2中.需要说明一点,参考文献[1]中振荡轮的振动轴承正压力原为P=2πMA0f 2R/l,根据其A0=4mel/MR,可转化为P=2F0/π(其实就是参考文献[1]中的初始结果),表2中即以此式代入. 从表2中可以看出,振动(同轴结构钢轮)单激振轴上的振动轴承正压力为P=2Mg/π,垂直振动(平行双轴结构钢轮)单激振轴上的振动轴承正压力为P=Mg/π;如果分析平行双轴结构振动轮及单轴结构垂直振动轮的话,其单激振轴上的振动轴承正压力分别为P=Mg/π和P=2Mg/π;唯独振荡(平行双轴结构钢轮)单激振轴上的振动轴承正压力为P=2F0/π,在"五人帮"中显得如此"格格不入".判断对错的道理很简单,不是其中1人错误,就是另外4人不正确,或者5人都有问题;因此,"直觉上"让人不得不怀疑参考文献[1]中关于振动轴承摩擦功率计算方法的正确性. 正如前文在"剥笋"中的解析,当m ≠0、F0=0时(即无静偏心矩的光轴),振动轴承的正压力P=m g,此时振动系统的功率消耗N振等于振动轴承的摩擦功率消耗,即N振=N摩=πμdm ≠0、F0≠0时(即激振轴的静偏心矩为me),振动系统的功率消耗为在上述F0=0的基础上增加了克服激振轴惯性矩而需要消耗的功率N惯(N惯=2πmeg f),即N振g f .当m =N摩+N惯;而且同时发生了一系列的变化,即振动轴承的正压力因为F0的作用而增加(摩擦功率消耗由N摩=πμdm =πμdPf),钢轮会产生振动(消耗功率N下),减振器也会发热(消耗功率N减),机架也会产生振动(消耗功率N上);此时振动系统的功率消耗N振g f 增加至N摩+N下+N减+N上.由此可见,N惯的消耗不仅导致了N下、N减和N上的发生,而且使得N摩的消耗增加至N摩=N摩+N惯=N摩,最终使得振动系统的功率消耗N振大幅增加至N振.所以N摩只与M相关、而与me或F0无关肯定是错误的.姑且在此作个初步结论,下面将展开详细分析. 对计算结果进行分析和讨论,可以得到更多有用的信息. 3.1.1 本文计算数值分析 从表2所列本文计算的结果,可以看出以下几点. (1)振动实际产品的振动轴承正压力为39 481 N,而振荡实际产品、虚拟产品和垂直振动虚拟产品的振动轴承正压力分别为35 709、40 202 N和49 729 N,四者相差不大;这一结果与各自激振轴上的负载(静偏心矩或激振力)是不成比例的,尤其是振动实际产品的振动轴承正压力太过偏小,也不支持后三者使用额定动负荷较低的振动轴承的现实.因此说,振动实际产品振动轴承正压力的"绝对值"(指数值大小,下同)不合理,4种产品振动轴承正压力的"相对值"(指数值大小顺序和比例,下同)也不合理. (2)振荡与振动产品相比 振荡压路机单激振轴振动轴承的摩擦功率消耗(实际产品2 103 W、虚拟产品2 368 W)比振动实际产品(3 451 W)小,但双激振轴的合计值比振动实际产品大.这一点从直观上很容易理解,因为可以将振荡压路机的单激振轴视同一个静偏心矩减半的振动轴(这也是振荡轮可以使用较小规格和承载能力振动轴承的原因),但由于振动轴承数量增加了一倍,因此振荡轮中全部振动轴承的摩擦功率消耗必然会大于振动压路机(尽管与振动轴承数量没有关系,但毕竟增加了摩擦环节). 垂直振动与振动产品相比 垂直振动压路机虚拟产品的单激振轴(振动参数已按同口径要求设置)振动轴承的摩擦功率消耗(2 929 W)也比振动实际产品(3 451 W)小,但双激振轴的合计值比振动实际产品大,而且是四者中的最大者,这一点从直观上同样也很容易理解. 由此说,不考虑振动轴承的影响因素时,直观上4种产品振动轴承的摩擦功率消耗"相对值"似乎是合理的;但其"绝对值"因振动轴承正压力"绝对值"的不合理而不合理.这是宏观上的判断. (3)可以假设2种虚拟产品使用与振动压路机完全相同的振动轴承,即排除振动轴承的影响因素,这是另一种"同口径"之法,即考虑振动轴承不同引起的差异系数0.132 5X0.007/0.125X0.005=1.484,那么2种虚拟产品单激振轴振动轴承的摩擦功率消耗2 368 W和2 929 W可以分别转化为3 514 W和4 347 W,两者均已大于振动实际产品的3 451 W,形成了"倒挂"现象.也就是说,在所有参数相同(包括振动参数和振动轴承参数)的情况下,无论是理论上、还是直观上判断,振荡和垂直振动产品单根振动轴的静偏心矩为振动产品的一半,其振动轴承的摩擦功率消耗也应该为振动产品的一半左右;但结果显示振荡和垂直振动虚拟产品单激振轴振动轴承的摩擦功率消耗却大于振动轮,即"相对值"是完全不合理的.这是偏于微观上的判断. 由此看来,利用"负载说"计算的振动轴承正压力和摩擦功率消耗,无论是"绝对值"还是"相对值"都是不合理的,说明这种方法不足采信. 3.1.2 参考文献[1]计算数值分析 回过头再来关注一下参考文献[1]中相关计算数据中隐藏的悖论. (1)振动实际产品的振动轴承正压力P为19 985 N,单个振动轴承所承受的正压力则为其四分之一即4 996 N,约500 kg,明显小得太过离谱.要知道钢轮之所以产生振动,是因为激振力F0的缘故,而F0是通过振动轴承以正压力P的方式传递至钢轮的,所以P值不可能很小,否则钢轮振动不起来;另外,难道计算振动轴承的使用寿命时是将此值作为动负载考虑的吗?显然不是.而且,振荡实际产品和虚拟产品的振动轴承正压力分别为53 113 N和62 976 N,分别是振动实际产品的2.66倍和3.15倍,难道使用额定动负荷小得多的NJ316EC轴承可以保证要求的使用寿命吗?而实际情况是无论振动还是振荡实际产品,振动轴承的匹配还是比较合理的. 如果关注垂直振动产品的相关数据,就会发现结果更加匪夷所思,但不必怀疑笔者按照参考文献[1]中分析振动产品的思路推算出来的垂直振动产品振动轴承摩擦功率计算公式的正确性(当然前提是振动产品的振动轴承摩擦功率分析思路和计算公式是正确的).因此只作参考,一概不进行分析. (2)振荡压路机实际产品单激振轴上的振动轴承摩擦功率消耗为3 129 W,是振动实际产品整体值(1 747 W)的1.79倍,而振荡双激振轴的合计值则是振动实际产品整体值约3.58倍,这一结果完全让人不可理解,而且还没有考虑振动轴承差异系数引起的摩擦功率的节省效果(前文有述).如果对比振动参数同口径的振荡压路机虚拟产品,则振荡单激振轴、双激振轴上的振动轴承摩擦功率消耗分别是振动实际产品整体值的2.12倍和4.25倍,就更加不可思议了,可以说根本存在"方向性"错误.因此,参考文献[1]的计算方法和结果是不可信的,其根源在于同样是以"负载说"为理论基础,只是有一些具体细节处理略有不同罢了;这也是将此内容置于"负载说"一节下讨论的原因. (3)另外,参考文献[1]的"激振器的计算实例"一节中,在按大振幅工作时间100%校核振动压路机振动轴承的工作寿命时,单个振动轴承的动负荷是按照最大激振力进行平均分配,并考虑平衡系数γ得到的,即P=F0/nγ=197 840/(4X0.95)=52 063 N(参考文献[1]的计算实例中,F0为197 195 N,计算结果为46 834 N;但γ为乘积关系,应该是一处"硬伤".γ是指激振轴上各振动轴承承受的正压力不一致的修正系数,从受力角度考虑应该是一个放大系数,称之为不平衡系数似乎更加确切一些,并取值1.05时才应该是乘积关系),与4 996 N相差10倍之巨,说明参考文献[1]存在前后矛盾、不能自圆其说之处. (4)从表2中还可以发现一个规律,即激振轴上所有振动轴承的正压力之和P与该激振轴的激振力F0的关系.基于本文"加速度说"时,P≈(0.60~0.63)F0,适用于振动、振荡和垂直振动3种振动型式;而参考文献[1]的计算结果显示,振动时P≈(0.08~0.10)F0,振荡时P≈(0.60~0.63)F0,垂直振动时P≈(0.08~0.10)F0;而且这种关系不仅可以扩展到其他吨位的单钢轮振动压路机上,也同样适用于双钢轮振动压路机.可以这样理解,参考文献[1]明显存在"厚此薄彼"的嫌疑,而且这种"云泥之别"发生在计算振动轴承正压力这一"源头"上,必然造成后续振动轴承摩擦功率计算结果的失真. 由此可见,参考文献[1]中关于振动轴承正压力和摩擦功率消耗的计算方法及结果是不可信的. 3.2.1 振动加速度说计算与分析 根据"关于振动加速度的讨论"一节中的相关公式,可以进一步计算出4种产品的振动轮/振荡轮在4个典型方向的振动加速度值,见表3.毫无疑问,表3中所列加速度值是符合实际情况的,因而也是合理的. 钢轮的振动加速度还有另外一种计算方法,即a=A0ω2/g;对表3中振动实际产品而言,a=6.30g.需要说明的是,这与表3中的计算值并不矛盾,因为钢轮振动在每一个Hz过程内并不是等加速度的;或者说振动过程中钢轮轴线的位移轨迹不是一个正规的圆,而是一个左右短轴相等(加速度为6.00g)、上半长轴(加速度为5.30g)大于下半长轴(加速度为7.30g)的非正规椭圆.而以A0ω2/g计算钢轮振动加速度是基于钢轮悬空振动为前提的,而且是一个均值;令计算式中φ=0可得a右=a左=6.30g,那么4个方向的平均值即为6.30g,两者是完全吻合的. 鉴于加速度计算值符合实际情况这一基本事实,加上在考虑振动轴承差异系数后的单激振轴摩擦功率消耗的"相对值"的合理性,可以判断"加速度说"是基本可以采信的. 3.2.2 振动轴承正压力和摩擦功率消耗数值分析 根据表2中所列计算的结果可以发现以下几点. (1)从单激振轴振动轴承的正压力方面考虑,4种产品分别为120 185、52 596、62 314 N和61 498 N,与其各自的负载(静偏心矩或激振力)的比值分别为0.607、0.630、0.630和0.622,这4个比值相当接近,并且实践证明也与各自的振动轴承规格匹配及实际使用寿命相适应,说明振动轴承正压力的计算方法不存在原则性问题. (2)从振动轴承摩擦功率消耗角度出发,振荡和垂直振动3种产品的双轴振动轴承摩擦功率消耗分别为2X3 098 W、2X3 671 W和2X3 623 W,均小于振动实际产品的10 506 W,这与"振荡压路机和垂直振动压路机较振动压路机节省振动功率"的现实情况是一致的. 振荡压路机与振动压路机相比节省振动功率(按照参考文献[1]中计算例题的计算结果为实际产品节省33.6%、虚拟产品节省18.9%),这是不争的事实;但以前普遍认为主要表现在节省维持钢轮振动的功率消耗方面(按照参考文献[1]中计算例题的计算结果为实际产品节省61.3%、虚拟产品节省51.5%),而不是节省振动轴承摩擦功率消耗(按照参考文献[1]的计算结果为实际产品多耗费251.5%、虚拟产品多耗费316.2%),垂直振动压路机也是如此.从"负载说"计算的结果来看,似乎"强烈"支持这一结论,即振荡压路机是更加耗费振动轴承摩擦功率的(按照本文的计算结果为实际产品多耗费21.2%、虚拟产品多耗费37.2%),且其中尚未考虑振荡轮中间传动轴的轴承摩擦功率消耗.而"加速度说"的计算结果则恰恰相反,即振荡压路机与振动压路机相比节省的振动功率主要表现在节省振动轴承摩擦功率消耗方面(按照本文的计算结果为实际产品节省41.0%、虚拟产品节省30.1%).不管真相到底如何,但肯定不能将"振荡压路机节省振动功率"与"振荡压路机节省振动轴承摩擦功率消耗"两者混为一谈;尽管真相可能确实是"振荡压路机节省振动功率主要、甚至全部是节省振动轴承摩擦功率消耗",但在此时下结论还为时尚早,还需要对振动功率展开详细分析(他文有述). (3)当同样考虑振动轴承不同引起的差异系数1.484时,振荡和垂直振动虚拟产品单激振轴的摩擦功率消耗3 671 W和3 623 W可以分别转化为5 448 W和5 377 W,均约为振动产品的10 506 W的50%左右.也就是说,在所有参数相同(包括振动参数和振动轴承参数)的情况下,振荡轮和垂直振动轮中单根振动轴的静偏心矩为振动轮的一半,它们的振动轴承摩擦功率消耗也约为振动轮的一半,而这一"相对值"是十分合理的,即振动产品摩擦功率消耗异常"飙高"(其实并不异常)主要是由于振动轴承差异造成的. (4)进一步地,在此可以逆向假设一下(并不是凭空臆断,最新的中小吨位单钢轮振动压路机以及双钢轮振动压路机大多已采用短圆柱滚子轴承),振动实际产品匹配使用NJ320EC振动轴承(额定动负荷391 kN、平均直径0.157 5 m、滚动摩擦系数0.005),在保证基本额定寿命满足要求的前提下,其振动轴承摩擦功率消耗将由10 506 W降低至8 920 W,降低了15%;但与振荡和垂直振动3种产品合理的大小顺序关系并没有改变,即"相对值"仍然是合理的. (5)需要进一步解释的是振动轴承摩擦功率消耗数值明显偏大(主要是振动产品)的问题,因为这么大的功率消耗不可能全部转化为发热、滚道磨损及噪音等,惟一合理的解释就是摩擦功率消耗的一部分阻碍激振轴的旋转,另一部分转化为热量、滚道磨损及噪音等.究其根源正是因为振动轴承摩擦阻力的存在,才需要持续消耗功率以克服摩擦力形成的阻力矩,从而维持激振轴的持续旋转,也才会持续地产生热量、滚道磨损及噪音等;如果消耗的功率全部用于振动轴承产生热量、滚道磨损及噪音等,那么即使是无静偏心矩的光轴,也不能始终保持旋转状态.其实任何摩擦都是如此,摩擦系数μ真是一个很"神奇的存在"--以"擅长"方向变化的摩擦阻力或阻力矩的方式,在摩擦功率消耗与摩擦发热、磨损及噪声等之间"左右逢源"并起着"承上启下"的作用;但摩擦消耗的功率中到底有多少转化成了热量、磨损及噪声等,是一个很难说清楚的事情,说不清楚的事情就不要强求--"水至清则无鱼",需要糊涂的时候就糊涂一把好了.笔者认为,在一般的振动压路机钢轮中,约有1/10左右的摩擦功率消耗在振动轴承的发热、滚道磨损及噪音等方面是一个比较合理的估计. (6)另外一项也需要解释,即在2个虚拟产品中(振动参数和振动轴承完全同口径),垂直振动压路机单激振轴振动轴承摩擦功率消耗(3 623 W)比振荡压路机(3 671 W)略小一些,这与人们对实际产品的感知并不相符.在实际工作中,振荡压路机主要用于压实薄铺层,而垂直振动压路机主要用于压实厚铺层;那么,人们的直觉自然是"干重活"的垂直振动压路机所消耗的振动功率肯定大于"干轻活"的振荡压路机(同吨位、同型式的产品).其实,产生这种"错觉"的原因在于一切是为了"同口径"对比--就单激振轴振动轴承摩擦功率消耗而言,3 671 W的振荡压路机是比实际产品的振动参数加大以后的虚拟产品,而3 623 W的垂直振动压路机却是比实际产品的振动参数缩小以后的虚拟产品,如果转换至两者的实际产品时将会出现"此消彼长"的情况(后文有述),那样就完全符合人们的感知了. 其实,任何过多的解释都是苍白无力的,数据才最具有说服力.在振动参数和振动轴承完全"同口径"的前提下,垂直振动压路机单激振轴上振动轴承消耗的摩擦功率就是比振荡压路机略低,这无需任何解释;如果结果是相反的(略高),同样不需要任何解释,只要"不离谱"就是正常的. 综上所述,从轴系角度出发,静偏心矩是负载,振动轴承的摩擦阻力也是负载;无论是振动、振荡还是垂直振动型式,激振轴都在以相同的频率旋转,振动轴承的受力方式都是一样的,故振动系统消耗的功率只与激振轴的负载相关.也就是说,在各种参数(振动参数及振动轴承参数)严格"同口径"对比的前提下,各种振动型式其振动系统消耗的功率应该是基本相当的.而在实际产品应用中,影响振动、振荡及垂直振动压路机振动系统功率消耗的因素,除振动参数设计配置的差异以外(如表1中的实际产品与虚拟产品的不同),更加主要的是振动轴承的设计配置不同--因为振荡及垂直振动单激振轴上的静偏心矩只有振动的1/2,因此可以使用较小规格的轴承,甚至还可以在现有实际产品的基础上再减小2个至3个规格而进一步降低振动轴承摩擦功率消耗,这是从振动轴承"摩擦功率"角度造成振荡及垂直振动与振动压路机相比节省功率的原因. 而从轮系角度出发,参振质量是负载,钢轮与地面的附着系数产生的摩擦阻力也是负载,而振动轴承的摩擦阻力属于内力;于是似乎可以将振荡压路机及垂直振动压路机的钢轮简单地看作有一半时间内的振动(角)加速度为0,因此振动功率较振动压路机是降低的,这是从"维持钢轮持续振动的功率"角度造成振荡及垂直振动与振动压路机相比节省功率的原因.但这仅仅是一种表象,其实钢轮的振动(角)加速度为0只是2根平行激振轴上激振力的水平分力或垂直分力互相抵消的结果,并不代表不存在负载(单激振轴静偏心矩me或F0为负载)和速度(激振频率f 为旋转速度),而只要有负载和速度就会产生功率消耗,因此振荡压路机及垂直振动压路机较振动压路机节省"维持钢轮持续振动的功率"是一个"伪命题".到底道理何在,他文有述,在此不作展开. 如前所述,振动轴承摩擦功率消耗主要在于阻碍激振轴旋转、发热、滚道磨损及噪声等方面,那种仅仅理解为摩擦发热是十分片面的.但不可否认的是,振动轴承摩擦功率消耗产生的热量是相当可观的,并通过激振室壳体和钢轮幅板等向外释放,有时甚至在30 min内能使激振室内润滑油的温度升高到100 ℃以上(产品标准中原有不超过95 ℃的推荐要求,后来修订时被删除,这也从侧面说明一定的问题),有的甚至高达150 ℃,短期内就会导致润滑油发臭,从而大幅降低润滑效果.如果从直观上粗略估计,对于横跨10~40 t级的振动压路机产品,单激振轴上振动轴承的摩擦功率消耗用于产生热量、磨损即噪声的功率在1~5 kW之间都是合理的. 为了解决振动轴承摩擦发热导致润滑油温升太快、太高的问题,有些产品在左、右2个激振轴之间的联接传动轴上增加了散热风扇,不失为一种"见招拆招"的解决问题之道,但也进一步增加了振动系统的功率消耗. 从式(1)、(2)、(3)中,可以计算激振力F0在振动轴承摩擦功率消耗中所占比重. 基于"负载说"时,表1所列4种产品的振动轴承摩擦功率消耗中,F0所占比重分别为79.8%、74.4%、78.3%和95.0%. 基于"加速度说"时,表1所列4种产品的振动轴承摩擦功率消耗中,F0所占比重分别为99.9%、99.9%、99.9%和100.0%. 由此可见,激振力F0才是引起振动轴承摩擦功率消耗的主要因素,这一结果与实际工况中振动轴承的磨损情况是相符的.尤其是基于"加速度说"时,甚至完全可以用激振力F0代替振动轴承承受的正压力,详见后文计算与分析. 如果将上车质量按"百分之百"的影响进行考虑,即将计算式中的Mgφ用M gφ代替(但不能用M 或M g分别代替M或Mg),则 基于"负载说"时,4个产品的振动轴承正压力P和摩擦功率消耗N摩分别会提高4.0%、3.9%、3.5%和0%. 基于"加速度说"时,4个产品的振动轴承正压力P和摩擦功率消耗N摩分别会提高6.2%、5.8%、5.2%和0%. 由此可见,上车质量对振动轴承摩擦功率消耗的影响有限,表2中的数据并未考虑这一因素的影响. 以上分析都是假设钢轮处于静止状态(即不滚动)的,而压路机在振动或振荡压实时钢轮实际是滚动的.假设压路机压实时的运行速度为3.5 km.h-1,折算成钢轮的滚动速度为0.2 rad.s-1即0.2 Hz. 这里可以分为2种工况,工况一为大振幅时激振轴旋转方向与钢轮滚动方向一致时,振动轴承内、外圈的相对转速会减少0.2 Hz;相反地,工况二为大振幅时激振轴旋转方向与钢轮滚动方向相反时,振动轴承内外圈的相对转速会增加0.2 Hz.需要注意的是,这一相对转速并不影响激振力计算式中的频率值,而仅仅影响摩擦功率计算式中的频率值(实质是振动轴承内圈、外圈的相对转速). 相应地,对应于上述2种工况,各种产品的振动轴承摩擦功率消耗会分别减少0.7%和增加0.7%.这样的差异实际上可以忽略不计,表2中的数据也未考虑这一因素;但重要和需要关注的是激振轴旋转方向与钢轮滚动方向一致时有利于提高铺层表面的压实质量的事实,这也是根据压路机的行驶方向调节振动轴旋转方向即振动轴自动换向控制技术的理论依据. 在式(1)和式(2)中,计算摩擦阻力/力矩时摩擦系数使用附着系数φ代替,而不是滚动阻力系数fr.根据其取值情况来看,对最终计算结果的影响并不十分显著,但经过简单分析即可判断取值的对错. 图5显示了钢轮滚动时在激振力处于水平方向时的受力情况. 按前述思路,可得 式中:Fd为钢轮的附着力;Ff为钢轮的滚动阻力;φ为钢轮的附着系数;fr为钢轮的滚动阻力系数. 很显然,在求取振动轴承正压力的平均值时Fd会加倍,而Ff相抵消,这就是式(1)P=(F0+Mg+2Mgφ)/2π中2Mgφ的由来.因此,不要产生钢轮静止时使用φ、滚动时使用fr的误解. 所谓钢轮悬空振动状态,指的是将车架支撑起来使得钢轮振动时完全离开地面.此时令φ=0,即可直接求得各种振动状态下的振动轴承正压力及摩擦功率消耗;当然也可以详细列式进行计算,由于式中轮系的重力与减振器垂直方向的剪切变形拉力相平衡,因此可以得到相同的结果. 很显然,无论是振动还是振荡及垂直振动产品,此时振动轴承正压力及摩擦功率消耗的计算结果均小于(至少不大于)钢轮在地面上振动时的数值,这一结果能够很好地解释同一台振动压路机在3种状态下测得的振动液压系统压力由大到小排序为:地面振动>弹性材料上振动>轮子悬空振动. 当为了简化分析和计算过程时,上述偏差完全可以忽略.也就是说,可以用激振力F0代替振动轴承的正压力,但不是直接代替,而是间接代替,即振动轴承的正压力是按周期2π呈弦高F0、2个半波的正弦曲线,通过积分可得振动轴承正压力的平均值P=2F0/π. 另一方面,如果考虑振动轴承差异系数1.484的话,则振荡和垂直振动虚拟产品单激振轴的振动轴承摩擦功率消耗正好为振动轮的一半,因为虚拟产品"同口径"的条件就是单激振轴的静偏心矩为振动轮的一半.这不是巧合,而是一种必然. 有一种巧合却真实存在,即"前言"中所述的参考文献[1]中振荡压路机振动轴承的摩擦功率损失计算公式可以转化为N02=16π2μd f3me,与上述简化分析结果"不谋而合";而且从表2中的计算数据也可以得到印证,本文"加速度说"与参考文献[1]的结果相差在1.0%以内.由此可见,参考文献[1]关于振荡压路机振动轴承的摩擦功率损失计算公式是极度简化的结果,也从侧面说明"加速度说"关于振荡压路机振动轴承的摩擦功率损失计算公式是可以采信的. 由此可见,前述所有的分析都是"徒劳"的,只是利用一系列复杂的过程证明了一个简单的结论罢了,而且本文的最终结果就是支持"加速度说"的. 本小节仅仅讨论基于"加速度说"的情形. 表2所列数据均为净功率消耗,并未考虑振动系统的传动效率.与振动压路机的振动系统传动路线相比,振荡及垂直振动产品多出了两组齿形皮带或齿轮传动机构以及中间传动轴,其传动效率约为0.96.只有当计入这一传动效率的影响时,对于进行功率消耗比较的"同口径"才又进了一步. 对于振荡压路机,由于主要用于薄铺层的压实,一般振荡参数匹配(主要指静偏心矩或激振力)较振动压路机偏小约15%(如表1中振荡实际产品),那么在实际产品应用中,振荡压路机振动轴承的摩擦功率消耗为2X3 098/0.96=6 454(W),约为同吨位的振动压路机(10 506 W)的61%.由此可见,从振动轴承摩擦功率消耗大小方面看,振荡压路机较振动压路机是节省振动功率的. 对于垂直振动压路机,由于主要用于厚铺层的压实,一般振动参数(主要指静偏心矩或激振力)匹配较振动压路机偏大约15%.那么在实际产品应用中,垂直振动压路机振动轴承的摩擦功率消耗为2X3 617X1.15/0.96=8 666(W),约为同吨位振动压路机(10 506 W)的83%,约为同吨位振荡压路机(6 454 W)的134%.由此可见,从振动轴承摩擦功率消耗大小方面看,垂直振动压路机较振动压路机是节省振动功率的,但较振荡压路机是耗费振动功率的. 更进一步地,正是由于在实际产品设计中,垂直振动压路机的激振力匹配一般较同吨位的振荡压路机大出约35%左右,即相当于表1中未列出的垂直振动实际产品振动轴承的正压力值将由虚拟产品的61 498 N增加至70 723 N.于是,为了保证振动轴承合理的使用寿命要求,垂直振动实际产品就有可能或有必要使用较同吨位的振荡实际产品大一个规格的振动轴承,如NJ317EC(基本额定动负荷297 kN、平均直径0.132 5 m),则垂直振动实际产品的振动轴承摩擦功率消耗将由虚拟产品的3 623 W增加至3 840 W.这一结果显示,既大于振荡实际产品,也大于振荡虚拟产品,也就是所谓的"此消彼长",因此可以很好地解释垂直振动压路机较振荡压路机耗费振动功率的现实和感知了. 严格来讲,以上所有分析都不是真正意义上的"完全同口径"对比,因为没有尽量兼顾"完全同口径"所要求的3项要素,即钢轮结构型式、振动参数和振动轴承三者均相同,其中"振动轴承相同"分为使用完全相同的振动轴承和使用相同类别且基本额定寿命相同的振动轴承两种情形(由于振动轴承的规格呈阶梯状,不同的产品不可能做到基本额定寿命完全相同,一般取最接近的规格即可,而且兼顾了激振轴的强度要求). 为了更加清晰地对比振动、振荡和垂直振动3种状态下的振动轴承摩擦功率大小,可以振动实际产品为基准(为了兼顾产品现实情况,暂不考虑钢轮结构型式的影响),对其他产品的相关条件进行尽量相同的"极端模拟",并在此基础上按"加速度说"所得到的振动轴承正压力计算其摩擦功率消耗,结果见表4.在表4中,与表1相同的项目全部省略,并按垂直振动压路机产品的设计思路(振动参数比振动实际产品大出约15%)补充了垂直振动"实模"产品. 表4与表1相比,振动轴承配置发生了变化,故统称为"模拟产品"以示区别;其中"虚模"产品表示振动参数与虚拟产品一致,而振动轴承配置是虚拟的,其"同口径"条件(激振力和基本额定寿命相近且同类别的振动轴承,下同)更加严格一些,可以用于理论分析对比;"实模"产品则表示振动参数与实际产品一致,而振动轴承配置是虚拟的,其"同口径"条件严格性稍差,可以用于直觉验证对比. 这里有3点需要说明.其一,表4中关于振动轴承的基本额定寿命计算是基于轴承孔同轴度、润滑油清洁度以及轴承散热等条件处于理想状态下的,实际上现实中很难做到,因此振动轴承的实际使用寿命会比表中所列的要低.振动轴承的损坏主要是由于不同轴导致游隙变小使得负荷急剧增大、杂质混入导致滚道磨损及大量发热、散热不良导致温升异常使得润滑油失效等几个方面原因造成的. 其二,表4中在计算振动轴承的基本额定寿命时使用了F0和P两种方法,而一般情况下以F0方法为准,主要是因为P是一个交变载荷(F0也是一个交变载荷,但是最大值,而P是一个平均值),也未考虑激振轴变形及振动轴承受力不平衡系数γ等不利因素的影响,故P方法必然导致振动轴承基本额定寿命计算值的"虚高",只能仅供参考而已. 其三,表4中振动轴承匹配方案Ⅰ的振荡和垂直振动产品振动轴承基本额定寿命达70 000~200 000 h,说明振动轴承的匹配裕度太大,明显是"大马拉小车",这种"杀鸡用牛刀"的做法必然会增加产品成本,幸好实际产品设计中并没有如此选择振动轴承.振动轴承匹配方案Ⅱ的5种产品振动轴承基本额定寿命在9 000~13 000 h之间,基本上可以说是"恰到好处"的. 以上分析过程十分复杂,然而通过对比表2和表4可以发现,其实结论异常简单. (1)表2中,振荡和垂直振动实际产品的振动轴承摩擦功率消耗较振动实际产品分别降低41.0%和23.4%(参考表4中的振动参数),而振荡和垂直振动虚拟产品的振动轴承摩擦功率消耗较振动实际产品分别降低30.1%和31.1%.30.1%和31.1%是进行理论分析对比时需要关注的数值,虽然为未考虑振动轴承差异的情形,但符合产品实际情况,因此具有一定的实践意义. (2)表4中,当使用相同的振动轴承时,振荡和垂直振动实模产品的振动轴承摩擦功率消耗较振动实际产品分别降低12.5%和增高13.6%;振荡和垂直振动虚模产品的振动轴承摩擦功率消耗较振动实际产品分别增高3.7%和2.2%.这一组数据较上列数据明显降低,说明振动轴承摩擦功率的消耗与振动轴承的参数(涉及平均直径和摩擦系数)密切相关. (3)表4中,当使用相同类别且基本额定寿命相近的振动轴承时,振荡和垂直振动实模产品的振动轴承摩擦功率消耗较振动实际产品分别降低43.0%和15.2%;振荡和垂直振动虚模产品的振动轴承摩擦功率消耗较振动实际产品分别降低27.6%和28.6%.27.6%和28.6%是进行理论分析对比时需要关注的数值,而且是振动轴承为相同类别且基本额定寿命相近的情形,既符合产品基本实际情况,也为产品优化指明了方向,因此更加具有理论和实践意义. (4)相对于振动压路机,振荡和垂直振动产品之所以节省整个振动系统的功率,主要是由于振动轴承摩擦功率消耗的节省(暂时结论,他文有述);而振动轴承摩擦功率消耗的节省,究其根源主要在于可以使用和实际使用了较小规格的振动轴承(表1);而且可以使用较目前再小2~3个规格的振动轴承(表4),则其振动轴承的摩擦功率消耗还有降低的空间,同时可以降低产品成本,即表4中振动轴承匹配方案Ⅱ才是最佳方案(不考虑产品通用化方面的要求时). 在实际工作中,振动压路机的振动功率是在不断变化的.造成振动功率变化的原因除与被压实土壤的物理特性有关以外,还与振动压路机本身的工作状态有关,如发动机油门所处位置(涉及振动频率,随着发动机转速增加一般振动频率会同比增加,振动功率也会同比增加)、振动轴承的润滑条件(涉及振动轴承的摩擦阻力矩及摩擦发热功率消耗)以及振动轴承的支承条件. 振动轴承的支承条件,包括振动轴刚度、轴承极限转速和轴孔同轴度等因素,其中轴孔同轴度包含振动轴及轴承孔的同轴度、振动轴承径向游隙以及轴承与轴或孔的配合3个方面,决定了实际运转过程中振动轴承的运动游隙,这对振动功率的消耗影响尤其显著;如果实际运动游隙过小,由于轴承发热将导致滚动阻力加大,使得振动功率消耗急剧上升(既包括振动轴承摩擦发热,也包括摩擦阻力矩使得振动轴旋转功率消耗增加).因此,在设计振动轮时,振动轴及轴承孔一般都有较高的同轴度要求(有些产品直接使用调心轴承也是出于同样的目的),振动轴承一般选取C4甚至C5的游隙,而且振动轴承与轴及轴承孔采取较松一些的配合. 振动轴承的摩擦功率损失不仅转化成了大量热量,而且也造成轴承滚道磨损,进而使得润滑油污染;而滚道磨损又会进一步急剧增加发热量,以及增大轴承运转噪声,最终导致振动轴承烧毁.这是振动轴承最主要的失效模式. 对于普通的两振幅振动压路机,拆解使用过一段时间的振动轴承,可以发现始终是内圈外滚道上与固定偏心块同侧部位的1/4左右圆弧磨损,尤以正中部位磨损最为严重,而其它部位几乎没有磨损痕迹.这一现象并不超出我们的想象,主要是由于轴承内圈与轴颈为过盈配合,使得固定偏心块同侧部位(即合静偏心矩同侧,也即激振力方向同侧)的轴承内圈外滚道始终受力.换而言之,振动轴承正压力P的方向始终与激振力F0的方向一致,这也是与前文中的受力分析的结果一致的. 图6显示了传统结构的振动轴上振动轴承的磨损情况,大振幅状态下将产生重度磨损,小振幅状态下将产生轻度磨损;两相叠加,不可避免地产生严重磨损,从而大大缩小振动轴承的使用寿命. 图7显示了一种改进结构的振动轴上振动轴承的磨损情况,大振幅状态下将产生重度磨损,小振幅状态下将产生轻度磨损;但两者不是叠加,而是磨损面处于相对位置,从而可以有效延长振动轴承的使用寿命,这也是振动轴承的摩擦功率消耗与静偏心距大小密切相关最有力的证据. 为了显示两种结构振动轴的区别,图6、7中特意用焊缝的形式明确了固定偏心块.对于图7所示结构,也可以是中间为固定偏心块(小偏心矩),而两侧为活动偏心块(大偏心矩). (1)振动参数的"同口径"是进行不同产品振动轴承摩擦功率消耗对比的前提,包括振动频率相同,保持参振质量不变,振荡和垂直振动压机单轴上的最大和最小静偏心矩均为振动压路机的一半;同时,钢轮的半径、平行双轴之间的距离等具体结构尺寸也必须相同,而钢轮的其他结构尺寸以及主要质量分布(涉及轮子的转动惯量)等,也必须尽量相同. (2)从振动、振荡和垂直振动产品的振动轴承摩擦功率消耗数值计算结果来看,本文提出的"负载说"是不可采信的;而参考文献[1]的理论基础也是基于"负载说",其计算结果不可采信便是情理之中的事情,而且振动实际产品的振动轴承正压力之和仅为19 985 N(4个振动轴承),明显小得太过离谱(激振力为197 840 N),导致4种产品的振动轴承摩擦功率消耗在相对值的大小上存在"方向性"错误. (3)从单激振轴上所有振动轴承正压力之和方面考虑,4种产品与其各自的负载(静偏心矩或激振力)的比值相当接近,并且实践证明也与各自的振动轴承规格匹配及实际使用寿命相适应,说明基于"加速度说"的振动轴承正压力计算方法不存在原则性问题.并且鉴于加速度计算值符合实际情况的事实,加上在考虑振动轴承差异系数后的单激振轴摩擦功率消耗的"相对值"的合理性,说明"加速度说"是基本可以采信的. (4)激振轴上所有振动轴承的正压力之和P与该激振轴的激振力F0的关系.基于本文"加速度说"时,P≈(0.60~0.63)F0,适用于振动、振荡和垂直振动3种振动型式.而参考文献[1]的计算结果显示,振动时P≈(0.08~0.10)F0,振荡时P≈(0.60~0.63)F0,垂直振动时P≈(0.08~0.10)F0;而且这种关系不仅可以扩展到其它吨位的单钢轮振动压路机上,也同样适用于双钢轮振动压路机.因此,参考文献[1]明显从"源头"上存在"厚此薄彼"的嫌疑,必然造成后续振动轴承摩擦功率计算结果的"云泥之别". (5)振动轴承摩擦功率的消耗,除阻碍激振轴旋转以外,还以发热、滚道磨损及噪声的方式表现出来,而且三者是互相影响的;磨损杂质和温度升高的后果使得润滑条件恶化,从而极大地影响振动轴承的使用寿命.如果从直观上粗略估计,1/10左右的摩擦功率消耗在振动轴承的发热、滚道磨损及噪音方面是比较合理的;对于横跨10~40 t级的振动压路机产品,单激振轴上振动轴承的摩擦功率消耗用于产生热量、磨损和噪声的功率在1~5 kW之间都是比较恰当的估计. 振动轴承的损坏主要是由于不同轴导致游隙变小使得负荷急剧增大、杂质混入导致滚道磨损及大量发热、散热不良导致温升异常使得润滑油失效等几个方面原因造成的,最终导致轴承烧毁.除了设计和制造过程中保证轴承孔及激振轴轴颈的同轴度以外,为了改善振动轴承的润滑条件,一般在激振室内安装有强磁铁以吸附润滑油中的因磨损而脱落的金属杂质;有些产品在左、右2个激振轴中间的传动轴上,增加了散热风扇以控制润滑油温不致升得太快、太高,不失为一种"见招拆招"的解决问题之道,但也进一步增加了振动系统的功率消耗. (6)基于"加速度说"时,4种产品的振动轴承摩擦功率消耗中,F0所占比重均在99.9%以上,可见激振力F0才是引起振动轴承摩擦功率消耗的主要因素,这一结果与实际工况中振动轴承的磨损情况是相符的.为了简化分析和计算过程,甚至可以用激振力F0代替振动轴承承受的正压力,但不是直接代替,而是间接代替,即振动轴承的正压力是按周期2π呈弦高F0、2个半波的正弦曲线,通过积分可得振动轴承正压力的平均值P=2F0/π. (8)假设压路机压实时的运行速度为3.5 km.h-1,折算成钢轮的滚动速度为0.2 Hz,即振动轴承的内圈相对于外圈转速增加或降低0.2 Hz,这对振动轴承摩擦功率消耗的影响约0.7%,完全可以忽略不计,但不能无视激振轴旋转方向与钢轮滚动方向一致时有利于提高铺层表面的压实质量的事实,这也是根据压路机的行驶方向调节振动轴旋转方向即振动轴自动换向控制技术的理论依据. (9)在计算钢轮与地面的摩擦阻力或阻力矩时,其摩擦系数可以用附着系数φ代替,但不能用滚动阻力系数fr代替;也不存在钢轮静止时使用φ代替、钢轮滚动时使用fr代替的情形. (10)从轴系角度出发,静偏心矩和振动轴承摩擦阻力是负载;而无论是振动、振荡还是垂直振动型式,激振轴都在以相同的频率旋转,振动轴承的受力方式也是一样的,故振动系统消耗的功率只与激振轴的负载相关.因为振荡及垂直振动单激振轴上的静偏心矩只有振动的一半,因此可以使用较小规格的振动轴承,这是从振动轴承"摩擦功率"角度造成振荡及垂直振动较振动压路机节省功率的原因. 从轮系角度出发,参振质量和钢轮与地面的附着系数产生的摩擦阻力是负载,而振动轴承的摩擦阻力属于内力;那种将振荡及垂直振动压路机的钢轮简单地看作有一半时间内的振动(角)加速度为0,因而较振动压路机可以节省"维持钢轮持续振动的功率"的说法仅仅是一种表象,其实钢轮的振动(角)加速度为0只是2根平行激振轴上激振力的水平分力或垂直分力互相抵消的结果,并不代表不存在负载(单激振轴静偏心矩me或F0为负载)和速度(激振频率f为旋转速度),而只要有负载和速度就会产生功率消耗,因此振荡压路机及垂直振动压路机较振动压路机节省"维持钢轮持续振动的功率"是一个"伪命题". (11)从现实产品来看,振荡和垂直振动实际产品的振动轴承摩擦功率消耗较振动实际产品分别降低41.0%和23.4%;而从虚拟产品来看,较振动实际产品分别降低30.1%和31.1%.后者是进行理论分析对比时需要关注的数值,虽然未考虑振动轴承差异的情形,但符合产品实际情况,因此具有一定的实践意义. 与振动压路机相比,振荡和垂直振动压路机振动轴承摩擦功率消耗的节省,究其根源主要在于可以使用和实际使用了较小规格的振动轴承,而且可以使用较目前再小2~3个规格的振动轴承,则其振动轴承的摩擦功率消耗还有降低的空间,同时可以降低产品成本,即表4中振动轴承匹配方案Ⅱ才是最佳方案,兼顾了激振轴的强度要求,但没有考虑产品通用化方面的要求. 当使用相同类别且基本额定寿命相近的振动轴承时,振荡和垂直振动实模产品的振动轴承摩擦功率消耗较振动实际产品分别降低43.0%和15.2%;振荡和垂直振动虚模产品的振动轴承摩擦功率消耗较振动实际产品分别降低27.6%和28.6%.后者是进行理论分析对比时需要关注的数值,而且是振动轴承为相同类别且基本额定寿命相近的情形,既符合产品基本实际情况,也为产品优化指明了方向,因此更加具有理论和实践意义. 综上,关于实际产品中,振荡和垂直振动压路机较振动压路机节省"振动功率"的最终结论,只需记住"一个原因"和"两个数字"."一个原因"即由于实际使用了较小规格的振动轴承的缘故,从而节省振动轴承摩擦功率的结果;"两个数字"即对仅振动参数严格"同口径"的产品而言节省约30%,对振动参数和振动轴承均严格"同口径"的产品而言节省约28%. (12)通过拆解激振轴上的振动轴承可以发现,磨损部位始终是内圈外滚道与静偏心距同侧部位的1/4左右左右圆弧,而其他部位几乎没有磨损痕迹.对于传统结构振动轴上的振动轴承,由于大振幅状态下的重度磨损,与小振幅状态下的轻度磨损相叠加,不可避免地产生严重磨损,从而大大缩小振动轴承的使用寿命.而一种改进结构,可以使大振幅与小振幅状态下的磨损面处于相对位置,从而可以有效延长振动轴承的使用寿命,这也是振动轴承的摩擦功率消耗与静偏心距大小密切相关最有力的证据. (13)用一台平行双轴结构钢轮的垂直振动压路机,重新匹配偏心块的初始相位差和旋转方向,即可得到振动或振荡压路机,这样就保持了振动参数和振动轴承的一致性,这是一次性解决对比"同口径"3个问题的"终极"方法.在此情况下,振动状态的振动轴承正压力在原来的基础上稍有降低,而且由于振动轴承差异系数1.484的积极影响,将导致振动轴承摩擦功率消耗大幅降低;那么,节省振动功率到底"鹿死谁手"就不一定了,振动压路机实现"反转"也不是不可能的.而且这才是从理论上分析和对比圆周振动、振荡和垂直振动哪种振动型式(不是指实际产品,也不是指相同压实效果为前提的对比情形)节省振动功率最精确的方法,其他都是结合实际产品情况的近似方法.
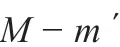

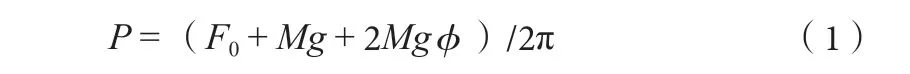



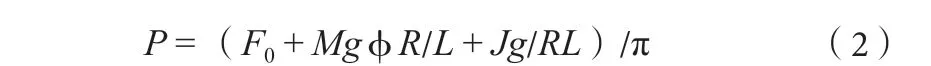




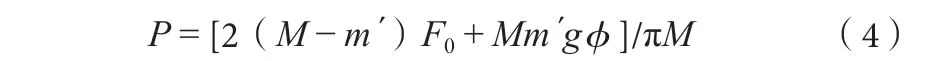
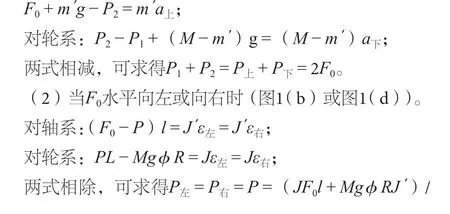
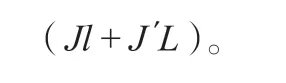



2 振动轴承摩擦功率计算


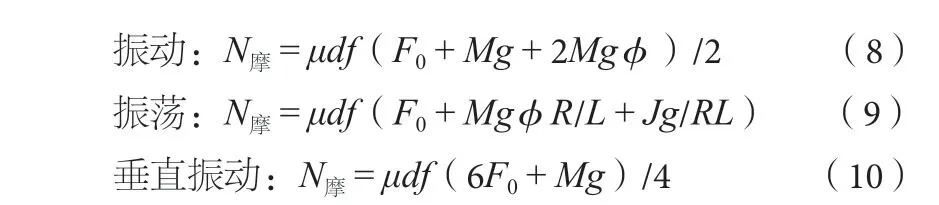

3 计算结果分析与讨论
3.1 基于"负载说"的计算结果分析
3.2 基于"加速度说"的摩擦功率数值分析

3.3 振动轴承摩擦发热量评估
3.4 激振力与重力的比重
4 其他因素延伸分析与讨论
4.1 上车质量的影响
4.2 钢轮滚动速度的影响
4.3 滚动阻力系数与附着系数的区别

4.4 钢轮悬空状态的振动轴承摩擦功率消耗


4.5 实际产品的振动轴承摩擦功率消耗对比
4.6 极端条件下振动轴承摩擦功率消耗模拟对比

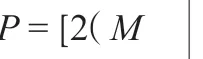
4.7 振动轴承磨损情况及激振轴改进设计


5 结语

