钢渣沥青混合料碾压温度场

2019-04-15武建民杨永利吴春生

筑路机械与施工机械化 2019年3期

周雄，武建民，杨永利，3，吴春生

(1.陕西路桥集团有限公司，陕西西安 710075； 2.长安大学教育部特殊地区公路工程重点实验室，陕西西安 710064； 3.中公高科养护科技股份有限公司，北京 100095)

0 引言

温度是沥青混合料施工时最敏感的条件，要达到要求的高压实度和低空隙率，压实机械必须在满足要求的温度条件下完成压实工作。如果沥青混合料温度下降比较快或温度较低，即使加大压实功，也难以达到要求的压实度。在沥青混合料压实方面，国内外学者进行了大量的研究。Mahboub K C等通过对沥青混合料冷却规律的研究，提出了有效压实时间的预估方法，以便于在施工中对混合料温度进行控制[1]。Jordan 和 Thomas研究了摊铺后热拌沥青混合料的降温规律，认为沥青混合料温度在刚摊铺时下降迅速，主要是由于基层温度较低的原因，随后的温度下降速率主要取决于沥青层摊铺厚度、摊铺温度等。李辉等研究表明：碾压时表面层下5 cm范围内温度提高有限，5～8 cm以下深度处温度基本保持不变[2]。石鑫等研究认为，沥青混合料温度下降至 85 ℃～90 ℃之前是有效压实时间[3]。杨春霞的研究认为，SMA-13沥青混合料自摊铺开始至内部降温到100 ℃左右为有效压实时间[4]。

近些年，钢渣沥青混合料以其优良的路用性能日益得到重视[5-6]，已有的研究大多针对钢渣沥青混合料的材料组成及路用性能[7-9]，而钢渣沥青混合料中含有一定数量的钢渣作为骨料，钢渣的铁成分含量相对较高，是良好的热传导介质，这使得钢渣沥青混合料相对于传统沥青混合料导热性能更好。因此，如何控制好钢渣沥青混合料的有效压实时间是施工的关键。本文依据路面温度场热传导理论和钢渣沥青混合料的热物性参数，使用有限元软件进行钢渣沥青混合料碾压温度场数值分析，为钢渣沥青混合料施工提供参考。

1 路面结构与碾压温度场分析模型

1.1 碾压温度场分析建模

沥青路面碾压温度场模型的基本假设为：路面结构各层材料具有各向同性且均匀连续；路面结构各层层间温度传递和热流交换连续；路面结构的温度梯度只沿厚度方向变化，温度梯度沿道路横截面方向为零；对于半无限空间体，在足够深处温度场基本恒定。

表1为陕西省代表性高速公路沥青路面结构，采用的模型尺寸为：路面宽度6 m，土基深度6 m。选择上面层钢渣SMA-13为研究层。

表1 代表性沥青路面结构

采用的单元类型为二次热传导单元(DC2D8)。X方向网格尺寸均为0.1 m；Y方向沥青上面层网格尺寸为0.005 m，中、下面层网格尺寸为0.01 m，基层网格尺寸为0.02 m，土基网格尺寸为0.1 m。

1.2 温度场边界条件

对于路面结构，假设水平方向的温度梯度为零，则侧面的边界条件不予考虑，路面的上表面为主要边界，底部无限深处为次要边界。

1.2.1 表面边界条件

沥青混合料在摊铺碾压时，上表面为路面热传导的主要边界，Tan S等[10]研究表明，路表与外界环境主要通过3种方式进行着热交换，即太阳辐射Hr、空气对流换热Hc和空气辐射换热He。

Ho=-Ha+Hc+He

(1)

式中：Ho为进入空气的热流密度；Ha为路表吸收的太阳辐射强度；Hc为空气与路表的对流换热；He为空气和路表的辐射换热。

假设单位面积上太阳单位时间辐射的热量为I0(W·m-2)，则路表面吸收的热量Ha可表示为

Ha=αs·I0

(2)

式中：αs为路表面对太阳辐射的吸收率。

太阳辐射以热流密度的形式施加于路表面，沥青面层对太阳辐射的吸收率取0.90。

除了太阳辐射传递热量外，路表面还与大气发生热量对流换热。

Hc=hc(Ts-Ta)

(3)

式中：hc为空气对路面的对流换热系数(W·m-2·℃)，与风速有关；Ta为大气温度(℃)；Ts为路表面的温度(℃)。

空气对流换热主要与风速有关，路表面与空气的热交换系数hc与风速vw呈线性关系。

hc=3.7vw+9.4

(4)

式中：hc为热交换系数(W·m-2·℃-1)；vw为日平均风速(m·s-1)。

建立路表面有效辐射的边界条件，即

He=εσ[(Ts-TZ)4-(Ta-TZ)4]

(5)

式中：ε为路表面反射率(黑度)，沥青路面取0.81；σ为Stefan-Boltzmann常数，σ=5.669 7×10-8W·(m2·K4)-1；TZ为绝对零度值(℃)，TZ=-273 ℃。

1.2.2 层间连续条件及底部边界条件

设路面各结构层之间的接触良好，在层间界面，上下两层的温度及热流是完全连续的。

结构层底部施加20 ℃恒温边界条件。假定中面层表面温度与大气温度相同，先对中面层及以下结构进行稳态分析，在稳态温度场的基础上再对整个路面结构进行瞬态温度场分析。

1.3 温度场数值分析时的热物理性质参数

路面结构最主要的2个热物理参数为导热系数和比热容。热拌沥青混合料碾压过程中由摊铺后的松铺状态碾压形成密实状态，其空隙率也随之发生变化。比热容与沥青混合料的空隙率无关，只取决于沥青混合料各组分的比热容和质量百分率[11-13]。因此，在沥青混合料碾压过程中，其比热容变化不大，可视为常数。而沥青混合料的导热系数与混合料各组分的导热系数、各组分体积百分率以及空隙率等有关[14-18]。Williamson推导出了如下的沥青混合料导热系数公式。

(6)

式中：k为沥青混合料的导热系数；ka为矿料的导热系数；kb为沥青的导热系数；kv为空气的导热系数；kw为水的导热系数；m、n、p、q分别为沥青混合料中矿料、沥青、空气和水的体积百分率。

其中，沥青的导热系数取0.699 W·(m·℃)-1，空气的导热系数取0.024 W·(m·℃)-1，水的导热系数取0.54 W·(m·℃)-1，水的体积百分率取0。

测定出不同钢渣体积掺量下的SMA-13混合料密实状态下的导热系数k，见表2。对于松铺状态下的导热系数k′(松铺系数取为1.2，即p=0.2)，需根据式(6)进行推导：先计算出不同钢渣体积掺量的SMA-13混合料密实状态下各组分的体积百分率m、n、p；然后取kb= 0.699 W·(m·℃)-1，kv=0.024 W·(m·℃)-1，代入式(6)求出不同钢渣体积掺量下合成矿料的导热系数ka，见表2；最后依据松铺状态下各组分的体积百分率m′、n′、p′及上一步求取的ka、kb、kv重新代入(6)求出不同钢渣体积掺量的SMA-13混合料松铺状态下的导热系数k′，见表3。

文献[19]试验测得玄武岩的导热系数为1.7 W·(m·℃)-1，石灰岩的导热系数为2.5 W·(m·℃)-1。由表3得出普通SMA-13混合料的合成矿料导热系数为1.867 W·(m·℃)-1，由此验证了密实状态下沥青混合料导热系数测定的准确性。随着钢渣的体积掺量增加，合成矿料导热系数也随之增加。由表3可知，SMA-13混合料松铺时的导热系数小于压实时的导热系数；因此，钢渣沥青混合料在松铺状态下放热较密实状态放热慢，相应地在松铺状态下有效压实时间最长，在密实状态下有效压实时间最短。在混合料在碾压过程中，这2个状态为极限状态，故实际有效压实时间应介于这2个时间之间。

表2 不同钢渣体积掺量下合成矿料导热系数

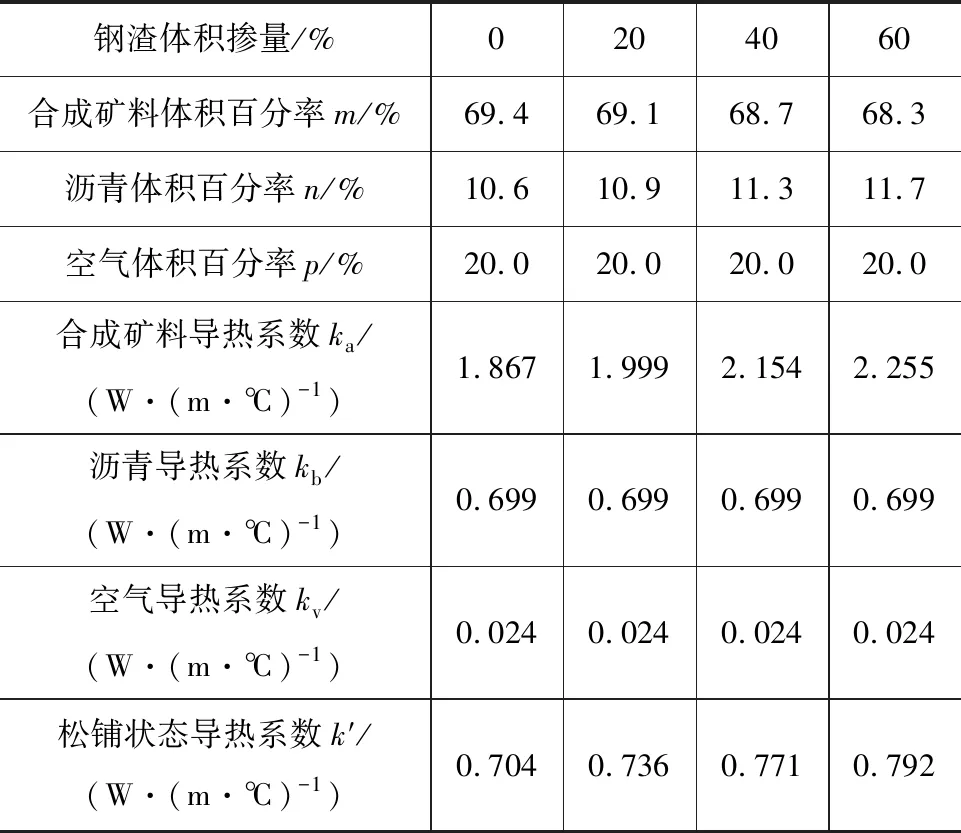
表3 不同钢渣体积掺量SMA-13混合料松铺状态下的导热系数

钢渣SMA-13混合料选取钢渣体积掺量40%的热物性参数建立碾压温度场，并与普通SMA-13混合料进行对比，见表4。

仿真分析中假定底层材料导热系数和比热保持不变，这也是目前所有铺筑热扩散仿真研究中采用的基本假定。参照张秀华等[20]的研究成果，设定中面层及其以下层次材料热物性参数，见表5。

表4 上面层材料的热物理性质参数

表5 中面层及以下层次材料的热物理性质参数

2 钢渣沥青混合料碾压温度场数值分析结果

2.1 当量温度换算

由于摊铺层不同深度处沥青混合料的温度变化较大，故不宜采用某一深度处的温度代表摊铺层的整体温度。研究中根据温度和黏度的对应关系，先求出混合料摊铺层各点某时刻温度所对应的沥青黏度，得到平均黏度值，再通过黏-温关系，反算出平均黏度所对应的温度值，称之为当量温度。国际上通用的沥青黏度与温度关系的公式是Saal公式。

lglg(η×103)=a-blg(273+T)

(7)

式中：η为黏度；T为温度。

表6 SBS改性沥青黏度测试结果

根据表6测试结果得到拟合方程为

lg·lg(η×103)=7.877-2.825lg(273+T)

(8)

由式(8)便可以实现沥青黏度和温度的互算。

2.2 有效压实时间

有效压实时间是指混合料从运输至现场的温度降至最低允许碾压温度所需的时间。对于SMA-13混合料，自摊铺至内部降温到100 ℃左右时为有效压实时间。本文以此温度为有效压实的标准，利用碾压温度场模型模拟钢渣SMA-13混合料的有效压实时间，并与普通SMA-13混合料作对比。

2.3 碾压温度场数值分析

以气候条件较差的陕北地区为例，上面层SMA-13混合料摊铺温度取160 ℃，路面结构中下面层初始温度取为20 ℃，结构层底部施加20 ℃恒温边界条件，铺层厚度为4 cm，环境温度取25 ℃，风速为3 m·s-1，太阳辐射强度取500 W·m-2。

针对钢渣体积掺量40%的SMA混合料和普通SMA混合料建立碾压温度场进行数值分析，计算得出铺层当量温度随时间变化的规律，如图1所示。

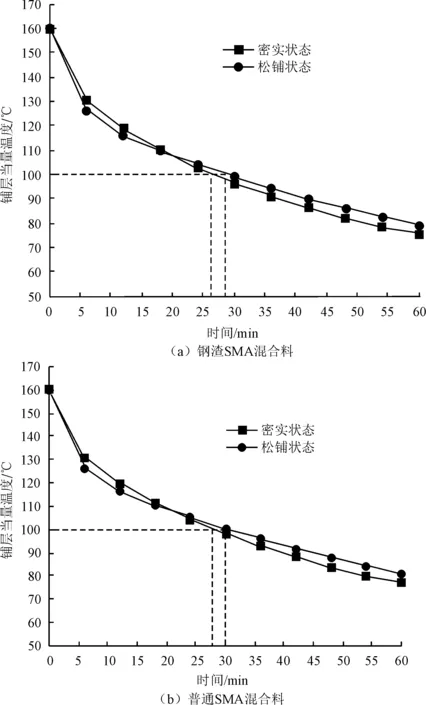
图1 两种SMA混合料不同碾压状态下铺层当量温度随时间的变化

由图1可以得出以下几点。

(1)无论松铺状态还是密实状态，铺层当量温度均随着时间的延长而降低；并且在摊铺初期当量温度下降速率明显大于后期的下降速率。这是由于，刚开始摊铺的热拌沥青混合料与温度较低的中面层会产生热流交换，随后热交换速率逐渐变缓。

(2)在20 min内，松铺状态下的SMA混合料当量温度下降速率大于密实SMA混合料的下降速率；在20 min后，松铺状态下的SMA混合料当量温度下降速率放缓且小于密实SMA混合料的下降速率。这主要是因为，碾压初期热量松铺状态下的SMA混合料不仅向铺层表面和中面层传递热量，而且因其空隙率大存在混合料内部热量损失。后期松铺状态下的SMA混合料导热系数较密实SMA混合料小，热量损失也相应减少。

(3)无论松铺状态还是密实状态，在60 min内，钢渣SMA混合料较普通SMA混合料当量温度下降快1 ℃～2 ℃，说明掺有钢渣的SMA混合料热量损失较普通SMA混合料多，但对施工温度控制影响不大。

(4)钢渣SMA混合料有效压实时间介于26.2～28.6 min，普通SMA混合料有效压实时间介于27.8～30.0 min。钢渣沥青混合料热量损失较普通沥青混合料略快。在文中给定的工况下，2种SMA混合料的有效压实时间仅为30 min左右。