关于半对偶双模的强FP-内射模和强FP-投射模*
2019-04-13何东林李煜彦
何东林,李煜彦
(陇南师范高等专科学校 数信学院,甘肃 陇南742500)
0 引言
半对偶模是环模理论和同调代数中的重要模类.许多作者先后对其进行了研究,并得到了很好的结论.[1-5]特别地,Holm和White[4]将半对偶模的概念推广到任意一对结合环R和S上,他们利用这个概念研究了关于半对偶模的Auslander类和Bass类,而Auslander类和Bass类在Gorenstein同调理论中扮演着重要的角色.2011年Zhang和Ouyang引入了关于半对偶模C的FP-内射模,即C-FP-内射模.在此基础上,Hu[7]利用C-FP-内射模研究了弱Auslander类和Bass类.2017年Li等[8]介绍了强FP-内射模,它是FP-内射模的一个推广.
自然而然地,可考虑关于半对偶模C的强FP-内射模和强FP-投射模.
文中的环R和S均指有单位元的结合环,模指酉模.用RM(MR)表示左(右)R-模M,SMR表示左S-右R双模M.如果对任意有限表示模RN,都有Ext1R(N,M)=0,那么称RM是FP-内射模.[9]如果对任意FP-内射模RM,都有Ext1R(Q,M)=0,那么称RQ是FP-投射模.[9]用f I(R)和f P(R)分别表示所有FP-内射左R-模和FP-投射左R-模组成的子范畴.如果对任意有限表示模RN,都有ExtiR≥1(N,M)=0,那么称RM是强FP-内射模.[8]用sfI(R)表示所有强FP-内射左R-模组成的子范畴.
设x是左R-模范畴的一个子范畴.记⊥1x={RM|对任意X∈x有Ext1R(M,X)=0},⊥x={RM|对任意X∈x有ExtiR≥1(M,X)=0}.对偶地,可定义x⊥1和x⊥.设SCR是一个双模.如果满足以下条件:(1)SC具有有限生成投射左S-模分解;(2)CR具有有限生成投射右R-模分解;(3)S≅End(CR)且R≅End(SC);(4)ExtiR≥1(C,C)=0且ExtiS≥1(C,C)=0,则称SCR是一个半对偶双模.进而,如果对任意模SN和MR都有:若 HomS(C,N),则N=0;若,则HomR(C,M)=0,则M=0称半对偶模SCR是忠实的.称同时满足条件(a1)(C,M)=0;为同构的模RM组成的类为关于半对偶模SCR的Auslander类,记为AC(R).称同时满 足 条 件 (b1)ExtiS≥1(C,N)=0;(b2)ToriR≥1(C,HomS(C,N))=0;(b3) 自 然 同 态 vN:C ⊗RHomS(C,N)→N为同构的模SN组成的类为关于半对偶模SCR的Bass类,记为BC(S).下文中的模C均指半对偶双模SCR.其余未涉及的概念和记号参见文献[7]和[10].
1 定义和引理
定义1 设M和N是左R-模.如果存在强FP-内射模SE,使得RM≅RHomS(C,E),那么称模M是强C-FP-内射模.用sfIC(R)表示所有强C-FP-内射左R-模组成的子范畴.进而,如果对任意M∈sfIC(R),都有ExtiR≥1(N,M)=0,那么称模N是强C-FP-投射模.用sfPC(R)表示所有强C-FP-投射左R-模组成的子范畴.

E∈⊥1sfI(S)∩sfI(S)}.
引理1[6]设SM是FP-内射模,则M∈BC(S).
引理2[4]设M和M'是左R-模,N和N'是左S-模,则(
1)如果M∈AC(R)且ToriR≥1(C,M')=0,那么
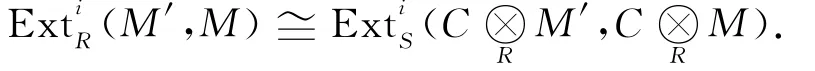
(2)如果N∈BC(S)且ExtiS≥1(C,N')=0,那么
ExtiS(N,N')=ExtiR(HomS(C,N),HomS(C,N')).
2 主要结论
定理1 设SCR为半对偶双模,则
(1)模RU∈sfIC(R)当且仅当模RU∈AC(R)且C⊗RU是强FP-内射左S-模.
(2)模US∈sfIC(S)当且仅当模US∈AC(S)且U⊗RC是强FP-内射右R-模.
证明:(1)先证充分性.设模RU∈sfIC(R),则存在sE∈sf i(S),使得U≅HomS(C,E).由引理1知E∈BC(S).从而有同构

必要性显然成立.
(2)证明过程与(1)类似.
定理2 设SCR为半对偶双模且M是左R-模,则以下条件等价:
(1)RM强C-FP-投射模;
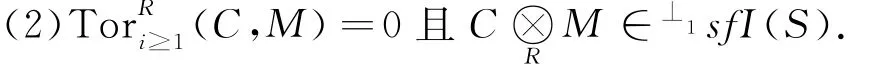
证明:(1)⇒(2)设RM强C-FP-投射模.令SN是一个忠实内射S-模,则HomS(C,N)是强C-FP-投射模.从而有ExtiR≥1(M,HomS(C,N))=0.因为对任意i>1有同构

根据定理1可得HomS(C,U)∈AC(R).因此有同构
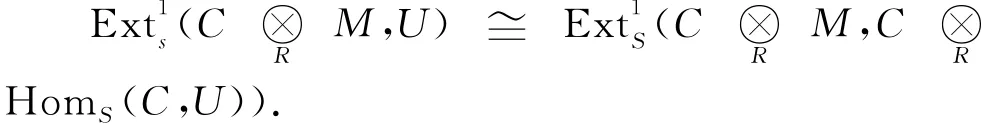
又由引理2及HomS(C,U)∈sfIC(R)知.

N∈AC(R)且C⊗RN是强FP-内射S-模.根据引理2可知,对任意i≥1有
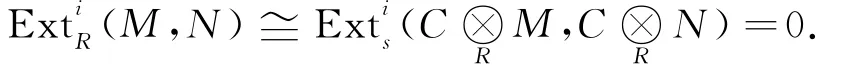
因此RM是强C-FP-投射模.
定理3 设SCR为半对偶双模且M是左R-模,则以下条件等价:

又因为模M∈sfPC(R)且HomS(C,E)∈sfIC(R),所以Ext1RHomS(C,N))=0.从而有Exts1(E,N)=0.由N的任意性可知E∈⊥1sfI(S).因此M ∈sfICFP(R).
由定理3易得如下推论.
推论1 设RM∈sfICFP(R)且N∈sfIC(R),则对任意i≥1,都有

