基于数学史的高考数学试题的赏析与思考

2019-04-13广东省东莞市万江中学523057袁建钊

中学数学研究(广东) 2019年6期

广东省东莞市万江中学(523057) 袁建钊

广东省东莞市第七高级中学(523500) 谭文艳

1、引言

在我国, 早在2003年颁布的《普通高中数学课程标准(实验)》,明确指出要体现数学史的文化价值,强调“数学课程应适当反映数学的历史、应用和发展趋势”[1].2016年颁布的《关于2017年普通高考考试大纲修订内容的通知》首次非常正式地明确要求要把数学文化渗透入数学试题.2017年颁布的《普通高中数学课程标准(2017年版)》中谈到,数学文化融入课程内容,数学文化融入整个课程的结构里面[2].随着课程改革的不断深入,数学的人文价值更明显地凸显出来,已普遍受到重视.

纵观最近几年的全国各地的高考,出现了一些以数学史为载体的高考试题,成为新课改理念下高考改革和发展的一道靓丽风景.尤其是全国卷,已经连续多年命制此类考题,逐渐形成了高考数学卷的一大特色和亮点.如2018年全国卷3 第3 题以优秀的中华木土文化为背景, 以榫卯为载体, 从更高的要求和不同的角度,考查考生的空间想象能力和空间图形的转化能力;理科数学全国卷1 第10 题以古希腊数学家希波克拉底在研究化圆为方问题时曾研究过的图形为背景,设计了一个几何概型问题,引导考生热爱数学文化,关注几何之美.这一方面是为师生在平时学习时关注数学史提供“导向”,另一方面数学史作为一种数学文化走进高考,让高考试卷平添了几分文化色彩与气息.

2、试题检索

笔者查阅了近年来全国卷的高考数学试卷后发现: 几乎每年都会出现与数学史相关的试题,涉及数学史内容极为丰富, 如古希腊数学家希波克拉底的几何图形、“哥德巴赫猜想”、“秦九韶算法”、“太极图”、《算法统宗》等(见表1),它们融知识、方法、思想、能力、素质于一体,背景新颖,内涵深刻, 富有新意, 使数学的文化性、应用性与理论性有机结合,相互渗透,有目的地来考查考生的学习潜能和数学素养.

表1 近年来全国卷中基于数学史的高考试题

3、试题赏析

现遴选几道基于数学史的高考试题供广大师生赏析:

例1(2018 全国卷1 理10)下图(图1)来自古希腊数学家希波克拉底所研究的几何图形,此图由三个半圆构成,三个半圆的直径分别为直角三角形ABC 的斜边BC,直角边AB,AC,△ABC 的三边所围成的区域记为I,黑色部分记为II,其余部分记为III,在整个图形中随机取一点,此点取自I,II,III 的概率分别记为p1,p2,p3,则( )

A.p1=p2B.p1=p3C.p2=p3D.p1=p2+p3

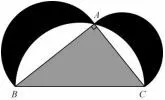
图1

赏析此题以古希腊数学家希波克拉底在研究化圆为方问题时曾研究过的图形为背景, 设计了一个几何概型问题,引导考生热爱数学文化,关注几何之美.面积大小是关键,翻开初中八年级上数学课本我们发现, 原来源头在勾股定理,以直角三角形三边分别往外作正方形,大正方形的面积等于两小正方面积之和.此题同样如此,大的半圆面积等于两个小半圆面积之和,可知两区域面积相同.学生要解答必须有一点数学素养,在高中学习阶段,这样的几何题很少涉及,很多同学早就把勾股定理忘记了,进一步凸显在教学中渗透数学史的意义.

例2(2018 全国卷3 文3 理3)中国古建筑借助榫卯将木构件连接起来,构件的凸出部分叫棒头,凹进部分叫卯眼,图中木构件右边的小长方体是棒头.若如图摆放的木构件与某一带卯眼的木构件咬合成长方体,则咬合时带卯眼的木构件的俯视图可以是( )

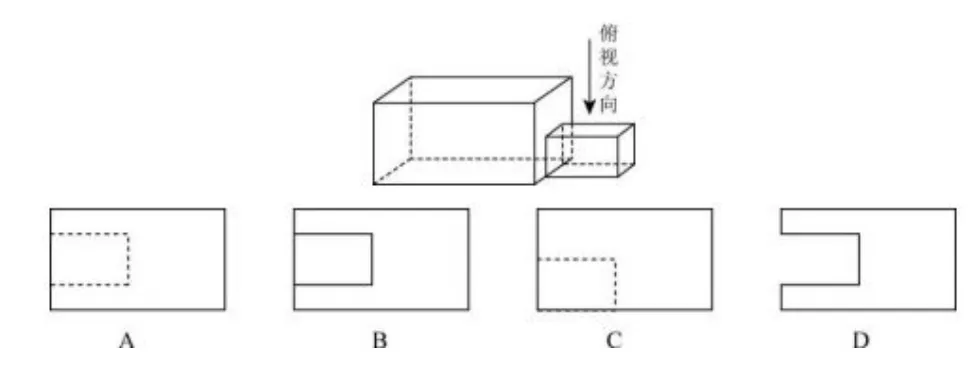
图2

赏析这个问题以优秀的中华木土文化为背景,以古建筑中的榫卯为载体,结合立体几何三视图基础,从更高的要求和不同的角度,考查考生的空间想象能力和空间图形的转化能力.这样设计可以让学生体会到我们古代数学的优秀传统——数学要关注生产、生活等社会问题,引导师生了解数学文化和数学史,体会数学知识在认识世界中的工具作用.

例3(2017 全国卷2 理3)我国古代数学名著《算法统宗》中有如下问题:“远望巍巍塔七层,红光点点倍加增,共灯三百八十一,请问尖头几盏灯? ”意思是: 一座7 层塔共挂了381 盏灯,且相邻两层中的下一层灯数是上一层灯数的2倍,则塔的顶层共有灯( )

A.1 盏 B.3 盏 C.5 盏 D.9 盏

赏析此题从古代数学名著《算法统宗》引入,然后通过诗歌提出数学问题,考察等比数列的基础知识,先利用等比数列前n 项和公式求出首项,然后利用等比数列通项公式求第7 项.本来一个非常简单的等比数列问题,在数学史背景的衬托之下,具有一定人文特色,这种基于数学史的高考试题,对学生的数学阅读能力也有较高的要求,这将引领师生在数学教与学活动中更多地关注数学史等元素.

例4(2016 全国卷2 理8)中国古代有计算多项式值的秦九韶算法,右图是实现该算法的程序框图.执行该程序框图,若输入的x = 2,n = 2,依次输入的a 为2,2,5,则输出的s=( )

A.7 B.12 C.17 D.34

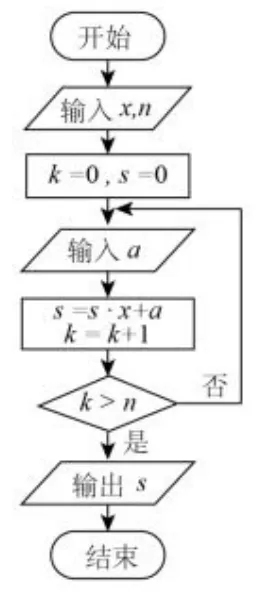
图3

赏析秦九韶是我国古代数学家的杰出代表之一,其《数书九章》概括了宋元时期中国传统数学的主要成就.其中的秦九韶算法是一种将一元n 次多项式的求值问题转化为n 个一次式的算法,大大简化了计算过程,即使在现代,利用计算机解决多项式的求值问题时,秦九韶算法依然是最优的算法,大大提高了计算的时间复杂度.本题以秦九韶算法为历史背景,不仅可以让学生理解数学历史文化,形成理性思维,同时也能学生感受我国古代数学的成就,增强爱国情怀.

4、思考

不难发现,基于数学史的高考数学试题常与概率、立体几何、数列、算法等知识有关,解题的关键是将数学史背景下的条件转化为高中数学知识,考察考生的阅读理解能力、抽象概况能力、转化与化归能力,既体现了对数学应用性的考察,也体现了我国数学文化的源远流长.因此,挖掘高考试题中的数学史背景,并有效应用于教学,是将数学史和高中数学教学结合的有效途径.具体思考如下:

4.1 为新课程标准的教学改革添砖加瓦

基于数学史的高考数学试题,素材新颖、构思精巧、立意高远、视角独特、导向鲜明等特点都充分体现了新课改的理念.高考试题中蕴含数学史的深意,绝不是单纯要“秀”几道题这么简单, 中学教师应加强数学史对数学新课改的影响,为此教学中应该重视教学史的教学与反思,使数学史的应用深入到学生的认知层面,这样做不仅可以启发学生思维,帮助学生掌握学科体系,而且可以激发学生学习兴趣,培养学生的数学思维能力和数学问题意识.可以预见,数学史是一座有待开发的宝山,有待于我们从多角度多方位进一步开发,进而引导高中数学教学方式的改变,为新课程标准的教学改革添砖加瓦.

4.2 重视数学史中的数学过程,利于对学生数学素养进行科学评价

高考试卷中出现基于数学史的题目,有利于我们更好地评价学生的数学学习.目前为止,对学生的评价依然是以高考成绩为主,过去我们一直强调数学的人文价值,但是考试却从来不会考,也不知道如何去考.但是,现在的高考试卷数学史部分恰恰考查了学生的数学人文素养,这是对高考数学试题的大胆创新,符合新课程改革的精神与方案.这样能够对学生的数学素养作出了全面与综合的评价,是值得肯定与推广的.

4.3 重视教材中的数学史材料,让数学史与日常教学有机融合

张奠宙教授指出:“数学史必须走进课堂,在实际教学中使得学生在学习数学的过程中真正感受到文化感染,产生文化共鸣,体会数学的文化品味和人情味.”目前,数学史已经进入中学生的数学教材,高中教材中涉及的数学史的总量比较多,内容比较丰富,并且和数学的基本知识联系紧密,一共设计了46 个数学史,具体分布如表2 所示.

表2 数学史在各必修教材中的分布[4]

可以看出新课程在教材编排上渗透了大量与学生所学数学知识相关联的数学史的内容,内容覆盖面相对以往的教材来说更加广泛,更有利于教师进一步发掘教材,加工教材,从而增加数学课堂教学的趣味性,为激发学生的兴趣提供了新的契机,同时也提醒我们在未来中学数学教师日常的教学过程中要更加注重数学史的渗透,做到有机融合,让学生认识到数学不仅是一门科学,更是一种文化,同时,数学史的知识同中学数学教育相结合可以使学生的学习取得事半功倍的效果.