让图形来“说话”
2019-04-12丁群俐蔡水华
丁群俐 蔡水华

摘 要:
几何直观是《数学课程标准》提出的十大核心概念之一,本文从寻找直观模型、注重自主操作、加强数形结合等教学策略出发,帮助学生直观地理解数学问题的本质,让几何形体在学生头脑中从“简约”走向“丰盈”,以求更有效地培养学生的空间观念和几何直观能力。
[关键词 ] 几何直观;数学图形;数学教学
著名数学家华罗庚说:“形缺数时难入微,数缺形时少直观。”几何直观是揭示现代数学本质的有力工具。培养几何直观能力的策略有很多,本文从几何直观教学策略的角度出发,帮助学生直观地理解數学问题的本质,有效地培养学生的空间观念和几何直观能力。
一、寻找直观模型,发展学生的直观洞察力
1.以图表思,形象直观。《数学课程标准》指出:几何直观主要是利用图形描述来分析问题。通过图形将关键信息传达出来,能帮助我们有效地思考问题、分析问题,寻求解决问题的方案。因此教师要善于借助几何直观,画一画、涂一涂,以图导思,让解题思路一目了然。
有这样一道题:有一堆货物共9600千克,需要2辆车分4次运完,那么每辆车每次运多少千克?
在解决问题前,教师提出要求:先列算式,然后在长方形图中画出解题思路。
反馈时,学生的回答很精彩:
学生通过分长方形来表示算式每一步表达的含义,清晰地描述了解题思路。教师较好地利用长方形沟通了解决问题、计算教学与空间图形三者之间的关系,充分利用外化的“形”把内在的数学本质形象地表示了出来。
2.以图促思,表征直观。几何直观不仅应用于“图形与几何”的教学,在其他领域也发挥了不可替代的作用,而且贯穿于整个数学学习的过程中。它凭借图形的直观性特点将抽象的数学语言与直观的图形语言有机地结合起来,深入数学问题的本质,打开学生思维的大门,帮助学生理解数学知识的难点。
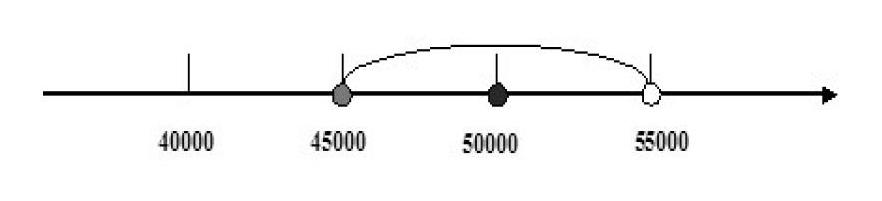
一个数的近似数是相对抽象的一个概念性知识,在作业中有这样一道题:甲、乙两个数,将甲数四舍五入省略万后面的尾数约是5万,将乙数改写成以“万”为单位的数是5万,那么甲数和乙数的大小关系是()。
A.甲数=乙数B.甲数>乙数
C.甲数<乙数D.无法确定
在解答这道题时,不少学生是举例说明的,列出了两个不同的数来比较,而有一个学生用数轴来表示,这样就把其他同学说的情况都包括进去了。
从这道题的分析中,我们可以发现,数轴这种特定的几何图形在数与代数领域淋漓尽致地发挥了几何直观的作用,之前几个同学说的都是零散的数,而这个同学利用数轴一下子把大家的思维聚焦起来,将这些数与数轴上的点一一对应起来,学生的思路也开阔了,而且这样比较更方便、更直观。
二、注重自主操作,发展学生的空间想象能力
1.借助自主操作,积累表象经验。要培养学生的几何直观能力,不能光是教师画,而要让学生积极参与,自主操作。让学生经历用图形来描述问题和分析问题,以达到解决问题的目的。
在教学“植树问题”时,有位教师一开始就提出了一个比较开放的问题:在学校门口一条长20米的马路一边,每隔5米种一棵树,能种几棵树?
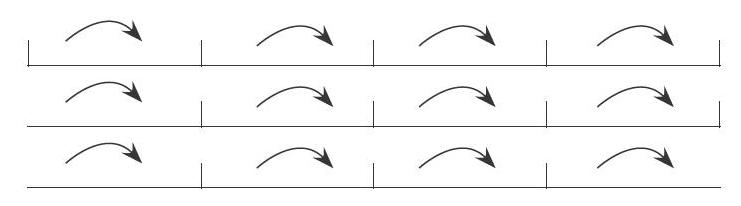
当学生得出不同答案时,教师没有马上下结论,而是让学生画图验证自己的猜想:
根据这三幅图,学生发现:当两端都种时,棵数=间隔数+1;只种一端时,棵数=间隔数;两端都不种时,棵数=间隔数-1。
植树问题是比较抽象的问题,学生理解起来比较困难。学生通过直观图找到了各数量之间的关系,找到了解决问题的方法。通过画线段图,增强了学生对植树问题的感性认识,有效地帮助学生理解了间隔数与棵数之间的复杂关系,积累了数学活动的经验。
2.借助图形,发展空间联想。随着年龄的增长,学生从生活中获得了不少经验,形成了一定的空间知觉和空间表象。在教学中教师可以借助直观图形,引导学生进行合理猜想,充分发挥学生的空间想象能力。
在学习“分数的认识”时,有一道这样的题目:图1中阴影部分可用[13]表示吗?
学生看到这个图马上会判断是错的,因为它没有平均分。
师:那这三份都不可能是[13]吗?
师:中间那份真的是整体的[13]吗?你们有什么好方法验证一下?
学生边观察图形,边拿起笔思考。
在交流中,学生中出现了两种思路,他们结合画的草图将想法清晰地表达出来。
在教学分数的意义时,我们发现,如果在课堂上大量使用“平均分”的分割线,在帮助学生形成分数概念的同时也对分数概念本质的理解起到了干扰作用。学生会认为只有分割成大小形状一样的图形才能被称为“平均分”。在这个教学片段中教师引导学生根据三角形图形进行探索、观察、操作、验证,使学生对分数概念的本质有了更深刻的理解,思维也得到了很大程度的提升。
三、加强数形结合,提高学生的解决问题能力
1.以形助数,内化解题思路。在解决问题时,经常会发现学生找不到思路,或者列出了算式却说不清楚解题方法,这时我们可以借助形象化的直观图形来帮助学生提取信息,找到解决问题的方法。
例如,一个底面是正方形的长方体,把它的侧面展开后得到一个边长是12厘米的正方形,求这个长方体的体积是多少?
初看这题似乎缺少条件,教师让学生先根据信息画图(如图2),将已知条件表示出来。
当学生画出展开图后,发现长方体的高就是12厘米,长和宽都是12÷4=3厘米,这个隐含的信息找到后自然就能求出长方体的体积。
在图形与几何的学习中,我们常常会碰到诸如此类的问题,学生往往不能直接找到相关的数据解决问题,这时画图就是一种很好的解题策略,可以帮助学生理清思路,找到隐含信息,从而解决问题。本案例中的图形语言为数学思维活动提供了直观模型,从而达到以形想数、化难为易、化隐为显的目的。
2.数形互译,外显数量关系。数量关系是在具体情境中抽象概括出来的,具有高度的抽象性。教师可以借助几何直观的方法帮助学生理解和诠释数量关系,化抽象为直观,化内在为外显,为学生在分析数量关系与解决问题之间搭起一座桥梁。
有这样一道应用题:一块长方形菜地,长与宽的比是7∶3,如果长减少12米,宽增加16米,就变成了一个正方形。这块菜地的面积是多少?
学生解答这道题时感觉无从下手,教师引导学生画出如下的线段图(如图3):
学生借助线段图更直观地理解了“长比宽多出来的4份,就是16+12=28米”的结论。此时数量关系很明确,问题也就迎刃而解了。
内在的解题思路形象地外显了,这样的图形直观明了,易于理解,数形互译,有效地凸显了数形结合思想。
几何直观可以帮助学生直观地理解数学问题的本质,在表征直观、读懂直观中可以进行推理和想象,实现思维的顿悟。当然,几何直观能力的培养并不是一朝一夕的事,在教学中我们要根据学生的认知规律,采用合理的教学方式,促使学生对几何形体有深刻的认识,使几何形体在头脑中从“简约”走向“丰盈”,有效地培养学生的空间观念和几何直观能力。
