论高中数学“数形结合”在解题中的应用

张雨

摘要：在高中数学学习过程中，“数形结合”的题目较为常见，我们要从题目中总结数学思想，以保证解题效果更好。“数形结合”不仅仅是一种数学研究方法，也是解决抽象数学问题的关键，需要我们认真学习。

关键词：高中数学;“数形结合”;解题应用

在高中数学中，“数形结合”一般能直观辅助进行填空题或者是判断题解答，能在减少解题难度的基础上，提高解题效率，具有非常实用的价值，老师常常指导我们要在实际学习过程中系统化应用“数形结合”的思想，开发自己的数学思维。

一、集合问题中应用“数形结合”思想

在高中数学中，集合问题较为常见，无论是在选择题中较为简单的集合类题目，还是在大题中，若是仅仅将集合答案进行分析来判定集合的解集，然后在合并计算，不仅会增加计算量，也会导致计算过程出现重复，这严重影响我们的解题效率。甚至会出现重复计算造成的错误，使得相应的题目不能有序推进。基于此，我们就要利用“数形结合”的方式提高解题效率，为保证解题准确性和基本速度奠定基础。目前较为有效的“数形结合”就是Venn图。

例题01：若是某个学校组织课外活动，将一个班级内的50名学生分为不同小组，其中，参加语文鉴赏兴趣小组的人数为30人，参加化学实验小组的人为26人，共同参加语文鉴赏和化学实验兴趣小组的人员为15人，试问班级内有哪些同学既没有参加语文鉴赏组也没有参加化学实验小组[1]。

解答过程，这是一道非常典型的集合类题目，在常规化解题思路中，会利用两个兴趣小组人数减去15人，得出参加活动的人数，利用减法就能计算出最终的人数。但是，若是利用“数形结合”就能直接將相关数据代入到Venn图中，迅速得出相应的结论。

也就是说，借助“数形结合”能直观进行数字和形状的组合，提高数据的直观性，有效提高计算效率，为后续计算结果的优化奠定基础。

二、函数问题中应用“数形结合”

函数学习一直是非常困难的学习难点，无论是解题思路还是解题过程都较为复杂，涉及的知识点较多，我们要想提高自己的学习效率，就要对具体问题进行具体管控，有效结合具体知识结构完善解题思路。需要注意的是，在函数解题过程中，传统的解析法、列表法都能有效完成相应的数据关系，只有借助图像法才能对具体问题进行统筹分析，合理性显示出不同要素之间的关系，保证最值、定义域以及零点等问题都能得到有效处理，保证解题效率。

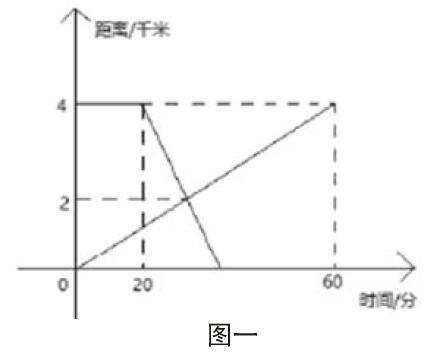
例题02：已知有A、B两地之间的距离为4km，在早上8：00，学生m从A地出发步行到B地，与此同时，在8：20的时候同学n从B地向着A地出发，学生n是骑自行车，图形表示的是学生m和n两个人在距离A地和所用时间之间的关系，试问，学生n到达A地所需要的时间。

解题过程：结合图形可知，从原点出发的运行路线就是学生m的路线图，另外同一条线就是学生n，就能结合相关数据求解具体问题。

借助题目不难发现，原本较为复杂的关系，借助图形进行表述后，相互关系就显而易见，我们能借助图形对相关数据之间的关系有明确的认知，且能直观描述出不同参数结构之间的关系，并且保证数据分析和计算过程的完整性，有效提高计算效果和综合效率。因此，我们在高中数学学习过程中，要有效对具体问题进行具体分析，合理性绘制相应的“数形结合”组合图形，保证解题效果的合理性[2]。

三、解析几何中应用“数形结合”

在高中数学各个教学模块中，以解析几何中应用“数形结合”作为常见，应用数形结合的目的就是将一些抽象以及复杂的问题简单化以及直观化，从而有效建立相应的几何关系。需要注意的是，在高中数学知识结构中，几何体系设计范围较多，简单的几何图形数据关系还比较简单，但是在一些立体图形分析过程中，要将不同计算过程和演化过程进行融合和处理。也就是说，在具体题目解析的过程中，我们要有效应用“数形结合”的思想，保证能借助向量判定空间几何内容，一定程度上将复杂的问题简单化，有效判定更加合理的数据关系，应用相应的关系结构和参数体系提高解答效果。最重要的是，我们在实际学习中要紧跟老师的思路，充分优化解题方式，并不是借助想象完成解析几何的具体题目，而是要应用“数形结合”的方式将相关数据关系落实在题目中，有效提高解题效率和准确性，并且一定程度上提高计算的基本水平。

四、三角函数中应用“数形结合”

高中数学中三角函数也十分重要，主要是因为其题型变换较多，尽管计算难度并不大，但是，一部分题目较为抽象，若是单一化利用数据信息的分析往往很难有效判定相关数据之间的关系，这就需要在实际解题过程中合理性应用“数形结合”的思想，建立相应的数据关系，确保能有效发挥“数形结合”的计算优势，提高计算准确性和数据关系判定的合理性[3]。

也就是说，在三角函数题目解答的过程中，要将重点落实在三角函数中单位圆三角函数线以及三角函数图像分析方面，对定义域以及单调区间求解等问题进行系统化分析，确保能借助图形讨论相关问题。例如，在比较大小的题目中，借助图像就能有效进行判定，不仅仅能减少解题时间，也能在拓宽我们学习思路的基础上保证解题准确性。

五、不等式中应用“数形结合”

在高中数学中，我们在数轴学习过程中是首次接触“数形结合”解题理念，能将相关数据和关系集中在数轴中展现出来，合理性判定实数的范围或者是判定相应数据的大小。并且，能借助直观的数轴对相关数字之间的关系进行分析，合理性证明不等式。

结束语：

总而言之，在教学改革不断推进的背景下，高考数学的题目将更加多样化，我们要积极转变自己的学习思路，我们要清晰地梳理相关内容，保证学习效率，进一步提高自身的观察能力和总结能力，拓宽学习和解题思路，有效应用“数形结合”的思想进行解题，提高自身的数学学习能力，优化解题水平，为更好地迎接高考做好准备。

参考文献：

[1]高成语.浅谈数形结合在高中数学中的应用技巧[J].中学课程辅导（教学研究），2018，12 （5）：181.

[2]罗崇煜.基于数形结合思想的高中数学应用研究[J].黑龙江科技信息，2017 （6）：32-33.

[3]邓雅文.运用数形结合巧解高中数学解析几何问题[J].科学技术创新，2018 （3）：55-56.