非等边三面角反射器RCS的解析表达与有效散射区域分析
2019-04-12闫华李胜殷红成
闫华,李胜,殷红成
(1.中国传媒大学信息工程学院 北京 100024;2.电磁散射重点实验室,北京 100854)
1 引言
在较大入射角度范围内,三面角反射器能将入射电磁波反射到相反的方向上去,从而具有较强的后向雷达散射截面积(RCS)。正是由于该优点,三面角反射器被广泛应用到雷达标定、雷达干扰、海上搜救、雷达目标物理模拟等领域[1][2]。另外,三面角结构普遍存在于车辆、舰船等实际人造目标中,是目标散射特性的主要贡献源。因此,研究三面角反射器的散射特性具有重要的实用价值。
三面角反射器主要由三个相互垂直的平板构成,较为常用的三面角反射器包括正方板角反射器、三角板角反射器和圆板角反射器[2]。由于它们都是采用完全相同的三块平板组成,所有它们均属于等边的三面角反射器。一些经典著作与若干文章对等边三面角反射器的RCS进行了详细的探讨[3]-[6],给出了RCS计算公式、半功率点宽度和全姿态角平均RCS值等特性。尽管如此,实际目标中的三面角结构都属于非标准的、非等边的三面角反射器,因此需要研究非等边三面角反射器RCS特性及计算公式,但关于这方面的工作相对较少。文章[7]通过一些类典型体散射的解析式来表征复杂目标用于SAR目标识别,但典型体中三面角仍然采用标准的等边角反射器结构,从而造成其RCS在大角度范围内偏离实际目标中的非标准三面角反射器结构。本文作者在前面的文章[8]中给出了非等边的三角板角反射器和正方板角反射器RCS的解析计算公式,并通过电磁仿真数据进行了验证,但文中没有给出详细的推导过程,而这在新型RCS模拟单元设计等一些感兴趣的研究和应用场合往往是必要的。本文将针对非等边三角板型三面角反射器,给出RCS计算公式的详细推导过程,并着重分析对目标后向RCS具有实际贡献的有效散射面积。
2 理论推导
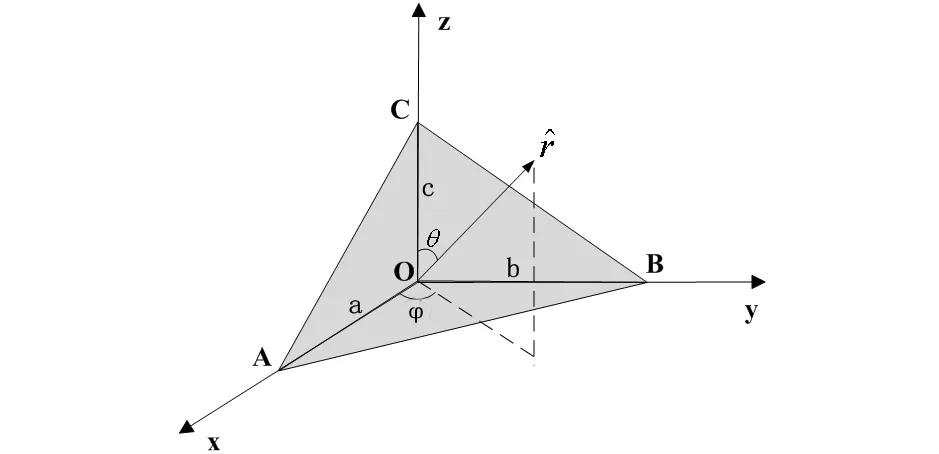
图1 三面角反射器几何外形、坐标系与雷达方向等参数的定义

rx=sinθcosφry=sinθsinφrz=cosθ
(1)
根据文献[3],一般的三面角RCS可以表示成一等效平板RCS,计算公式为:
(2)
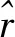
(3)
其中
l=min{rx,ry,rz}m=mid{rx,ry,rz}n=max{rx,ry,rz}
(4)
min{·,·,·}、mid{·,·,·}、max{·,·,·}分别表示取括号内三个元素的最小值、中间值和最大值。
对于一般的非等边三面角情形,(3)不再适用,下面将基于几何光学(GO)法推导其解析形式。推导过程分成三个步骤,首先给出直线传播射线的投影变换公式和单次弹射射线的方向变换公式,详见2.1节和2.2节;其次,基于前两节得到的公式推导射线经过三面角三个面的三次弹射过程中弹射点之间的投影变换矩阵和方向变换公式,详见2.3节;第三,确定有效散射区域,详见2.4节;最后,给出等效散射面积Seff的解析表达式,实现非等边三面角反射器的解析表示,详见2.5节。
2.1 直线传播射线的投影变换公式
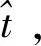
(5)
其中s为路程参数,此时,位置矢量P表示成单参数s的函数。 式(5)的分量形式为:
x=x0+stxy=y0+styz=z0+stz
(6)
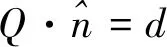
(7)
写成坐标的线性方程:
nxx+nyy+nzz=d
(8)
设入射射线在平板Ф上的弹射点为PΦ,则反射点PΦ可由式(6)和(8)确定,将式(6)代入(8),有
nx(x0+sΦtx)+ny(y0+sΦty)+nz(z0+sΦtz)=d
(9)
于是,可以得到反射点的s参数值:

(10)
由于反射点PΦ可以表示成
(11)
则将(10)代入(11),可得射线投影公式:
(12)

(13)
2.2 单次弹射射线的方向变换公式
(14)
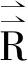
(15)
2.3 三次弹射射线的投影变换公式与方向变换公式
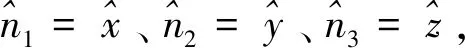
显然,对于三面角的三次弹跳射线,存在着6种射线传播路径:S1→S2→S3、S3→ S2→ S1、S1→ S3→ S2、S2→ S3→ S1、S2→ S1→ S3、S3→ S1→ S2。
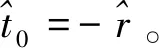
(16)
(17)
同样,第二次在S2上发生镜面反射的弹射点与反射射线方向
(18)
(19)
同样,第三次在S3上发生镜面反射的弹射点与射线方向
(20)

(21)
假设第三次反射射线投射到一个垂直于射线方向并且通过O点的平面(记为S4)上,于是
(22)
也就是说,PS4与P0在平面S4上投影两者对于O点对称(即互为中心反演)。
另外,根据上面的推导,定义投影变换矩阵
(23)
(24)
(25)
(26)
分别对应特定射线轨迹上的点从P0→ S1、S1→ S2、S2→ S3、S3→ S4的映射矩阵。显然,平面S1、S2、S3中的线段之间的变换关系仍然满足这四个映射矩阵。
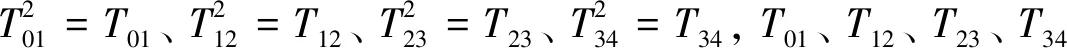
2.4 投影到平面S4上的等效散射区域
三面角反射器的三个三角板S1(三角形OBC围成的区域)、S2(三角形OAC围成的区域)、S3(三角形OAB围成的区域)分别沿射线传输路径S1→S2→ S3→S4向面S4投影。
首先,面S3(OAB)沿射线路径S3→S4直接投影到S4面上得到三角形区域OA′B′,此时需要考虑投影矩阵T34,则投影点A′、B′的坐标是
(27)
(28)
其次,面S2(OAC)沿射线路径S2→S3→S4经一次反射投影到S4面上得到三角形区域OA″C″,此时需要考虑投影矩阵T234=T34T23,则投影点A″、C″的坐标为
(29)
(30)
也就是说投影点A″与A′重合,C″为C′关于O点的中心反演。
最后,面S1(OBC)沿射线路径S1→S2→S3→S4经二次反射投影到S4面上得到三角形区域OB′″C′″,此时需要考虑投影矩阵T1234=T34T23T12,则投影点B′″、C′″的坐标为
(31)
(32)
也就是说投影点B′″、C′″分别为B′、C′关于O点的中心反演。
图2给出了三个三角板区域S1、S2、S3沿射线传输路径S1→S2→ S3→S4在面S4上的投影。其中,三角形OA′B′为OAB在S4面上的投影区域;三角形OA″C″为OAC在S4面上的投影区域;三角形OB′″C′″为OBC在S4面上的投影区域。显然,所有沿三次弹射路径S1→S2→ S3→S4的出射射线对应三个投影区域OA′B′、OA″C″、OB′″C′″的重叠区域(即图中粉色区域),该区域即为投影到S4面上的有效散射区域,其面积为路径S1→S2→ S3→S4所对应的等效散射面积。
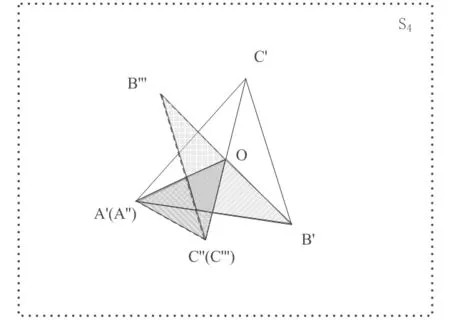
图2 沿着S1→S2→S3→S4路径传输射线的等效散射区域 (即OA′B′、OA″C″、OB′″C′″三者的重叠区域)
对于其它5种路径,可以进行类似的分析。综合考虑所有的6种路径,可以得到如图3所示的等效散射区域。三面角三次反射的有效区域为三角形ABC在S4上直接投影的三角形区域A′B′C′、ABC经一次反射在S4上投影的六边形区域A′C′″B′A′″C′B′″,以及ABC经二次反射在S4上投影A′″B′″C′″(即A′B′C′关于O以雷达视线为轴的中心反演)三者之间的重叠区域(六边形区域)。重叠区域的面积即为三面角反射器的总等效散射面积Seff。下一小节将计算这个等效散射面积Seff。
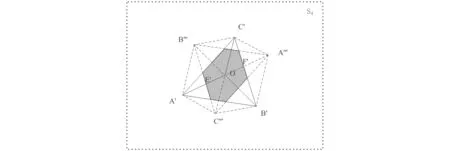
图3 三面角反射器总等效散射面积 (即投影的三角形区域A′B′C′与A′″B′″C′″的重叠区域,A′″B′″C′″可由A′B′C′绕O点以雷达视线为轴旋转180°所得到)
2.5 等效散射面积的计算公式
由非等边三面角的直角边长为a、b、c,则三个三角板的面积为
(33)
于是,对于A、B、C在S4上的直接投影A′、B′、C′,有
(34)
(35)
(36)
则一次弹射投影区域A′B′C′的面积为

(37)
如果设
wx=bcrx,wy=cary,wz=abrz
(38)
于是,式(34)-(37)变为
(39)
(40)
(41)
(42)
由于等效散射面积Seff等于SA′B′C′减去三个小三角形(分别以A′、B′、C′为顶点的小三角形区域,记为SA′m、SB′m、SC′m)的面积。
先来计算SA′m。设A′A′″分别与B′″C′″和B′C′交于E′和F′(如图3所示),有
(43)
由于显然有|OE′|=|OF′|,则
(44)
即
(45)
同理,对于SB′m和SC′m有
(46)
(47)
于是,有效面积Seff为
(48)
实际上,上面的推导隐含了条件A′、B′、C′在三角形ABC的外面,此时有
l+m≥n
(49)
其中
l=min{wx,wy,wz}=min{bcrx,cary,abrz}m=mid{wx,wy,wz}=mid{bcrx,cary,abrz}n=max{wx,wy,wz}=max{bcrx,cary,abrz}
(50)
其中雷达视线方向分量(rx,ry,rz)由式(1)给出。
那么,当(49)不满足时,例如,当wy+wz≤wx,等效面积Seff应为
(51)
考虑,一般的情况
l+m≤n
(52)
满足时,有
(53)
于是,总结一下式(48)和(53),非等边三角板型三面角反射器的等效散射面积为
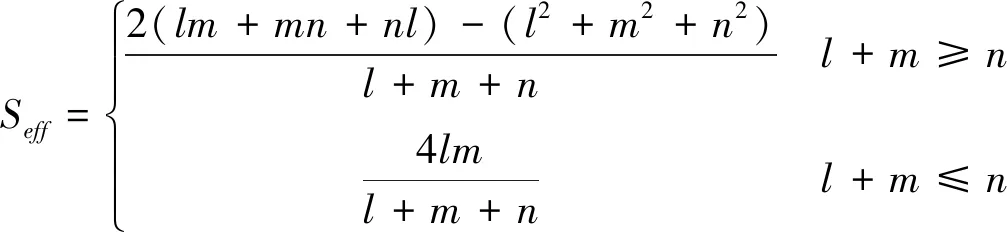
(54)
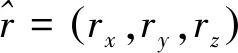
得到了等效散射面积Seff,由公式(2)即可计算非等边三角板型三面角反射器的RCS值。
3 在三个板面上的有效散射区域
2.4节给出的是投影到平面S4上的等效散射区域,下面进一步分析三面角反射器的三个板面上的有效散射区域。
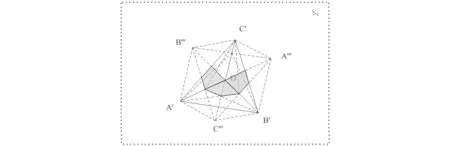
图4 传播路径S1→S3→S2和S2→S3→S1上的射线集经过的三个三角板面的有效散射区域(标黄色的区域)
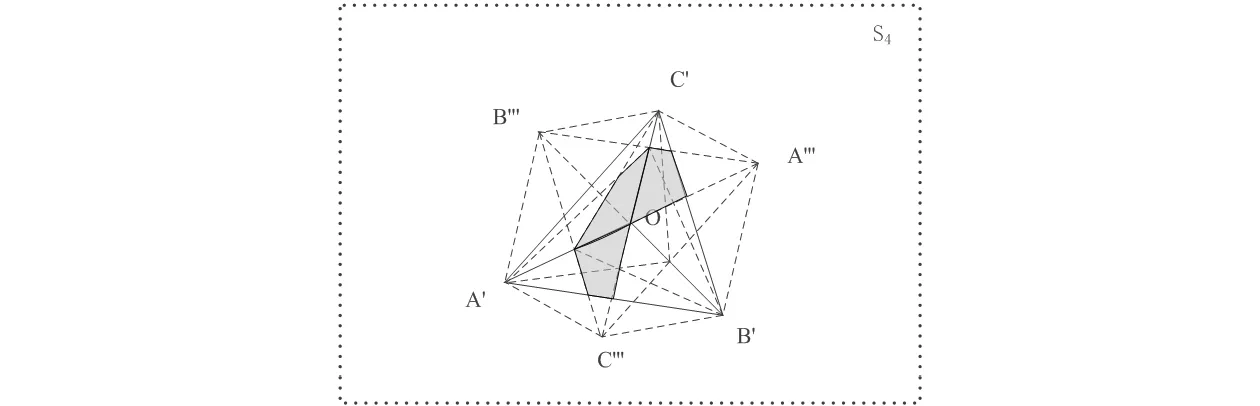
图5 传播路径S1→S2→S3和S3→S2→S1上的射线集经过的三个三角板面的有效散射区域(标绿色的区域)
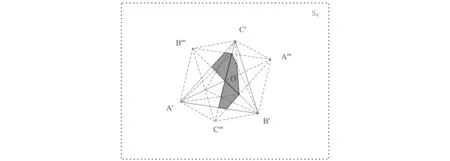
图6 传播路径S2→S1→S3和S3→S1→S2上的射线集经过的三个三角板面的有效散射区域(标红色的区域)
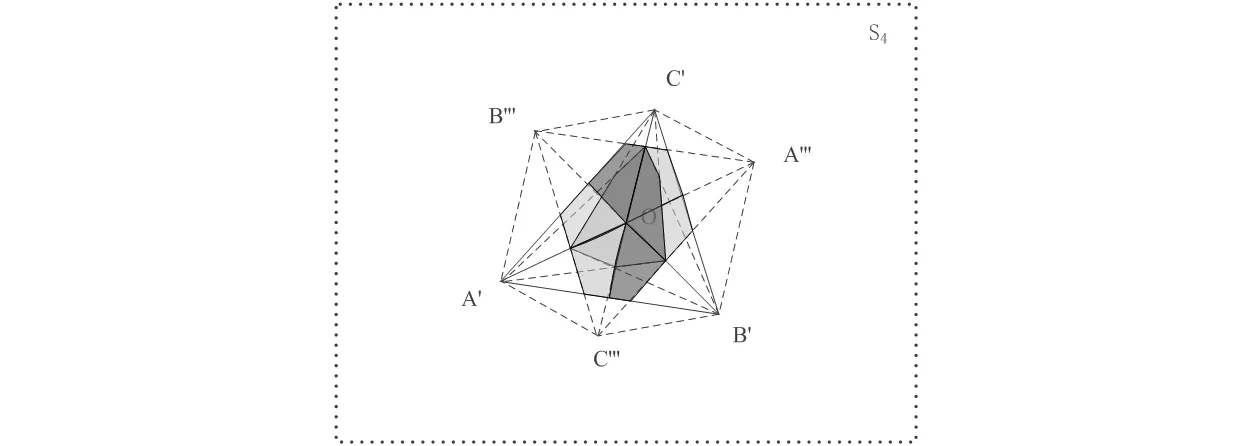
图7 所有传播路径的所有射线经过的三个三角板面的有效散射区域(标不同颜色的区域,与图4-6中的颜色定义相同)
由于6个传播路径上存在着两两互为可逆的传播路径,而可逆的传播路径经过三个板面的有效散射区域是相同的,因此图4-6分别针对每一对可逆传播路径给出了射线集经过的各三角板平面的有效散射区域(以在S4平面上投影的方式显示)。从图中可以看出,在特定可逆传播路径下不同板面的有效散射区域的位置存在差异。例如图4所示,OAC和OBC上的有效散射区域为以OA和AC上线段为边的四边形区域,而OAB上的有效散射区域则是以OA和OB上线段为边的四边形区域,该区域靠近三面角的顶点O。图5、图6的情况类似。如果将图4、图5、图6所对应的三个有效散射区域合并在一起显示,如图7所示,可以看出,三个板面靠近三面角顶点O的区域对两组互逆传输路径的射线起作用,而远离三面角顶点O的区域只对一组互逆传输路径的射线起作用。因此,如果三个板面靠近三面角顶点O的区域发生变化,对目标的RCS将产生更大的影响。该分析结果可为三面角反射器的新型改进设计提供依据。
4 结论
本文针对非等边的三角板型三面角反射器,基于几何光学原理详细推导了角反射器RCS计算公式。在推导过程中,根据几何关系确定了对目标后向RCS具有实际贡献的等效投影区域,得到了等效散射面积的解析表达形式。本文也分析了三面角反射器三个板面上的有效散射区域,以及不同位置对目标RCS贡献的重要程度。本文的方法与结果对目标识别中目标三面角结构的几何特征提取以及目标特征控制中三面角反射器的改进设计等应用具有指导意义。
