模糊厌恶投资者的一般性默顿问题研究*

陈 琳， 陈晓燕

(南京理工大学 理学院，南京 230000)

0 引 言

传统上，金融建模非常依赖于基础概率测度P的选择，它用于获得市场价格变化的统计性和随机性。早在巴舍利耶、布莱克和斯科尔斯、默顿和萨缪尔森的作品中，股票价格和利率这样的风险因素已经被建成在P下的马尔可夫扩散模型。但全球经济和金融动态的复杂性使得我们不能准确识别风险因素的演变，并且金融建模本身就不可避免地受到模型模糊性的影响。

在过去20 a年中，投资组合优化的核心问题已被在多个先验背景下进行了广泛研究。若投资者对投资问题抱有悲观看法，那么可以采取极大-极小方法解决问题，即首先将效用函数最小化，然后最大化投资策略，通过所谓的模糊厌恶偏好，这种悲观行为已经完全被公理化。

在SaraBiagini的论文[1]中，投资者具有CRRA效用且对平均收益率和波动率估计存在疑虑，该文研究了模糊厌恶投资者的稳健默顿问题，并扩展了经典的默顿问题。本文以Sara Biagini[1]的论文为基础并进行了一些改进。因为 CRRA效用函数和CARA效用函数都是凹函数，所以它们都可以表明投资者是厌恶风险的。本文可以得出与Sara Biagini的论文不同的结果并提供投资默顿问题的明确解决方案。

假设资产价格过程是一维扩散且含有一维维纳过程。投资者对漂移和波动率的估计存有疑虑，并认为给定紧集K中存在所有瞬时波动率，集合K必须满足唯一要求，即对于给定的过程σ，代理人认为所有漂移均在此区域中取值：

这里ε≥0 是模糊半径。本文的结构如下：第1节介绍了非主导情况下消费投资问题的具体模型，且这个稳健问题可以看作是代理人和不利市场两个参与人之间的零和游戏；在第2节中，为了求出具体解，关注具有CARA效用的代表性投资者的情况；第3节求得一般稳健问题的具体解决方案。

1 模糊厌恶下的一般默顿问题

1.1 经典默顿问题

假定代理人投资一项风险资产和一项无风险资产，且投资行为处于布莱克-斯科尔斯-默顿市场模型假设下，也就是说, 无风险利率r是常数并且风险资产动态过程如下：

dSt=St(μdt+σdWt)

这里σ和μ都是常数，W是标准的一维布朗运动。

给定初始投资x>0，投资者允许以自融资的方式交易和消费。为了更具体地说明，令h=ht定义为一维循序可测过程，代表投资组合中资产的股份数，将c定义为消费流，财富过程X由以下随机微分方程给出：

dXt=(rXt+htSt(μ-r)-ct)dt+htStσdWt

由表示资产中的现金流过程θ来表达财富过程也是非常便利的，又θt=Stht，因此

dXt=(rXt+θt(μ-r)-ct)dt+θtσdWt

(1)

组合 (θt,ct) 对于式(1)中的解x是可容许的。

令Ap(x)是所有可容许组合的集合，给定时间度量T,代理人试图从集合中选择一组组合来最大化经营消费和终值财富的效用：

(2)

这类随机控制就是著名的默顿问题[2]。事实上，如果T趋近无穷大，那么效用值接近为0， 优化问题式(2)就变成如下情形：

假设1 效用函数u(0,)×R→(-,) 是可测的，对固定的t,u(t,x)是凹型，并且随着x递增满足稻田条件：

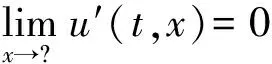
1.2 一般性默顿问题

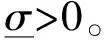
不确定的漂移假设为循序可测的[3]，对于给定的波动率，漂移允许在以下范围内变化：

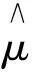
定义一个合理过程的集合：

r={(μ,σ)progr.meas.|σ∈S,μt(ω)∈U∈(σt(ω))}

定义1 合理的概率集P是在(Ω，F)上的Ps集合，过程S是SDE的唯一强解[5]：

这里的Wp定义为一个P-布朗运动，有 (μ，σ)∈r。

给定初始投资x>0，投资消费组合(θ,c)被称作稳健可容许的，即

Arob(x):=∩p∈PAp(x)

因此，给出X的P阶动态过程：

评论1 集合Arob(x)是非空的，事实上，可以展示它包含以下任何形式的策略：

θt=Xtπt,ct=γtXt

因而，X过程如下：

且X是Doleans指数:

模糊厌恶投资者会采取审慎的态度，此时投资者面对的默顿问题是：

(3)

SaraBiagini[1]已经证实式(3)中的价值函数V(0,x)是单调递增的且在R+是凹型。

引理1 假设存在一个函数v:[0,T]×R+→R，在 [0，T]×R+上连续，在[0,T]上C1,2，且有v(T,·)=u(T,·)；对任意 (θ，c)∈Arob(x) 都存在一个价值函数V(0,x)中内部极小值的最优解P(θ,c)，使得

(4)

引理1的证明是对Davis-Varaiya鞅最优控制原理的简单修改，详细过程可参考L.C.G.Rogers的Optimal Investment文献。

现在，使用随机微分验证方法来解决模糊性厌恶投资者的问题是非常直观的[6]。即给定一个具体的效用函数，寻找一个函数v满足引理1的前提条件，在P(θ,c)下使用伊藤公式，则式(4)过程Y满足以下SDE:

因此，得出一个极大-极小PDE：

(5)

这类公式为Hamilton-Jacobi-Bellman-Isaacs(HJBI)类型。

引理2 在假设1下，任意v∈C1,2且满足vx>0,vxx<0，式(5)的极大值和极小值都是可获得的[8]。Sara Biagini的论文为上述陈述提供了具体的证明过程，接下来是部分证明过程：

首先将σ固定的漂移最小化：

可以使用KKT得到最优解：

(6)

将式(6)代入式(5)中，可得出：

有最小化：

(7)

事实上，令集合s=θσ，则式(7)是对如下凹形抛物线式(8)的限制

(8)

通过对v的导数的符号考虑，顶点具有负横坐标，则式(7)的极小值可由最大的s得出。因此,argmaxKθ2σ2是最优σ的集合，则M(θ)：=max{θ2σ2|σ∈K}，得出

(9)

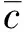
2 含有常数、非模糊性的稳健CARA效用问题

假设投资者有CARA效用，固定正常数ρ和λ,分别模拟时间不耐率和绝对风险厌恶，那么效用函数如式(10)所示：

u(t,x)=e-ρt(-e-λx)

(10)

在无边界的情况下，希望可以找到式(10)的解

(11)

假设式(11)可以得到有限值，且对一个固定的(θ,c)∈Arob(x)，内部的极小值可以得到，外部的极大值也可以获得，由结构性质暗示一个猜想，即价值函数会采用如下形式：

(12)

这里γε为待定的正常数。很容易验证v函数满足引理2的条件，可得出式(5)的最优解，用式(6)代替最优μ(θ)。为了对c进行优化，需引用u的双重凸函数：

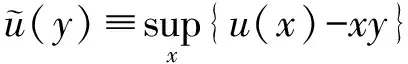
有u(x)=-e-λx使得

因此对c的优化发展为

代入式(12)可得：

假设

ψε(x,λ)=e-λγεx(-λγεx-1)

函数在θ是凹型的。若对θ优化，一阶求导为0是充分必要条件，因此优化后得出：

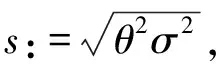
(13)

Hε:=H-ε

(14)

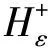
3 结 论

针对市场上的模糊厌恶投资者，在经典默顿问题的基础上，假设给定的波动率和求取漂移值的不确定性集，结合了哈密顿-雅可比-贝尔曼-艾萨克方程，并将其发展为极大-极小HJBI偏微分方程，最后求得了风险市场上的最优投资组合。