基于后悔理论的区间二元语义多属性群决策方法*
2019-04-11林文豪陈梅倩
林文豪, 陈梅倩
(安徽大学 数学科学学院,合肥 230601)
0 引 言
考虑到现实决策过程中决策者更倾向于给出语言决策信息来表达他对方案的偏好,所以大量学者对基于包括不同粒度的语言信息以及区间语言信息等多属性决策方法进行了大量的研究。Herrera等[1-2]提出关于语言信息集结后的二元语义分析方法,解决了一般语言信息集结后出现的信息损失和结果不精确问题;文献[3]提出在区间二元语义决策信息环境下利用离差最大化目标规划模型解决多属性群决策问题的方法;文献[4-5]对多粒度区间语言信息环境下的决策方法进行了研究,分别提出基于该信息环境下的TOPSIS群决策方法以及多粒度区间语言信息C-OWH算子的应用;文献[6]研究了二元语义偏好关系一致性偏差问题,并基于此提出了全新的群决策方法;文献[7]将区间语言信息拓展了,提出区间语言直觉模糊集并提出了新的信息熵TOPSIS决策方法;文献[8]提出了2TLCGPOWA算子并应用在多属性决策当中;文献[9]提出了把区间二元语义模糊信息与联系数相结合的决策方法。
后悔规避多属性决策方法是考虑决策者后悔规避心理的一种决策方法。后悔规避理论主要是对方案进行两两比较得到决策者对每一个方案的后悔和欣喜心理。
文献[10]针对属性值为区间数提出了考虑后悔规避的风险型多属性决策问题;文献[11]将后悔规避的决策方法拓展到了直觉模糊信息环境下;文献[12]基于后悔理论的思想,将后悔规避应用在了突发事件应急响应的风险决策当中;文献[13]将后悔规避与冲突风险熵理论相结合并应用于大群体应急风险决策中;文献[14]提出了考虑后悔规避的涉及多个行业的风险投资项目选择方法。
提出一种基于后悔理论的区间二元语义多属性群决策方法。首先,本文介绍关于区间二元语义信息,并给出了区间二元语义均值与方差的定义;然后针对决策矩阵元素为区间二元语义变量属性权重部分未知的多属性群决策问题,利用区间二元语义的方差构建优化模型确定最优属性权重;接着提出一种基于后悔理论的区间二元语义多属性群决策方法;最后将运用本文提出的方法帮助企业选择设计方案,并验证该方法的有效性和适用性。
1 预备知识
定义1 称二元组(sk,αk)为二元语言评价信息,其中sk为语言术语集里面的第k个语言变量,αk∈[-0.5,0.5]为符号转移变量,用来表示与评价信息sk的偏差。
定义2 设评价信息δ为实数,可通过函数Δ将δ转换为二元语义信息,其中,
其中round(δ)表示四舍五入取整算子。
定义3 设(sk,αk)为二元语义信息,则存在逆映射Δ-1,使得
Δ-1(sk,αk)=k+αk=δ
通过这样的映射使得任意一个二元语义信息转换成为实数。





(1)
由定义4与定义6给出区间二元语义信息加权平均算子:

在实际决策过程中,决策者给出的区间二元语义评价信息,往往带有一定的不确定性。正态分布作为一种常见的反应决策主观偏好的概率分布形式,在语言决策中有大量应用。因此,对于任意一个区间二元语义变量,不失一般性,考虑决策给出的区间语言评价信息服从一定的正态分布,首先给出区间二元语义信息的均值与方差的定义。

(2)
(3)
通过式(2)(3),下面给出一种区间二元语义的大小比较方法。

(1) 当μk1>μk2,则a1>a2;
(2) 当μk1<μk2,则a1 (3) 当μk1=μk2,则 1) 当σk1>σk2,则a1 2) 当σk1<σk2,则a1>a2; 3) 当σk1=σk2,则a1=a2。 一般情况下,决策者的决策行为会在不同程度上受到其他方案的影响,人们往往会将当前已取得结果与不同行为的结果加以比较,如果决策时选择另一种行为的结果会比现在好,那么个体就会产生后悔的情绪。著名的经济学家Loom, 卡尼曼等对其从经济学角度进行了大量的研究,而后悔理论在多属性决策中的应用相对而言较少,因此对其在语言决策中的应用具有理论和实际意义。 首先,设决策者给出的多属性决策矩阵为X=(xij)m×n,xij表示第i个方案在第j个属性下的评价信息。则基于后悔规避理论,决策者给出的不同方案在相同属性下的评价信息必定存在着差异,而这种差异便导致了决策者后悔的情绪。为了反映出不同方案相同属性下的后悔值与欣喜值,需要计算每一个方案在各属性下的效用值vij,本文采用文献[10]的效用函数: 其中β为风险规避系数,β∈(0,1),β取值越少,表示决策者风险规避程度越小;β越大表示决策者风险规避程度越大。 区间二元语义正态分布函数为 i=1,2,…,m;j=1,2,…,n 定义9 设v(xij)为决策变量xij的效用函数,f(xij)为决策变量xij的概率密度函数,则决策变量xij的效用值可以表示为 为了度量不同方案在相同属性下两两之间存在的后悔值与欣喜值情况,通过公式(4)来定量地计算出这种差异: (4) (5) (6) 其中σij为区间二元语义信息的方差,由式(3)可以计算求得。 下面给出基于改进的后悔规避理论多属性群决策方法步骤: 步骤3 利用模型式(6)以及步骤2中得到的方差矩阵求解各属性权重; 步骤4 利用式(4)和式(5)基于综合区间二元语言决策矩阵X=(xij)m×n计算出不同方案在同一属性下的两两之间的后悔值与欣喜值,构成后悔矩阵T=(tij)m×m与欣喜矩阵G=(gij)m×m。 步骤5 利用式(7)计算欣喜值S(Ai),利用式(8)计算后悔值R(Ai),利用式(9)计算折中值Q(Ai): (7) (8) Q(Ai)=γ(S(Ai)-S-)/(S+-S-)+ (9) 步骤6 将方案按照Q(Ai)的值从大到小一次排序,Q(Ai)值越大表明方案越优。 步骤7 结束。 对3位专家给出的区间信息矩阵进行集结得到新的区间二元语义信息决策矩阵X=(xij)m×n: 步骤3 利用lingo软件求解模型式(6)得到各属性权重为 ω=(0.1,0.4,0.2,0.2,0.1) 步骤4 经过分析本案例采用正态分布来确定效用值,其中取β=0.25,δ=0.3。利用式(4)和式(5)将区间二元语义决策矩阵转换成基于各属性下的后悔矩阵与欣喜矩阵(表1—5)。 表1 属性c1下的后悔矩阵与欣喜矩阵Table 1 The regret matrix and the rejoice matrix under attribute c1 表2 属性c2下的后悔矩阵与欣喜矩阵Table 2 The regret matrix and the rejoice matrix under attribute c2 表3 属性c3下的后悔矩阵与欣喜矩阵Table 3 The regret matrix and the rejoice matrix under attributec3 表4 属性c4下的后悔矩阵与欣喜矩阵Table 4 The regret matrix and the rejoice matrix under attributec4 表5 属性c5下的后悔矩阵与欣喜矩阵Table 5 The regret matrix and the rejoice matrix under attributec5 步骤5 利用式(7)计算欣喜值S(Ai),利用式(8)计算后悔值R(Ai),利用式(9)计算折中值Q(Ai): S(Ai)= (0.025 7,0.037 7,0.051 1,0.018 9,0.057 2,0.104 8) 步骤6 根据Q(Ai)对方案进行排序得 A6>A5>A3>A2>A1>A4 由排序结果可知方案6为最佳的生产方案。 步骤7 结束。 运用文献[10]中方法求解该问题: 步骤1 计算效用值; 步骤2 建立后悔矩阵与欣喜矩阵; 步骤3 对建立的后悔矩阵以及欣喜矩阵进行标准化; 步骤4 将每个属性下的后悔矩阵和欣喜矩阵相加,得到综合后悔矩阵以及综合欣喜矩阵; 步骤5 分别计算每个方案相对其他方案的综合后悔值以及综合欣喜值; 综合后悔值: (-1.046 3,-0.879 2,-0.701 2,-1.183 6,-0.519 1,-0.401 8) 综合欣喜值: (0.397 5,0.584 2,0.790 7,0.292 8,0.885 9,1.621 6) 步骤6 将综合后悔值与综合欣喜值相加得到综合排序值对方案进行排序,得到的结果为 Φ(Ai)=(-0.648 8,-0.295 0,0.089 5,-0.890 9,0.366 8,1.219 9) 排序结果为 A6>A5>A3>A2>A1>A4 由上面两种方法对比可以看出,两种方法的结果一致,所以本文提出的方法是可行的。该方法相比于过去提出的基于后悔规避的决策方法引入了新的信息表示形式,同时对于方案排序的方法不再是简单的集结,而是考虑了更多的人类行为心理因素,具有更加科学与实用的性质。 通过构建区间二元语义的方差优化模型确定最优属性权重,提出一种基于后悔理论的区间二元语义多属性群决策方法。该方法的可适用性广,可以应用于商业风险规避、企业风险投资决策等。同时也可以考虑应用到其他领域中,如投资决策、智能系统、资源管理等[15-16]。



2 基于改进的后悔规避多属性群决策方法
2.1 考虑属性权重部分已知的权重确定模型


2.2 基于改进的后悔规避多属性群决策方法步骤


(1-γ)(R(Ai)-R+)/(R+-R-)
3 案例分析
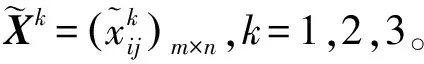





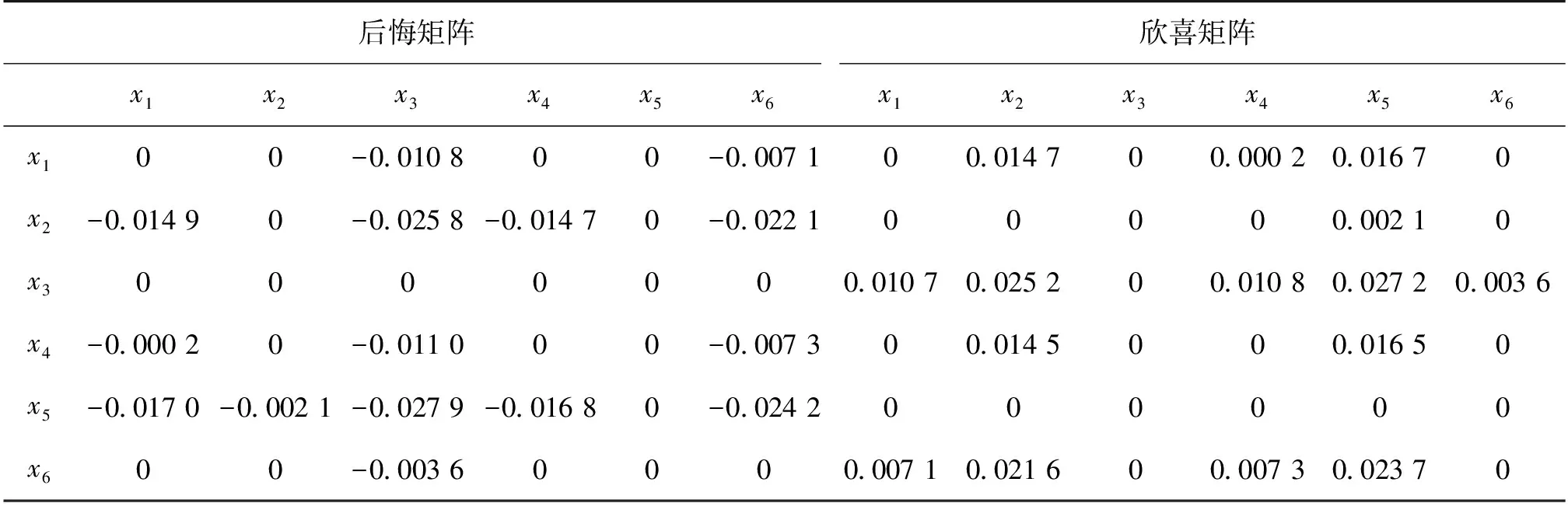


R(Ai)=(-0.067 6,-0.056 8,-0.045 3,-0.076 5,-0.033 5,-0.026 0)
Q(Ai)=(-0.282 5,-0.112 7,0.071 6,-0.400 0,0.207 8,0.600 0)4 结 论
