SDP全局误差界及其SDP广义弱尖锐性的刻画*

邹 林 洋

(重庆师范大学 数学科学学院，重庆 401331)

0 引 言

误差界在数学规划问题中有着广泛的研究。比如Robinson在文献[1]中建立了任意闭凸集在赋范空间中的全局误差界。Mangasarian在文献[2]中考虑了由有限多个可微凸不等式系统的闭凸集，并在Slater约束条件和渐近约束条件下建立了一个全局误差界。Klatter在文献[3]中研究了等式约束中扰动解的Hausdroff连续性和无扰动系统的全局误差界之间的关系。Deng在文献[4-5]中提出了在巴拿赫空间中假设剩余函数满足Slater约束的闭凸集误差界是成立的结论等。除此之外，(弱)尖锐性作为求解算法的一种重要工具吸引了一大批国内外优化界的专家学者对其进行研究。Luo等人[6]中对带锥约束优化问题定义了广义弱尖锐性以及证明了它在一定时间内是可以收敛的，广义弱尖锐性是研究算法的工具之一。

SDP作为特定的锥优化问题是重要的数学模型之一。SDP的约束系统等价于一个凸不等式系统，且凸不等式系统在凸规划的灵敏度分析和迭代算法收敛性分析中发挥着重要的作用。SDP的退化情形包括了线性规划和凸二次规划。SDP广泛地存在于系统与控制理论、金融工程、量子化学等诸多领域。SDP多项式内点算法为求解组合优化领域的某些中小规模的NP问题(如著名的旅行商问题)提供了有效的解决途径。自20世纪90年代初期至今，SDP 一直是优化领域的一个热门的研究问题。Deng和Hu在文献[7]中得到了SDP的误差结果和一个精确的SDP罚函数。因此，研究SDP的全局误差界和其广义弱尖锐性的关系，得到了一些新的结果。

第一部分介绍了主要用到的基本符号和定义，第二部主要定义SDP的广义弱尖锐性和凸系统下满足的度量正则性，给出了度量正则的一些性质。第三部分证明在一定条件下SDP的全局误差界和广义弱尖锐性之间的充分条件和必要条件。

1 预备知识

考虑半正定约束下的凸优化问题：

定义1 若存在一个常数c>0，使得对∀x∈X1有

(1)

成立，则称SDP的全局误差界成立。

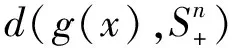
2 SDP广义弱尖锐性和度量正则性

基于文献[6]可知带锥约束的凸优化问题是具有广义弱尖锐性的，因为半正定锥是一个闭凸锥，因此半正定锥可以作为带锥约束凸优化的特例进一步研究它的广义弱尖锐性。首先定义SDP的广义弱尖锐性。

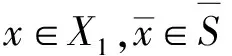
(2)

由于SDP的约束系统可以看作是一个凸不等式系统，因此先考虑凸不等式系统:

θ(x)≤0，x∈S

(3)

的一个全局误差界的结果。其中θ:Rn→R是一个连续的凸函数，集合S是SDP问题的可行集。

(4)

(5)

(6)

(b)⟹(c)：显然成立。

并且有：

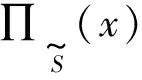
根据(c)的条件可得：

(7)

因为θ是一个连续凸函数，所以有：

(8)

将式(7)代入式(8)可得：

又[θ(x)]+=max{θ(x),0}，所以有：

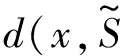
在SDP问题中，令

根据定理1，可以得到度量正则性与SDP广义弱尖锐极小性的关系。

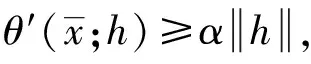
3 SDP全局误差界与广义弱尖锐性

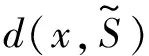
对∀x∈Rn则有：

(9)

推论2 在命题1的条件下，假设SDP的全局误差界成立，即满足

(10)

因为y∈X1，所以根据命题1条件可得：

将其代入式(10)得：

(11)

结合式(9)、式(11)得：

(12)

成立。

若Slater条件不成立，则对∀x∈X1，有函数θ(x)≥0；因此θ-1(0)是全局最小解集。

在度量正则的条件下得到一个关于SDP全局误差界和其广义若尖锐性的一个充分必要条件。

(13)

成立。所以有：

(14)

由式(13)、式(14)可得：

将上式与式(13)联立可得：

所以由定义1知结论成立。