有限长圆柱绕流气动噪声源特性分析

杨志刚，刘洋，王毅刚



有限长圆柱绕流气动噪声源特性分析

杨志刚1,2，刘洋1，王毅刚1

(1. 同济大学上海地面交通工具中心，上海 201804；2. 北京民用飞机技术研究中心，北京 102211)

气动噪声源的能级、分布特性及其产生根源还不够清晰。以有限长三维圆柱绕流为研究对象，基于声源方程分析气动噪声源的种类构成及其与气动参数的关系，通过数值计算得到可压非定常流场，利用气动参数定量计算圆柱顶部、中部和底部的声源大小分布，研究声源的分布特性和产生根源。结果表明，在有限长圆柱绕流场中，以偶极子声源为主，单极子声源可以忽略不计，四极子源项的值比偶极子小1～2个数量级。偶极子主要分布在来流分离点及圆柱后壁面湍流涡二次碰撞区域，四极子主要分布在来流分离点及其向后拖曳区域。偶极子声源主要由于圆柱两侧涡脱落处的脉动压力在横向(y方向)上的二阶梯度引起。以上结果为气动噪声控制的进一步研究提供了借鉴和参考。

气动噪声；有限长圆柱；声源方程；偶极子源

0 引言

气动声学是指研究流体自身及流体与固体边界相互作用发声机理的一门学科[1]，气动噪声广泛存在于航空、高速列车及汽车等领域，研究气动噪声具有重要的实际意义，探讨、分析气动噪声源特性，是控制气动噪声至关重要的关键之一。Lighthill[2-3]提出了声类比理论，并没有考虑流动中可能存在的固壁影响，只适用于自由空间，所以Lighthill方程右侧项只有四极子。Curle[4]运用基尔霍夫积分公式改进了Lighthill声类比理论，考虑了静止固体壁面对流动发声的影响，固壁的影响相当于在固壁表面分布有一层偶极子源，所以方程右侧的源项为偶极子和四极子的叠加。Ffowcs Williams等[5]应用广义函数法将Curle的结果扩展到考虑运动固体边界对声音的影响，即物体在流体中运动的发声问题，提出Ffowcs Williams-Hawkings方程(FW-H方程)。从FW-H方程可以看出，运动物体与流体相互作用产生的声场是由四极子源、偶极子源以及由于质量移动效应所产生的单极子源的叠加组成的。Howe[6-7]简化了Lighthill方程，得到了适用于低马赫数、高雷诺数的流场的Howe方程，方程的右端项表明流场中的漩涡可以作为声源。

关于圆柱绕流气动噪声的数值计算方法和噪声特性分析的相关研究已经比较广泛，而对于圆柱绕流气动噪声源的研究比较缺乏，尤其是三维气动噪声源的研究。Cox等[8-9]通过雷诺时均法(Reynolds Average Navier-Stokes, RANS)计算二维非定常圆柱绕流，并基于FW-H方程计算了偶极子源和四极子源，发现四极子源对总噪声的贡献相对于偶极子源可以忽略。Takaishi等[10]通过大涡模拟得到瞬态流场特征，运用广义格林公式准确预测了偶极子声源在高速列车转向架区域的分布。A. Iida等[11]通过广义格林公式和相干输出功率(Coherent Output Power, COP)两种方法预测了偶极子声源的分布，两种方法的结果吻合得很好，结果显示偶极子声源是在卡门涡街形成区域附近产生的，分离的剪切层对偶极子声源有着重要的作用。郑朝荣等[12]采用可实现-湍流模型和宽频带噪声源模型相结合的方法研究钝体绕流的气动噪声源，结果表明钝体绕流气动噪声主要分布在来流分离和湍流运动比较剧烈的位置，四极子源项的值相对于偶极子源项小很多。

从上述的研究文献中发现，对于三种声源的具体数量级大小、分布还需要深入研究，声源的产生根源也不是很清楚。本文以有限长圆柱绕流为例，通过数值计算定量研究单极子、偶极子和四极子声源的具体大小和分布特性，并分析了声源的产生根源。

1 气动噪声理论

1.1 基尔霍夫定理

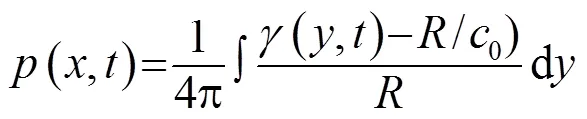
当反射、吸收甚至发射声波的固体边界存在时，我们假设存在一个包围源和固体边界的假想面，观测点在表面的外部，如图1所示，推导得

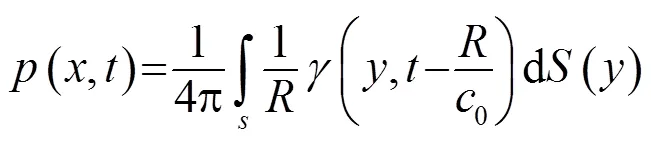
该结果称为基尔霍夫定理[13]。Curle运用这一定理将Lighthill定理推广到静止固壁存在情况下声场的求解，并应用到后续的FW-H方程中。此后在流体噪声和气动噪声的各种推广应用中，有关声场的解均基于基尔霍夫积分公式。

1.2 声源方程及声源项的确定

由静止介质中的连续方程和动量方程，可得声波方程：

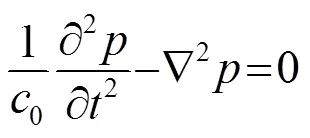
声波方程描述了声波在静止介质中的传播，但是不包含任何有关声源的信息。现在假定在域中有质量源，单位为kg·m-3，则连续性方程为

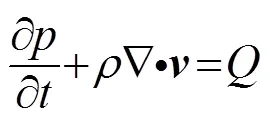
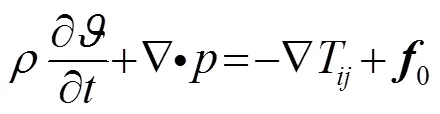
将式(4)对微分，将式(5)对微分，然后两式相减得

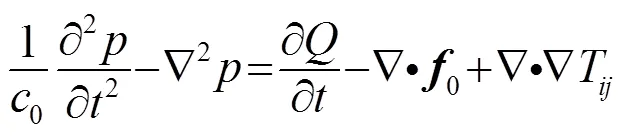
该式为声源的通用方程[14]。方程的左边为传播项，方程的右边三项依次为单极子声源、偶极子声源和四极子声源。

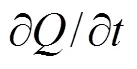
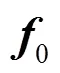
式(7)的物理意义为力点源可能由于压力梯度产生，也可能由于速度的旋度产生，或者是两者的组合。故偶极子声源为

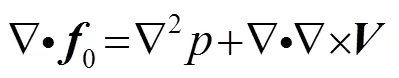
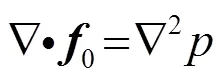
四极子声源是由于物体周围紊流流体内的应力变化产生的，本质上是一种流体湍流应力源。-方程(动量方程)为

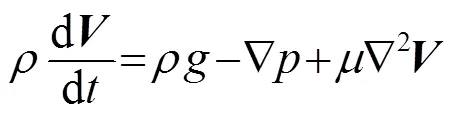
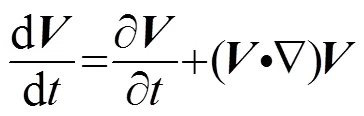
将式(10)代入式(9)，得：

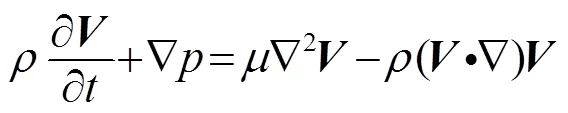
式(11)与连续性方程联立，解得

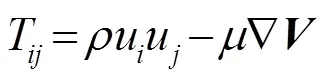
故四极子源项为

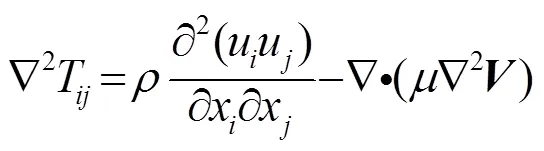
2 圆柱绕流数值计算

2.1 数值计算方法

以气动-声学风洞试验的圆柱绕流模型为研究对象，如图2所示，圆柱直径=0.1 m，高度和直径之比为18.5：1，高=1.85 m，在圆柱顶部有和试验模型一致的半球，使圆柱顶部流动分离不过于剧烈，圆柱底部有一个锥度很小的底座，使圆柱固定更加稳定。流场计算区域示意图如图1所示，以圆柱底部中心点为坐标原点，流向长度取为-10～25，横向为-8～8，展向为0～28。声源区为如图所示的矩形区域，尺寸为8.2×4×20，声源区前端距圆柱轴线1.2，后端距圆柱轴线7，基本包含了圆柱绕流涡脱落影响的核心区域。

计算域分块划分六面体网格，用O-Grid型网格划分圆柱的边界层和加密区，网格在圆柱近壁面沿周向等分，径向在近壁面密布边界层，大涡模拟通常要求+(第一层网格质心到壁面的无量纲距离)值小于1，+也可以增加到5[15]，由于计算资源的限制，本次计算+取2，第一层边界层厚度为0.018 mm，增长率为1.05，边界层一共39层。声源区最大网格尺寸为10 mm，最终网格总数约为4 086万。

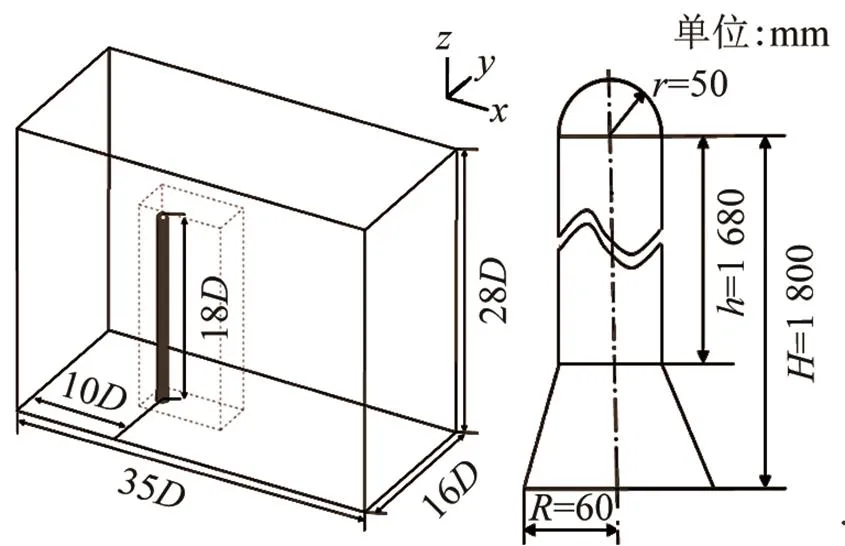
图2 圆柱绕流模型图

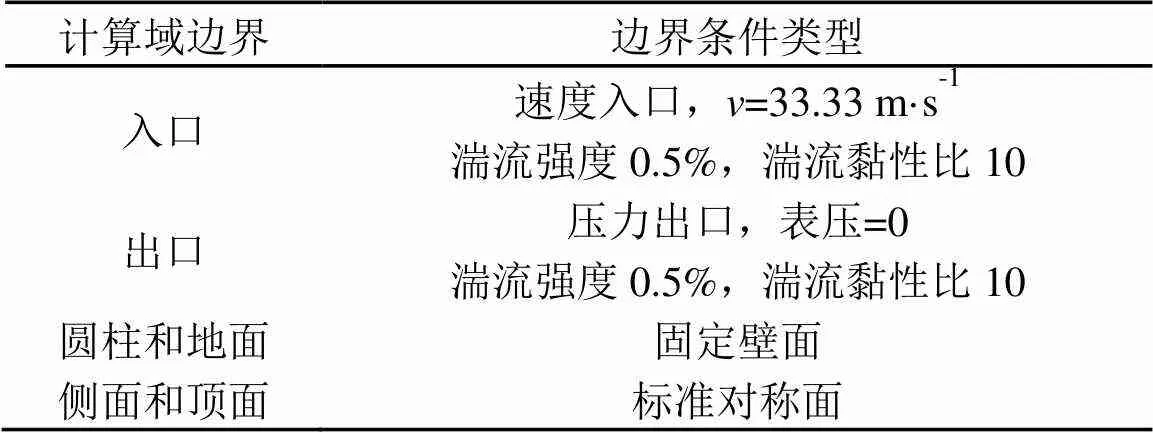
表1 定常流动计算的边界条件设置

2.2 气动噪声数值计算及风洞试验

气动噪声数值计算也是在Fluent的非定常流场中进行，采用Ffowcs Williams-Hawkings(FW-H)声学模型，并设置选取声源区，将大涡模拟非定常流动计算中获得的流动参数，如压力和速度等，代入FW-H方程的声源项中，通过对远场的积分，得到远场接收点的声压数据。

为了验证上述圆柱绕流仿真计算的正确性及气动噪声控制措施，本文开展了风洞实验研究。试验在同济大学上海地面交通风洞中心的整车气动-声学风洞中进行。试验用圆柱为实心钢圆柱，顶部设计成一个半球结构以避免强的气动噪声产生，其根部采用圆台结构(增大其与地面的接触面积)固定于试验段的地面上，以保证圆柱在较高风速下不晃动。圆柱直径为0.1 m，高为1.85 m。图3标明了试验圆柱在风洞中的具体位置和远场传声器测点位置。3个传声器轴线距圆柱5 m，传声器间距1.3 m，高为1.2 m。传声器为丹麦GRAS公司的产品，数据采集及分析系统为HEAD公司的产品。试验内容包括光滑圆柱气动噪声试验和覆盖多孔介质圆柱气动噪声试验。试验风速为120 km·h-1。

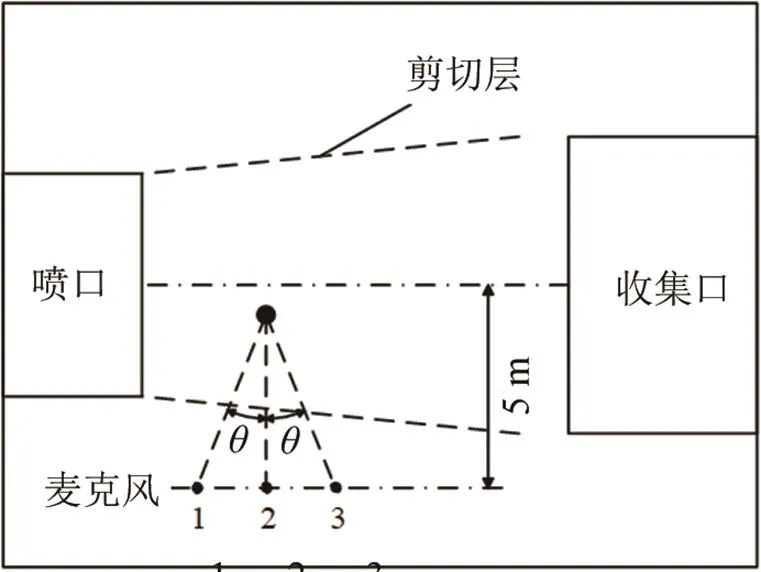
图3 圆柱和麦克风位置俯视图

图4为风速为120 km·h-1下，距圆柱5 m远处传声器测量和仿真计算的A计权频谱。从图4中的测量结果可以看出，在64 Hz附近出现了明显峰值，声压级为78.18 dB，是圆柱典型的涡脱落引起的。由于圆柱顶部和地面影响，在峰值附近出现较低的另外峰值并有一定的带宽，但并没有掩盖绕流圆柱涡脱落的峰值特征。从仿真结果可以看出，在67 Hz附近出现明显峰值，声压级为72.74 dB。本圆柱涡脱落频率为66.67 Hz，测量结果和仿真结果都接近该值，峰值声压级相差5.44 dB，表明仿真结果和试验结果两者峰值频率和大小基本一致，说明了仿真计算的正确性。

图4 仿真和实测的远场噪声频谱图

3 圆柱绕流数值计算结果分析

3.1 气动噪声源分布特性

气动噪声源的分布特性与流场各项气动参数有关，对于有限长度的圆柱，圆柱顶部、中部和根部的流态不尽相同，需要分别加以分析。

对于圆柱顶部，选取=0截面进行分析。图5为=0截面圆柱顶部的单极子分布图，单极子源项的数量级为0～10，数量级很小，可以忽略不计。

图5 圆柱顶部单极子分布

图6为=0截面圆柱顶部的偶极子分布图。在圆柱顶部-90°～27°，偶极子紧贴圆柱顶部分布，且分布区域逐渐变厚；在27°位置处，偶极子的分布区域开始从圆柱表面分离，形成一个拖曳区域；在90°位置处也存在一个小的分离，同时形成一个小的拖曳区域；在圆柱截面来流后壁面1.63～1.76 m处，存在一个贴着壁面分布的偶极子区域，厚度约为10 mm。圆柱顶部偶极子的最大值数量级为109～1010。

图7为=0截面圆柱顶部的四极子分布图，在圆柱顶部-90°～0°，紧贴圆柱表面分布着一层很薄的四极子；从0°～43°四极子区域逐渐变厚，并在43°处开始从圆柱表面分离，产生一个较大的拖曳区域；在圆柱截面来流后壁面1.62～1.80 m处，存在一个分布较为广泛的四极子区域，在1.68～1.77 m处，四极子的分布范围更加向后拉长，长度约为85 mm。圆柱顶部四极子的最大值数量级为108～109。

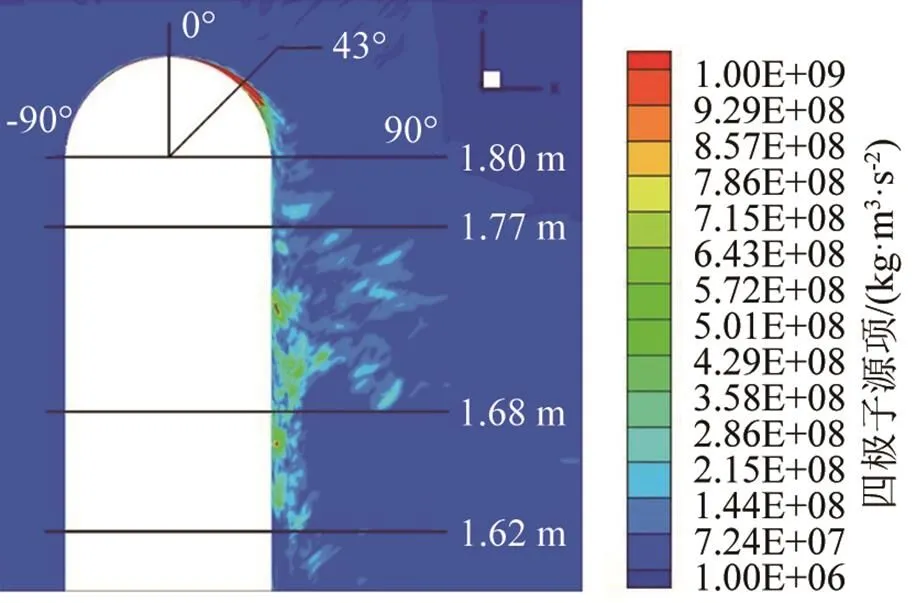
图7 圆柱顶部四极子分布

对于圆柱中部，分别选取=0.8、1.0、1.2 m处的横截面加以分析。图8显示了圆柱在=0.8、1.0、1.2 m处横截面上单极子声源在圆柱绕流场中的大小分布情况，单极子主要分布在圆柱分离点附近及尾涡区域，并且圆柱来流侧的单极子较大。单极子源项的值分布在0～10左右，数量级很小，可以忽略不计。

图9依次显示的是圆柱=0.8、1.0、1.2 m处横截面上偶极子声源在圆柱绕流场中的大小分布情况。在圆柱中部三个不同高度截面的偶极子分布情况基本相同，且左右基本对称。从0°～100°附近，紧贴圆柱表面存在一层较薄的偶极子区域，随着角度的增大，偶极子区域逐渐变厚；在100°附近偶极子分布区域开始从圆柱表面脱离，并向后形成一个短小的拖曳区域；在100°～180°区域，紧贴圆柱壁面形成一层较薄且不连续的偶极子分布区域。圆柱中部偶极子的最大值数量级为109～1010。

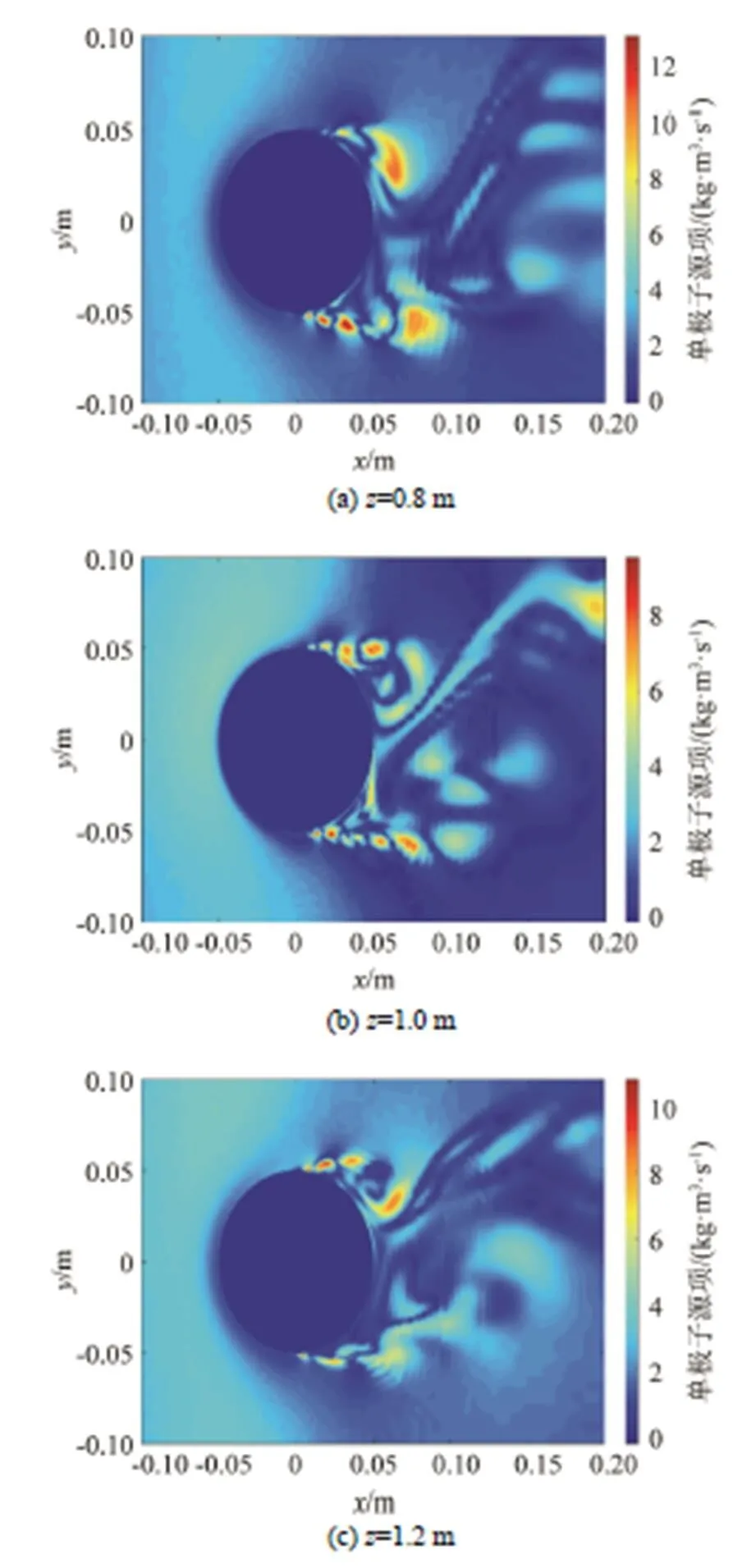
图8 圆柱中部单极子分布

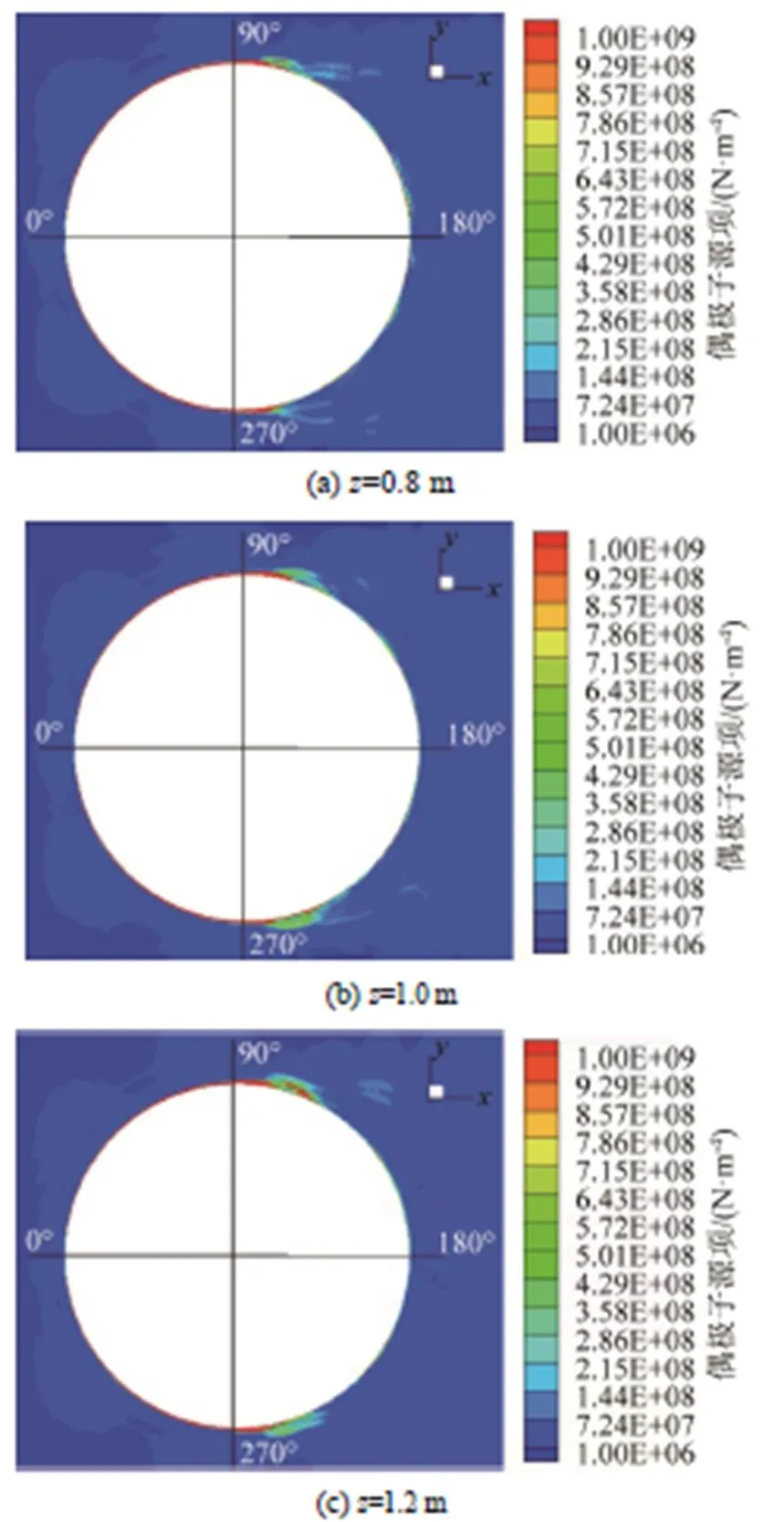
图9 圆柱中部偶极子分布

图10分别显示的是圆柱=0.8、1.0、1.2 m处横截面上四极子声源在圆柱绕流场中的大小分布情况。圆柱中部三个不同高度截面的四极子分布基本相同，且左右基本对称。在0°～98°紧贴圆柱壁面分布有一层较薄的四极子，在0°和90°附近的四极子相对较薄、较少；在98°～142°区域形成一个比偶极子分布区域更宽更长的四极子分布区域；在142°～180°圆柱表面和后面分布有一些值较小且杂乱的四极子区域。圆柱中部四极子的最大值数量级为108～109。

经过上述分析，在圆柱中部偶极子的强度最大，单极子比偶极子小7～8个数量级，四极子比偶极子小1个数量级。为了更具体地对比圆柱中部偶极子和四极子的大小分布情况，在=1.0 m的横截面上取=0、25、50、75 mm，从-100～300 mm每隔10 mm取一个点，圆柱区域内的点除外，如图11所示。对比每个点上偶极子和四极子源项的值，如图12～15所示。

由图12～15可知，在=1.0 m截面上紧贴圆柱表面0°和180°处，偶极子源项的值比四极子大1～2个数量级，在圆柱两侧的涡脱落区域从-10～20 mm的范围内，偶极子比四极子大1～2个数量级，在其他区域，偶极子和四极子大小基本相同。

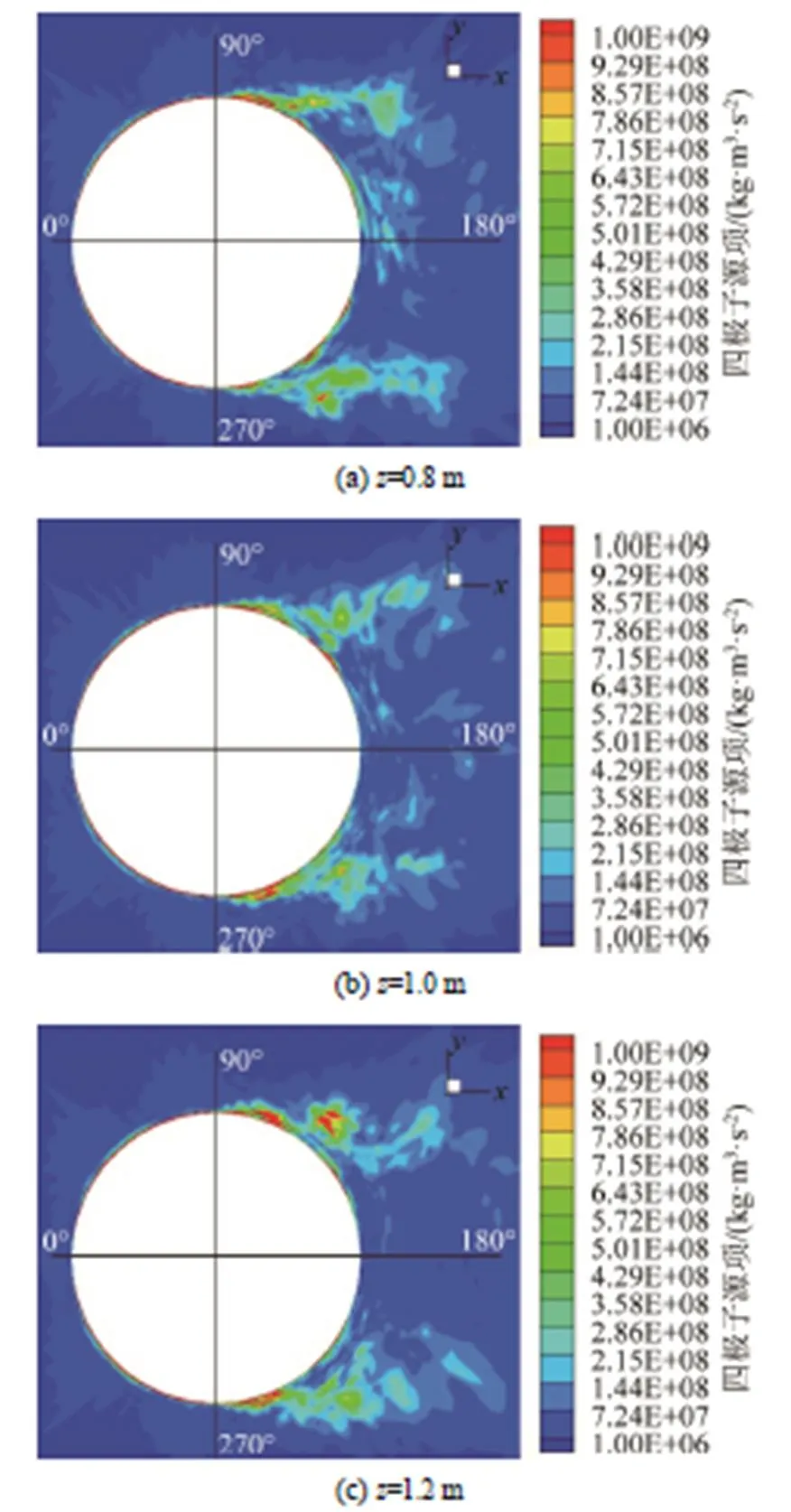
图10 圆柱中部四极子分布

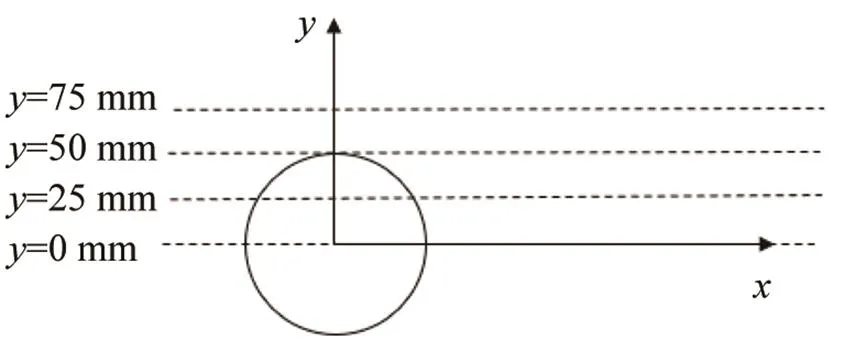
图11 圆柱中部z=1 m截面测点分布

对于圆柱底部，分别选取=0截面和=60 mm截面进行观察分析。图16为圆柱底部单极子的大小分布图，单极子量级为0～10，可以忽略不计。图17、18分别为圆柱底部偶极子和四极子的大小分布图，在=60 mm截面处的偶极子和四极子分布与圆柱中部截面分布类似，从=0 mm截面观察，圆柱底部偶极子和四极子分布与圆柱中部也并没有什么不同。因此，圆柱底部的偶极子、四极子分布特性与圆柱中部的偶极子、四极子分布特性相同。

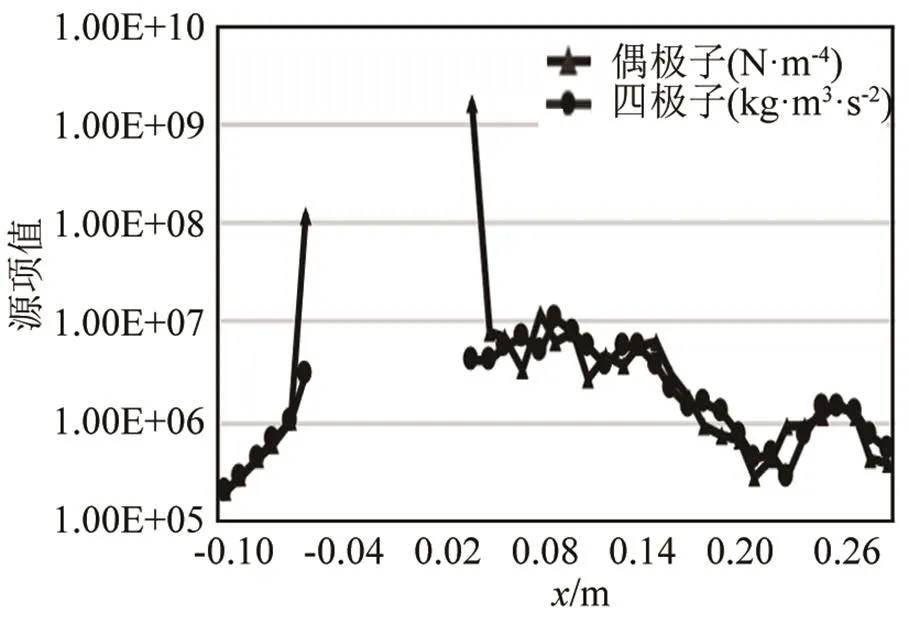
图12 y=0 mm测点的偶极子和四极子大小分布

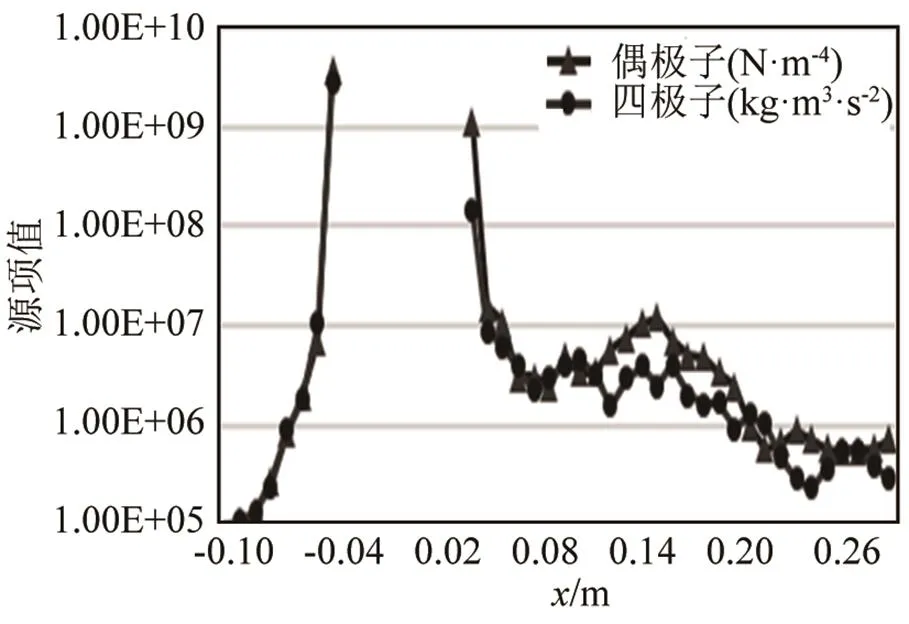
图13 y=25 mm测点的偶极子和四极子大小分布

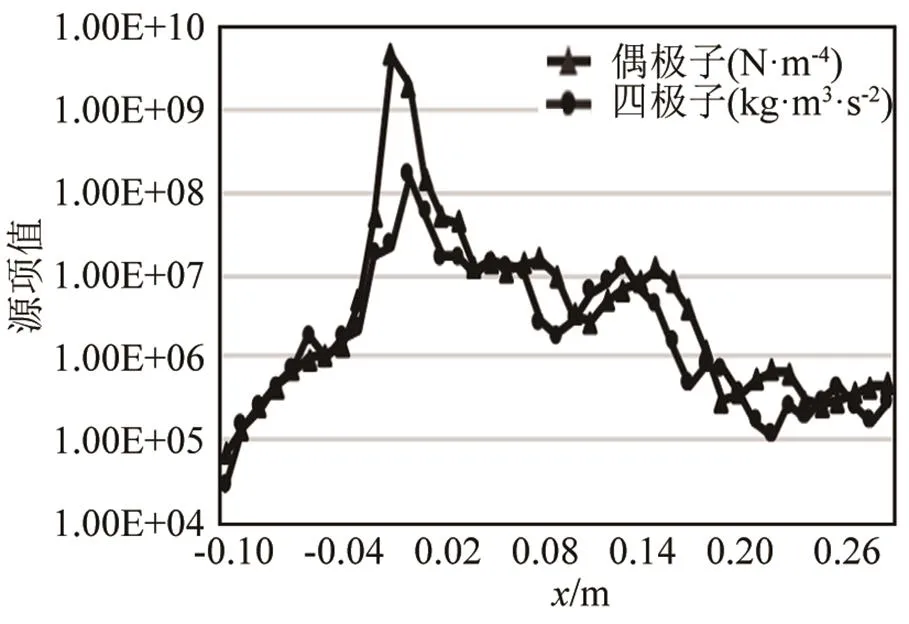
图14 y=50 mm测点的偶极子和四极子大小分布

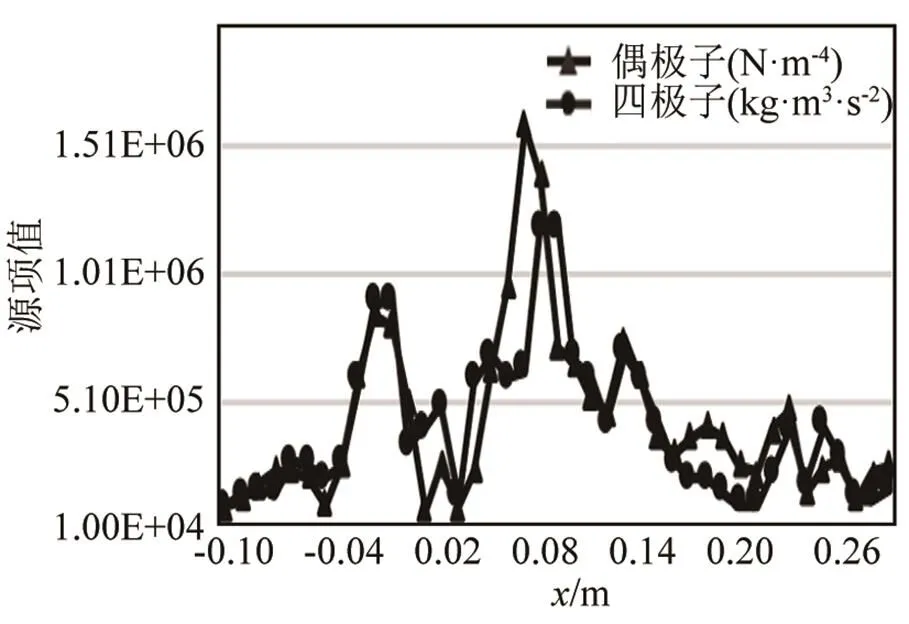
图15 y=75 mm测点的偶极子和四极子大小分布

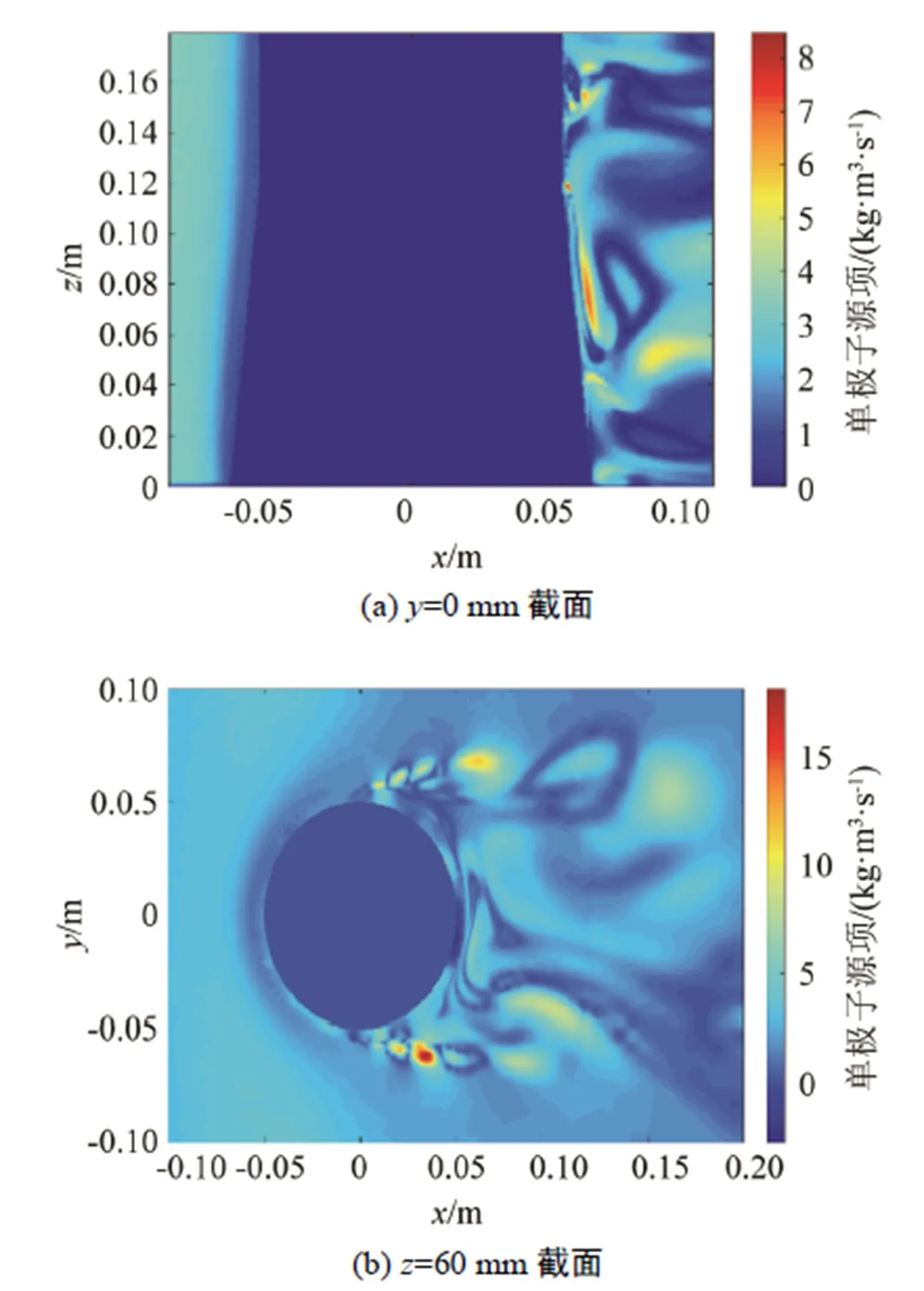
图16 圆柱底部单极子大小分布

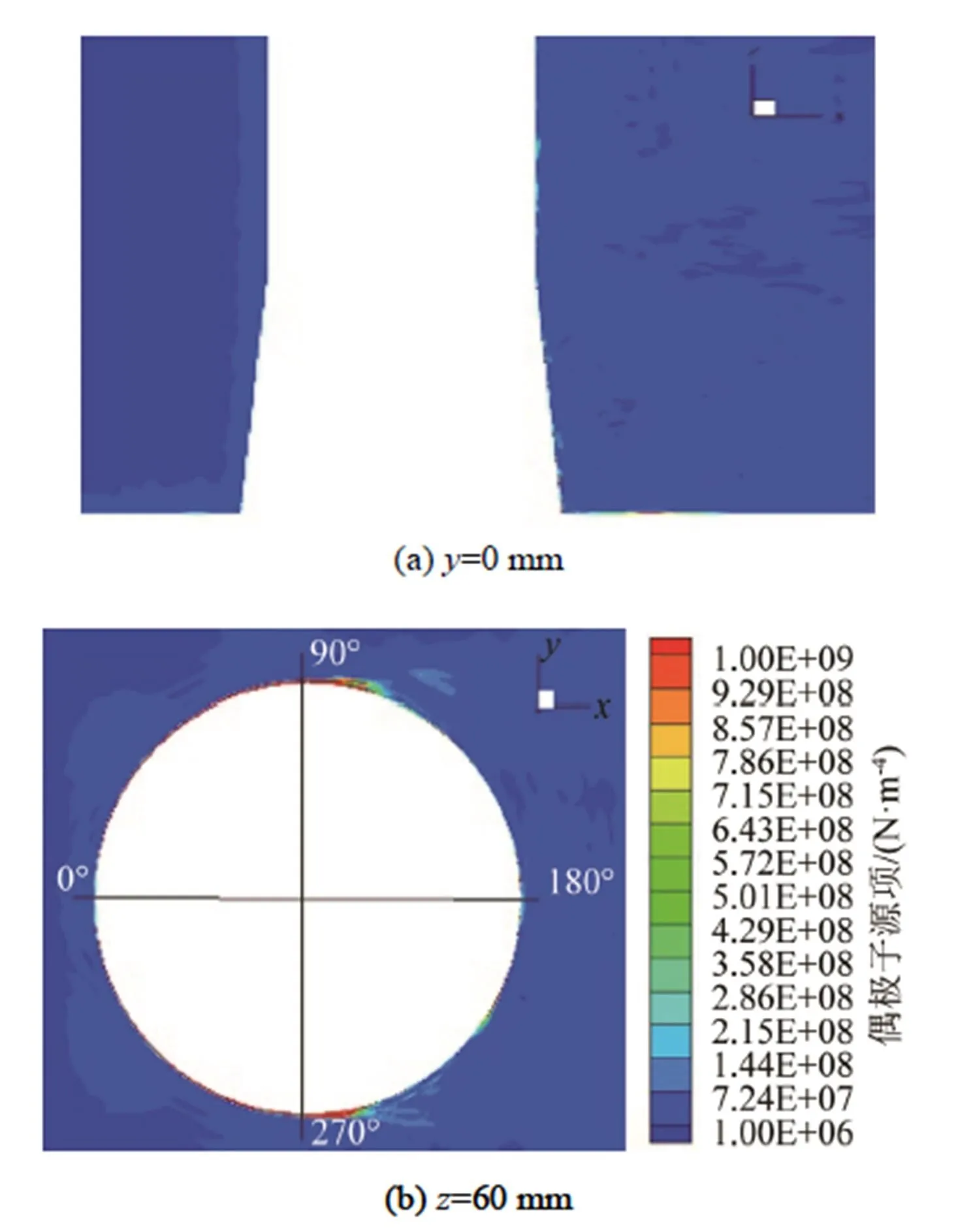
图17 圆柱底部偶极子大小分布

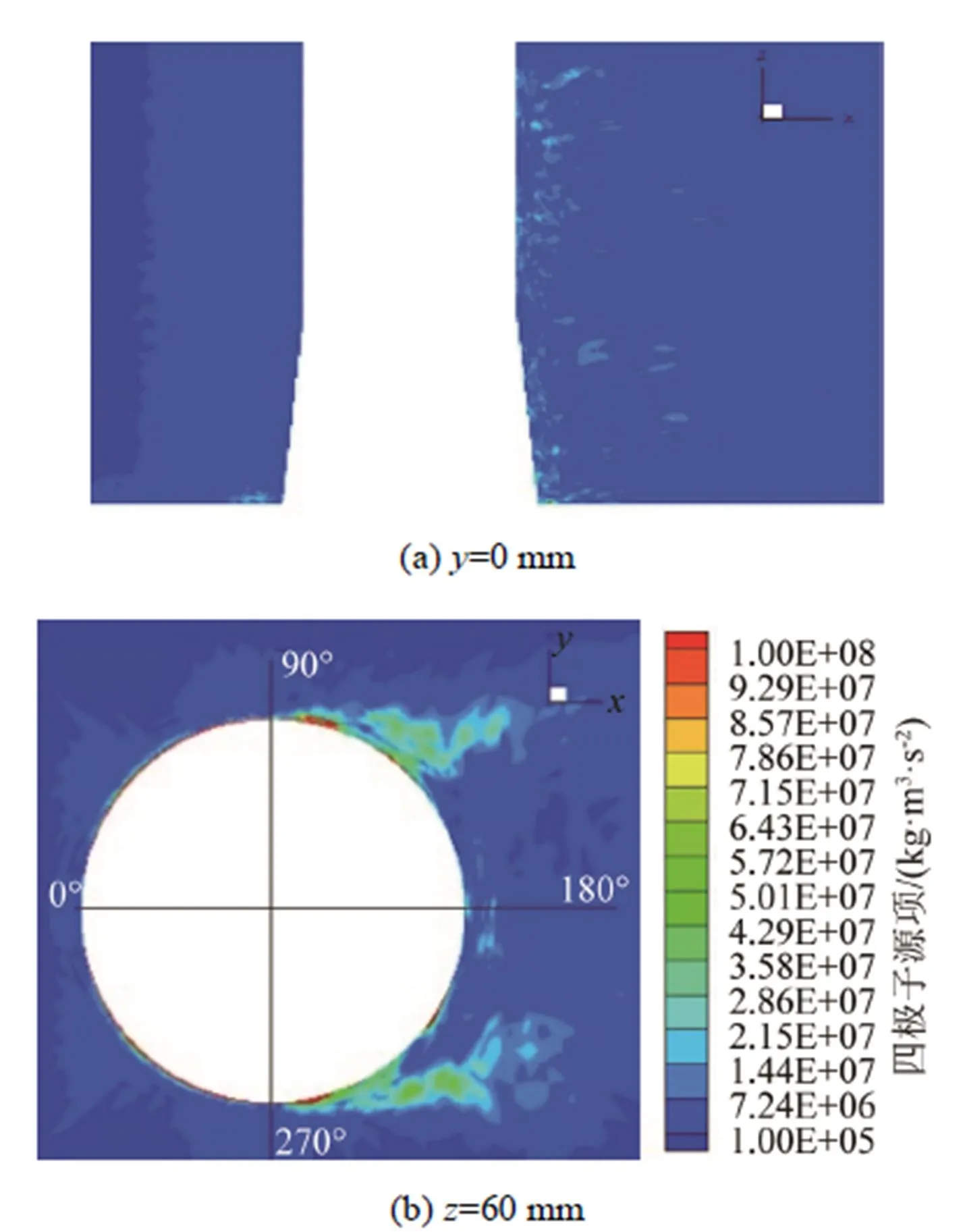
图18 圆柱底部四极子大小分布

3.2 偶极子源分析

偶极子是圆柱绕流的主要声源，需要对偶极子的分布特征和产生根源做进一步探究。图19为圆柱顶部速度流线图，偶极子声源是由于圆柱对其边界上的流体的作用力产生的，在圆柱顶部-90°～27°范围内，来流与圆柱表面相互作用，产生一个紧贴圆柱顶部表面的偶极子区域；接着气流涡向下回旋，与圆柱后壁面1.63～1.76 m范围发生碰撞作用，故该区域分布有一层不连续且较厚的偶极子区域。

图20为=1.7 m截面处的流线图，来流经过圆柱顶部向下形成湍流涡，二次碰撞圆柱后壁，形成偶极子区域。

图21为=1.0 m处横截面上的速度流线图，在速度流线图中可以明显地看到，在圆柱表面0°～100°范围，来流与圆柱表面碰撞产生作用力，故存在一层紧贴圆柱表面的偶极子区域；在圆柱后侧100°～180°范围，气流涡二次碰撞圆柱后壁，故产生一层紧贴圆柱后壁的不连续的偶极子区域。

在有限长圆柱绕流中，偶极子作为主要噪声源。在声源方程中，偶极子表示为

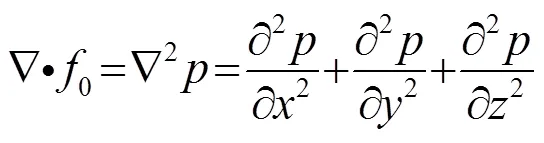
偶极子源由脉动压力在x、y、z三个方向的二阶梯度构成，为了进一步分析产生偶极子的根源，分别计算脉动压力在x、y、z三个方向的二阶梯度，进行比较分析。图22为z=1.0 m截面上的脉动压力云图，脉动压力在圆柱两侧的来流分离点附近及其向后形成的拖曳区域沿y方向变化比较明显。图23依次为z=1.0 m截面上dp/dx、dp/dy和dp/dz的云图，dp/dy的值大于dp/dx和dp/dz，且主要分布在圆柱两侧的来流分离点附近及其向后形成的拖曳区域。图24依次为z=1.0 m截面上d2p/dx2、d2p/dy2和d2p/dz2的云图，d2p/dy2的云图与图9中z=1.0 m 截面上的偶极子分布图基本相同；d2p/dx2主要分布在紧贴圆柱的来流侧，紧贴圆柱后侧表面也分布有一层不连续的区域，且分布区域很薄；d2p/dz2的值相对于d2p/dx2和d2p/dy2较小，对∇2p影响不显著。因此，∇∙f0主要来源于d2p/dy2，偶极子主要由来流分离处的脉动压力沿y方向的二阶梯度引起。

图20 z=1.7 m截面流线图

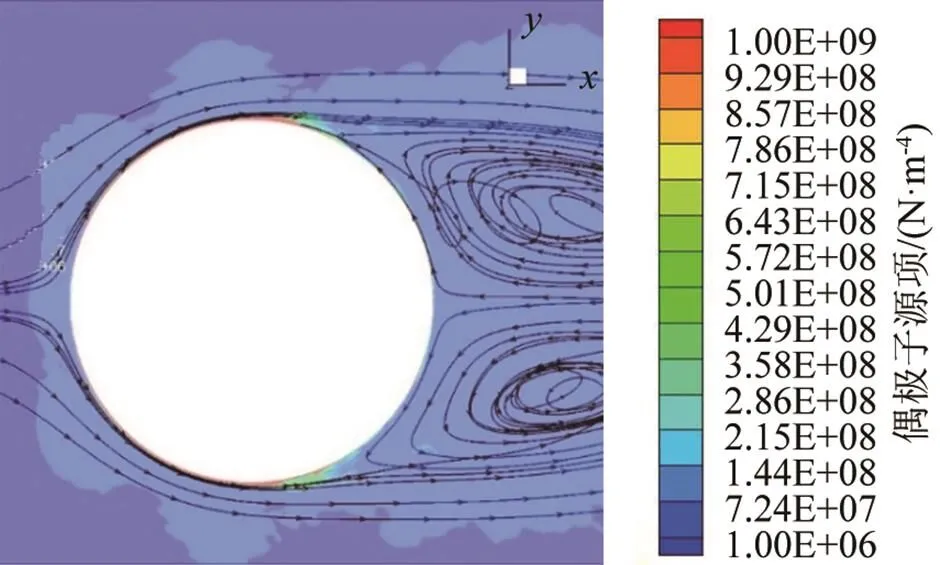
图21 z=1.0 m截面流线图

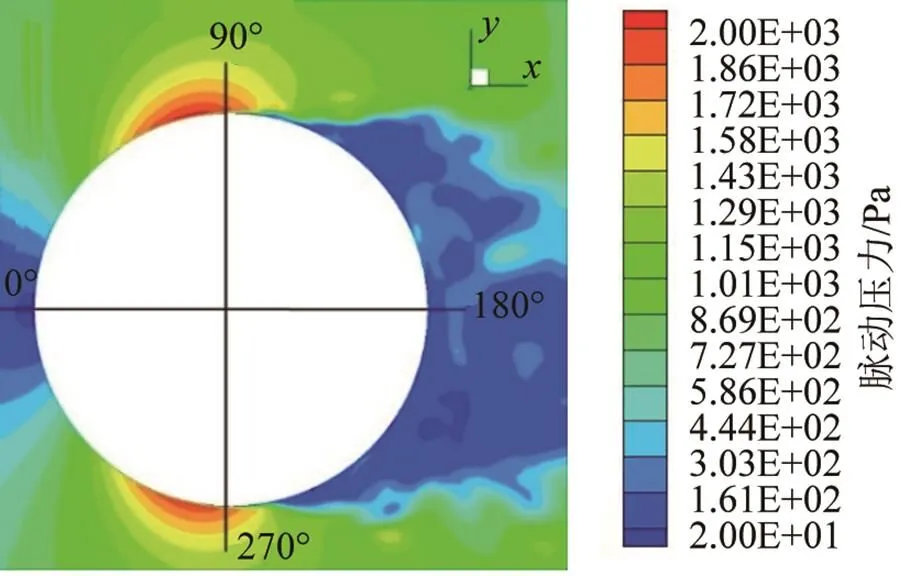
图22 圆柱体z=1.0 m截面上的脉动压力云图

3.3 四极子源分析

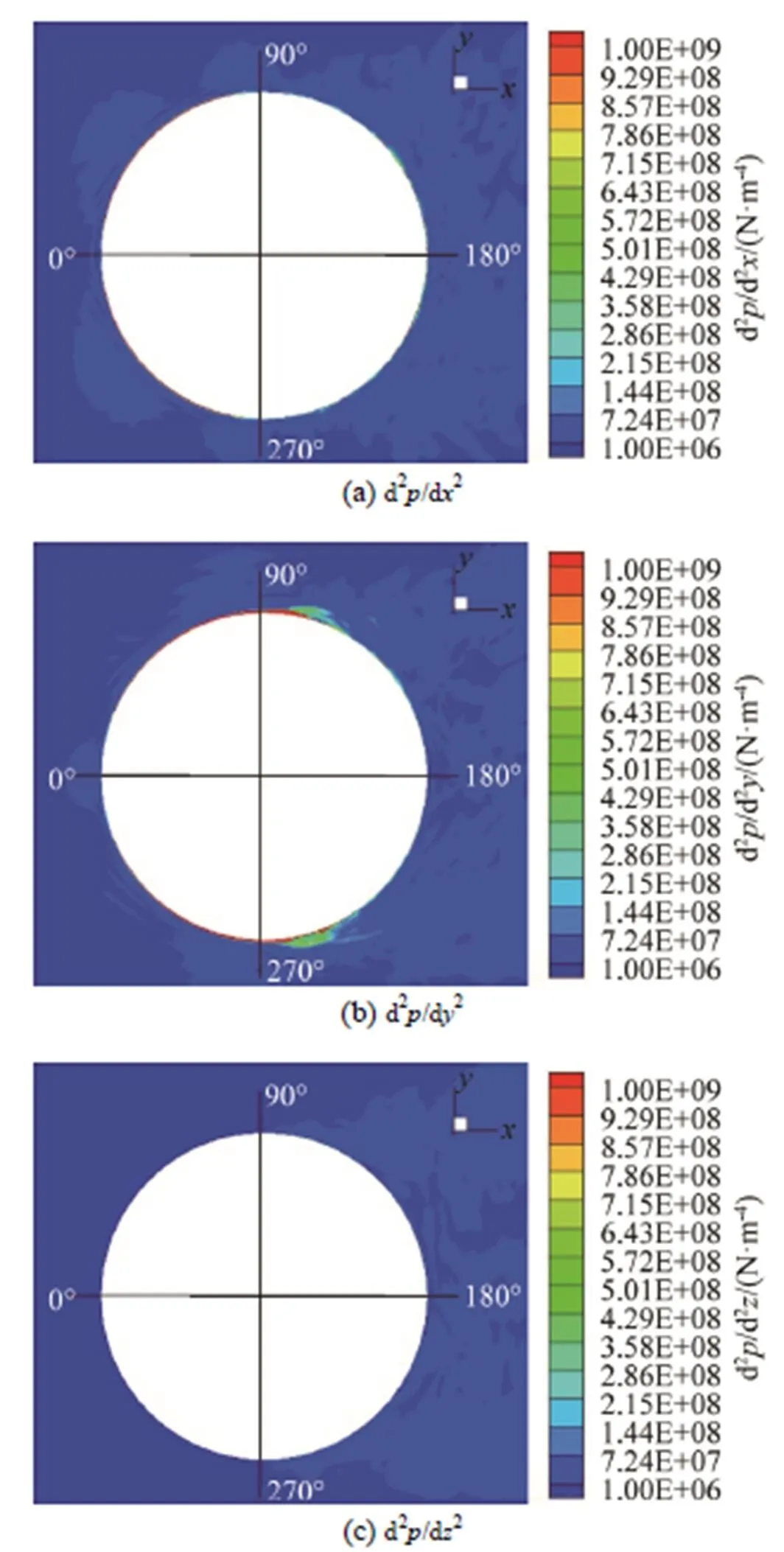
图24 圆柱体z=1.0 m截面上的d2p/dy2、d2p/dy2、d2p/dy2云图

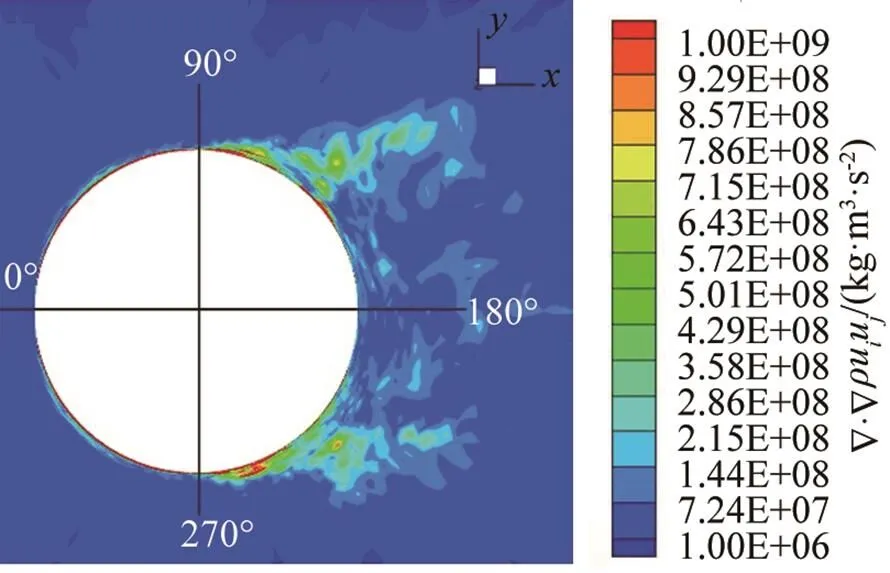
图25 圆柱体z=1.0 m截面上的分布情况

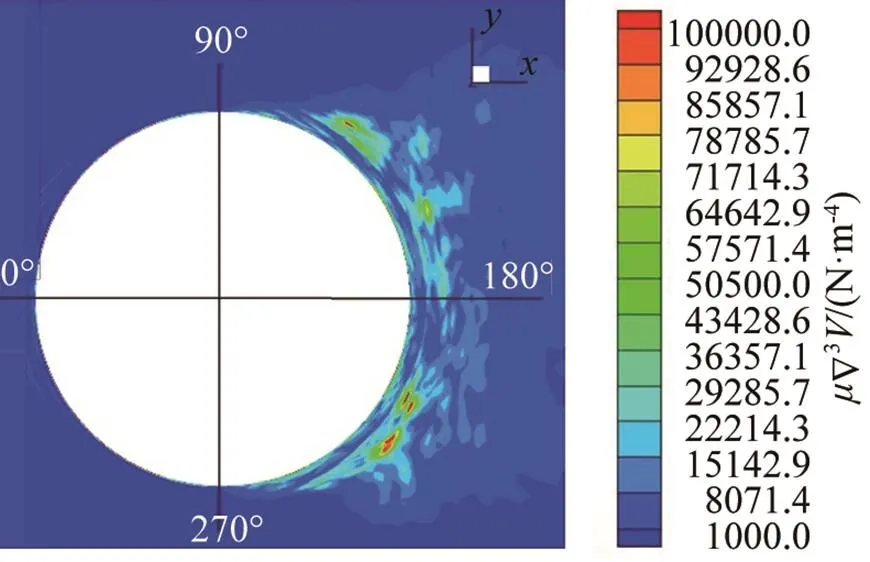
图26 圆柱体z=1.0 m截面上的分布情况

4 结论

本文通过大涡模拟计算得到三维可压非定常圆柱绕流场，基于声源方程从新的角度定量分析圆柱绕流场中单极子、偶极子和四极子声源的分布特性，更加清晰地认识到声源的产生根源，为气动噪声的控制提供了理论依据。得到的主要结论如下：

(1) 通过大涡模拟和FW-H方程得到的远场噪声与风洞试验结果比较吻合。表明大涡模拟得到的圆柱绕流可压非定常流场可以为气动噪声源的计算提供可靠的声源信息。

(2) 对于有限长圆柱，偶极子气动噪声源占主导地位，单极子源项的值比偶极子低8～9个数量级，四极子源项的值比偶极子低1个数量级左右。

(3) 偶极子源主要分布在圆柱顶部27°来流分离点附近和圆柱中部、底部两侧的分离点附近及圆柱来流侧表面，偶极子源主要由脉动压力沿方向的二阶导数d2/d2产生。

(5) 由于计算过程中运用的声源方程右侧源项仅表征了源项的幅值大小，并未考虑声传播及声源辐射效率。关于不同声源对接收点处总声场的贡献率有待进一步研究。

[1] 孙晓峰, 周盛. 气动声学[M]. 北京: 国防工业出版社, 1994.

[2] LIGHTHILL M J. On sound generated aerodynamically. i. general theory[J]. Proceedings of the Royal Society of London, 1952, 211(1107): 564-587.

[3] LIGHTHILL M J. On sound generated aerodynamically. II. Turbulence as a source of sound[J]. Proceedings of the Royal Society of London. Series A. Mathematical and Physical Sciences, 1954, 222(1148): 1-32.

[4] CURLE N．The Influence of solid boundaries upon aerodynamic sound[C]//Proceedings of the Royal Society of London, 1955, Series A(231): 506-514.

[5] WILLIAMS J E F, HAWKINGS D L. Sound generation by turbulence and surfaces in arbitrary motion[J]. Philosophical Transactions of the Royal Society of London. Series A, Mathematical and Physical Sciences, 1969, 264(1151): 321-342.

[6] HOWE M S. Edge, cavity and aperture tones at very low mach numbers[J]. J. Fluid. Mech, 1997, 330(4): 61-84.

[7] HOWE M S. Acoustics of fluid-structure interactions[M]. Cambridge University Press, 1998.

[8] COX J S, BRENTNER K S, RUMSEY C L. Computation of vortex shedding and radiated sound for a circular cylinder: subcritical to transcritical reynolds numbers[J]. Theoretical & Computational Fluid Dynamics, 1998, 12(4): 233-253.

[9] BRENTNER K S, COX J S, RUMSEY C L, et al. Computation of sound generated by flow over a circular cylinder: an acoustic analogy approach[C]//Computational Aeroacoustics Workshop on Benchmark Problems NASA. 1997: 1-9.

[10] TAKAISHI T, SAGAWA A, NAGAKURA K, et al. Numerical analysis of dipole sound source around high speed trains[J]. J. Acoust. Soc. Am., 2002, 111(6): 2601-2608.

[11] IIDA A, MIZUNO A, KATO C. Visualization of aerodynamic sound source with compact green's function[C]//Aiaa/ceas Aeroacoustics Conference & Exhibit. 2002.

[12] 郑朝荣, 王笑寒, 武岳. 钝体绕流气动噪声源特性数值研究[J]. 哈尔滨工业大学学报, 2017, 49(12): 146-151.

ZHENG Chaorong, WANG Xiaohan, WU Yue. Numerical investigation on the characteristics of aerodynamic noise sources induced by flows around bluff bodies[J]. Journal of Harbin Institute of Technology, 2017, 49(12): 146-151.

[13] [美]戈德斯坦. 气动声学[M]. 闫再友译. 北京: 国防工业出版社, 2014.

[America]Goldstein. Aeroacoustics[M]. RAN Zaiyou translate. Beijing: National Defense Industry Press, 2014.

[14] 唐狄毅, 李文兰, 乔渭阳. 飞机噪声基础[M]. 西安: 西北工业大学出版社, 1995.

TANG Diyi, LI Wenlan, QIAO Weiyang. Aircraft Noise[M]. Xi’an: Northwestern Polytechnical University Press, 1995.

[15] LEE A H, CAMPBELL R L, HAMBRIC S A. Coupled delayed-detached-eddy simulation and structural vibration of a selt-oscillating cylinder due to vortex-shedding[J]. Journal of Fluids and Structural, 2014, 48(7): 216-234.

[16] 蔡建程, 潘杰, 鄂世举, 等. 圆柱绕流气动声的偶极子及四极子源法定量研究[J]. 声学学报, 2016, 41(3): 420-427.

CAI Jiancheng, PAN Jie, E Shiju, et al.Quantitive study of the aerodynamic sound induced by the flow past a cylinder based on dipole and quadrupole m odels[J]. Acta Acustica, 2016, 41(3): 420-427.

Study of aeroacoustic noise source induced by a cylindrical flow offinite length

YANG Zhi-gang1,2, LIU Yang1, WANG Yi-gang2

(1. Tongji University, Shanghai Automotive Wind Tunnel Center, Shanghai 201804, China; 2. Beijing Aeronautical Science & Technology Research Institute, Beijing 102211, China)

The energy level, distribution characteristics and origin of aerodynamic noise source are not clear enough. The three-dimensional flow around a finite-length cylinder is taken as the research object. Based on acoustic source equations, the types of aerodynamic noise sources and their relationship with aerodynamic parameters are analyzed. Compressible unsteady flow is calculated numerically and then the aerodynamic parameters are used to quantitatively calculate the sound sources distribution at the top, middle and bottom of the cylinder in order to study the distribution characteristics and origin of the sound sources. Results show that the dipole sound source is dominant in the flow field and the monopole sound source is negligible, the quadrupole sound source is 1-2 orders of magnitude smaller than the dipole sound source, the dipole are mainly distributed at the separation points of incoming flow and the secondary collision zone of eddy flow on the back of cylinder, and the quadrupole is mainly distributed at the separation points of incoming flow and its drag zone. The dipole sound source is mainly caused by the two-step gradient of dynamic pressure in the transverse direction (y-direction) at both sides of the cylinder. The above conclusions can provide a theoretical basis for the aerodynamic noise control.

aeroacoustic noise; cylinder with limited length; sound source equation; dipole sound source

O422.8

A

1000-3630(2019)-01-0005-10

10.16300/j.cnki.1000-3630.2019.01.002

2018-07-12;

2018-08-28

上海市地面交通工具空气动力与热环境模拟重点实验室资助项目、国家自然科学基金资助项目(51375342)。

杨志刚(1961－), 男, 上海人, 博士, 研究方向为汽车空气动力学。

王毅刚,E-mail: yigang.wang@sawtc.com