适于泥石流除噪的EMD联合小波阈值除噪方法

朱凤杰，焦瑞莉，滕鹏晓



适于泥石流除噪的EMD联合小波阈值除噪方法

朱凤杰1，焦瑞莉1，滕鹏晓2

(1. 北京信息科技大学信息与通信工程学院，北京 100085；2. 中国科学院声学研究所，北京 100190)

次声传感器采集到的泥石流次声信号中包含有大量的无关干扰信号，严重影响信号的分析与评估。针对含噪泥石流信号中无法准确确定噪声频段的特点，以及传统经验模态分解(Empirical Mode Decomposition, EMD)联合小波阈值去噪方法无法智能分辨噪声所在频段的缺点，提出了信号经EMD分解后，基于相关性选择噪声频段的方法。首先利用EMD分解获取信号的固有模态函数(Intrinsic Mode Function, IMF)分量，然后计算各个IMF分量与原始信号的相关性，根据相关性大小确定IMF噪声频段，然后采用小波阈值去噪方法对噪声频段进行处理，最后对处理后的信号进行重构得到去噪泥石流信号。通过模拟实验分析，证明该方法具有智能选择噪声频段的能力，是一种更适于泥石流信号的去噪方法。

泥石流次声信号；经验模态分解；小波阈值去噪；相关性

0 引言

在泥石流发生过程中，泥土土质的破坏以及岩石的破碎会产生次声波信号。次声波拥有衰减慢，穿透力强的声学信号特点，可以利用该特点实现次声发生源的准确定位[1]。近几年来，基于次声波的泥石流检测技术已经逐渐成为了泥石流检测研究方向的一大热点，随着次声探测传感器性能的提高以及信号处理技术的提升，国内外也开始不断给出了泥石流次声研究的新成果，已经可以更加准确的定位泥石流次声信号的能量分布范围以及主频频段等信号特征[2]。

在泥石流次声传感器采集到的信号中，噪声可能存在于任何一个频段中[3]。传统的经验模态分解(Empirical Mode Decomposition, EMD)联合小波阈值去噪方法中只能对某一个频段的噪声进行硬性去噪[4]，缺乏灵活性并且容易对真实信号造成损伤，由此提出了适合于泥石流信号处理的EMD分解联合小波阈值去噪方法。

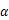
1 方法及步骤

1.1 EMD分解

EMD分解是一种不需要先验基底的自适应分解方法，信号可以分解为从高频到低频排列的若干个固有模态函数(IMF)。

EMD分解算法步骤[5]如下：

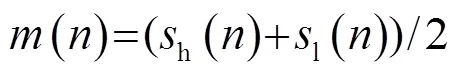
1.2 小波阈值去噪

传统的滤波去噪方法在信号处理过程中都存在着比较严重的缺陷，比如，理想低通滤波器会出现严重的抖动现象；切比雪夫滤波器在通带和阻带范围内的幅频特性有波动；巴特沃斯滤波器的幅频特性是单调下降的[6]。这些经典的信号去噪方法在实现噪声平滑的过程中必然会引起信号的模糊而降低其清晰度，使其滤波后的熵值增高，从而无法很好地刻画信号的非平稳性。而小波变换可以对信号进行多尺度细化，适合时变和非平稳信号的时频分析需求[5]，已成为信号去噪的主要方法之一。

小波阈值去噪的主要步骤如下[7]：

(1) 选取合适的小波以及确定合适的小波分解层数，得到相应的小波分解系数。

(2) 选取合适的阈值，并对上一步得到的小波系数进行阈值处理。

(3) 小波重构，通过得到的新的阈值，对信号进行重构得到去噪后的信号。

2 改进的EMD联合小波阈值去噪

2.1 方法介绍

传统的EMD联合小波阈值去噪方法，只能凭借经验对一些固定的含噪IMF频段进行除噪处理，而在泥石流次声信号中，无法准确确定某一个频段为噪声频段。因此需要通过一种更加灵活的方式去确定含噪IMF频段，然后再对其进行除噪处理。

针对传统的EMD联合小波阈值去噪方法在泥石流信号应用上的不足，对其进行了改进。首先对次声传感器测得的含噪泥石流信号进行EMD分解，由于泥石流信号会在含噪泥石流信号中占据较大的比重，因此可以通过计算每一个IMF分量与含噪信号的相关性来确定每一个IMF分量是否包含重要的泥石流信息。每一个IMF分量与原始信号的相关系数可以表示为

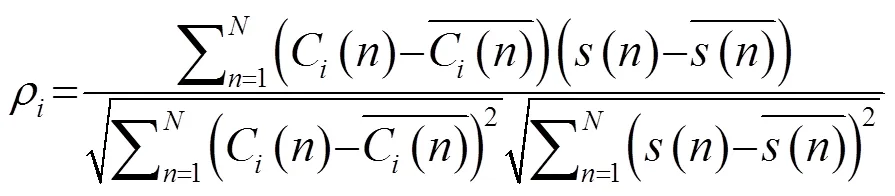
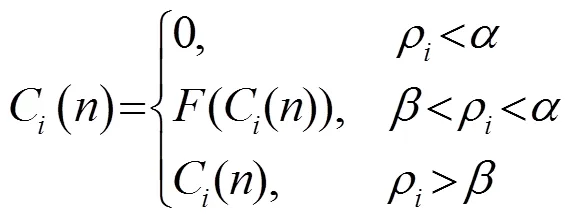
最后将去噪后的IMF分量与直接保留的相关性较高的IMF分量进行重构得到去噪后的信号：

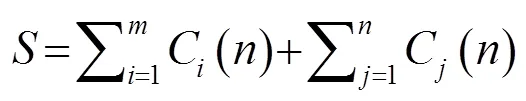
2.2 小波基的选择与阈值的选取

小波阈值去噪过程中最重要的就是小波基的选择，常用的小波基函数的特征如表1所示。表中CWT为连续傅里叶变换(Continuous Wavelet Transform)，DWT为离散傅里叶变换(Discrete Wavelet Transform)，为消失矩阶数。由于泥石流信号是一种存在大量突变的非线性、非平稳信号，因此一般选择具有正则性、紧支性和消失矩的小波作为小波基。由于Symlet小波函数在正则性、紧支性等方面都要优于其它小波，并且Symlet小波是对Daubechies (dbN)小波的一种改进，不仅具备小波光滑、误差不容易被察觉、信号重构过程比较光滑的特点，同时具备了较好的正则性。Symlet小波在连续性、支集长度、滤波器长度等方面与Daubechies小波一致[8]，并且Symlet小波具有更好的对称性，即一定程度上能够减少对信号进行分析和重构时的相位失真[9]。因此选用Symlet小波作为小波阈值去噪的小波基。

表1 常用小波函数的主要特征

小波阈值去噪过程中阈值的选取分为硬阈值和软阈值两种方式[10]，硬阈值的表达式为

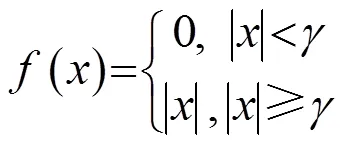
软阈值的表达式为

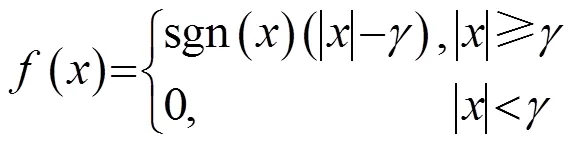
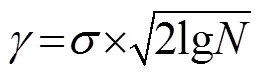
由于硬阈值的去噪方法在连续性和去噪效果上都没有软阈值去噪方法好[11]，因此选择软阈值的处理方式。

3 模拟泥石流信号仿真分析

为了验证EMD分解与小波阈值联合去噪在泥石流次声信号去噪中的性能，根据泥石流次声信号的非线性、非平稳特性，通过仿真实验获得的模拟泥石流信号如图1(a)所示，为该信号添加的真实采集的泥石流原始背景噪声如图1(b)所示，加噪后的信号如图1(c)所示。

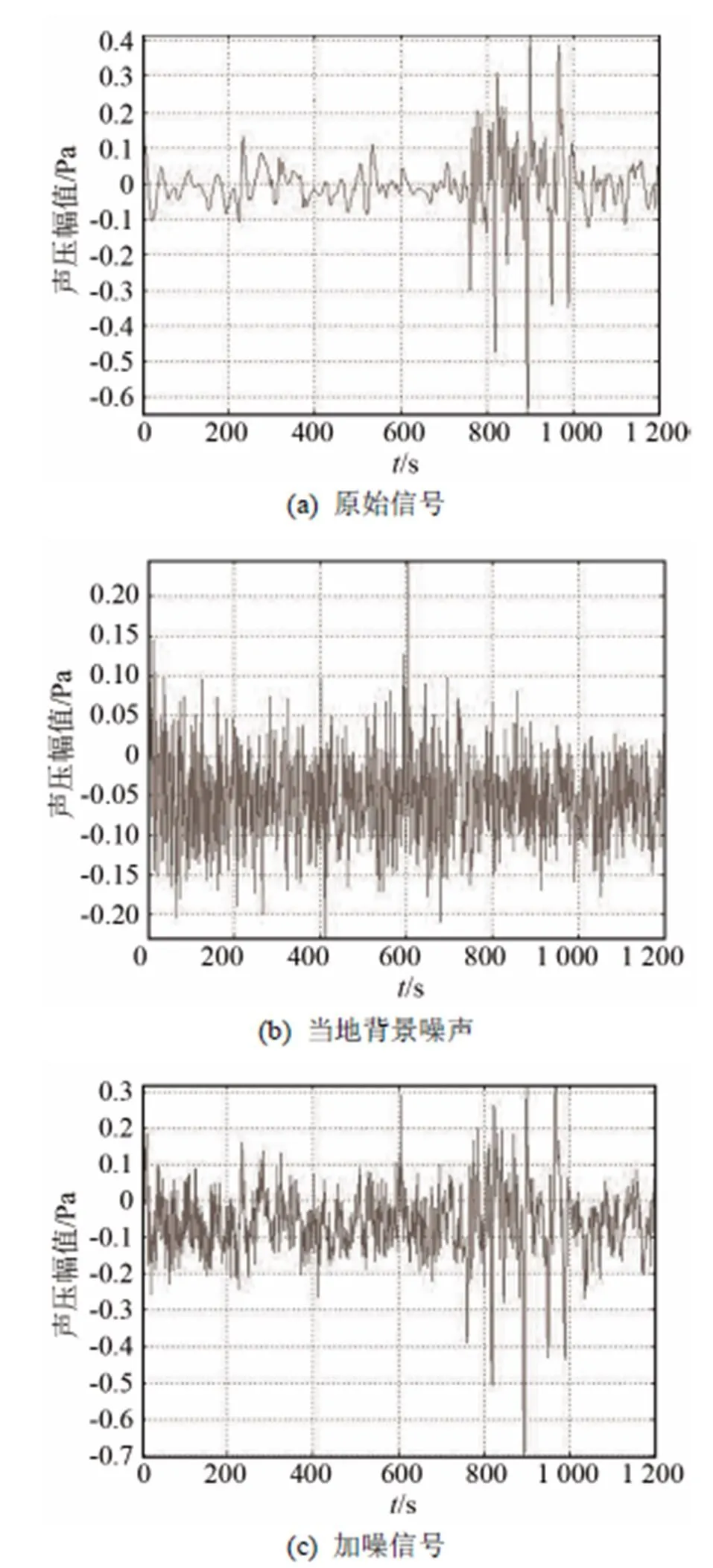
图1 原始信号与加噪信号对比图

采用小波阈值去噪、传统EMD分解加小波阈值去噪与本文方法去噪三种方式，分别对加噪后的信号进行去噪处理，得到去噪信号的时域对比图见图2，信号的信噪比及与原始信号的相关性见表2。

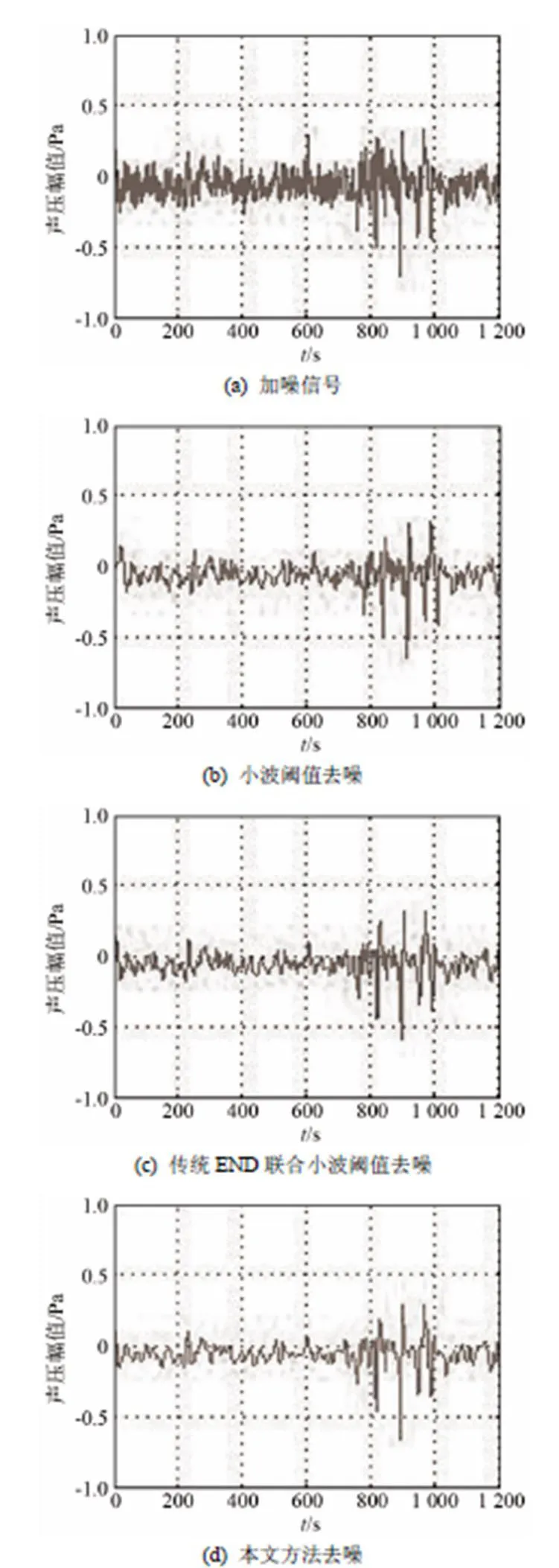
图2 不同方法去噪后的时域信号对比图

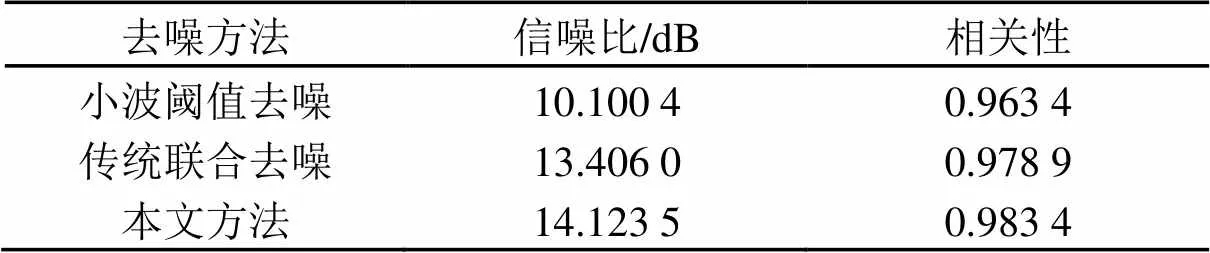
表2 三种去噪算法信噪比与相关性表

从表2中数据分析可知，小波阈值去噪和传统EMD联合小波阈值去噪得到的去噪信号，在信噪比上要略低于本文方法去噪后得到的去噪信号的信噪比。去噪后的信号与原始信号的相关性也略低于本文方法的结果，即用改进的EMD分解与小波阈值联合去噪方法得到的信号，在信噪比和原始信号的相似程度上都要好于前两种去噪方法。

对去噪后的信号进行进一步的频谱分析，并求得每一种去噪方法去噪后的信号与原始信号的频谱差，如图3所示。

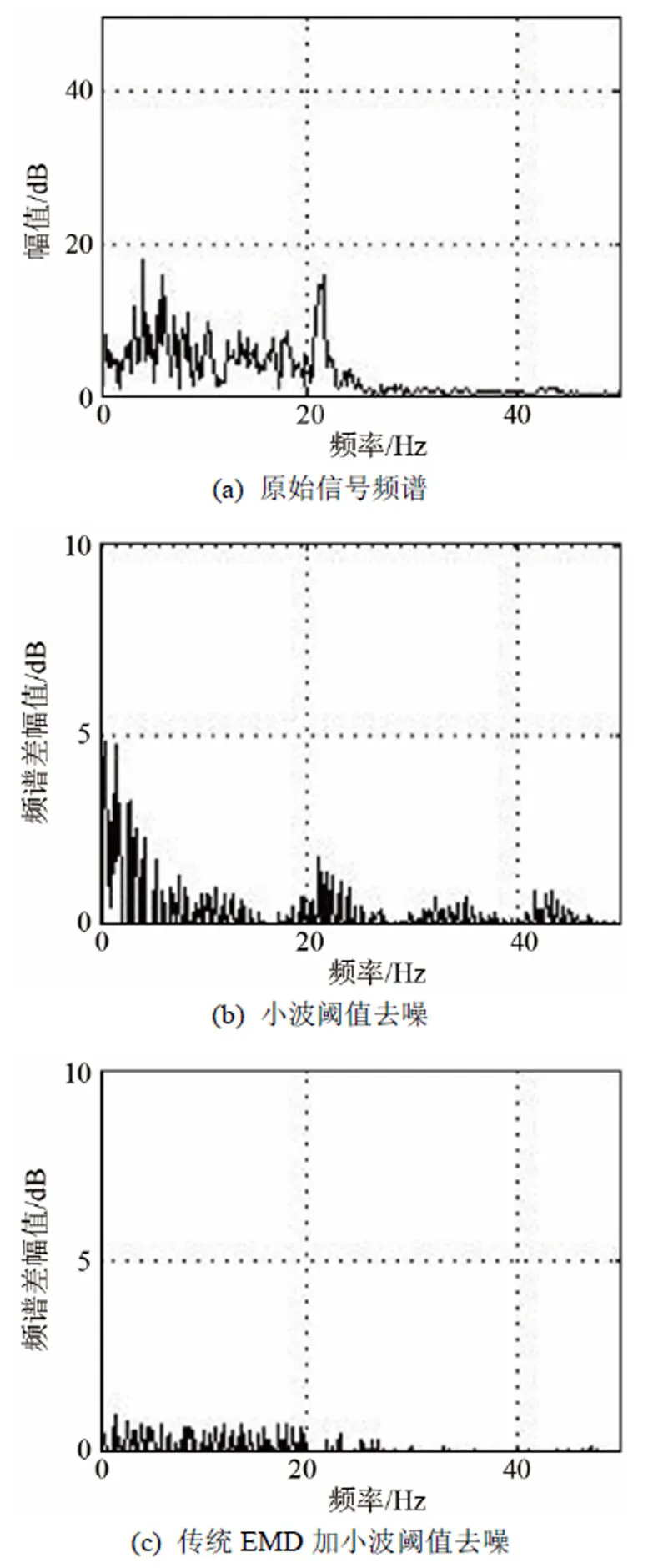
从图3可以明显看出，传统的EMD联合小波阈值去噪的方式得到的频谱差，虽然在高频部分拥有很好的去噪效果，但是在低频部分却失去了更好的去噪性能，相对而言，改进的方法能智能选择噪声频段，在高频和低频段均拥有很好的去噪性能，从而更适于泥石流次声信号的处理。

4 真实泥石流信号分析处理

4.1 信号数据来源

实验中用到的数据来源于2014年8月4日云南东川蒋家沟地区的泥石流事件。图4为原始信号的时域分布图。

4.2 信号的EMD分解与分量选择

通过对原始信号进行EMD自适应分解可以得到如图5所示的20个IMF分量，频率由IMF1到IMF20依次递减。

图4 原始信号时域分布

计算每一个IMF分量与原始信号的相关性，得到相关性分布折线图如图6所示。

以模拟泥石流信号作为分析依据，以不同的、值计算去噪重构信号与原始信号的相关性，通过定量分析，发现当、值将数据频段切割成20%左右的噪声频段和10%左右的保留信号频段时，去噪重构信号与原始信号的相关性最高。

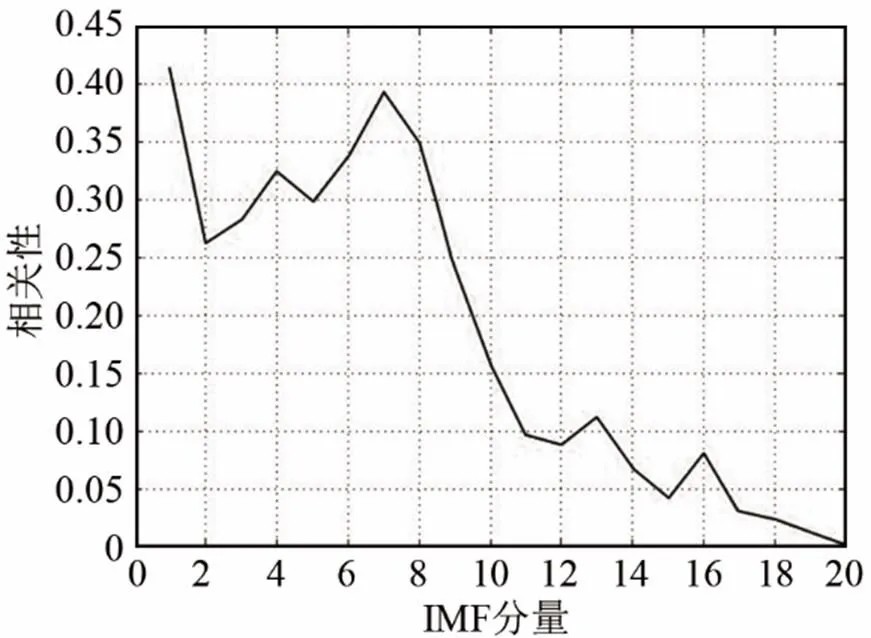
图6 IMF分量的相关性分布图

因此，根据当地环境的噪声特点，将噪声频段设置为原始数据的20%，即将舍去IMF分量的阈值下限设置为0.05；将真实泥石流信号频段设置为原始信号的10%，即将保留IMF分量的阈值上限设置为0.37。

从图6可以看出，固有模态函数IMF15、IMF17～IMF20与原始信号的相关性低于0.05，完全可以作为无关干扰信号进行舍弃。IMF1和IMF7分量与原始信号的相关性较高，均达到0.37以上，故包含有重要的泥石流信号信息，为防止重要信息丢失，对其进行完全保留，不再进行小波阈值去噪处理。

4.3 小波阈值除噪与信号重构

通过对EMD分解得到的IMF分量进行选择，舍弃了低于阈值下限的4个IMF分量，完全保留了高于阈值上限的2个IMF分量，对于剩余的13个IMF分量，由于其既包含有相当量的泥石流信号信息，又包含有大量的干扰噪声，因此需要对其进行去噪处理。

对每一个IMF分量利用Symlet5小波作为小波基进行去噪后得到的信号如图7所示。

与图5的各含噪IMF分量相比，经小波阈值去噪后，信号在不同频段的噪声含量均有所降低，在保留泥石流重要信息的同时，可以智能地分辨噪声所在频段，不再拘泥于消除某一固定频段的噪声，因此是针对泥石流次声信号处理的一种更灵活、可靠的去噪方式。

将小波阈值去噪后的IMF分量与相关性最高的两个IMF分量进行重构，可以得到如图8所示的重构信号。

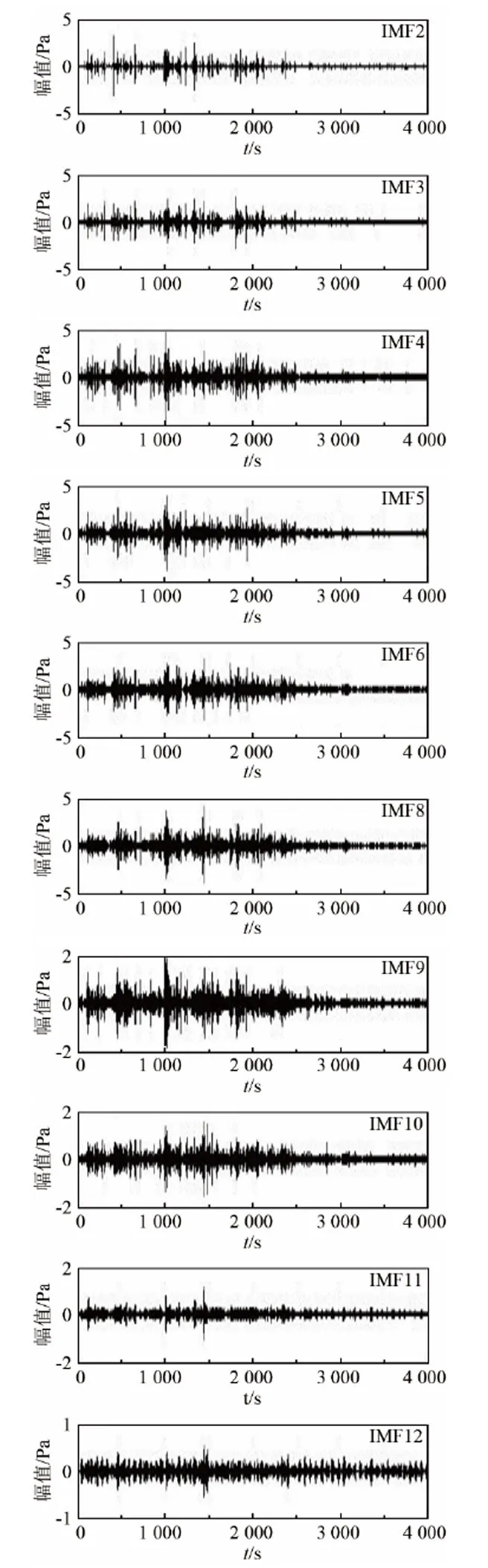
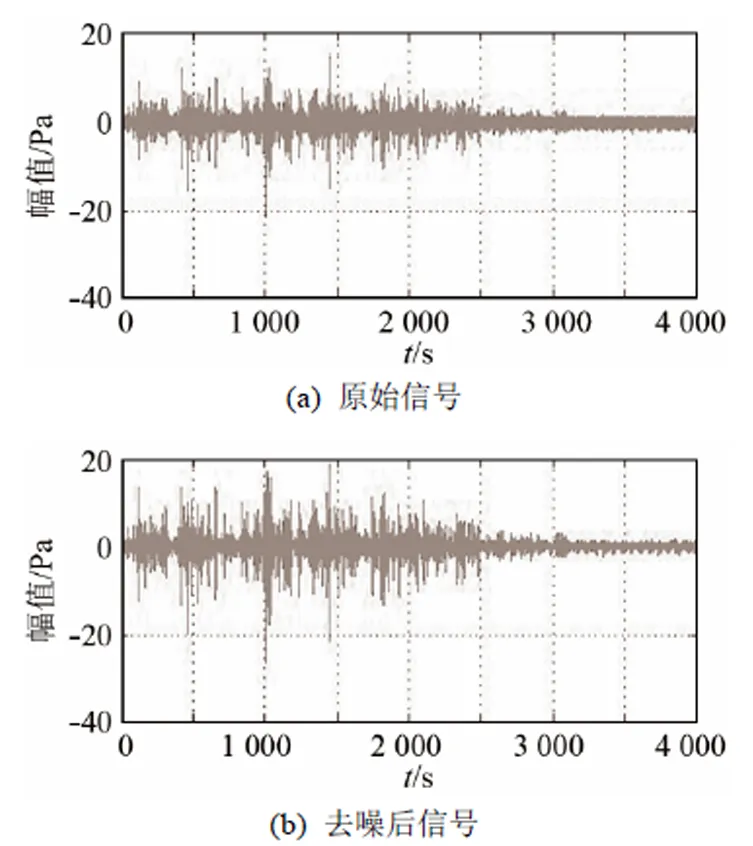
图8 原始信号和除噪后重构信号对比图

4.4 重构信号时频分析

经过EMD分解和小波阈值联合去噪之后，得到了去除噪声之后的泥石流信号。为进一步对泥石流信号的频段信息进行研究，在此对重构信号进行小波时频分析。

这里选择cmor小波作为小波时频分析的小波基，小波带宽参数为3，中心频率为3 Hz，得到原始信号的小波时频图与重构信号的小波时频图如图9所示。

通过图9中的时频分析对比可以发现，经EMD分解与小波阈值联合去噪后的信号滤除了大量的高频噪声，同时去除了一些无关的低频细节分量，从而可以获得更加可靠的泥石流信号。对图9进一步分析可以看出，在泥石流发生时(1 000～1 500 s)，次声信号能量开始出现明显的聚集，且能量主要集中在2～6 Hz频段，在整个泥石流事件中，信号在10 Hz频段以下都有明显的能量变化。

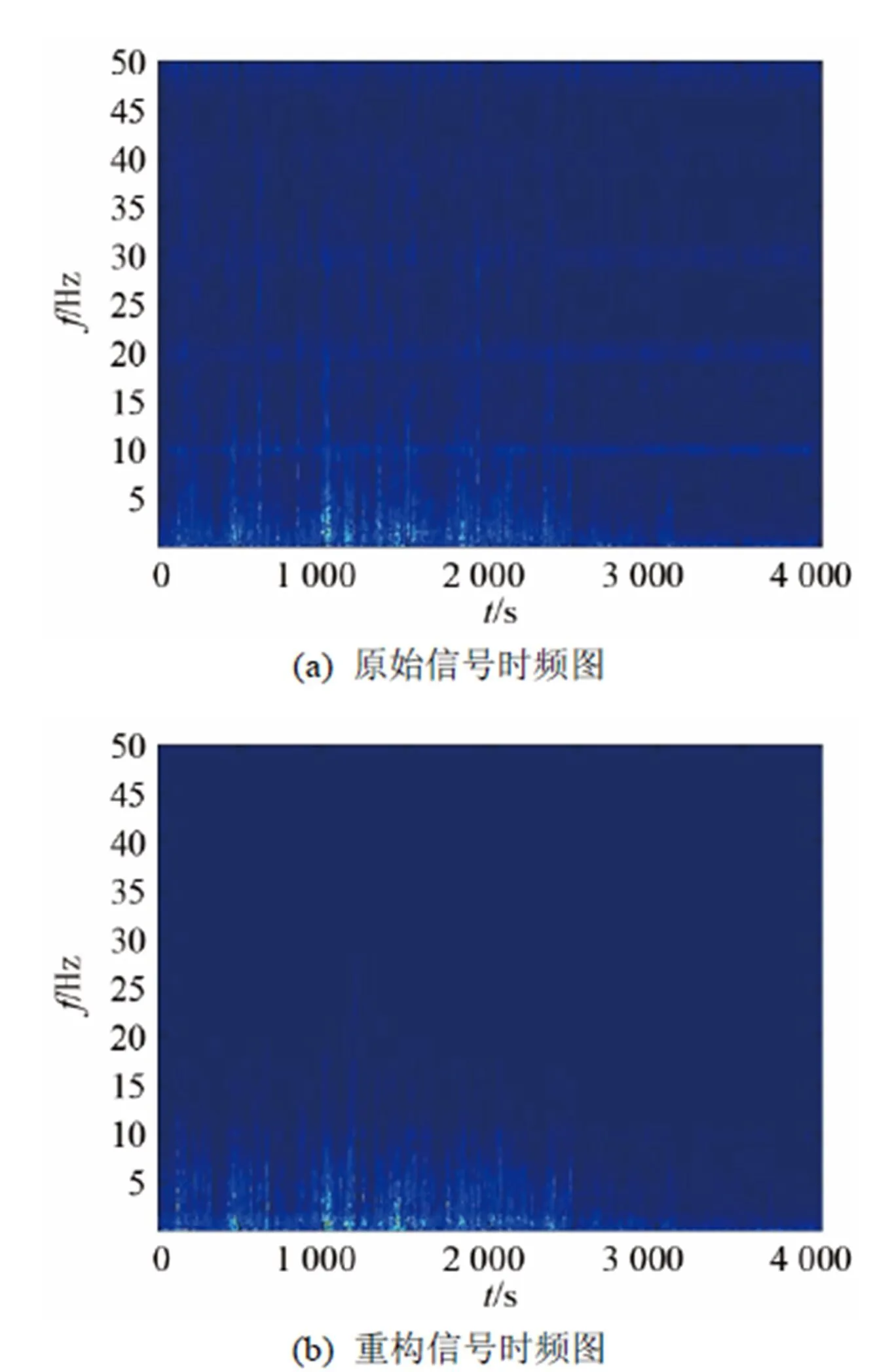
图9 原始信号和重构信号的小波时频分析图

5 结论

实验证明本文提出的方法更适合于泥石流信号的去噪处理，其在滤除了高频段信号噪声的同时还能对低频段的信号进行相应的选择处理，由于对与原始信号具有高相关性的IMF分量不进行去噪处理，因此又能更好地保护信号细节信息。通过对去噪后的泥石流信号的进一步时频分析，得到泥石流信号主要频率范围为2～6 Hz，且在泥石流发生过程中，整个10 Hz以下频段都有明显的能量变化。

[1] 谢涛, 徐小林, 陈洪凯. 泥石流拦挡坝研究现状及发展趋势[J]. 中国地质灾害与防治学报, 2017, 28(2): 137-145.

XIE Tao, XU Xiaolin, CHEN Hongkai. Research status and development trend of debris flow dam[J]. The Chinese Journal of Geological Hazard and Control, 2017, 28(2): 137-145.

[2] 李朝安, 胡卸文, 王良玮. 山区铁路沿线泥石流次声监测预警方法[J]. 声学技术, 2012, 31(4): 351-356.

LI Chao’an , HU Xiewen, WANG Liangwei. Infrasound monitoring and early warning of debris flow along montanic railway line[J]. Acoustic Technique, 2012, 31(4): 351-356.

[3] 郑菲. 次声波源产生的机理及有限元模拟[D]. 成都: 成都理工大学, 2015.

ZHENG Fei. Infrasound source generation mechanism and finite element simulation[D]. Chengdu: Chengdu University of Technology, 2015.

[4] 赵宇翔, 刘文会, 苏亮亮, 等. 小波分析在振动信号去噪中的应用研究[J]. 吉林建筑大学学报, 2016, 33(5): 27-30.

ZHAO Yuxiang, LIU Wenhui, SU Liangliang, et al. Application of wavelet analysis in vibration signal denoising[J]. Journal of Jilin Jianzhu University, 2016, 33(5): 27-30.

[5] 徐洁, 王阿明, 郑小锋. 基于小波阈值去噪的心电信号分析[J]. 计算机仿真, 2011, 28(12): 260-263.

XU Jie, WANG Aming, ZHENG Xiaofeng. ECG signal analysis based on wavelet threshold denoising, 2011, 28(12): 260-263.

[6] 曾敬枫. 基于MATLAB不同小波基的小波阈值图像去噪算法[J]. 智能计算机与应用, 2016, 6(4): 75-77.

ZENG Jingfan. Wavelet threshold image denoising algorithm based on different wavelet bases of MATLAB[J]. Intelligent Computer and Applications, 2016, 6(4): 75-77.

[7] 陶伟, 李文尧, 张登, 等. 基于小波变换的TEM信号处理中小波基函数的选择[J]. 中国锰业, 2016, 34(6): 175-176.

TAO Wei, LI Wenyao, ZHANG Deng, et al. Selection of wavelet basis functions in TEM signal processing based on wavelet transform[J]. China’s Manganese Industry, 2016, 34(6): 175-176.

[8] 王剑平, 张捷. 小波变换在数字图像处理中的应用[J]. 现代电子技术, 2011, 34(1): 91-94.

WANG Jianping, ZHANG Jie. Application of wavelet transform in digital image processing[J]. Modern Electronics Technique, 2011, 34(1): 91-94.

[9] 刘雪勇. 次声信号特征提取与分类识别研究[D]. 北京: 中国地质大学(北京), 2015.

LIU Xueyong. Research on infrasound signal feature extraction and classification recognition[D]. Beijing: China University of Geosciences (Beijing), 2015.

[10] LIU D L. Monitoring and recognition of debris flow infrasonic signals[J]. Journal of Mountain Science, 2015, 12(4): 797-815.

[11] 曾宪伟, 赵卫明, 师海阔, 等. 利用小波包变换对地震信号进行时频分析时小波基函数的选取木[J]. 地震研究, 2010, 33(4): 323-328.

ZENG Xianwei, ZHAO Weiming, SHI Haikuo, et al. Selection of wavelet basis function in time-frequency analysis of seismic signals by wavelet packet transform[J]. Journal of Seismological Research, 2010, 33(4): 323-328.

EMD decomposition and wavelet threshold denoising method for removing noise from debris flow signals

ZHU Feng-jie1, JIAO Rui-li1, TENG Peng-xiao2

(1. School of information and Communication Engineering, Beijing Information Science and Technology University, Beijing 100085, China; 2.The Institute of Acoustics of the Chinese Academy of Sciences,Beijing 100190, China)

Infrasound signals collected by infrasound sensor contain a large number of irrelevant interference signals, which seriously affect the analysis and evaluation of the signals. In view of the characteristics that the noise frequency band can not be accurately identified in the noisy debris flow signal and the shortcoming that the traditional method of empirical mode decomposition (EMD) combined with wavelet threshold denoising can not intelligently distinguish the frequency band where the noise is located, a correlation based method of selecting the noise frequency band is proposed after decomposing the EMD signal. Firstly, the EMD decomposition is used to obtain the intrinsic mode function (IMF) components of the signal, and then the correlation between each IMF component and the original signal is calculated. The frequency band of IMF noise components is selected according to the level of correlation, and then processed by the wavelet threshold de-noising method. Finally, the processed IMF components are reconstructed to get the denoised infrasound signal of debris flow. The simulation results show that this method has the ability to select the noise frequency band intelligently, and is a more suitable denoising method for debris flow signals.

debris flow infrasound signal; empirical mode decomposition (EMD); wavelet threshold denoising; correlation

O425+.3

A

1000-3630(2019)-01-0083-08

10.16300/j.cnki.1000-3630.2019.01.014

2018-01-14;

2018-02-17

北京信息科技大学横向课题(9161624104)。

朱凤杰(1991－), 男, 山东日照人, 硕士研究生, 研究方向为次声信号处理。

朱凤杰, E-mail: fengjie_zhu @qq.com