高斯色噪声下的子阵平滑主模式抑制波束形成

邵鹏飞，邹丽娜



高斯色噪声下的子阵平滑主模式抑制波束形成

邵鹏飞，邹丽娜

(声呐技术重点实验室杭州应用声学研究所，浙江杭州 310012)

实际海洋波导是一种具有空-时相关性的衰落信道，且其驻留的海洋环境背景噪声场呈现非均匀各向异性的特性，噪声场时空相关性并非函数，大孔径声呐的探测性能会受到很大影响。将背景噪声建模为有色高斯随机过程，设计基于子阵平滑的主模式抑制(Dominant Mode Rejection, DMR)波束形成算法，以实现小快拍数条件下具有去相关作用的自适应处理，较好地提高了大孔径阵声呐在高斯色噪声环境下的探测能力。模拟仿真结果表明，该方法具有良好的抑制高斯色噪声的能力。

高斯色噪声；子阵平滑；主模式抑制；波束形成

0 引言

海洋背景噪声场并不能等同建模为均匀各向同性的白高斯噪声随机过程，而是被表征为受边界和动力学等因素影响，具有一定空-时相关性的随机场。为了解决环境噪声的动力学特性影响，Messerschamit等提出了一种基于降秩处理的主模式抑制(Dominant Mode Rejection, DMR)波束形成方法[1]。在小快拍数条件下，作者根据文献[2]中的N/E-阿凯克信息准则(N/E-Akaike Infromation Criterion,N/E-AIC)方法对子空间维度进行估计[3]，优化了DMR算法性能(DMR方法的设计前提是噪声背景为白高斯特性[4-6])。对于有色高斯噪声背景，采用该方法重构得到的采样协方差矩阵(Sampling Covariance Matrix, SCM)，在结构上与实际数据下的系综协方差矩阵(Ensemble Covariance Matrix, ECM)之间会产生比较严重的失配，因而会导致其性能大大下降。

目前，噪声及干扰的相关性对阵处理影响的研究，已发表的文章较多[7-10]。大多数解决方法都是建立在解相关技术的基础上，一种比较简单有效的去相关方法就是引入子阵平滑处理，利用空间平滑提高小快拍数时的自适应波束形成性能[11-14]。在此基础上，通过基于子空间维度估计的DMR方法(N/E-AIC准则下子空间维数估计的新DMR方法(New Dominant Mode Rejection, NDMR)，并引入子阵平滑(Subarray Smoothing, SS)技术来实现有色高斯噪声背景下的自适应目标检测和方位估计。

本文将构建设计小快拍数样本下子阵平滑主模式抑制算法(Subarray Smoothing-New Dominant Mode Rejection, SS-NDMR)。同时，研究在高斯色噪声背景下SS-NDMR算法的性能，并通过模拟数据仿真，以验证本方法的有效性。

1 阵列信号模型

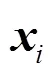
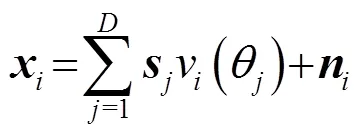
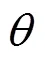
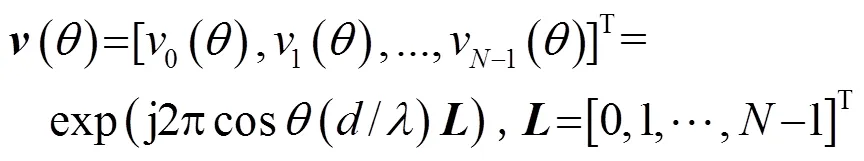
当背景噪声为各项均匀同性的白高斯噪声时，由观察模型可以得到接收信号的系综协方差矩阵(Ensemble Covariance Matrix, ECM)，理论上可以将其表示为如下形式：

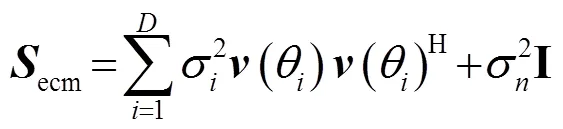
当背景噪声为有色高斯噪声时，其形式表示为

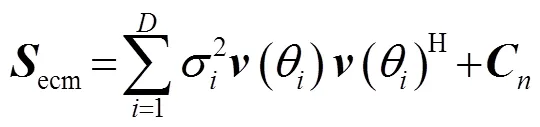
若将噪声建模为随机过程，常见的有色高斯噪声可以看作为以白高斯随机信号激励的自回归(Autoregression, AR)随机过程。色高斯噪声在过程上具有一定的相关性，因而相对于白噪声，色噪声的随机样本的自相关图会产生较高的旁瓣，如图1所示。

色噪声的相关特性对常见的相干处理以及白噪声模型自适应处理均会带来不利的影响。

2 SS-NDMR算法

本文研究的重点是解决色高斯背景下的自适应波束形成算法，采用的两项关键技术核心是子阵平滑(SS)及主模式抑制(DMR)，在具体的算法实现中采用了DMR的一个算法特例NDMR，其仍为DMR方法的延伸，因此，本节标题算法简写中将其表述为SS-NDMR。

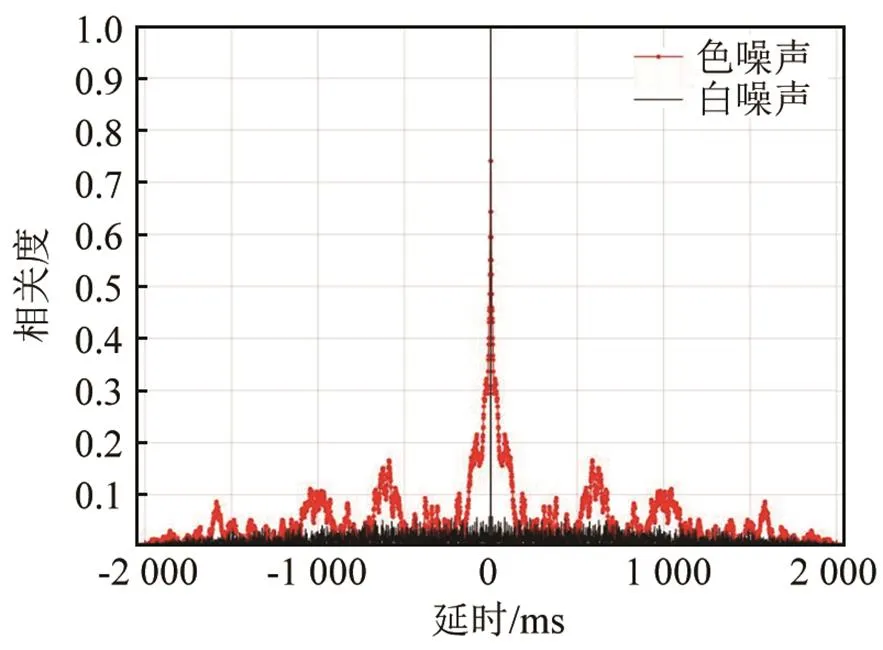
图1 白高斯噪声序列和色高斯噪声序列的自相关图

2.1 NDMR波束形成

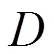
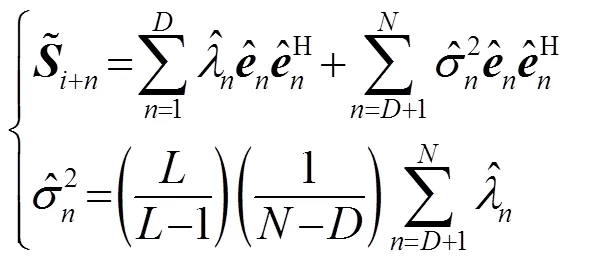
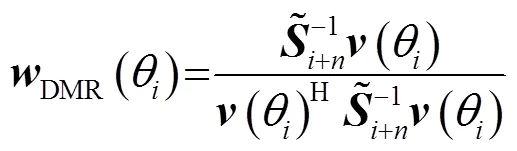
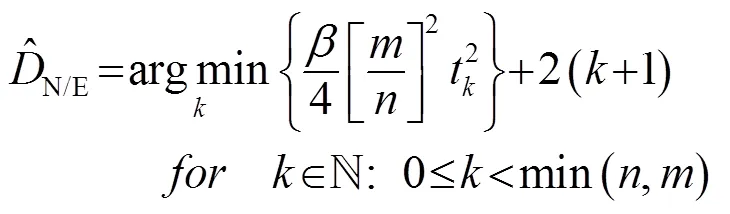
其中，

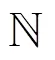
而且通过性能分析证明了维数的估计准确性对输出信干噪比((Signal to interference plus noise power ratio, SINR)有一定的影响，在白高斯背景下，NDMR的性能相对于一般DMR处理更具有最佳性和稳健性。

2.2 SS-NDMR波束形成

通常的阵列信号处理算法建立在信号子空间与噪声子空间正交，且各通道噪声互不相关的条件下，因而通过相干处理来获取对应的信号增益。当面临实际背景为色高斯噪声时，为了达到与理论接近的增益，需要引入去相关处理技术。由于子阵平滑处理具有明显的去相关作用，本文将其引入NDMR算法中。

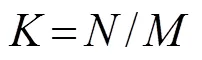
定义第个前向滑动的子阵输出为

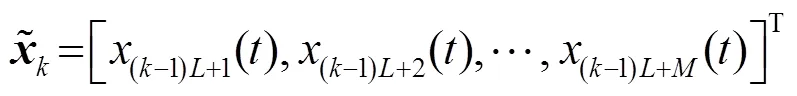
则对第K个子阵输出，引入NDMR算法运算得到相应的子阵权重向量，其中。然后利用所求得的各子阵权重向量，通过相位补偿、加权求和，重构为最终的SS-DMR算法权重向量。该算法结构如图2所示。

当接收阵为128元均匀线阵，且背景噪声服从色高斯分布时，设定环境中存在一个方位角为68°的静止目标。在不同信噪比下，通过1 000次蒙特卡洛仿真，给出样本快拍数均为32，利用CBF、NDMR、MVDR以及SS-NDMR处理得到的对应的检测能力，其对应的色高斯背景下的检测概率曲线如图3所示。

从图3可以看出，在有色高斯噪声背景下，具有去相关处理的SS-NDMR方法对目标的检测，相比于NDMR、MVDR和CBF方法有更高的检测概率。其中CBF方法的检测性能最差。同时，由于受噪声相关性的影响，使基于白噪声建模优化的NDMR方法对主模式维度的估计失配，因而性能下降也比MVDR方法明显。

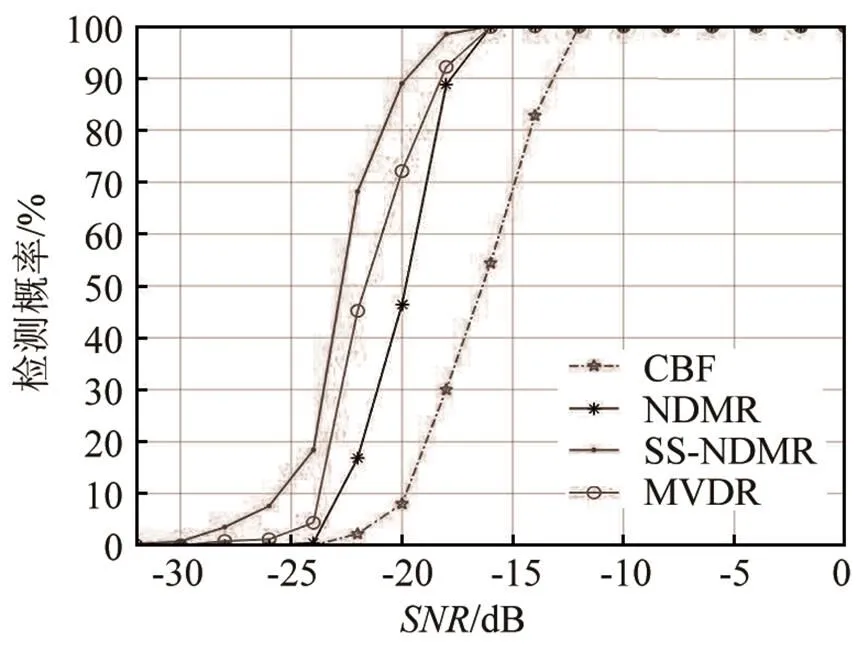
图3 色高斯背景下不同波束形成算法的的检测性能曲线

3 仿真数据处理

本文针对SS-NDMR方法在色高斯噪声背景下的检测性能进行仿真验证。仿真设定为，环境中存在8个目标，且目标源信号相互独立。接收阵是阵元数为128元、阵元间距为4.8 m的均匀直线阵，处理频带为140～170 Hz，采样率为5 kHz。

目标参数设置分别为：1#(相对正北坐标初始方位140o，距离12 km，航向110o，航速2 kn，信噪比-13 dB)；2#(初始方位105o，距离24 km，航向285o，航速4 kn，信噪比-12 dB)；3#(初始方位90o，距离32 km，航向20o，航速10 kn，信噪比-12.5 dB)；4#(初始方位65o，距离20 km，航向135o，航速18 kn，信噪比-13 dB)；5#(初始方位50o，距离16 km，航向115o，航速12 kn，信噪比-13dB)；6#(初始方位25o，距离6 km，航向155o，航速10 kn，信噪比-13.5 dB)；7#(初始方位11o，距离2 km，航向0o，航速0 kn，信噪比-7 dB)；8#(初始方位60o，距离10 km，航向215o，航速9 kn，信噪比-22 dB)。

基阵姿态航向为相对于正北0o方向，目标的运动轨迹极坐标图如图4所示。

在快拍数均为32的条件下，分别比较了CBF、NDMR、MVDR、SS-NDMR的处理性能，其中SS-NDMR的子阵维度为64，子阵平滑数目为48。比较结果如图5所示。

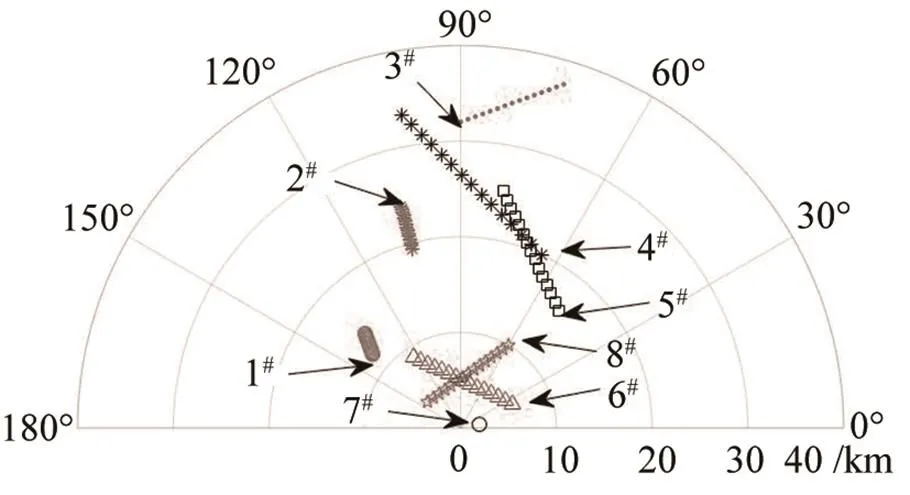
图4 目标运动轨迹极坐标图

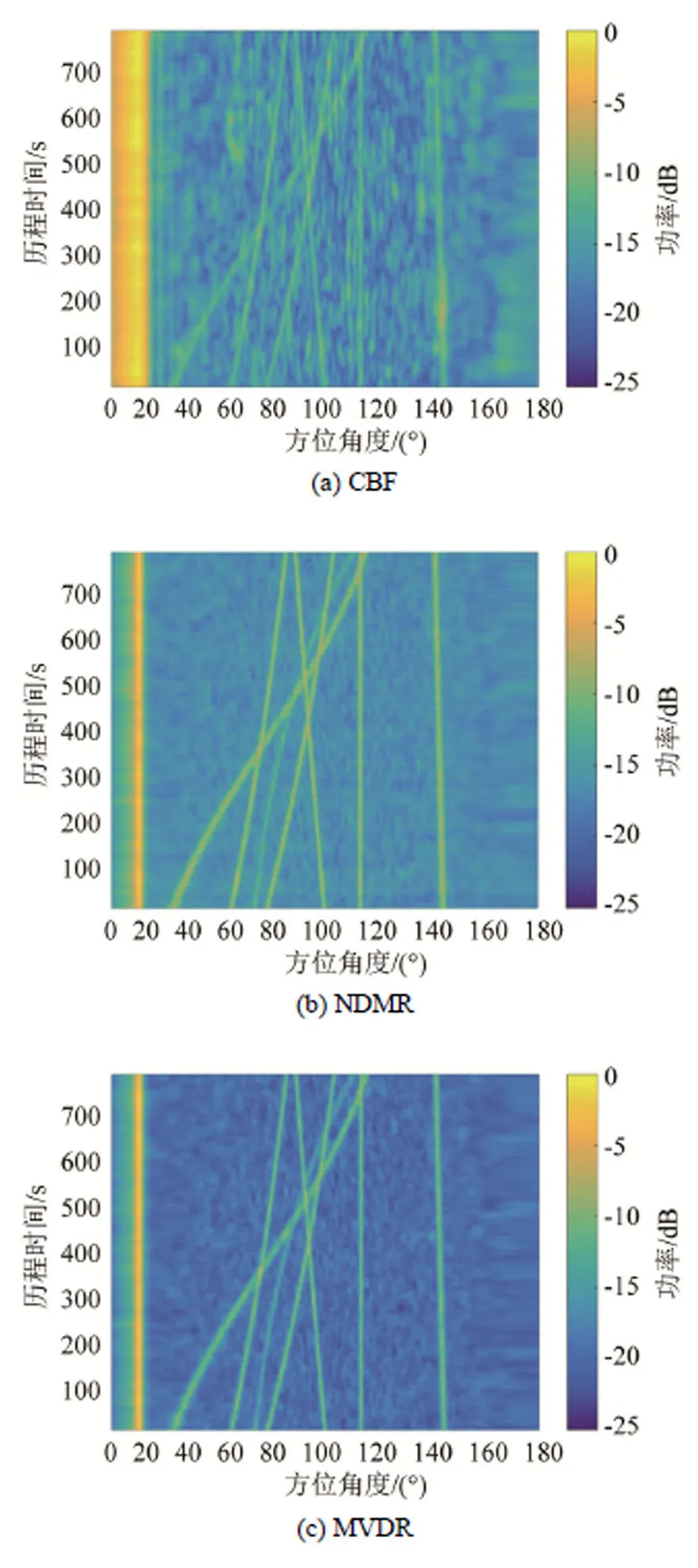
从以上仿真结果可以看出，比较CBF、NDMR、MVDR、SS-NDMR四种不同处理方式下的结果，在有色高斯噪声背景下，SS-NDMR方法对目标的检测性能最佳，除此之外，图5(b)中NDMR方法和图5(d)中SS-NDMR方法所估计的目标空间波数谱均较宽，原因是两种方法降维抑制噪声所致，而SS-NDMR方法因为空间平滑最终将以损失阵孔径为代价，而图5(c)中MVDR方法则不存在此问题。由图5(a)和图6可以看出，基于相干性处理的CBF受背景相关性影响，只能对相对较强的目标进行有效检测，弱信号基本被背景湮没而没有一定的输出增益；比较图5(b)、5(c)和5(d)，NDMR、MVDR和SS-NDMR 3种自适应处理方法均可以对设定的8个目标进行有效检测，其中SS-NDMR对噪声背景抑制效果最佳，相比于另外两种方法检测性能更具优势，这一分析结果通过图6的片段显示及表1的四种算法输出信噪比统计可以更明显地体现，该结论与图3的性能分析结果一致。

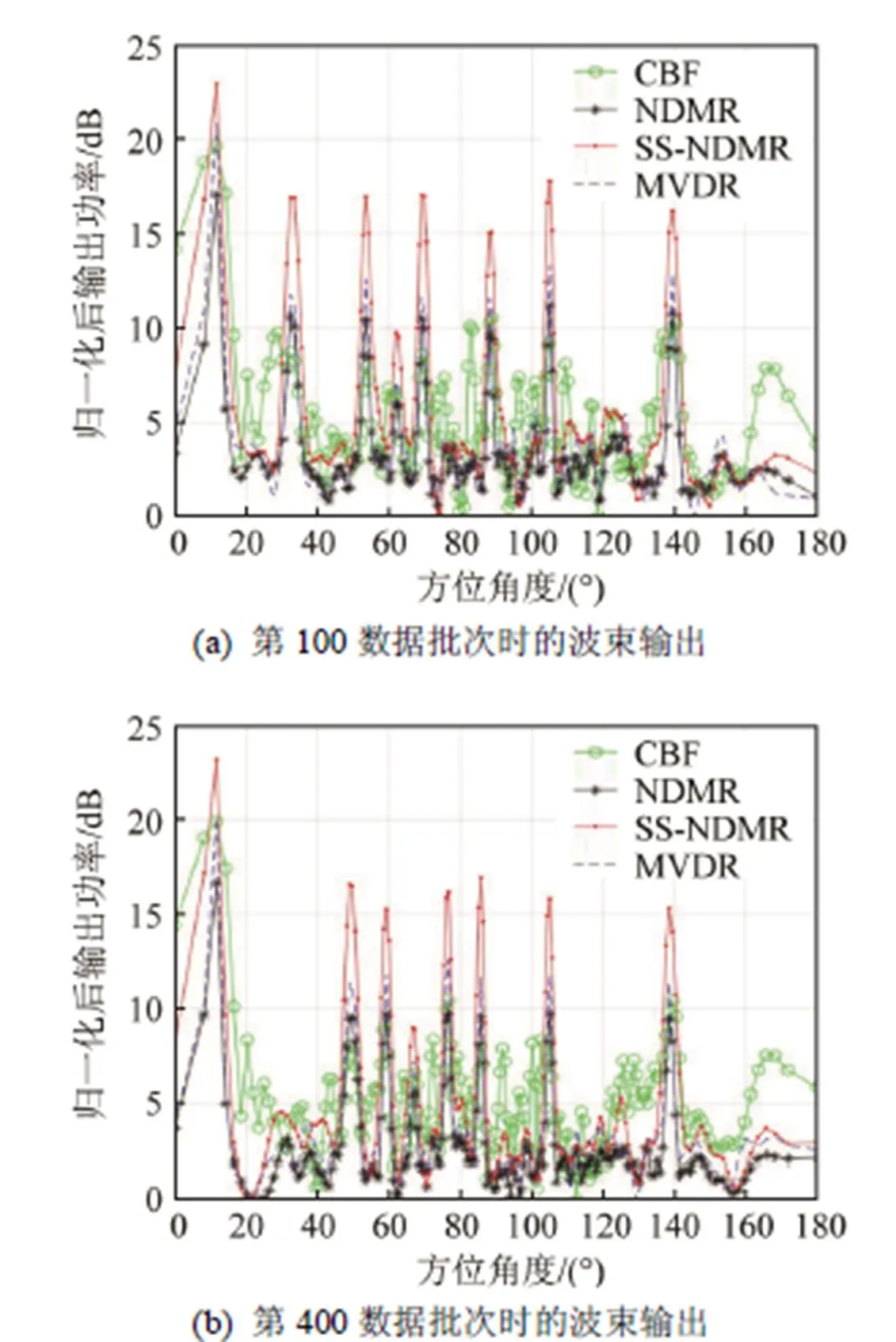
图6 不同波束形成算法对第100和第400数据批次的波束输出

表1 不同波束形成算法得到的第100和第400数据批次中第8号弱目标的输出信噪比(dB)

Table 1 The output SNRs of the 8th weak target in the 100th and the 400th batches of data by different beamforming algorithms

注：初始方位60°，距离10 km，航向215°，航速9 kn，信噪比-22 dB

4 小结

本文提出了一种针对噪声相关性影响下的自适应处理方法，该方法在基于子空间维度估计的主模式抑制处理的基础上，引入了具有去相关作用的子阵平滑处理，构成了新的自适应算法——子阵平滑主模式抑制(SS-NDMR)波束形成方法，该方法实现简单且有效。由于采用了分子阵平滑处理，计算复杂度相比于NDMR和MVDR均有所下降，其性能仿真和数据模拟仿真分析结果初步表明，对于有色高斯噪声背景，SS-NDMR方法比常见的自适应算法的检测性能更优。然而，本文并未对子阵维度及平滑处理的参数等进行更细致的讨论。

[1] MESSERSCHMITT T R, GRAMANN R A. Evaluation of the dominant mode rejection beamformer using reduced integration times[J]. IEEE Journal of Oceanic Engineering, 1997, 22(2): 385-392.

[2] NADAKUDITI R R, EDELMAN A. Sample eigenvalue based detection of high-dimensional signals in white noise using relatively few samples[J]. IEEE Transactions on Signal Processing, 2008, 56(7): 2625-2638.

[3] 邵鹏飞, 祝献, 王青翠. 基于子空间维数检测的主模抑制波束形成[C]//2016’中国西部声学学术交流会论文集, 2016.

SHAO Pengfei, ZHU Xian, WANG Qingcui. Dominant mode re-jection beamformer method based on subspace dimension detec-tion[C]//Proceedings of the 2016’acoustics conference of western China, 2016.

[4] WAGE K E, BUCK J R. Snapshot performance of the dominant mode rejection beamformer[J]. IEEE Journal of Oceanic Engineering, 2004, 39(2): 212-225.

[5] BUCK J R, WAGE K E. A random matrix theory model for the dominant mode rejection beamformer notch depth[J]. IEEE Statistical Signal Processing Workshop, 2012, 820-823.

[6] WAGE K E, BUCK J R. Performance analysis of dominant mode rejection beamforming[C]//Proceedings of 20th International Congress on Acoustics, ICA 2010: 1-6

[7] 牛潇, 王忠庆. 带有噪声相关性的自适应噪声抵消系统仿真研究[J]. 电子测试, 2010(7): 15-18.

NIU Xiao, WANG Zhongqing. Emulational research of adaptive noise canceller analysiswith noise correlation[J]. Electronic Test, 2010(7): 15:18

[8] 夏光荣, 刘兴钊. 相关性噪声对MUSIC算法参数估计性能影响的分析[J]. 电子测量与仪器学报, 2005, 19(4): 6-11.

XIA Guangrong LIU Xingzhao. Analysis of the performance of music algorithm in correlated noise[J]. Journal of Electronic Measuremant ans Instrument, 2005, 19(4): 6-11.

[9] 王珽, 张剑云. 色高斯噪声背景下相干信源DOA估计[J]. 航天电子对抗, 2012, 28(4): 32-35.

WANG Ting, ZHANG Jianyun. DOA estimation of coherent signals in color Gaussian noise[J]. Aerospace Electronic Warfare, 2012, 28(4): 32-35.

[10] 张纯, 杨俊安, 叶丰. 高斯色噪声背景下的单通道信源数目估计算法[J]. 信号处理, 2012, 28(7): 994-999.

ZHANG Chun, YANG Jun’an, YE Feng. Single channel source number estimation algorithm under colored Gaussian noise[J]. Signal Processing, 2012, 28(7): 994-999.

[11] 武思军, 张锦中. 基于协方差矩阵的空间平滑解相干算法[J]. 应用科技, 2005, 32(5): 7-9.

WU Sijun, ZHANG Jinzhong. An improved spatial smoothing technique based on covariance matrix[J]. Applied Science and Technology, 2005, 32(5): 7-9.

[12] 蔡晶晶, 宗汝, 蔡辉. 基于空域平滑稀疏重构的DOA估计算法[J]. 电子与信息学报, 2016, 38(1): 168-173.

CAI Jingjing, ZONG Ru, CAI Hui. DOA estimation via sparse representation of the smoothed array covariance matrix[J]. Journal of Electronics & Information Technology, 2016, 38(1): 168-173.

[13] 张林让, 廖桂生. 利用空间平滑提高小快拍数时的自适应波束形成性能[J]. 西安电子科技大学学报, 1997, 24(S1): 133-139.

ZHANG Linrang, LIAO Guisheng, BAO Zheng. Improvement of the performance of adaptive beamforming with a small number of snapshots via spatial smoothing[J]. Journal of Xidian University, 1997, 24(S1): 133-139.

[14] SHAN T J, WAX M, KAILATH T. On spatial smoothing for direction-of-arrival estimation of coherent signals[J]. IEEE Transactions on Acoustics Speech & Signal Processing, 1985, 33(4): 806-811.

Subarray smoothing DMR beamforming under the background of colored Gaussian noise

SHAO Peng-fei, ZOU Li-na

(Science and Technology on Sonar Laboratory, Hangzhou Applied Acoustics Research Institute, Hangzhou 310012, Zhejiang, China)

The actual ocean waveguide is a fading channel with space-time correlation, where the background noise field is characterized by non-uniform anisotropy and the space-time correlation of noise field is not a δ-function, all these factors greatly affect the detection performance of large aperture sonar. In this paper, the background noise is modeled as a colored Gaussian stochastic process, and the algorithm of dominant mode rejection (DMR) beamforming based on sub-array smoothing is designed to realize the adaptive processing with the function of de-correlation under the condition of small snapshot number and to improve the detection ability of large aperture sonar in colored Gaussian noise background. The simulation results show that the method has good ability to suppress colored Gaussian noise.

Gaussian colored noise; subarray smoothing(SS); dominant mode rejection(DMR); beamforming

TN911.7

A

1000-3630(2019)-01-0103-05

10.16300/j.cnki.1000-3630.2019.01.017

2018-01-06;

2018-03-02

国家海洋局海洋公益性项目(201305028)

邵鹏飞(1989－), 男, 湖北荆门人, 硕士, 工程师, 研究方向为水声工程。

邹丽娜,E-mail: 570384435@qq.com