基于芯片的DNA计算模型解决排课问题

胡 娟, 殷志祥 ,张丽丽

1 引 言

1994年, Adleman博士在Science上发表论文，首次用DNA计算成功地解决了有向Hamilton路问题[1],人类从此进入了借助DNA分子的生化反应来进行计算的崭新时代。此后DNA分子生物算法用它运算的高度并行性﹑大容量和低消耗帮助很多的学者解决了许多NP完全问题，1997年，Ouyang就利用分子生物学技术解决了图的最大团问题[2]，建立了一个与六顶点群整体相对应的DNA分子池，并进行了一系列的选择过程，这项工作证明了DNA计算具有解决NP完整搜索问题的能力。此后Paun G等在1998年，编著了《DNA Computing：New Computing Paradigms》,在此专著中就用Sticker模型很好的解决了NP问题集合的最小覆盖问题[3]，再一次证明了DNA计算NP问题能力。2000年Lila Kari等又用DNA计算很好地解决了限定邮路一致性问题[4]。

排课问题在高校教务管理系统中是一项重要又复杂的问题，早在1975年，N.L.Lawri,D.C.Wood和S.Even等人就证明了此问题为NP完全问题[5]，很多学者用各种方法来解决这个问题，如动态规划[6]、图像着色法[7-8]等。近些年来更多的学者用智能算法如粒子群算法﹑遗传算法[9]等作用于解决排课问题，也都取得了很好的效果。此后，研究DNA计算方法的学者也成功地将DNA计算很好地应用于解决排课问题。如2007年周康等给出了闭环DNA计算模型[10]；2012年殷志祥等给出了AcryditeTM分离技术DNA模型[11]；2014年单静怡﹑殷志祥给出了基于表面DNA计算模型解决排课问题[12]。本文在0-1规划问题[13]的基础上给出了一种基于芯片的DNA计算模型解决排课问题，并对模型进行了简要分析。

2 排课表问题与生物算法

排课表问题是涉及到教师﹑教室﹑班级﹑课程和时间的NP完全问题。其主要目标就是按照教学计划将教师﹑教室﹑班级﹑课程合理的安排在一周内某一个不发生冲突的时间里[14]。简单的排课问题与0-1规划问题的思想基本相同。本文在0-1规划的基础上，提出了基于芯片的DNA计算模型，在实验中，采用荧光标记技术，通过观察荧光将每次结果进行记录，通过比较，就可以得到需要解决问题的可行解[15]。

排课表问题有软约束和硬约束，怎样在所给定的约束条件下得出最优的排课表是我们需要解决的问题。

下面简单的构造一个排课表DNA计算模型。假设有4个班级需要3名教师，怎样用最少的课时排课。3名教师分别用t1,t2,t3表示，4个班级分别用s1,s2,s3,s4表示，2间教室分别用c1,c2表示，班级对应的上课情况为D=(dij) 如下：

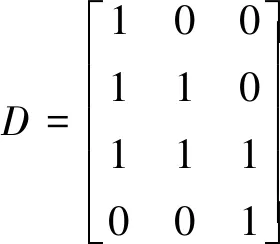
(1)

其中行表示为4个班级，列表示为3名教师，0表示这名教师在此班级没有课，1则表示有课。

这里我们给定一定的约束条件：一个班级在一个课时不能参加两门课的学习，一名教师在一个课时不能给两个班级上课。具体要求为：班级s4只能够在第二课时由教师t3上课，班级s1,s4只能够在c1教室上课，而班级s2却只能够在c2教室上课。

图1变量的编码图

图2所有课时情况芯片点样矩阵

生物算法：(1)对不同的变量生成相对应的DNA链，按照问题的要求，将一定量点样于事先已处理好的芯片上，用黄荧光对相应变量的补链进行标记。(2)将上述芯片与一定量变量的补链混合，由于补链会与其对应的变量相杂交并产生黄色荧光，由荧光成像技术就能找到符合问题要求的芯片点列。(3)加热表面，在严格条件下冲洗没有杂交上芯片，恢复其DNA链。(4)重复(2)、(3)，依次检验所有芯片点列(不再考虑已经符合要求的芯片点列)，分析每次的结果即可得满足约束条件的课时安排。

3 DNA计算的算法及其实现过程

3.1 编码

对于上面的实例，给定编码如下：

3.2 生物操作

3.2.1 由公式(1)班级上课的情况，将一定量的DNA链s1,s2,s3,s4, c1,c2点样于事先已处理好的芯片上(如图2)，列表示为教师t1,t2,t3给班级上课的情况，空为此教师在此班级没有课或此班级不限制在此教室上课。经过验证点样排列的矩阵是可以寻址的,因此方法是有效的。

3.2.2 先对第一课时进行选择，在这一循环过程中，我们分三步进行。

图3加入的杂交反应 图4加入的杂交反应

图5加入的杂交反应 图6加入的杂交反应

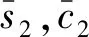
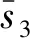
3.3 实验分析

从这一实验中得知，要想得到满足需要的课程安排，可由荧光颜色得到，结果如表1。

表1 课程安排

在此类排课表问题中，若dij≥2,即教师ti给班级sj至少需要上两节课时，可增加班级sj1,sj2,…,sjm，使m=dij-1,给D增加m行,使其仅含有0,1，即可用此模型来计算。

4 结论分析

文章对排课表这一数学中的NP完全问题，提出了一种基于DNA芯片的计算模型。该模型可以不改变所给问题的初始的点列，采用荧光标记技术，通过观察荧光将每次结果进行记录，通过比较，就可以得到需要解决问题的可行解。对于研究规模较大的问题简单方便。模型应用了DNA的芯片技术，能有效地解决更多此类问题，从而实现自动化。