目标跟踪滤波算法精度与可信性指标研究
2019-04-11王碧垚胡庄丽刘延峰
王碧垚 胡庄丽 廖 翔 刘延峰
(1.电子信息控制重点实验室 成都 610036;2.中国人民解放军东海舰队信息保障处 浙江 宁波 315000;3.中国人民解放军95438部队 成都 610100;4.西安电子工程研究所 西安 710100)
0 引言
目标跟踪即是利用单/多传感器所获得的量测对目标的运动状态进行持续地估计和预测,如图 1所示,跟踪算法的性能与航迹的起始、关联、滤波等性能都有关。在基于仿真或试验演练的跟踪滤波算法评估中,选取评估的参考信息为目标真实轨迹,则评估的核心就是基于指标体系分析跟踪滤波器输出的航迹与真实轨迹这两个时间序列之间的差异程度。
精度和可信性是估计算法评估中两个最基本最重要的指标[2]。目前精度评估中大多采用的指标是均方根误差(RMSE),Li[3]解释了具体原因并且分析了RMSE指标存在的缺陷,给出了其他非综合性指标以及误差谱(ES)等综合性指标,文献[4]将ES引入到动态系统评估中提出了动态误差谱 (DES),且推荐采用几何平均的计算形式。另外,估计器本身输出的均方误差(MSE)对于滤波过程中的增益计算至关重要,故度量估计器输出的MSE与真实MSE之间的差异也是很重要的工作,这被称作估计器的可信性度量(CM)[4],最早用于CM的指标是算术平均归一化误差(ANEES),但针对其存在的两大不足之处,文献[5-6]提出了新的指标,但计算时需要的真实MSE在实际中很难获取,从而降低了其工程实用性。
目标跟踪滤波器是估计算法用于实际工程的典范之一。本文将上述估计算法评估的思想引入到目标跟踪评估中,研究了跟踪滤波的精度和可信性指标的构建。针对精度评估中单一指标存在的缺陷,引入DES并将其与层次分析法(AHP)相结合,为权重确定给出了新思路,解决了精度综合评估问题。针对ANEES在可信性度量中存在的缺陷,给出了GANEES和HANESS的计算公式,提出了动态归一化误差平方谱(DNEESS)的定义以解决可信性的综合度量问题。通过仿真验证了所提指标的可用性以及优势。
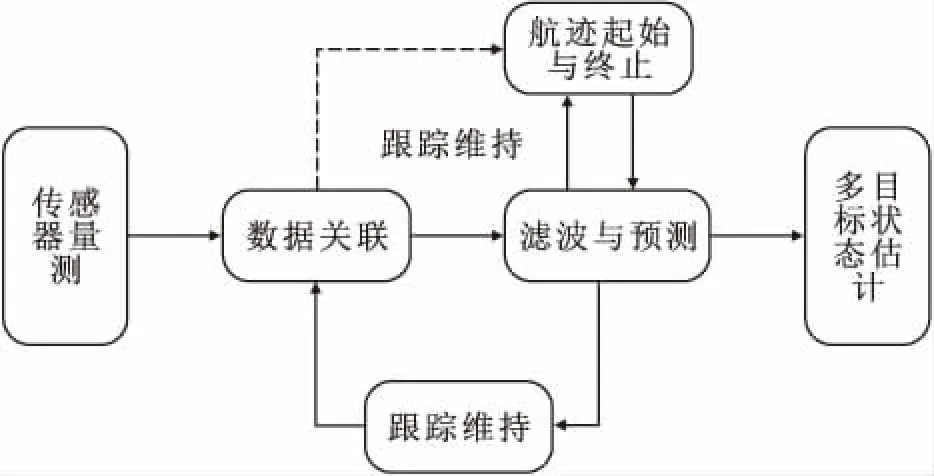
图1 基于数据关联的多目标跟踪方法原理图[1]
1 目标跟踪滤波评估概述
评估跟踪滤波器的性能时,通常是基于后验关联的思想,在跟踪过程结束后使用某种准则(如最大似然准则[7]),先对跟踪器输出的航迹与目标源真实轨迹间的归属关系进行配对,然后计算出各性能指标。对于仿真,目标真实状态已知,但工程实际中,目标的真实轨迹很难得到,一般是利用GPS数据或通过事后重构得到伪真实轨迹。文献[8]已给出了航迹归属关系判断方法及步骤,本文不再赘述。
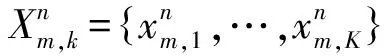
表1 符号约定

符号解释x真实轨迹或伪真实轨迹的变量x^x的估计值,如单传感器航迹状态或多传感融合航迹状态x~估计误差,即x~=x-x^‖p‖‖p‖=pTp()
2 航迹精度评估
2.1 非综合性指标
对于精度评估,滤波器输出的目标n的航迹在k时刻的均方根误差为:
(1)
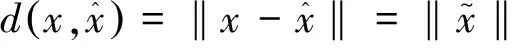
(2)
(3)
(4)
(5)
为便于计算,计算GAE时采用其对数形式:
(6)
其中,AEE虽也侧重反映较大误差样本,但不及RMSE严重。HAE侧重反映较小误差样本,GAE既不侧重较大误差样本也不侧重较小样本,是一个相对“公平”的指标。
考虑到航迹序列,给出这些指标的全局版计算公式,以AEE为例(另外3种很容易类比给出,不再赘述),其全局形式记为G-AEE,则有
(7)
2.2 综合性指标
由于非综合性指标会不公平地对待误差集中的部分样本,且从效能评估的角度考虑,总是期望用最少的指标对系统做出尽量全面的评价,这就有必要引入一种综合性指标对算法进行评估。很幸运,Li已经提出了ES和DES并给出了计算公式,但对于DES中各指标权重的确定没有给出有效的方法。
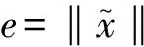
(8)
其中F(e),f(e)和pi分别表示e的分布函数,概率密度函数和概率质量函数。对于离散形式有[3]:
S(-1)=HAE,S(0)=GAE
S(1)=AEE,S(2)=RMSE
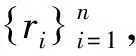
(9)
等权重时DES等价于Sk(ri)的算术平均值:
(10)
显然在评估中不是所有情况下都取等权重。因此,当根据评估意向选定ri所有取值后,本文引入AHP的指标权重计算方法确定各个分指标的权重。具体步骤为[9]:
1)确定指标权重标度
根据评估意向对指标进行两两比较,即重要性比较,得到量化的判断矩阵,引入1-9标度,见表2所示。
表2 AHP法指标权重标度

值意义1指标i与指标j同等重要3指标i略微比指标j重要5指标i比指标j重要7指标i明显比指标j重要9指标i绝对比指标j重要2,4,6,8是可以使用的其它中间值若指标指标i不如j重要,取值为1/v,v=1~9
令ai,j表示指标i相对于指标j的相对权重,则基于权重标度构造的判断矩阵为
(11)
2)指标权重计算与一致性检验
权重计算可归结为判断矩阵的特征向量和最大特征值的计算,步骤如下:
①计算判断矩阵A的行元素之积:
(12)
②计算Mi的n次方根:
(13)
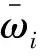
(14)
所求向量记为ω=[ω1,…,ωn]T。
④求解矩阵A的最大特征根λmax:
(15)
式中[Aω]i是Aω的第i个元素。
⑤检验矩阵A的一致性:
一致性用于评判构造出来的A是否可以接受。一致性指标(CI)和一致性比例(CR)作为衡量判断矩阵一致性的标准,规定CR<0.1时,矩阵可以接受,且CR越小矩阵一致性越好。当CR=0时判断矩阵是完全一致的。CI计算公式为:
(16)
当矩阵维数较大(≥3)时,CI修正为CR:
(17)
RI为修正因子,取值见表 3。当n<3时,判断矩阵很容易完全一致,不必计算CI。
表3 修正因子表

维数3456789RI0.580.961.121.241.321.411.45
3 航迹可信性度量
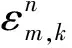
(18)
(19)
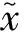
(20)
(21)
与精度评估一样,单一使用ANEES、GANEES或HANEES时存在片面性,只能侧重反映NEES样本集合中的部分信息,为充分挖掘样本集合中的信息,这里借助DES的思想提出DNEESS,有:
(22)
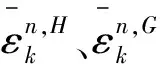
4 仿真实例
考虑杂波环境下机动单目标跟踪的场景,采用所提指标对两种算法进行对比(基于随机参数跳变马尔科夫的LMMSE算法和交互式多模型概率数据关联(IMMPDA)算法[11]),若为多目标场景,则计算结果对目标数再求平均值。

量测噪声服从零均值高斯白噪声分布且协方差为R=104×I2m2。跟踪器中的IMM模型包括CV和CA两种模型,状态转移阵
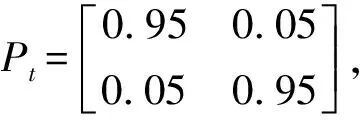
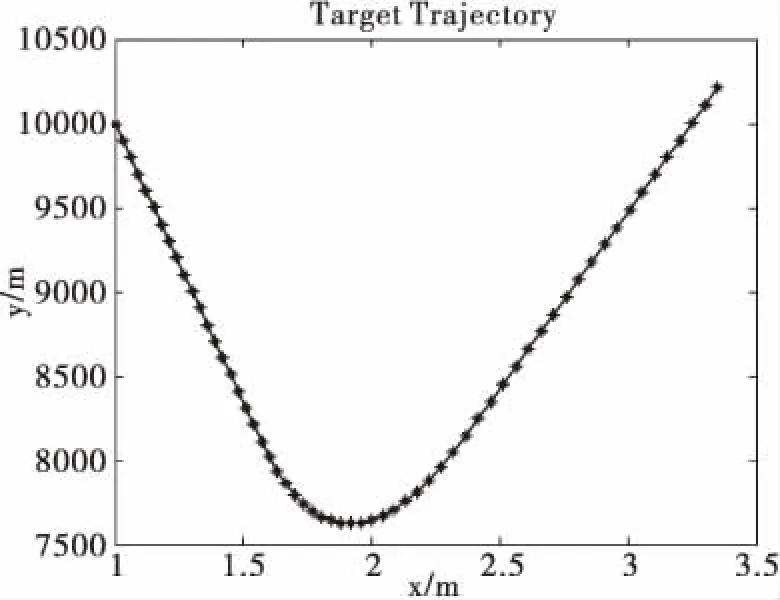
图2 目标运动轨迹图
精度评估分析:根据公式计算出四种位置误差指标,如表4所示,采用RMSE和AEE比较精度时,LMMSE算法优于IMMPDA算法,而用GAE和HAE比较时,LMMSE算法劣于IMMPDA算法。正是因为RMSE和AEE倾向反映少数过大误差样本,而HAE倾向反映少数过小误差样本,只比较RMSE是得不出这些结论的。
表4 IMMPDA和LMMSE算法精度比较
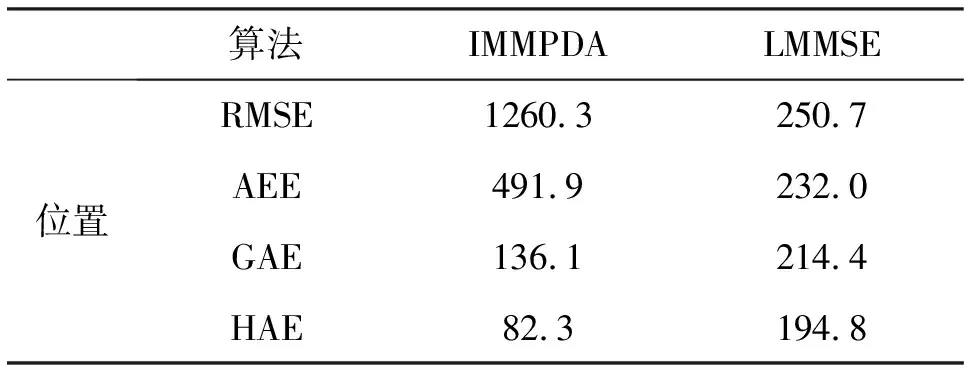
算法IMMPDALMMSE位置RMSE1260.3250.7AEE491.9232.0GAE136.1214.4HAE82.3194.8
取r={-1,0,1,2},采用节2中的方法根据不同评估目的建立不同的判断矩阵,确定三组权重不同的DES对两种算法进行评估,见表5。计算结果DES如图3所示:对比同种算法的不同DES值可知该算法的误差波动性,如图3表明IMMPDA的误差波动性较大,而LMMSE的较小,可认为LMMSE的稳定性优于IMMPDA;对比不同算法的同种DES,可从多种角度对比算法精度,如图3表明当侧重HAE和GAE(DES3)时,两种算法的精度很接近。 显然,DES相比单一的指标可以反映更多的误差样本信息。
表5 三组DES的权重和一致性比例
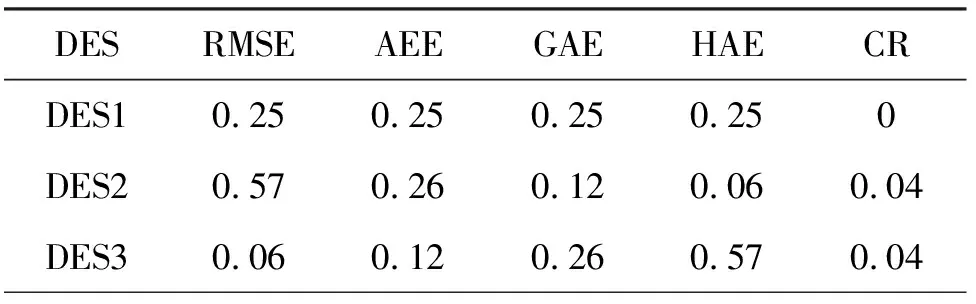
DESRMSEAEEGAEHAECRDES10.250.250.250.250DES20.570.260.120.060.04DES30.060.120.260.570.04
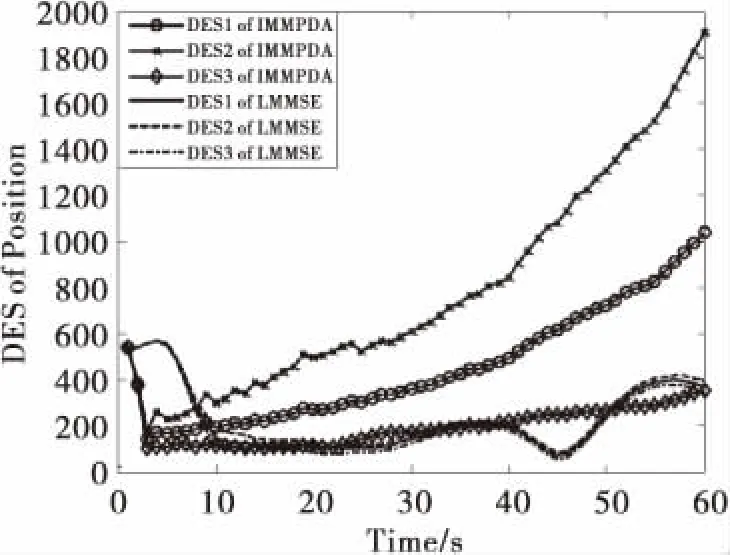
图3 两种算法的带不同权重的位置DES
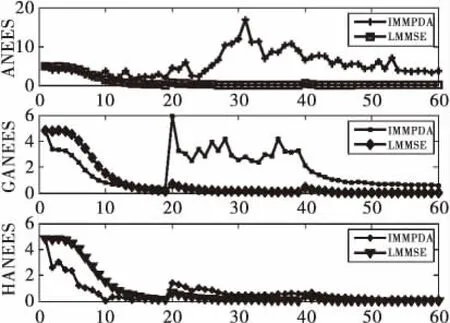
图4 基于三种指标的算法可信性比较图
表6 三组DNEESS的权重
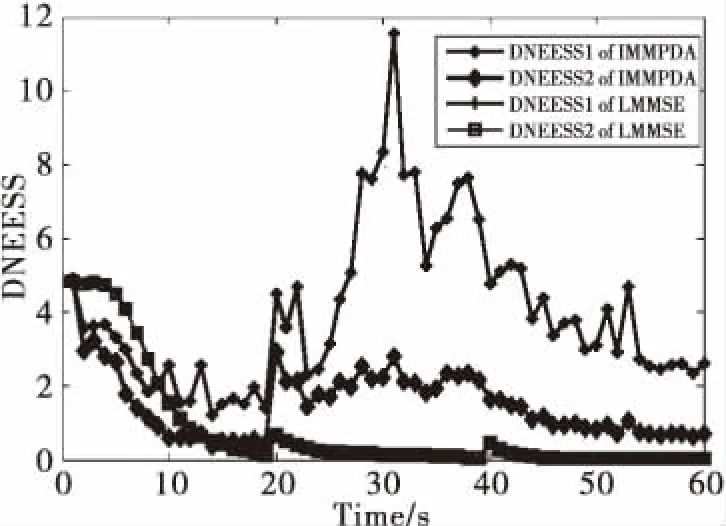
图5 两种算法的不同权重的DNEESS曲线图
5 结束语
本文在航迹-目标源已关联配对的前提下研究了精度和可信性指标的构建。考虑到精度评估中单一指标存在的缺陷,引入DES并将其与AHP法结合,为权重确定提出了新思路,解决了精度综合评估问题。针对ANEES在可信性度量中的缺陷,给出了GANEES和HANESS的计算公式,进而提出了DNEESS的定义以对可信性进行综合性的度量。仿真表明采用新指标进行评估时,可以挖掘误差样本集合中更多的信息。
