量子Fokker-Planck方程线性化算子的正则性与解的整体存在性

孙凤娇， 林春进

(河海大学 理学院， 江苏 南京 210098)

0 引言

本文主要讨论描述费米子的量子Fokker-Planck方程

∂tF+v·xF==·[F+vF(1-F)]

(1)

这里未知函数F(t,x,v)表示在时间t>0、空间x∈P3、速度v∈P3的费米子的分布函数，函数满足Pauli不相容原理，即0≤F(t,x,v)≤1；x和分别表示关于空间变量x和速度变量v的梯度.

若分布函数F与空间变量x无关，则相应的方程(1)称为空间齐次的非线性Fokker-Planck方程；若在方程(1)中忽略因式1-F，此时方程(1)是一个线性方程，即为经典的Fokker-Planck方程，描述的是Maxwell气体的分布函数；若在方程(1)中以1+F代替1-F，此时方程(1)则为描述玻色子的量子Fokker-Planck方程.由统计力学相关知识可知， Maxwell气体、费米子、玻色子的平衡态分别服从Gauss分布、Fermi-Dirac分布和Bose-Einstein分布.更多的物理背景可参考文献[1].

Carrillo等[2]应用相对熵方法讨论了量子Fokker-Planck方程的解收敛到相应的平衡态；Toscani[3]讨论了玻色子的量子Fokker-Planck方程的解的爆破，这类爆破对应了物理上的Bose-Einstein凝聚现象.

本文首先讨论方程(1)在Fermi-Dirac分布处的线性化算子的正则性.引入熵函数H(f)和熵积D(f)，并分别定义为

H(F)=

D(F)=

≥0.

可以验证F∞(v)是方程(1)的一个静态(空间齐次)解.

考虑方程(1)的解F(t,x,v)在Fermi-Dirac分布F∞(v)处的扰动：

(2)

代入方程(1)可得关于扰动f的方程

∂tf+v·xf=-L(f)+NL(f)

(3)

其中线性算子L(f)和非线性算子NL(f)分别为

L(f)=

(4)

到它的对偶空间V′上的有界线性算子，且L是自伴的.

由算子L的表达式知算子L满足：

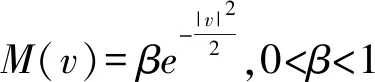
(5)

由基本不等式知

于是有

(6)

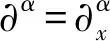
定理1存在常数C>0，使得对任意的f∈Ker(L)⊥∩V，都有

(7)

〈L(f),f〉V′,V≥C(f,f)

(8)

(9)

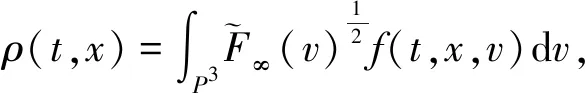
〈L(f),f〉V′,V=〈L((I-P0)f),(I-P0)f〉V′,V≥

(10)

这类不等式在动力学方程方面有着重要的作用.对于描述Maxwell气体分布函数的线性Fokker-Planck方程，其平衡态为Gauss分布，其正则性即为著名的对数Sobolev不等式[4-6].Degond等[7]讨论了Landau方程的关于Gauss分布处的线性算子的正则性.Lemou[8]进一步研究了带相对效应或量子效应的Landau方程的线性算子的正则性.关于Fokker-Planck方程和更多的动力学方程，可参考文献[9]；对数Sobolev不等式的推广可参考文献[10].

在线性算子L的正则性的结论下，可以证明描述费米子的Fokker-Planck方程在稳态解F∞(v)附近解的整体存在性.

扰动函数f(t,x,v)满足

(11)

动力学方程在平衡态附近光滑解的整体存在性，Guo[11]证明了周期区域上Landau方程中解的整体存在性，文献[12]得到了描述费米子的Landau-Fermi-Dirac方程解的存在性，文献[13,14]讨论了量子Fokker-Planck方程在周期区域上整体解的存在性，文献[15]中研究了一般化的量子Fokker-Planck方程以及自受引力粒子模型解的整体存在性，文献[16]得到了Vlasov-Fokker-Planck方程解的整体存在性.

本文借鉴了文献[16]中的技巧和文献[15]中的证明方法，引入扰动函数宏观量的估计，使一致先验估计更为直观.本文绕过对数Sobolev不等式，利用文献[8]中的方法证明算子L的正则性，利用文献[16]中的微宏观分解技巧，引入宏观量估计，获得了解的一致先验估计.

本文第1节，先给出定理1即线性算子的正则性的证明，其中命题1的证明放在第3节.在第2节，给出定理2 的证明.在以下的证明中，与f无关的常数都用字母C表示，且每一步中C可能都不相同.

1 线性算子的正则性

本节将证明定理1.

若f(v)∈Ker(L)⊥∩V，记

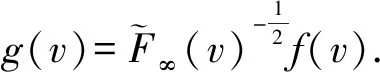
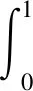
(1-t)y)dtdy，

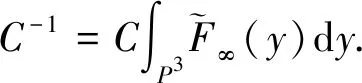
由Cauchy-Schwartz不等式得

(12)

其中C表示常数，函数ψ(x)为

ψ(x)=

对ψ(x)，有如下命题：

命题1存在常数C>0，使得

(13)

命题1的证明放在第3部分.利用命题1的估计式(13)，即得定理1.

2 扰动方程解的整体存在性

为了获得方程(3)解的局部存在性，首先要构造逼近解序列，并证明逼近解序列的一致能量估计.方法与Landau-Fermi-Dirac类似，可参考文献[12].在解的局部存在性基础上，需要更精细的一致先验估计，以及连续延拓技巧来证明解的整体存在性.解的一致先验估计是解的整体存在性的最关键的部分.本节主要讨论解的一致先验估计，首先给出能量泛函，然后证明能量泛函满足不等式.

2.1 预备知识

本节利用正交投影将扰动f分解为宏观部分和微观部分的和，最后给出能量泛函.

记P为L2(P3)到

f=P0f+P1f+(I-P)f,

其中P0f的表达式见(9)，

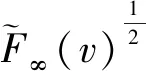
∂tρ+x·J=0

(14)

(15)

最后，给出能量泛函.自然数N=8，令

(16)

由正交投影，对任意的α,β

于是，利用三角不等式得

(17)

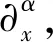
(18)

首先估计式(18)左端第二项.一方面由正交分解以及L的表达式，可得

另一方面由正则性，定理1，可得

于是式(18)左端第二项可以估计为

对右端非线性项，

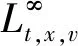
CN(T)3

(19)

综上，有如下估计：

C(N(0)2+N(T)3)

(20)

利用f的宏观和微观分解，方程(3)可写为：

∂t((I-P0)f)+v·x((I-P0)f)+

L((I-P0)f)=NL(f)-[∂t(P0f)+

v·x(P0f)]，

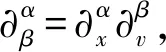
(21)

上式中，左端第2项由Cauchy-Schwartz不等式和Young不等式，可以估计为

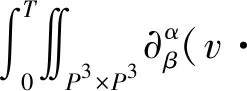
对于式(21)中左端第3项，利用文献[15]中的引理2.3可得

下面估计式(21)中的非线性项，即式(21)中右端第1项，与式(19)的估计类似，可得

此外，式(21)右端第2项可以估计为

对式(21)乘以适当的常数，再关于α,β求和，

|β|≥1,|α|+|β|≤N，并结合以上估计可以得到

(22)

2.4 ρ的估计

对式(15)两边关于x求α阶偏导，此处|α|≤N-1，再关于∂αxρ作内积，最后关于t∈[0,T]积分可得

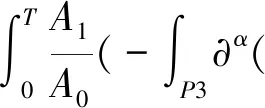
(23)

首先利用ρ,J满足的方程式(15)，式(23)左端项可估计为

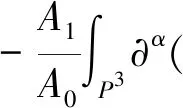
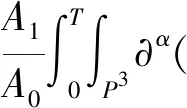
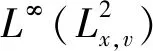
右端其余各项，由于只涉及关于x的导数，利用估计式(20)，都可以被下式控制

综上，对∀|α|≤N-1，有

N(T)4)

(24)

2.5 一致先验估计

由式(20)、(22)和(24)，得以下的一致先验估计

N(T)2≤C(N(0)2+N(T)3+N(T)4)

(25)

根据文献[12]、[16]或[17]，可得解的整体存在性，于是定理2获证.

3 命题1的证明

在证明ψ(x)的估计式(13)之前，先给出两个引理，它们在ψ(x)的分解式的估计中起着重要的作用.

引理1对任意的实数μ>0，都存在常数C(μ)，使得

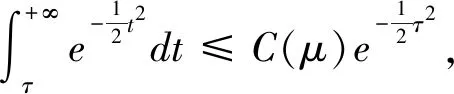
(26)

∀a∈[μ,+∞)

(27)

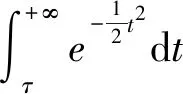
引理2若z<-1且z充分小，则

(28)

证明：对不等式左边积分换元，令

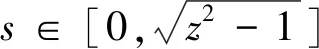
下面先化简ψ(x)，然后利用球坐标公式将拆分成三部分，再利用引理1、引理2分别给出相应的估计.

引入球坐标z=x+ρu，其中ρ>0，μ∈S2.令x·u=|x|cosθ.记τ=ρ+|x|cosθ，则ψ(x)的估计可以进一步化简为

(29)

利用θ的取值范围把上式右端拆成三项，即

ψ(x)≤C(ψ1(x)+ψ2(x)+ψ3(x)).

其中

(30)

(31)

(32)

C(1+|x|+|x|2)

(33)

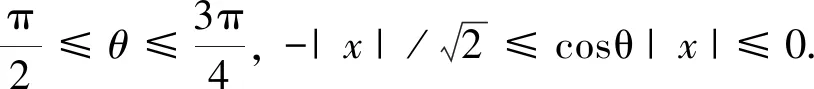
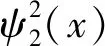
于是，得到

ψ2(x)≤C(1+|x|+|x|2+|x|3)

(34)

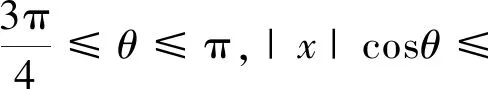
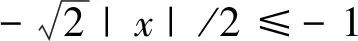
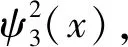
(35)

综合以上ψ1(x)、ψ2(x)、ψ3(x)的估计，可知存在常数A>0，使得对任意的|x|≥A，

ψ(x)≤C(1+|x|+|x|2+|x|3+

(36)

利用上式，只需要把命题1中式(13)P3上关于x的积分拆成关于|x|≥A和|x|≤A两部分，即可获得命题1的证明，具体的证明过程省略.

4 结论

本文主要考虑了描述费米子的非线性Fokker-Planck方程在它的一个平衡态，即Fermi-Dirac分布处的线性化方程正则性的问题，证明了线性化算子在其核空间的正交补空间上满足一个Poincaré类不等式，并在其正则性的基础上，证明了非线性Fokker-Planck方程的解在平衡态附近具有整体光滑解.