迅达电梯测试塔结构抗风设计
2019-04-10王晓亮WANGXiaoliang
■ 王晓亮 WANG Xiaoliang
1 概述
本工程位于上海市嘉定区工业园区内,地面粗糙度为B类。该建筑主要功能为超高层建筑高速电梯试验及自由落体试验使用,结构体系为钢筋混凝土筒体结构,其中,主体结构高约200.7m,平面呈正方形,外形尺寸为19.4m x19.4m,结构高宽比为10.34。由于结构为超高层建筑且极其细柔,根据《建筑结构荷载规范》(GB 50009—2012)和《高层建筑混凝土结构技术规程》(JGJ 3—2010),该建筑属于对风荷载敏感的高层建筑,不仅要考虑一般建筑中占主导影响的顺风向风荷载,还要考虑横风向风振和扭转风振,且结构的高度和高宽比均超出了规范适用的范围,该结构横风向的风致响应往往可能超过顺风向的响应[1], 抗风设计成为了该结构的主要课题。本文旨在提供一种抗风方案设计时的周期确定方法,通过对比规范提供的方法计算与风洞试验的结果,总结矩形细柔高层建筑的设计要点和风振等效静荷载的取值方法。
2 结构自振周期范围的确定
2.1 横风向漩涡脱落共振
本工程在进行剪力墙结构设计时,除了要考虑抗震设计的因素,结构在风荷载作用下是否会产生共振也是高宽比较大的结构方案设计时需要考虑的重要因素。大高宽比的柔性结构容易在横风向产生很大的动力响应,所以方案阶段需要大致确定本结构的自振周期范围。
由于本工程雷诺数Re=69 000vDR=8.1x107>3.5x106,风振处于跨临界范围,在此范围内的风振动特征为有规则的周期性漩涡脱落,属于容易引发强风共振的范围。风力作用下的漩涡脱落周期是决定结构是否发生横向共振的另一关键因素[2],为了避免结构发生漩涡脱落产生的横向共振,首先要确定漩涡脱落周期:

式中,B—结构垂直于风流速方向的最大截面尺寸。
根据文献[3]的试验分析结果,本工程正方形截面取斯脱罗哈数St=0.1;平均风速v取结构顶部风速vH,根据《建筑结构荷载规范》(GB 50009—2012)中的计算公式计算:
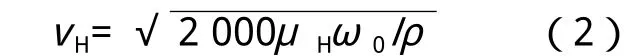
式中, μH—风压高度变化系数;
ρ—上海地区空气密度,取1.25kg/m3。
由此可计算出:在基本风压0.4kPa、0.55kPa和 0.6kPa下,Ts分别为4.85s、4.17s和3.99s。
此外,若结构的临界风速vcr小于1.2倍的结构顶部风速vH时,依然可能发生跨临界强风共振。考虑高层结构振动反应最卓越的第一振型周期T1作为控制周期,可以得到下式:
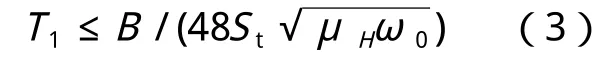
以上海地区10年重现期,50年重现期和100年重现期对应的基本风压0.4、0.55和0.6为控制计算,则第一振型周期分别不得大于4.08s、3.48s和 3.3s。
2.2 场地的卓越周期
对于自身基本周期较长的高层结构,地面运动的速度和位移可能比加速度对结构的破坏具有更大的影响。由于上海软土地层,土层的强烈非线性反应使得地表处反应谱的特征周期比小震时伸长较多。上海大部分场地的地运动卓越周期在2.0~2.4s,本工程通过场地的波速试验,得到场地卓越周期为2.09s。根据高度和长细比判断,如果将本工程结构的第一阶自振周期控制在2.09s之内费用太大,非常不经济,所以应该控制第一阶自振周期大于2.09s。
2.3 综合分析确定结构周期
综合上述分析,得出本工程结构避免共振的一个安全频段(图1),其两个主轴方向第一周期的合理范围应控制在2.09~3.3s之间,同时也可以看到,按照跨临界风振的界限周期控制,可以较远地避开漩涡脱落周期。
通过结构剪力墙布置调整后,外墙墙厚为700mm,x方向第一周期为3.2s,y方向第一周期为3.18s,第一阶扭转周期为0.71s。其底部标准层平面布置如图2所示。
暂时不考虑超高的因素,以基本风压0.6kPa为例,按照荷载规范的算法对比第一阶自振周期T1为4s和3.2s的横风向风振等效荷载(图3)发现,T1=4s的等效静力比T1=3.2的等效静力明显增大,最大位置出现在楼最高处,增大比例达到1.55倍。
3 试验工程概况及主要结果
3.1 概况
该高层建筑风洞试验在同济大学TJ-2大气边界层风洞中进行(图4)。风洞试验段为3m宽、2.5m高的矩形截面,试验类型为刚性模型测压试验,主要测量系统采用DSM3400电子式压力扫描阀系统。基本风压及梯度风速度(10年重现期)0.40kPa,基本风压及梯度风速度(100年重现期)0.60kPa;阻尼比取0.05,舒适度分析时取0.02,参振模态取1~15阶。
风从建筑东方(地理方位北偏西30°)吹向本工程时定义为0°风向角(x方向),风向角按顺时针方向增加。试验风向角间隔取为15°,在建筑西北方向(即风向角345°至15°)风向角加密到间隔为2°,这样共有35个试验工况。方位及风向角定义见图5。
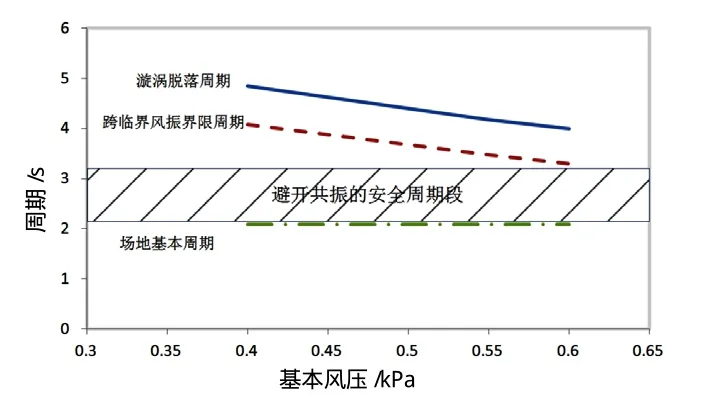
图1 安全周期段示意图
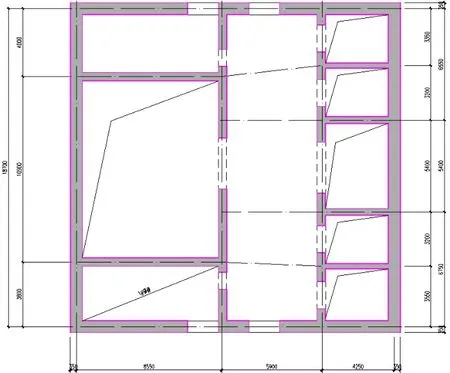
图2 标准层平面图
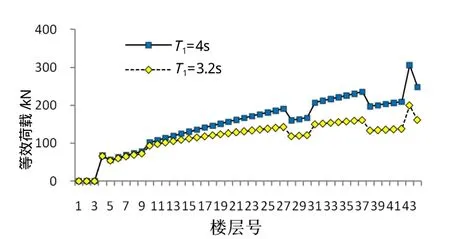
图3 横风向等效静力对比

图4 风洞试验模型照片
3.2 加速度及位移变化
从顶层加速度变化图(图6)发现,加速度峰值分别出现在0°,90°,180°,270°和360°,可见顺风向风荷在产生的加速度占主导地位。顺风向加速度出现峰值时,横风向加速度虽然也出现极值,但只有顺风向的0.6~0.7倍。顶部加速度最大值为0.245m/s2,未超过规范限制的0.25m/s2。
从顶层位移曲线图(图7)可以看到,顺风和横风向位移峰值均出现在0°、90°、180°、270°和360°,且横风向风振产生的位移略大于顺风向位移。最大总位移为0.159m。
3.3 结构基底内力
图8~10为风洞试验得出的结构基底内力。由于本工程结构平面为正方形,所以基底剪力、弯矩仅给出x方向的结果。
从图8、9中可以发现,基底剪力和弯矩的峰值均出现在风向与建筑物正交的时刻。0°风向产生的x方向基底内力与90°风向产生的x方向基底内力相比,不论是剪力还是弯矩,最大绝对值均由横风向产生,且横风向风振产生的基底内力最大值约为顺风风振产生的基底内力的2倍。
从图10的基底扭矩结果可见,扭矩峰值均出现在风向与建筑物程15°方向,且相对于基底弯矩,结构在风作用下的扭转效应较小。
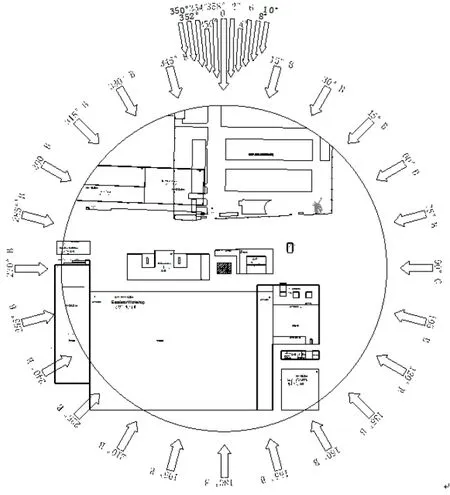
图5 项目方位及风向角定义
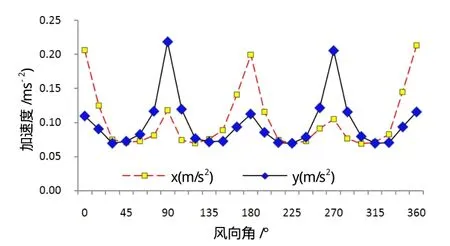
图6 顶层顺风向和横风向加速度变化图
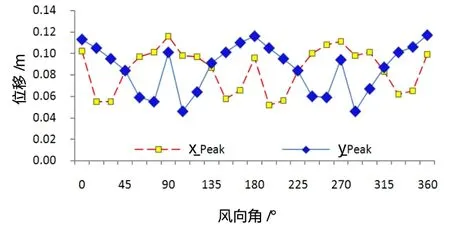
图7 顶层顺风向和横风向位移曲线图
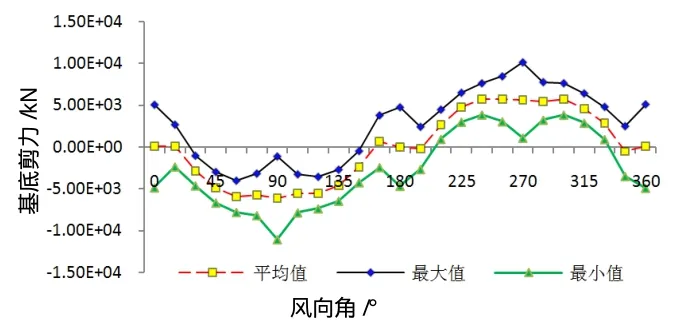
图8 x向基底剪力(Qx)图
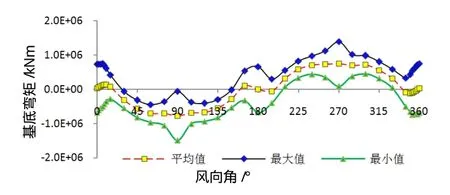
图9 x向基底弯矩(My)图
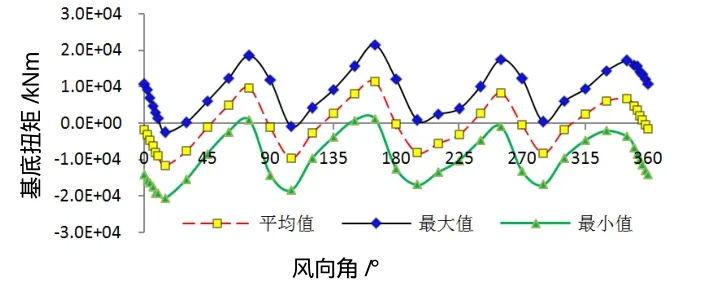
图10 基底扭矩(Mz)图
4 等效静力风荷载
为了用于结构设计软件的输入,风洞试验报告提供了考虑多模态贡献、满足各层内力、位移动力响应等效的多模态综合等效惯性风荷载,通过与试验得到的平均风压相加(或相减),得到绝对值,即得到了结构响应峰值的等效静力风荷载及。由上文的基底内力结果分析,横风向荷载效应大于顺风向,所以风洞试验得到的两个主轴方向的等效静力均来自于横风向风振。本节将风洞试验的等效静力风荷载与采用规范方法计算的等效静力风荷载进行了对比。
顺风向等效静力风荷载应考虑脉动风压对结构产生的风振。由于本工程结构的迎风面宽度远小于其高度,笔者认为,计算背景分量因子Bz时,应该按照高耸结构取值。规范方法和风洞试验得到的对比如图11所示,两种方法得到的等效静力基本相同,且规范方法可以较好地包络风洞试验结果。
横风向等效静力风荷载按照荷载规范计算时,横风向共振因子与无纲量横风向广义风力功率谱SFL有关,但是规范只是根据高宽比H/6计算了各地貌的功率谱图,适用范围在H/~8之间,所以按照规范方法的计算值明显小于风洞试验的对应值对于本工程,如果按照规范方法获取横风向共振因子RL,则需要将计算得到的横风振等效风荷载标准值提高至1.7倍,方可较好得包络风洞试验结果的等效静力荷载(图12)。
由图13可以发现,对于扭转等效静力风荷载,按规范方法计算得到的等效静力扭矩在顶层与试验结果比较相近,但在其余各层偏低于试验结果。等者认为,造成这一偏差的主要原因依然是结构高宽比超出了规范的适用范围。针对本工程,笔者结合风洞试验结果,将相关规范中计算式进行了修正:
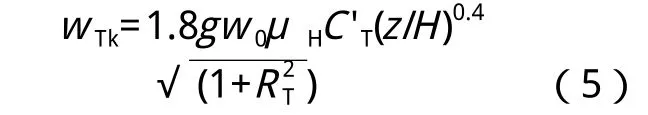
式中,C "T—风致扭矩系数;
μH—结构顶部风压高度变化系数;
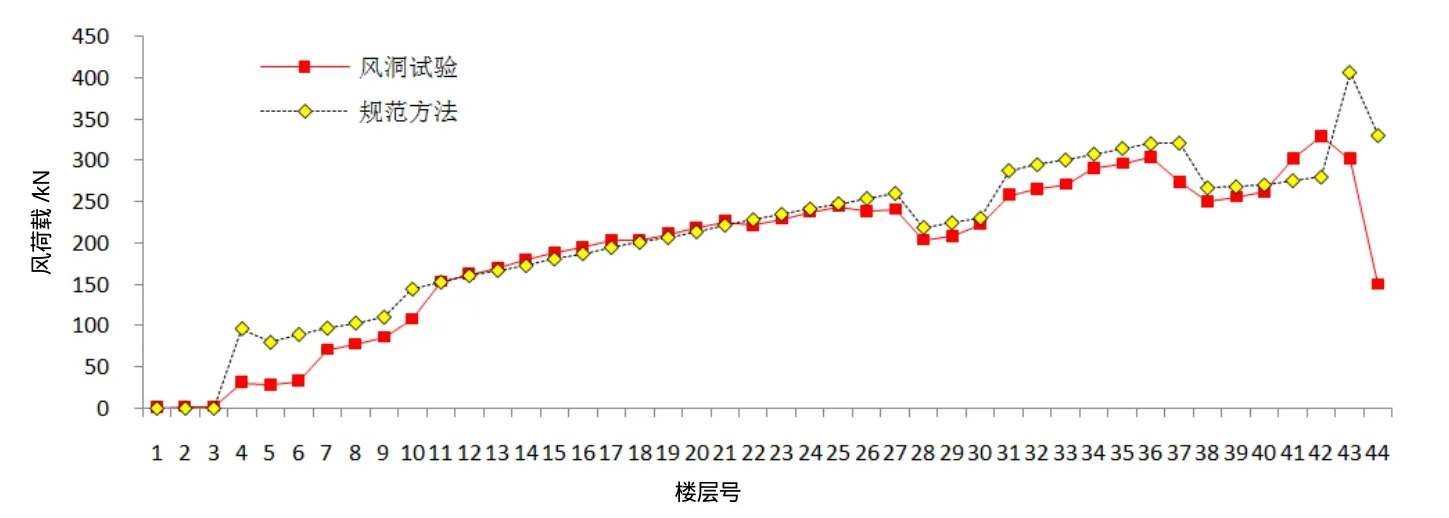
图11 顺风向等效静力风荷载
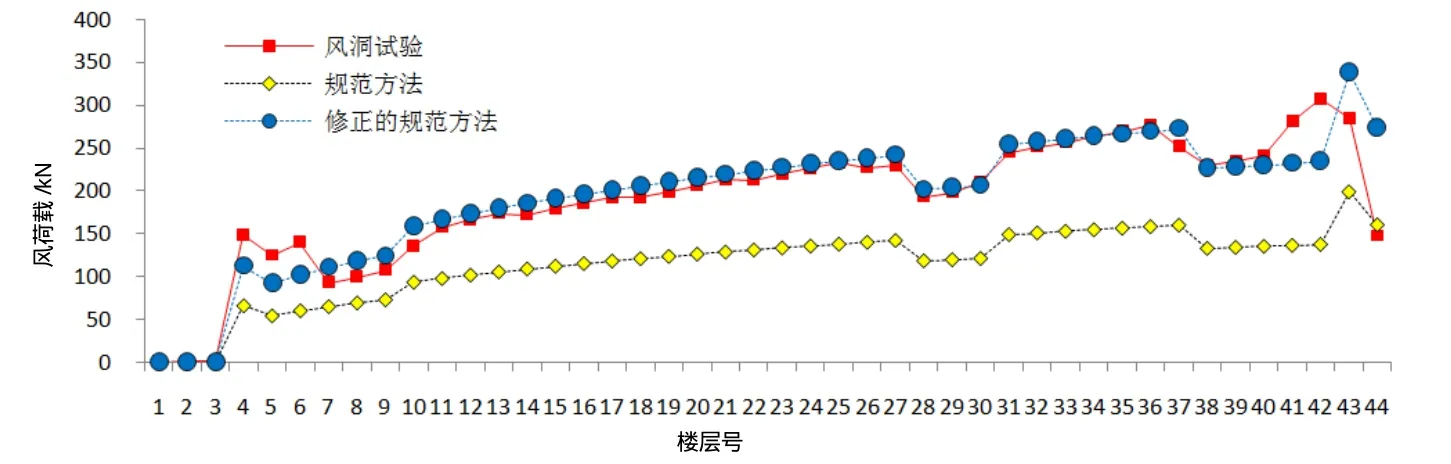
图12 横风向等效静力风荷载
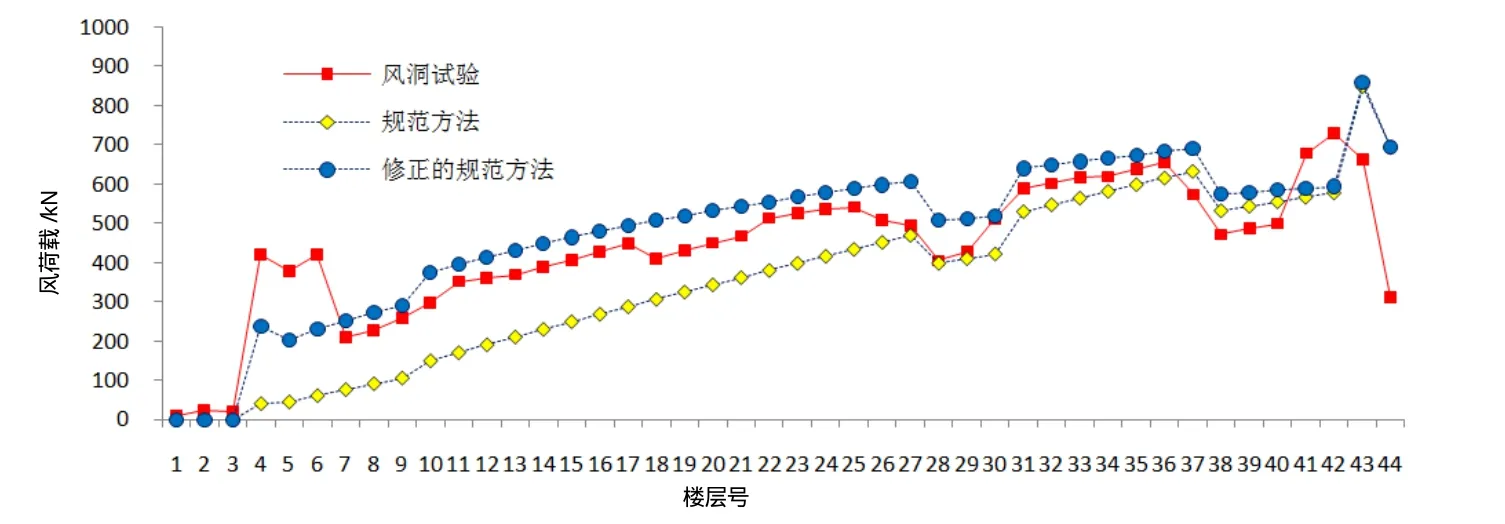
图13 扭转等效静力风荷载
g—峰值因子,取2.5;
RT—扭转共振因子。
可以看出,修正后的各层等效静力扭矩可以较好地包络风洞试验结果的等效静力荷载。
5 结论与展望
(1)通过对结构的第一阶自振周期控制,避开容易产生共振影响的频段,可以大大减小结构横风向的风振效应。
(2)经过风洞试验验证结构方案,结构的加速度指标满足舒适度要求,且在风荷载作用下未出现显著的顺风向或横风向共振效应,结构方案合理。
(3)经过对比风洞试验和规范方法计算的等效静力荷载,对于在B类粗糙地形条件下的截面接近正方形且高宽比为10左右的高层建筑,顺风向等效静荷载可以采用规范计算方法确定,但是横风和扭转等效风荷载会随着长细比增大明显提高,可以采用本文提出的修正的规范方法进行计算。
