基于后悔理论的城市轨道交通乘客路径选择

江妍妮，杨聚芬 （上海工程技术大学，上海 201620）

0 引言

随着城市发展规模不断扩大，城区面积逐渐向四面八方延伸，轨道交通的网络化结构成为城市交通的必备条件。当乘客在出行过程中确定了出发地和目的地之后，线网中可以选择路径不仅仅只有一条，往往存在多条路径。随机效用最大化理论普遍被应用于出行者的路径选择问题中，孙鸾英[1]等人认为随机网络加载模型就是利用随机效用最大化来计算各条路径的阻抗，从而决定出行者选择；龙学琴[2]等人引入了机会成本应用于后悔理论中，结合每条路径的预测出行时间和机会成本，出行者做出最终的选择；李梦甜[3]等人引入了无差异曲线的时间剩余概念和后悔理论结合，建立了基于时间剩余的出行时间和出行费用双重费用下的随机后悔最小化理论；闫祯祯[4]等人，构建了出行者在选择前获取信息时，基于期望后悔效用差别的交通信息感知价值模型，从而得到不同的路径选择；Chorus[5]等人基于后悔思想描述了出行者获取信息和出行决策的过程，并构建了随机后悔最小化模型。本文只考虑到自由出行者的路径选择，因为路径的选择相对通勤者不固定，多样化。通过分析影响出行者路径选择的主要因素，将随机后悔最小化理论与随机效用最大化理论结合，构建模拟路网，计算出路径的选择概率。

1 乘客出行影响因素

1.1 出行者乘车时间。乘车时间包括列车的区间行驶时间和停站时间，与乘客属性无关，但是控制中心可以通过实时线网的客流分布情况，来判断当前的列车行驶速度和停站时间是否满足客流需求。

公式中，Tc为乘车时间；∑tp为列车在乘客选择路径中所有区间的运行时间之和；∑ts为乘客选择路径中所有车站的停站时间之和。

1.2 出行者换乘次数（随机加载网络）。轨道交通线网中的换乘次数越多，乘客的心理感知费用也会增加，因此，换乘时间是对每次换乘时间依次进行放大得到的时间。表示为：

其中，nk,rs表示路段rs间路径k上的换乘次数，β为待定参数，根据实际交通流分配模型，β=2时较接近实际[5]。

2 后悔理论及其属性影响下的路径选择决策

2.1 后悔理论与路径选择的结合。在经济学中，后悔理论是指当一个人面对两种或多个选择情况时，不同的选择方案有各自的属性值，在选择的过程中，不但要考虑期望选择方案的表现如何，还要兼顾其他选择方案。后悔理论假定个体对选择方案的偏好依赖于可以选择的其他选项，即可以替代的选择。其中，定义后悔理论效用函数为（U x,y，x）表示个体可以获得的收益，y表示放弃选择产生的结果。即使x的增加会使总体效用更高，但随着y的增加，个体会因为被放弃的方案而感到越来越失望懊悔。

同样的情况，应用到轨道交通出行者路径选择的问题中来，出行者心中有一条期望选择路径，但同时还有多条路径可供选择，那么，根据以上的后悔理论，认为由本文路径选择的属性包括乘车时间t带来的个体收益为Vt，换乘次数带来的收益为Vn；在实际情况中，当出行者偏好较短的乘车时间，那么则必须接受由更多次换乘带来的负面收益，并且会因为换乘次数的增加而越来越感到失望，总体的效用也会因此降低。

在图1中，后悔效用函数的斜率随着x和y之差的增大而增大。两种属性的效用值相差越大，出行者将越感觉后悔失望[5]。

换句话说，后悔理论假定了个人期望选择，当选择方案的效用值小于未选择的其中一个或几个，那么就认为是后悔的；反之，当选择方案的效用值大于未选择的，则认为是愉快的。对m条路径N1,N2,…,Nm，根据出行者感知效用，后悔—欣喜函数可以表示为：R[v（xi）-v（x*）]。其中，xi表示选择路径Ni时，v（xi）表示选项xi的效用值，v（x*）表示其他未选选项的效用值最大的一项。则当R＞0，欣喜；R＜0，后悔。

图1 后悔效用函数

在针对如何做出选择这一方面，需要明确每一种选择方案的选择概率，即对选择和未选的。因此，便引出每个选择路径的期望后悔（ER），并且结合概率来衡量该选择。当一个选择方案满足∑ [P（s）*Rij（s）]＞0时，根据后悔理论，该选择方案会给出行者带来欣喜的结果。其中，P（s）代表选择路径i时的概率，Rij（s）表示后悔值或是欣喜值，当取后悔值时为负数，即其中一个未选路径j的效用高于选择方案i；取欣喜值时则相反。当且仅当所有的加和数值为正数时，对于选择路径i才不会产生后悔。

因此，需要明确P（s）和Rij（s），具体方法如下，有三条备选路径，i,j,k，影响选择的属性因素分别是x（乘车时间），y（换乘次数），z（其他）。

其中，φx,φy,φz为属性后悔函数，是根据效用最大化计算得出，即：

其中，β是可取值的参数，代表不同影响因素的重要程度[6]。

2.2 折中效应。当出行者有多条路径可供选择时，出行者往往会针对每个可选路径的各个属性，包括乘车时间、换乘次数、换乘时间、舒适度等因素，分别比较各自的效用，按照效用值的大小进行排序，最后取中间值所对应的路径，即为出行者最终的选择。在这些因素中，效用在某一个属性值表现最好并不会成为出行者的第一选择。可以理解为，在轨道交通出行者路径选择时，对自由出行者而言，较短的乘车时间必定是以其他属性的效用为代价来换取的。

事实上，在实际线网中，我们无法找到一条十全十美的路径，使之满足其各个属性达到一个完美的值，这也是为什么要经过理论分析，来找到一条相对完美的路径供出行者参考。

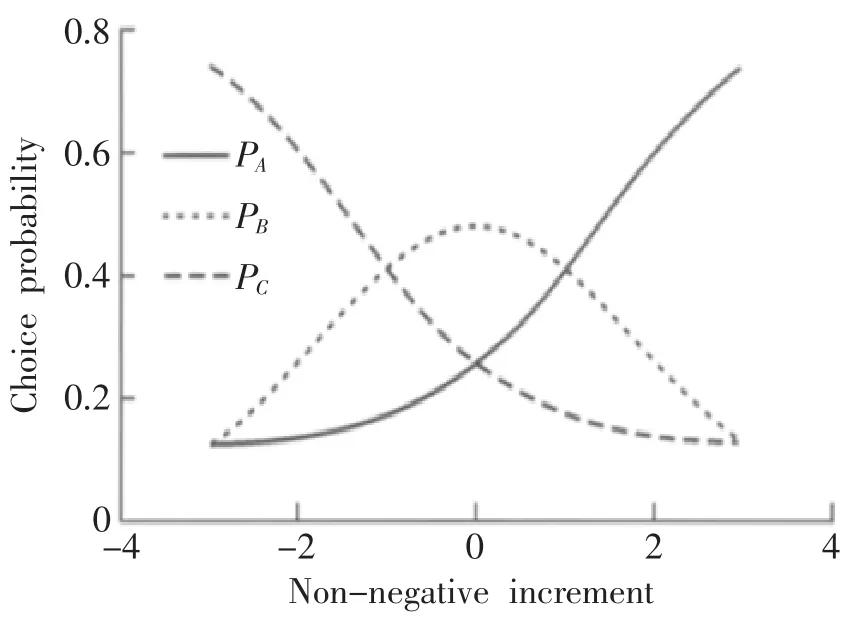
图2 属性值—概率变化示意图

如图2所示，根据轨道交通出行者路径选择的相关参数及属性，可以同样将此图应用于此。A、B、C表示三条可供选择的路径，每条路径都有两个同等重要的影响因素，即属性值；横坐标代表相关属性值的增量，纵坐标代表选择的概率，三条曲线则代表随着属性值的增加，出行者选择概率的变化情况。其中，PA和PC分别属于两种极端情况，即某一个属性值非常高，而另一个又很低；PB则介于二者之间，没有突出的属性值。

针对出行者如何选择的情况下，我们不能一概认为所有的出行者都会折中选择路径，而实际出行中，每个出行者的个人偏好不同，期望与实际的相差值也不同，因此折中效应只能作为一个参考的中值点来衡量，不能够做最终的判断。

在折中效应的影响下，可以看出，当属性的增量为0时，路径B的选择概率明显高于其他两条，也就是说，在某一稳定的状态下，所有路径的各个属性保持不变，属性值表现居中选项的选择概率最高。

2.3 半补偿效应。在效用最大化模型中，当一条选择路径因自身的一个属性值降低而整体改变时，出行者选择概率将完全被另一个属性值的对应增加而补偿，这是完全补偿效应；而在后悔最小化模型中，属性值i优于属性j和l，但不如m，很显然的是，当l的增量少于m的减少量时，属性m的影响程度更明显。

2.4 情绪管理原则。在个体进行决策选择的过程中，一个决定是否引起后悔或欣喜在一定程度上由其自身的情绪决定，所谓的负面情绪影响，是造成后悔值的主要原因之一。可以认为，个体在不同的情绪状态下，所定义的后悔临界值也不同，因此会在出行者路径选择过程中产生一定影响。

在轨道交通出行中，诸如列车车厢拥挤、换乘走行时间过长、设备故障引起的一系列影响运营的情况等无法控制的因素，都可以促成消极情绪的产生，也是引起出行者选择后悔的因素之一。

3 基于随机后悔最小化的出行者决策模型

3.1 随机后悔最小化（RRM）和随机效用最大化（RUM）的比较。RRM认为一个选择是否产生后悔取决于其他与之竞争的选择，而RUM则认为一个选择产生的效用仅仅依赖于该选择本身的属性。也就是说，RRM在各个选项路径中有相对竞争的关系时，会起到更好的作用；RUM仅仅是基于选项路径中自身的属性而发挥作用。另外，当其中的某个选项路径的大多数或全部属性值都优于其他的路径时，就存在一个最佳选择。若不存在这个最佳选项，则某一条路径的期望后悔就越大；反之则越小。可以作出如下的解释，即每条路径都存在竞争关系，无法找到那个最佳路径，就意味着在做出选择的时候犹豫不决，各条路径的属性值都有相对优越之处，也就无法分辨具体哪一条路径在整体属性的表现最优，在选择过后产生的后悔情绪也随之增加。

3.2 模拟路网建立。模拟路网示意图如图3所示，各条路径属性值如表1所示。

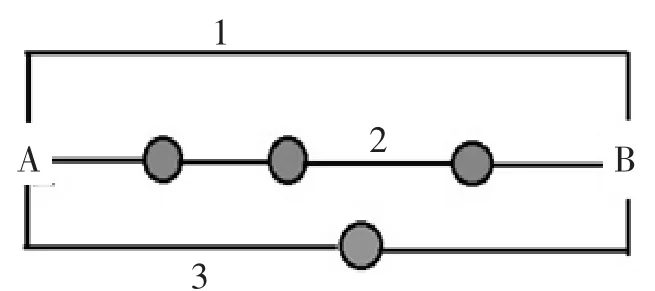
3.3 RRM模型及算例分析。对于本文中只考虑自由出行者的路径选择而言，根据前期的问卷调查，设置β在行车时间t因素中取-0.2，换乘次数n因素中取-0.7，且βt+βn+βx=1，其中βx表示其他因素。即自由出行者认为换乘次数在衡量过程中占主要考虑因素。同时，可根据 β 取值列出以下RRM模型进行计算：

因此可以得到每条路径相对其他两条路径的后悔值，分别在已选择和未选择两种情况下，如r12即为选择路径1的条件下，对路径2的后悔值。

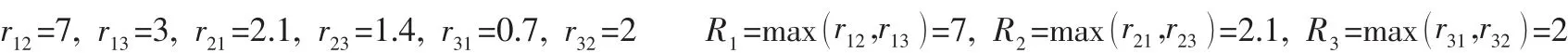
综上所述，根据RRM选择后悔值最小的路径，为路径3。因此可以得到如下结论，路径1的换乘次数虽然占优，但考虑到乘车时间，自由出行者的选择后悔值最高；而路径2的乘车时间虽然说最短的，但换乘次数是出行者考虑的主要因素，可见，两个因素都表现平平的路径3，在实际自由出行者的选择中，有较小的后悔值，这也正符合上文提及的RRM的折中效应，可以应用于实际路径选择。

4 研究小结

在面对多种选择情境下，出行者会权衡每一种选择路径的利弊，反映了出行者规避风险、降低心理后悔的意识；而对于最后决定选择的路径，出行者必将承担其可以接受的风险和后悔值，同时对于放弃的其他路径也要欣然接受。本文基于后悔理论，建立了三条不同类型的路径模型，分析了自由出行者在乘车时间和换乘次数两个属性的衡量之下，利用随机后悔最小化理论建立模型，并在其折中效应、半补偿效应和情绪管理原则的影响下，计算出每一条路径的理论后悔值。结果表明，当一条路径的各个属性表现平平，即整体性较好时，对于该条路径的后悔值越小，出行者更倾向选择；并且与效用理论相比，也解决了效用理论存在的绝对属性，即仅仅考虑一条路径本身的属性而不与其他选择作对比。然而，随着轨道交通线路的增多，备选路径数量也会随之增加，RRM中的变量会呈指数增长，使得计算变得非常复杂，在未来的研究中有待改善。