基于多运输渠道供应商最优订货的研究

张 鼎 （上海理工大学 管理学院，上海 200093）

0 引言

随着全球化的发展，世界开始形成地球村，越来越多的制造商和零售商选择其他供应商生产或者供应零部件。另外，更多的制造商为了节约成本，开始在全国甚至全球范围内选择生产供应地。例如，富士康给全球很多的企业生产零部件，三星企业给苹果公司生产零部件。尤其是汽车制造业，这种方式更为普见，像奔驰、大众等。文献[1]运用SWOT分析法，提出我国汽车零部件企业已经全面进入全球化采购的体系中。本文主要研究在多渠道情况下的供应链如何确定最优的订货政策。

近年来，有不少学者研究供应链中的最优订货量。例如，文献[2]研究多产品多库存的订货问题，发现随机需求下存在最优的订货决策。文献[3]提出一个利润优化模型，然后通过遗传算法来求得这个供应链中的优化问题。文献[4]使用报童模型探讨低碳供应链中的最优订货量，并考虑社会福利化最大化的问题。文献[5]通过使用经济批量法来求得最优订货量。文献[6]第二个贡献是有效的集成分支定界和交替方向乘法器（ADMM）算法，用于解决成本效益高的RDMPC问题。文献[7]在全球化的情况下，通过提出一种具有多目标优化的新型双层多级编程法来得到Stackelberg-Nash均衡以及最有利润解。

另外，文献[8]为了降低运输的成本和满足顾客的需求，通过一个较低成本的搜索算法来解决运输过程的总成本，实现供应商收益最大的目的。文献[9]关于需求，输入供应和路线可用性的不确定性通过使用两阶段随机程序的有限场景来建模，并得出最优的运输方式。文献[10]通过遗传算法解决了多式联运运输方式选择多目标优化问题的数学模型及虚拟运输网络图。文献[11]研究绿色供应链，提出一个网络层次分析理论ANP来克服各因素间的相关性。

然而，基于上文的研究结果，本文提出一个具有多种运输渠道的供应商，在接到订货量之后，如何确定自己最优的订货数量去生产；然后利用多运输渠道配送到市场以及从市场配送到顾客手里。总之，本文的问题可以描述为：考虑一个多产品供应商如何最优的订货数量以及最大化自身的利润函数。同时，通过算法的提出以及算例验证了本文模型的正确性和有效性。

1 模型建立与分析

1.1 基本假设

本文考虑一个供应商有多个生产地生产供应n种零部件。其中，每个零部件只能选择一个生产地进行生产。零部件从生产地生产好到顾客手中有两个阶段：零部件从生产地到市场和从市场到顾客手中。假设第一阶段的零部件有两种运输方式：路运和水运；第二阶段的零部件有两种方式：顾客自提和邮寄。另外，对于本文的供应商，有如下假设：供应商的同种零部件只供应一个市场；同种零部件只选择一种运输方式；同种零部件只能选择自提或者邮寄。

本文符号定义如表1所示：

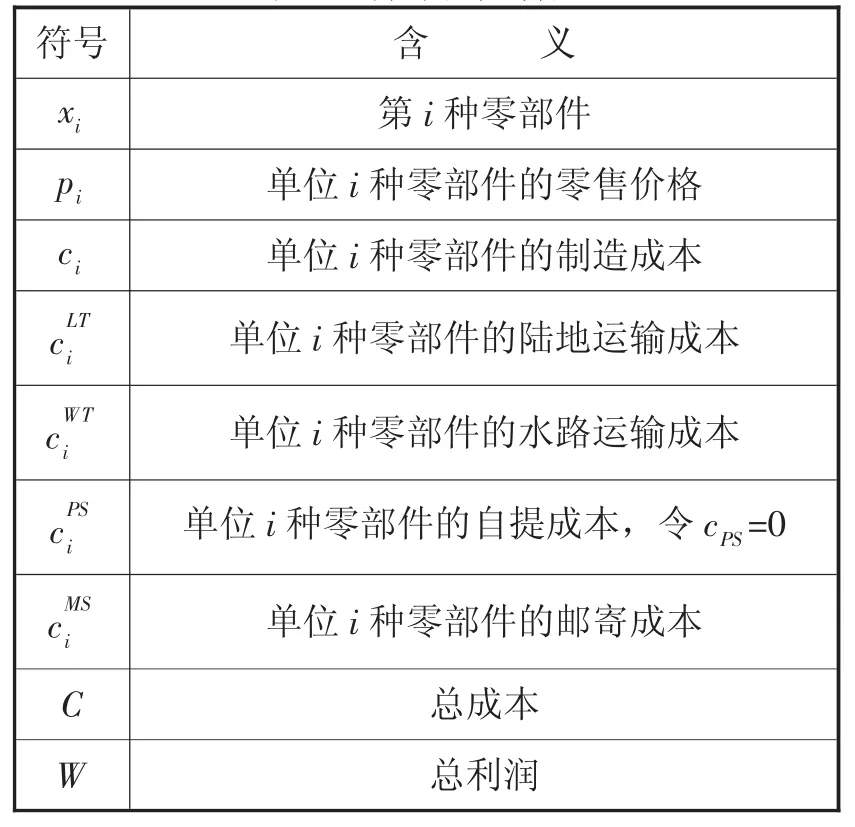
表1 符号及其含义

另外，本文有下面的二元变量：

对于供应商来说，决策问题是如何确定第i种零部件的订购生产数量，以及最大化的利润函数。其中，供应商的决策事件的顺序如下所示：首先，供应商了解市场的需求，获取并发送订单到生产地；生产地生产后，供应商选择最优的运输方式，陆地运输或者水路运输配送到市场；到达市场后，顾客选择自提或让供应商配送到顾客自己手中，供应商并收取自己的收益pi。这样，整个的决策过程就是一个优化的目标函数的过程。

1.2 模型的提出

首先，供应商的成本有着不同的组成结构，包括生产成本和运输成本。根据上文的分析，了解到供应商的决策问题以及需要求解的变量。因此，有下列总成本公式：

在式（4）中，第一项是供应商的生产成本；第二项是供应商从生产地配送到市场的陆地运输成本；第三项是供应商从生产地配送到市场的水路运输成本；最后一项是供应商从市场配送到顾客手中的成本。

同时，有供应商的总销售额公式如下：

结合式（4）和式（5），可以很容易得到供应商的总利润公式是：

在式（6）中，可以看出，这是一个求解最优订货量的问题。因此，将它转化成公式（7）：

1.3 模型的求解

式（7）是一个整数规划问题，于是首先将式（7）转化成下面的标准形式：

对于式（8）的整数规划，解决的方法有很多，其中对于变量数目比较小的可以用穷举法来得到优化解，但本文将采用割平面法来解决式（8）中的问题。有以下算法步骤：

Step1：首先不考虑变量xi≥0的约束取整，而是通过单纯形法解决相应的线性规划问题。当这个问题没有可行解或者最优解是整数的话则停止，否则转到Step2。

Step2：在解决对应的线性规划问题的时候，首先要将式（8）进行标准化。注：算法中的“标准化”有两个含义：一是将原问题中所有的不等式约束全部转化成等式约束，这是因为采用单纯形法的要求；二是将原问题中所有非整数系数全部转换成整数，这是因为要构造“切割不等式”的要求。

Step3：再求出一个“切割不等式”，然后加到式（8）中的约束条件中去，也就是对上述线性规划问题的可行域进行“切割”，然后返回Step1。

2 案例分析

在本节中，本文将进行实例分析来验证文中的模型以及算法的有效性。首先，假设某汽车零部件供应商生产供应a、b、c三种零部件。对于该供应商来说，其预算是在一定范围内的，要求三种零部件一共不超过10 000件，但不低于5 000件，是因为既要满足一定的顾客需求，又要保证自己的最低收入。另外，a种零部件的数量最少，b种数量最多；但a种的要分别大于b和c种的一半。本文给出以下参数：

于是，得到供应商的利润函数是：

在MATLAB2016中利用上面的割平面法进行求解，得到如下结果：

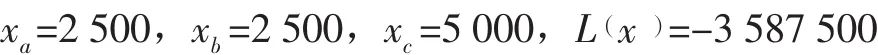
可以得出结论：在这种情况下，供应商生产a种零部件2 500件，生产b种零部件2 500件，生产c种零部件5 000件，其利润达到最大化是3 587 500元。

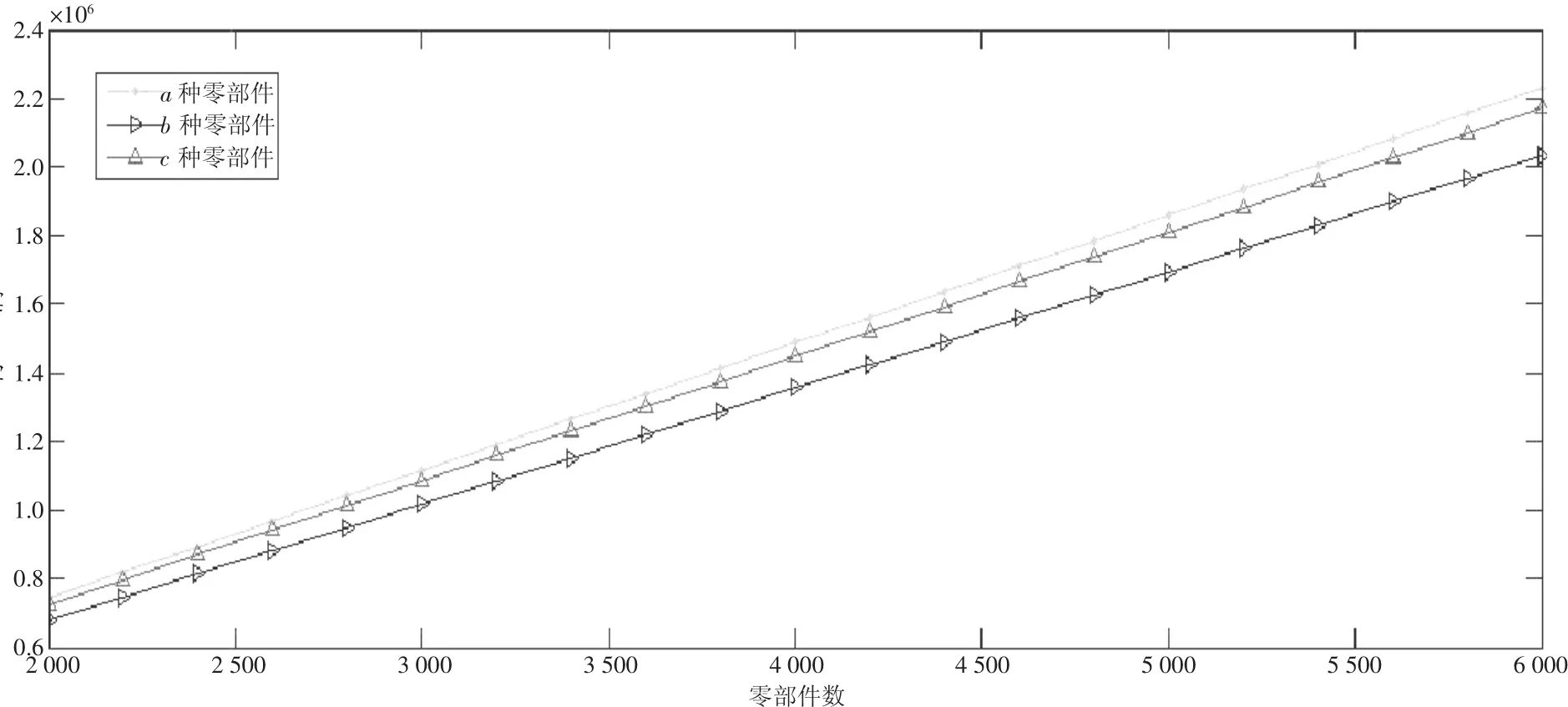
图1 供应商的零部件数量和利润关系

通过图1进一步分析，可以得到a种零部件利润大于b和c种零部件的利润。

通过上面的案例分析与求解，可以验证本文提出的模型是正确的，求解的算法也是可行且有效的。

3 总结

本文在经济全球化的背景下，考虑多运输渠道的供应商生产供应多种零部件的最优订货量，研究发现该供应商可以作出最优的决策，并且获得最大的利润。首先，本文通过构建一个整数规划的优化问题，并且利用割平面算法求解最优的目标函数。然后，证明了算法的有效性和可行性。最后，通过分析现实中的实际案例，得到供应商的最优决策使其利润最大化。本文的贡献在于：首先，将现实中的供应链问题通过数学建模的方法使其具体化，并且提出一个有效的算法使问题得到充分解决；其次，本文的方法可以为现实中的供应商提供方法论的支持以及实际的技术指导。最后，提供了丰富的管理见解。

但本文还有许多方面有待完善：（1）供应商的运输方式可以作为决策变量；（2）顾客的取货方式也可以作为决策变量；（3）本文并没有考虑空中运输方式，在将来的研究中，空运可以考虑到本文提出的模型当中。