含批处理和多订单任务的配送中心调度问题

冉文学，李子悦，焦香萍 RAN Wenxue,LI Ziyue,JIAO Xiangping

（云南财经大学 物流学院，云南 昆明 650221）

随着商业的飞速发展，尤其是在电子商务环境下，订单具有小批量、高频次等特征，所以有必要对配送中心的订单作业过程进行优化，提高拣选效率。而订单分拣是配送中心作业的重要环节之一，传统的仓储操作中，订单分拣是最耗费时间和劳力的一项工作，成本约占总仓储费用的55%[1]。作为物流配送中心的重要组成部分，订单分拣是整个订单处理中最重要的环节，对整个物流配送中心的效率产生直接的影响。所以，如何对配送中心分拣系统进行优化一直是第三方物流企业非常关注的问题。

1 国内外文献综述

1.1 订单分批处理

国内外学者对订单拣选效率优化方法的研究主要集中在拣选路径、订单分批和分区拣选等方面，但Peterson[2]认为订单分批策略更有利于拣选效率的提升。1990年Ackerman[3]首次提出了订单分批的概念，之后陆续出现了相关研究。Bukchin[4]从最小化订单延迟时间的角度决定订单分批的开始时间。AH Azadnia[5]等人为了最小化订单延迟提出了一种基于加权关联算法和遗传算法的混合算法来优化订单的分批策略。孙洪华等（2014）[6]对订单分批前后分别按照传统穿越策略、S型策略和GA优化策略3种不同路径方法进行分析，算例分析证明，采用订单分批与GA路径优化的策略组合，其拣货路径距离最短，节约量最大，效率可以提高40.33%。李晓杰（2016）[7]针对移动货架仓库系统中的货位分配和订单分批问题，分别设计了其相似度函数，并建立了聚类模型，提出了一种移动式货架系统的策略评估模型，最后比较6种策略组合的效果，得出了具有现实指导意义的结论。胡小建等（2017）[8]提出了改进的Canopy-k-means算法，采用Canopy算法依据最大最小原则生成初始聚类中心，并使用k-means聚类算法对其进行优化获取分批结果，针对不同规模的订单数据集，比较了该算法和先来先服务、k-means以及Canopy-k-means算法的实际效果，结果表明：该算法可以避免k-means算法中k值选取的盲目性，同时可以有效地提高分拣效率以及降低分拣批次。

1.2 订单分拣

基于自动化分拣系统（如图1）的自动化分拣设备通过恰当的分拣作业，最后可以节省相当大的人工成本，而在传统的物流配送行业里，平均订单分拣一项就占运营成本的62.5%。

图1 订单分拣系统

Chen等[9]利用分拣系统流程多个订单属性之间的关联提出一种数据挖掘方法，它基于整数规划的聚类算法将订单相关性作为目标变量0或1进行拟合，得到的模型经证明对解决问题具有一定的正向效应。邵刘霞等（2012）[10]考虑采取ABC存储策略运用在客户随机到达的订单中，将一些基础的遗传算法用在物品品类和数目随机时的双区型仓库布局拣选路径的优化，并以人工订单系统为对象，建立了人工订单拣选系统的优化路径模型。冉文学等（2013）[11]为了提高分拣系统的效率将间歇停机考虑到自动化分拣线之间，研究出了一种新的物流设备一单元物料分拣订单缓存器，实践证明该研究可以将自动分拣线的间歇停机率优化了百分之二十，有效提高分拣线的分拣能力。李建明、雷斌等（2017）[12]在串行顺序拣选策略的基础之上提出了混合拣选策略，并建立了对应的时间模型，较大程度压缩了订单之间的间距，提高了分拣系统的拣选效率。

本文在现有研究的基础上运用0-1混合整数规划模型对3阶物流中心调度问题建模，并且利用协同优化算法在不改变物流中心原本的硬件设备的基础上对第2阶段的一个子空间进行优化，从而达到提高物流中心作业效率的目的。

2 基于含批处理和多订单任务的物流中心调度建模

2.1 问题描述

配送中心操作系统中存在有2种流向（到货卸车流和装车配送流）的订单，其中任意一种流向的订单都要历经从到货卸车到配送中心再到装车配送3个阶段，流向相同的订单经历的阶段也相同；而对于任意一种流向的订单，各个阶段都有若干个无相关性的并行机可以供它选择。在前沿作业环节，并行机属于批处理机制，对应容纳多台输送设备可以同时到货卸车，即到货卸车点。对于任意一种流向的订单，每个阶段都没有缓冲区；对于任一种流向订单的第2阶段，即订单在配送中心的分拣作业，有上游和下游设备以及订单顺序有关的准备和处理时间。综上所述，本文将不同流向的订单流归纳为2种订单，即到货订单和配送订单，并对含有批处理机制和多订单任务特征的物流中心调度问题进行了简洁的描述，如图2：

在图2中，含批处理机制和多订单任务的物流中心调度问题具有下列特点：

（1）对于不同的订单任务，阶段1和阶段3都有不同的专用机集合，它们分别为到货订单和配送订单服务；

（2）对于配送中心的任何订单，都历经了3个阶段，且每一个阶段都有若干台不相关的并行机供该种订单选择；

（3）相邻两个工序之间没有缓冲区；

（4）阶段1和阶段3中，设备集合之间存在一部分的重合，这会使现有资源的竞争加剧；

（5） 在阶段2中，任意订单i的作业时间Hi2无法预知，但它与n（Oi1）和n（Oi3）之间的间隔路程成正比。n（Oi1）和n（Oi3）是订单i在阶段1和阶段3的操作，因此Hi2与设备和顺序呈正相关；

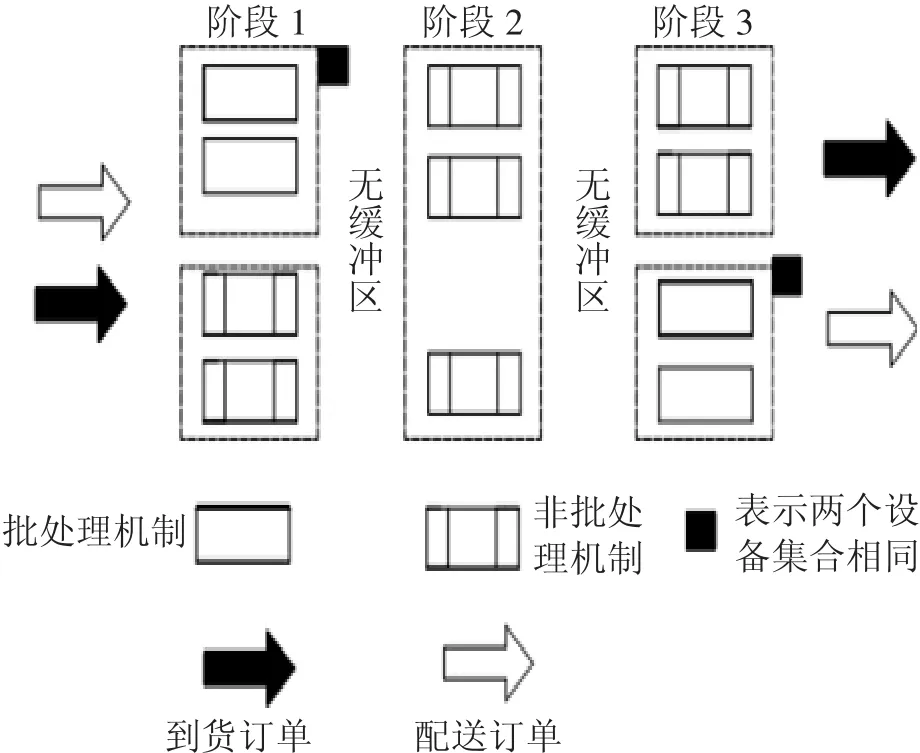
图2 带有批处理机制和多订单任务的3阶物流中心调度问题

（6） 阶段2中，任意订单i的准备时间pi2无法预知。若Oj2仅在Oi2之前，Oj2与Oi2间的计划时间pj2i2也可用pi2表示，简写为pji2。那么pji2与n（Oj3）与n（Oi1）间的间距正相关，所以pi2和设备及顺序有关；

（7）存在并行机，一次可以处理多个订单。例如到货卸车点的货车，可以同时装卸多个订单。但是只有当阶段2的设备与之协同配合，当前设备才能释放。

2.2 数学模型

针对配送中心的调度问题，充分考虑到批处理、多订单任务和无缓冲等特征，建立了0-1混合整数规划模型，具体如下：

（1） 基础符号

订单索引i,j∈N=N-∪N+,i≠j,N-和N+分别为到货订单和配送订单集；拣选流程索引L=1,2,3；S阶段的设备索引mS∈MS，MS是S阶段的设备集，是到货订单和配送订单的设备集，存在分别表示物流中心的大门、混合分拣线、集货卸车点和发货装车点的集合；分别表示非批处理机制和批处理机制的排序集合：表示订单i在s阶段的作业；分别表示属于到货订单任务中的订单i处于阶段1和阶段3的操作时间；表示属于配送订单任务中订单i在阶段1和阶段3的作业时间；tab表示订单从设备a到设备b的操作时间（已知）；H表示一个大数。

（2） 决策变量

若Ois在设备m进行操作，那么Xism=1，反之Xism=0；若Ois和Ojs在同一设备m上操作，那么Yijsm=1，反之Yijsm=0；若Ois是Ojs在m上的前一操作，则Zijsm=1，反之Zijsm=0；若Oi1和Oi3分别由m1和m3处理，那么Uim1m3=1，反之Uim1m3=0；若Oj2是Oi2的紧后操作，在m2处理，并且Oi3和Oj1分别由m1和m3处理，Vm2im3sm3=1，反之Vm2im3sm3=0；若OiS在PS处的顺序索引为b，则，βiSb=1，反之βiSb=0；若OiS在PS的顺序索引与Ojs一样，则λijsb=1，否则λijsb=0；Pis为Ois的作业时间；Ris是Ois和Ojs之间的计划时间（Ojs为Ois的紧后操作）；Tis表示Ois最初的处理时间。

假如只考虑阶段2设备的准备时间，将其他阶段设备的准备时间包括在操作时间里，混合整数规划模型如下：

其中，目标函数（1）获得最短的完成总时间；

公式 （2） 和公式 （3） 定义了3个元素（i,s,）m，担保到货订单和配送订单集合中的任意订单的任何作业仅仅只能由一台设备进行操作，并且强制定义了各项工序可以处理不同订单任务中订单的设备种类；公式（4） 定义了第1（3） 阶段并行机的批处理能力（等于2）；

公式（5） 到公式（9） 定义了3个元素（i,k,b），确保任意Ois只占用Pk中的一个位置，同批订单占用位置相同；

公式（10） 依据xism和xjsm来定义yjsm；

公式（11） 依据订单是否同批定义λijsb；

公式（12）保证处于同一批的订单绝对同机处理；

公式（13）保证处于同一批的订单会被分配到相同的设备上，根据有关文献，此非线性约束确定了4个元素（i,s,m,）b；

公式（14） 定义了当Ois为Ojs的前一作业时，zijsm=1；

公式（15） 表明只有当xi1m1和xi3m3的值都为1时，uim1m3的值才为1，反之为0；

公式（16）定义了和设备与顺序有关的处理时间；

公式（17） 定义了当xi3m3,xj1m1和zij2m2的值都为1时，那么vm2im3km1=1，其他等于0；

公式（18）定义与设备及顺序有关的计划时间；

公式（19）保障所有订单开始处理的时间都大于0；

公式（20）确保任意订单在每个操作时间的顺序；

公式（21）表示订单要开始被处理时，它的时间必须满足事先定义的顺序限制；

公式（22）确保同批订单在任意阶段是同时开始处理的；

公式（23） 和公式（24） 表示只有订单i的下一个操作Oi（s+1）开始，m才能被运行，且只有m做好准备，后一操作Ojs才能开始。

3 模型求解以及案例分析

含批处理机和多订单任务特征的3阶配送中心调度问题属于大规模的组合优化问题，在多项式时间内不可能精准地解决此问题，所以必须对该3阶配送中心的调度问题的每个子空间的每个子系统进行设计优化。本文设计了一种协同优化算法来解决基于阶段2的物料搬运车状态变化，如图3。其得到的解的质量通过下面的仿真案例进行评估。

图3中含批处理和多订单任务的3阶配送中心的调度问题的第2阶段的设备—物料搬运车如果处于空车状态，那么它将申请和获取工作，此过程只发生在集货卸车点X-或月台Y，即处于空车状态的搬运车在X-时，获得到货订单工作（用工作1标记路线和任务种类）或配送订单工作（用工作2标记路线和工作种类）；处于空车状态的搬运车在Y时，获取配送订单工作（用工作3标记路线和任务种类）或到货订单工作（用工作4标记路线和任务种类）。当空的搬运车在获取任务时，此搬运车明确了工作路线，并且按顺序访问路线上的设备。月台、发货装车点、集货卸车点的设备对应的是物料搬运车，设备对物料托盘仓库群装盘或卸盘，从而改变搬运车的状态为实车或者空车。为了尽可能地让搬运车不空跑，集货卸车点发出的工作申请优先考虑“工作1”，同理可得月台发出的工作申请优先考虑“工作3”。对任意搬运车而言，最佳组合应为“工作1”~“工作3”或“工作3”~“工作1”，这样能减少搬运车空车及空跑次数。

综上所述，基于设备状态变化的协同算法如算法1和算法2所示。涉及的符号如下：

D=D-∪D+是到货和配送订单工作的并集。

S是处于空车状态的设备（物料搬运车）集。

L（i）=（l1,l2）是设备i∈M2实行下个工作的路线，l1和l2为装和卸i的设备。

针对m∈M1∪M3，φ（m）是和m搭配的在途和排队的空搬运车之和；ω（m）为m装卸订单的数量；Q（m）⊂C是m∈Mm的任务排序集合，根据装卸盘的顺序要求，事先已知。

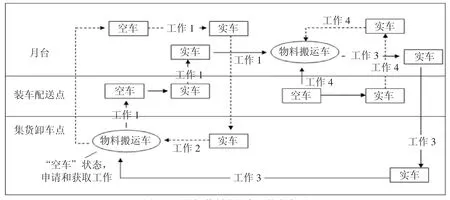
图3 “设备/物料搬运车”状态变迁

Y和X-为月台和集货卸车点的地点集。

其他符号请参照本文前面的基本符号说明。

3.1 算法1 基于“设备/物料搬运车”状态变化的协同算法

（1） 已知任务集D≠φ，令S=φ，判定阶段2中的设备状态，若i∈M2空车，则S=S∪｛｝i。

（2） 若S≠φ，获取首元素i及其方位P（i）；反之转（3）。

调用算法2，获取i相应的工作j和路线

若S=φ，则转（2），反之转（3）。

（3）基于时间调度法运行仿真程序。

①i∈M2，更新i的状态和地点P（i）；若i是空车，那么

②∀m∈M1∪M3更新φ（m）。

③若S=φ，那么转向（2）。

④若D=φ，那么转向（3）， 反之转向（4）。

（4）得出仿真数据，利用下界理论对解进行评估。

算法1中牵涉到算法2，它根据设备的平均操作进行任务分配，以并行机的效率优先，即先满足并行机的要求，以防并行机出现长时间等待。

3.2 算法2任务分配子程序

（1） 根据P（i），明确i请求的工作类别 τ（i）。

P（i）∈X-且D+≠φ，τ（i）=工作1；P（i）∈X-、D+≠φ，D≠φ，τ（i）=工作2；P（i）∈Y且D-≠φ，τ（i）=工作3；P（i）∈Y、

（2） 基于 τ（i）确定L（i）=（l1,l2）上的设备种类。

若τ（i）=工作1或工作4，那么若 τ（i）=工作2或工作3，有且

（3） 重复以下①～④，直至确定l1和l2。

①使l为现在需确定的设备，根据l的所属关系定义设备集M1。

②在Ml中，∀m∈Ml，依据φ（m）的值对设备排序；根据ω（m）非减，对φ（m）相同的设备排序。

③若M1⊆GQ，把φ（m）值为偶数的设备排在φ（m）值为奇数的设备之后。

④得到M1的第一个元素k，使l=k，φ（k）（ω（k））=S*D。

（4） 基于设备l1确定任务k。

3.3 案例分析

本文利用与文献[1]（Chen L et al,2010）一样的下界理论对配送中心的调度问题进行评估。仿真案例与设备的运行参数选用文献[1]的数据进行设置，如表1。

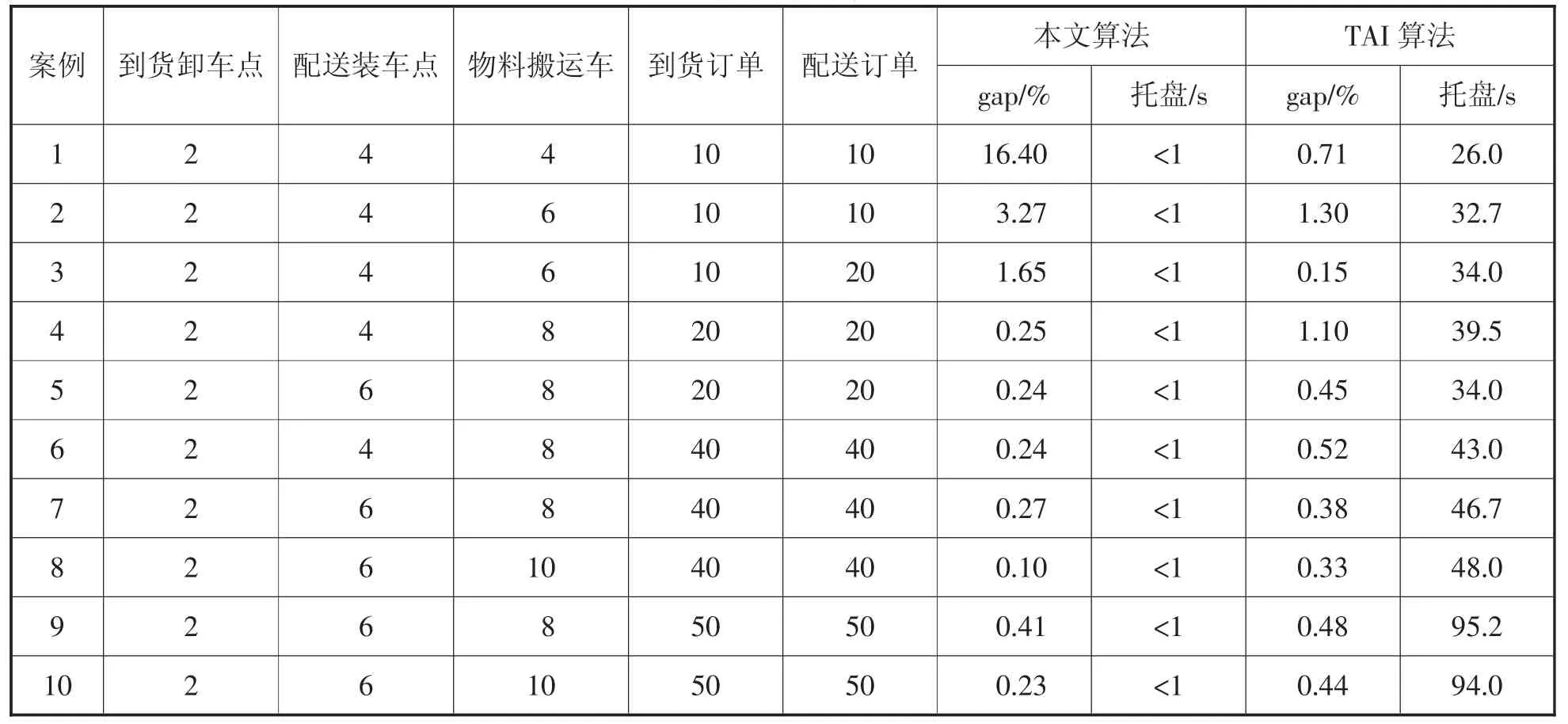
表1 案例及其仿真结果

为了确定“对于任意物料搬运车，最佳工作搭配应是①～③或③～①”的假想，本文分别对边装边卸和先卸后装进行仿真，结果如图5所示。边装边卸的Makespan值显然更小，原因是它运用“①～③”或“③～①”的组合减少了搬运车的空车状态，缩短了空跑时间，从而使搬运车的等待时间得到优化。此仿真证实了上述设想，保证本文算法的合理。

为了评估本文的算法1，使表1中的10个仿真案例都运行100次。算法性能评估采用下界理论，仿真结果如表1所示，算法间隙结果比较如图4。协同算法与TA1算法相比，其gap在案例1至案例3中较好，但每秒托盘数在所有案例中全小于1s；TAl算法每秒托盘数含有非延迟多重插入特征，其每秒托盘数在例1中最短（26s），在例10最长（94s）。

在图5中，而协同算法与TA1相比，其gap在例1至例3中相比较，结果较差，其他都优于TA1算法。原因如下：①例1至例3的工作量相对较少，仿真正在准备阶段；②协同算法的核心是操作平衡，它要求一定的设备和工作来反映其性能优势。因此，在案例问题中，协同算法可以实现比TAl算法更好的间隙性能。

4 结束语

随着社会的不断网络化，物流信息化和自动化建设越来越受到重视，分拣作为物流配送的关键环节，在整个物流系统中不可或缺，研制符合我国订单分拣特点又经济实用的自动化分拣系统是物流研究人员面临的一个重要课题。本文在进一步深入分析国内外订单分拣现状的基础上，利用0-1混合整数规划模型对含批处理和多订单任务的配送中心调度问题进行建模分析，提出了面向多订单分拣的自动化分拣作业系统模型，并在该模型基础上运用协同优化算法在一定程度上订单的自动分拣效率得到了提高。

图4 算法比较

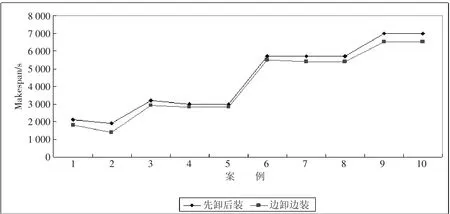
图5 不同方式下的Makespan比较

如果自动分拣系统能够符合订单分拣的特点，就可以大幅地提高订单分拣的效率，同时降低工人的劳动强度。该领域还存在许多问题需要更进一步的完善和研究，例如，分拣系统的建模仍然需要调整，协同算法需要更深入的优化等，这些都需要以后进行不断深入的研究。