两种低转速特性外推方法的对比

2019-04-09郭佳男

工程与试验 2019年1期

周超，郭佳男

(中国飞行试验研究院，陕西西安 710089)

1 引言

获取涡轮发动机低转速部件特性，是使用基于部件模型模拟航空发动机启动过程的前提。但是，目前已知的特性几乎都是慢车以上获得的，一方面试验花费大、周期长，另一方面，试验过程必须考虑二次流损失、雷诺数、流量的连续性等因素的影响，很难获得发动机各部件的低转速部件特性。即使通过试验方法获得的结果，也必须进行修正[1]。因此，预测和建立低转速部件特性图显得尤为重要。

发动机低转速部件特性预测方法有很多，常用的有特性外推法、逐级叠加法和逐级分解法[2]、神经网络法[3]、遗传算法[4]、支持向量机[5]、基于流动相似原理指数法[6]以及基于抛物线法[7]。

特性外推法是基于发动机大量的试验数据以及经验关系来估算不同外界条件下发动机各个部件的流量、热焓、效率等参数，这种方法比较简单，但是准确度不高，需要依靠大量的试验数据以及经验公式。逐级叠加法和逐级分解法使用多项式的方法来模拟压气机的特性，再外推这些多项式来得到压气机的低转速部件特性。但分析认为，该方法从中等流量系数区到低流量系数区外推时可以得到压气机特性所需的原始数据，但极高或者极低的转速时，该方法外推出来的特性不具有准确性。逐级叠加法和逐级分解法由于需要根据部件级特性、设计点参数和部件尺寸来获得部件低转速特性，计算方法较为复杂。神经网络法在部件特性内插时具有较高的准确度，而其外推获得的部件特性则由于远离已知特性，准确性不高。

本文采用基于流动相似原理指数法和基于抛物线方法分别针对发动机压气机和涡轮特性进行外推，并将外推出的特性作为已知条件代入发动机整机模型中，进行节流计算。

2 基于流动相似原理指数法外推

基于流动相似原理指数法利用了泵类机械低转速区特性相似理论，即部件特性的参数看成与转速比成n次方关系，n的数值与所外推的部件特性参数有关。

2.1 风扇和压气机特性外推方法

根据不可压缩流的相似理论，当发动机工作在较低的工况时，风扇和压气机的参数符合以下相似定律：

流量在相似工作点上，n值取1：

(1)

功在相似工作点上，n值取2：

W1/W2=(N1/N2)2

(2)

功率在相似工作点上，n值取3：

Pwr1/Rwr2=(N1/N2)3

(3)

效率在相似工作点上相等：

η1=η2

(4)

相似工作点是按照不可压缩流中的相似原理来定义的。在已知的部件特性的最低转速下(称为参考点，下标为ref)，要预测更低转速部件特性(下标为new)的基本步骤为：

(1)根据式(1)可以计算预测转速下相似工作点的流量或者换算流量。

(2)根据式(2)，功与转速的平方成正比，可以计算得到相似点的功，然后利用式(6)计算得到相似点的压比(注：计算时认为该相似工作点下的效率相等，故可以使用参考点的效率)。

(5)

(6)

(3)利用经验公式预测转速下的相似工作点的扭矩。

(7)

式中，n取1.75，但是可以根据所预测的风扇和压气机的情况，来调整n的数值。

(4)根据风扇和压气机效率的定义，由式(7)可以得到压气机扭矩，然后根据式(8)和式(9)得到效率(式(10))。

(8)

pwr new=2πNnewTqnew

(9)

(10)

不难看出，由于所用的扭矩与转速之间的关系不是二次方，因而按照式(10)计算得到的效率就不等于参考点的效率。

根据上述步骤外推某发动机压气机特性，得到的结果如图1所示。

(a)外推前后换算流量与压比

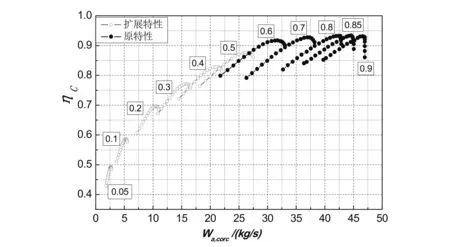
(b)外推前后换算流量与效率图1 压气机外推前后特性

2.2 涡轮特性外推方法

高低压涡轮低转速部件特性的预测方法与风扇和压气机的相似。

功在相似工作点上，n值取2：

W1/W2=(N1/N2)2

(11)

换算流量在相似工作点上与转速成m次方的关系：

(12)

换算扭矩在工作点上与转速成n次方的关系：

(13)

式中，m和n分别称为流量和扭矩的指数，需要根据特性图最低和次最低转速下涡轮特性的扭矩(或流量)的变化关系来确定。m和n的数值确定之后，接下来外推步骤与压气机外推相似。外推某发动机涡轮特性得到的结果如图2所示。

(a)换算流量与涡轮落压比关系

(b)效率与涡轮落压比关系图2 相似理论外推的涡轮特性

3 基于抛物线法外推

基于抛物线法外推，首先将压气机和涡轮特性的表征方法进行转换，然后利用在零转速特性的特点以及最低两条转速线上的点进行低转速特性外推。

3.1 风扇压气机特性外推方法

为了方便风扇/压气机在低转速特性计算以及外推，首先将风扇/压气机特性图表征方法进行转换，使用Tqcor扭矩代替效率ηc；利用风扇/压气机出口换算流量W2acor替换传统的进口换算流量Wacor。转换后特性的表达方式为：

(14)

其中，Tqcor和W2acor计算公式为：

(15)

(16)

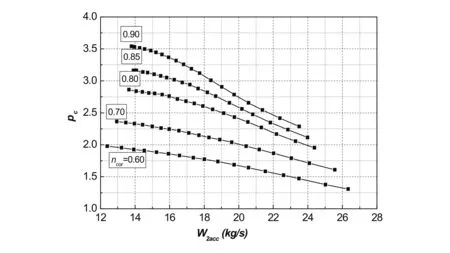
(a)压气机压比与出口换算流量关系

(b)压气机压比与换算扭矩关系图3 压气机转换后特性图

图3为某压气机表征方式转换后的效果图，风扇/压气机在等低换算转速下，压比与出口换算流量近乎成线性关系，而且随着转速的降低，斜率越小，越来越平缓，所以在零转速工况下风扇/压气机特性应该是压比πc=1.0的水平直线。此外，风扇/压气机在等低换算转速下，扭矩与出口换算流量关系为近乎斜率为负值的直线，而且不同换算转速间互相平行，而且在零转速工况下必经过Tqcor=0.0、W2acc=0.0点。在外推特性之前，应该定义3个参数：流量系数φ、温度系数ψ以及压力系数ψs。

(17)

(18)

ψs=ψ×ηc

(19)

在发动机实际应用中，φ、ψ和ψs这3个参数分别代表了风扇/压气机特性中的流量、效率和压比。当压气机/风扇工作在低转速情况时，内部气流的马赫数比较小，如果换算流量不大，则可以认为气体是不可压缩流。此时流量系数φ、温度系数ψ以及压力系数ψs对描述压气机/风扇的特性具有重要意义。在低转速不可压缩流的假设下，相似点的效率相等，因此在低转速区域最高效率值与换算转速几乎无关，在零转速下效率峰值(等换算转速线上效率最高点的连线)的切线斜率为零。

如果不考虑导叶角度可调的影响，风扇/压气机特性从高转速过渡到低转速一定是平滑的，因此作出假设，φ=f(ncor)图中，对于同一个压力系数ψs，从中间转速过渡到低转速的变化曲线为抛物线，并且这条抛物线满足以下条件：已知最低和次低两条等转速线上的相似点(即不同换算转速线上压力系数相等的点)应该在抛物线上；抛物线在零转速处的斜率为零。根据以上假设外推某型压气机特性图，结果如图4所示。

(a)外推前后出口换算流量与压比

(b)外推前后出口换算流量与扭矩

(c)外推前后换算流量与压比

(d)外推前后换算流量与效率图4 外推结果

3.2 涡轮特性外推方法

同压气机特性一样，涡轮特性的表达方式也需要转换，用换算扭矩替代涡轮的效率，该描述方法是：

(20)

转换后特性如图5所示，涡轮换算流量与换算转速之间关系接近线性，而且落压比越小，斜率越大，而且在落压比为1.0时要经过原点；涡轮换算流量与换算转速之间在不同的落压比之间接近直线而且互相平行，而且在压比为1.0时经过原点。

(a)涡轮换算流量与换算转速关系

(b)涡轮换算扭矩与换算转速关系图5 涡轮转换后特性图

涡轮外推过程与风扇/压气机外推方法几乎一样，流量系数φ、温度系数ψ以及压力系数ψs这3个参数的定义与风扇/压气机参数一样；换算扭矩依然按照同压力系数情况下抛线法进行外推，而且扭矩各抛物线必须要斜率为零；不同的是不再是按照流量系数的抛物线，而是按照流量系数的倒数1/φ=f(CNHP)进行抛物线外推，并且在零转速上斜率为零。外推得到的结果如图6所示。

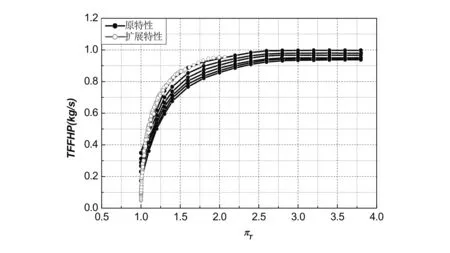
(a)换算流量与涡轮落压比关系

(b)效率与涡轮落压比关系图6 基于抛物线法外推得到涡轮特性

4 两种外推特性法稳态节流特性对比

现将两种方法外推的压气机和涡轮特性作为已知条件，代入发动机整机模型中。本文利用部件级模型建立发动机整机模型[8]，进行节流计算，对比结果如图7所示。

(a)两种外推方法压气机效率

(b)两种外推方法涡轮效率

(c)两种外推方法压气机喘振裕度

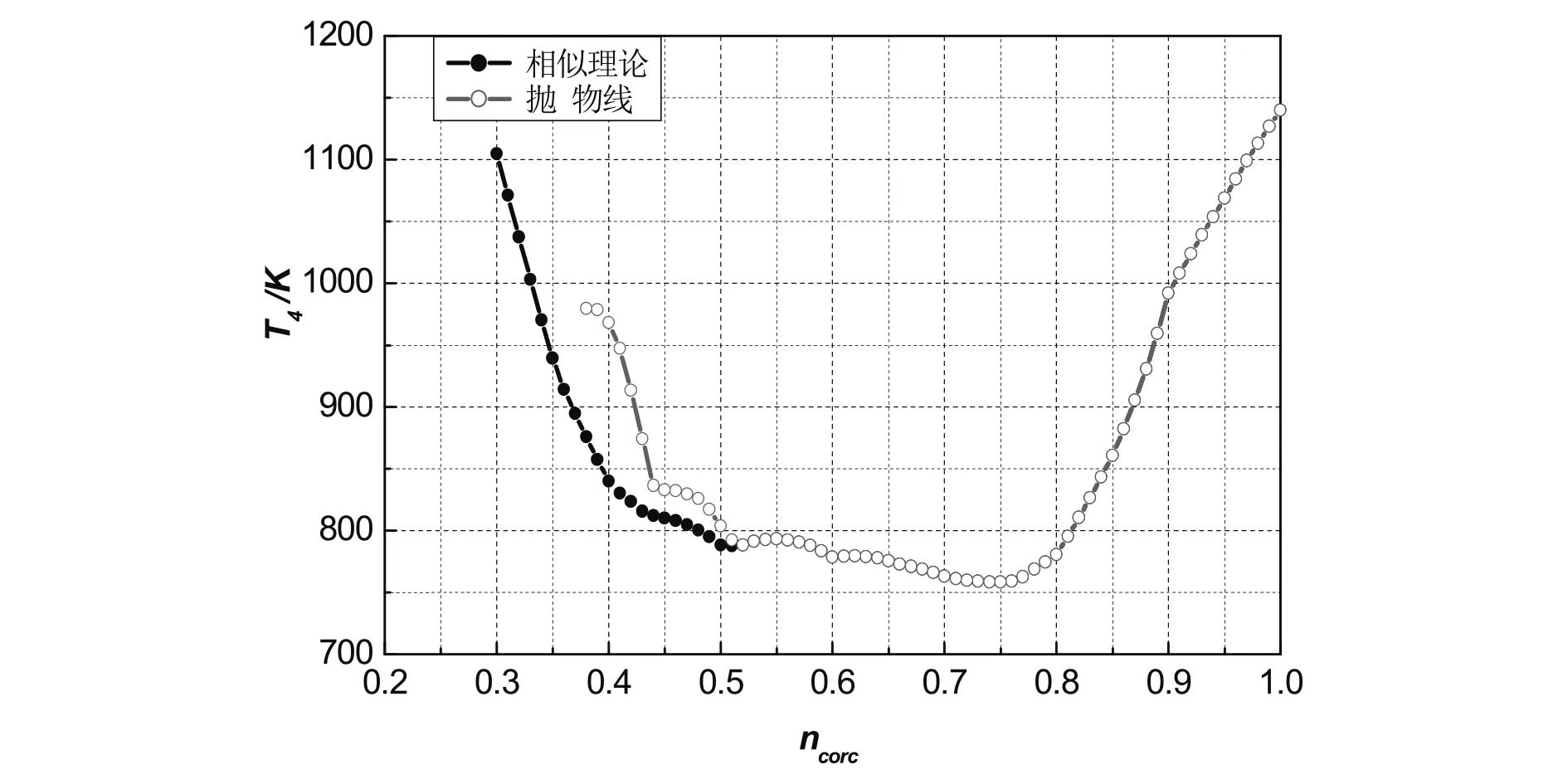
(d)两种外推方法涡轮前总温图7 两种外推特性节流参数对比

由图7(a)和图7(b)可得，在低转速下，基于抛物线法外推特性的压气机、涡轮工作效率较低，所以其涡轮前总温、油气比较高；采用相似原理指数法外推的特性，发动机转速可以节流到30%，而基于抛物线法外推的特性可以节流到37%。由图7(d)可以看出，基于相似原理指数法不能往下节流的原因是涡轮前总温超界，但是抛物线法外推的特性在最低节流点压气机喘振裕度、涡轮前总温、燃烧室油气比均在安全工作范围之内，造成其不能继续节流的原因以及在低转速下进口流量减小的原因需要基于涡轮工作线来分析，如图8所示。