对某些强度及刚度问题计算的讨论

2019-04-09刘奇元

工程与试验 2019年1期

吴晓，刘奇元

(湖南文理学院机械工程学院，湖南常德 415000)

1 引言

众所周知，材料力学的任务就是在满足强度、刚度及稳定性的要求下，为设计既经济又安全的构件，提供必要的理论基础和计算方法。在工程问题中，一般构件都应有足够的强度、刚度及稳定性，但对具体的构件，又往往有所侧重。例如，储气罐主要是要保证强度，车床主轴主要是要具备一定的刚度，土木建筑工程中的深梁弯曲变形挠度要考虑剪切变形的影响，工字钢、T形钢的弯曲应力有时要考虑剪力的作用。

以上工程实际中的强度和刚度问题，材料力学已建立了计算方法。一般情况下，这些计算方法的计算精度是可靠的。但在一些特殊的情况下，材料力学建立的强度和刚度问题计算方法，还存在某些不足。另外，在教学中，学生对强度理论的适用范围还不是很明确。针对以上材料力学教学中存在的问题，笔者在此抛砖引玉，对材料力学中某些强度及刚度问题计算方法的应用范围进行了简单讨论。

2 销钉连接叠层梁的弯曲计算

文献[1]是天津大学主编的《工程力学实验》教材，开设了图1所示叠层梁的弯曲应力试验，以此来测量应力分布，但没有给出弯曲应力及销钉剪力计算公式。当时，由材料力学可知，销钉连接叠层梁截面平衡条件为：

N1=-N2=N

(1)

M1(x)+M2(x)+Nh=P(l-x)

(2)

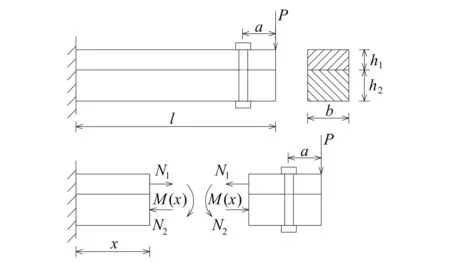
图1 销钉连接时的叠层梁

由于销钉连接叠层梁接触面的纵向变形相等，则：

(3)

把式(2)在梁长(l-a)上积分，可把式(2)、式(3)分别化为：

(4)

(5)

叠层梁的各层梁弯曲时有下式成立：

(6)

式中，ρ为叠层梁上层梁的弯曲曲率半径。

把式(6)在梁长(l-a)上积分，可得：

(7)

由式(4)、式(5)可以求得：

(8)

把式(2)化为下式：

M(x)=M1(x)+M2(x)=P(l-x)-Nh

(9)

利用式(6)、式(9)可以求得：

(10)

(11)

由式(10)、式(11)可以看出，叠层梁截面弯矩与叠层梁的各层梁截面弯矩在本质上是非线性关系。所以，图1所示销钉连接叠层梁任意截面上下层梁的弯曲应力最大值为：

(12)

由强度校核条件可知：

σ1≤[σ]，σ2≤[σ]

(13)

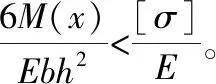
(14)

所以，文献[2]认为，叠层梁弯曲时，上下层梁的曲率半径近似相等，即：

(15)

3 四个强度理论计算的适用范围

在三向拉伸应力状态下，即使像低碳钢这样的塑性材料，都会发生脆性破坏。可以知道，不论是脆性或塑性材料，在三向拉伸应力状态下，都会发生脆性断裂，并宜于采用最大拉应力理论。

对于脆性材料，在二向或三向应力状态下，应采用最大拉应力理论。在二向或三向应力状态下，最大和最小主应力分别为拉应力和压应力的情况下，则可采用莫尔强度理论。

对于像低碳钢这一类的塑性材料，在三向拉伸应力状态以外的各种复杂应力状态下，材料都会发生屈服现象。所以，塑性材料一般采用形状改变比能理论。但在有些计算中，也采用最大剪应力理论。这是因为，最大剪应力理论的物理概念较为直观，而且按此理论所得计算结果也是偏于安全一面的。在土木工程中，应用形状改变比能理论比较多，例如对钢梁的计算时，一般均采用形状改变比能理论。在机械工程中，应用最大剪应力理论较多，如承受内压作用的钢管进行计算时多采用最大剪应力理论。

在三向压缩应力状态下，不论是塑性材料还是脆性材料，通常都发生屈服破坏，故一般应采用形状改变比能理论。

下面可估算一下形状改变比能理论与最大拉应力理论的计算误差。

形状改变比能理论、最大拉应力理论的相当应力表达式分别为：