白车身固有振动特性CAE及试验分析对比

刁杰胜，刘文慧，尹杨平



白车身固有振动特性CAE及试验分析对比

*刁杰胜，刘文慧，尹杨平

（奇瑞商用车（安徽）有限公司工程研究院，安徽，芜湖 241000）

汽车NVH性能设计需对白车身的固有振动特性进行分析。本文根据白车身模态实验的状态，建立相应的有限元模型，并对CAE和试验结果进行对比。结果表明：白车身的前三阶振型一致，第四阶振型基本一致；各个振型对应的固有频率误差在5%内；前二阶试验和CAE的固有频率略低于目标值要求，暂时风险接受，待路试试验验证后再决定是否进行优化；第三阶和第四阶试验和CAE固有频率都满足目标值要求。根据CAE规范分析得到的结果具有较高精度，针对本车，可用CAE方法进行模态优化，这对降低汽车生产成本，改善NVH性能具有重要意义。

固有振动特性；NVH性能；试验分析；CAE分析；汽车生产成本

汽车生产厂家在设计整车性能时都非常重视NVH性能，NVH性能包括振动、噪声、舒适性等[1]。而振动是噪声产生的重要原因，也会直接影响乘客的乘车舒适性。当激振频率接近或等于固有频率时，车体会产生共振，在设计过程中需保证白车身各阶固有频率不能低于目标值。白车身模态分析方法有CAE和试验两种[2-5]，白车身CAE分析和试验状态分别由汽车生产厂家的分析规范和试验规范决定，不同的分析和试验规范得到的结果不同，为验证CAE分析结果的有效性和两种分析规范的一致性，需根据试验时状态调整CAE分析的状态，并对试验和CAE分析的结果进行对比。本文通过试验分析白车身的模态，并根据试验的状态调整CAE分析模型，最终对两者的分析结果进行对比，判断两者的关联性，并验证是否满足目标值。本文为车身结构的优化提供方法，并为车身的NVH性能设计提供依据。

1 模态分析原理

白车身系统可以离散为具有i个自由度的系统，对于受迫振动的弹性系统振动微分方程为[6]：

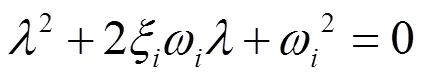
2 白车身有限元分析

本文使用Hypermesh14.0软件对白车身进行有限元建模，使用线性求解器MSC Nastran14.0进行模态分析，并在Hyper View模块进行后处理。

2.1 白车身有限元模型建立

白车身有限元模型是根据试验时白车身状态建立，包括车身骨架、副车架、前挡风玻璃、前后保险杠横梁和转向柱支架，车身骨架各钣金件用带有厚度的壳进行模拟，对壳划分网格时，单元基本尺寸为8 mm。装配各钣金件的时候，焊点采用acm单元模拟[7]，焊点大小为6 mm，粘胶采用adhesive单元模拟，焊缝和螺栓采用rigid单元模拟。各零部件为线性材料，材料属性参数如表1所示。

表1 材料属性

对白车身进行自由模态时，车身无约束，也无外界荷载。在Hypermesh荷载集中设置模态荷载，包括求解的频率搜索范围和模态的求解算法，搜索范围设为0.1-80 Hz，求解算法卡片选EIGRL。还需设置模态分析的载荷步，包括设置分析类型为模态分析，分析方法选择之前创建的模态荷载。最后设置求解输出为位移和应变能，建立的有限元模型如图1所示。

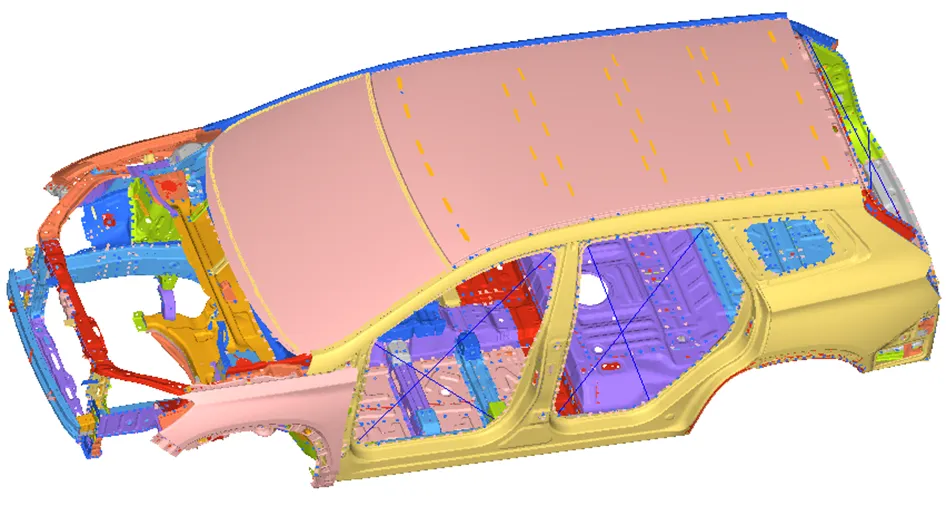
图1 白车身有限元模型

2.2 模态分析结果

低阶频率对动态特性影响较大，且汽车在正常路面上以低于150 km/h速度行驶时，路面对汽车激振频率在21 Hz以下，发动机怠速时激励频率约为27~30 Hz[8]，都为低阶频率。故从CAE分析结果中提取车身的前4阶模态振型，振型图如图2所示，对应的固有频率结果如表2所示。

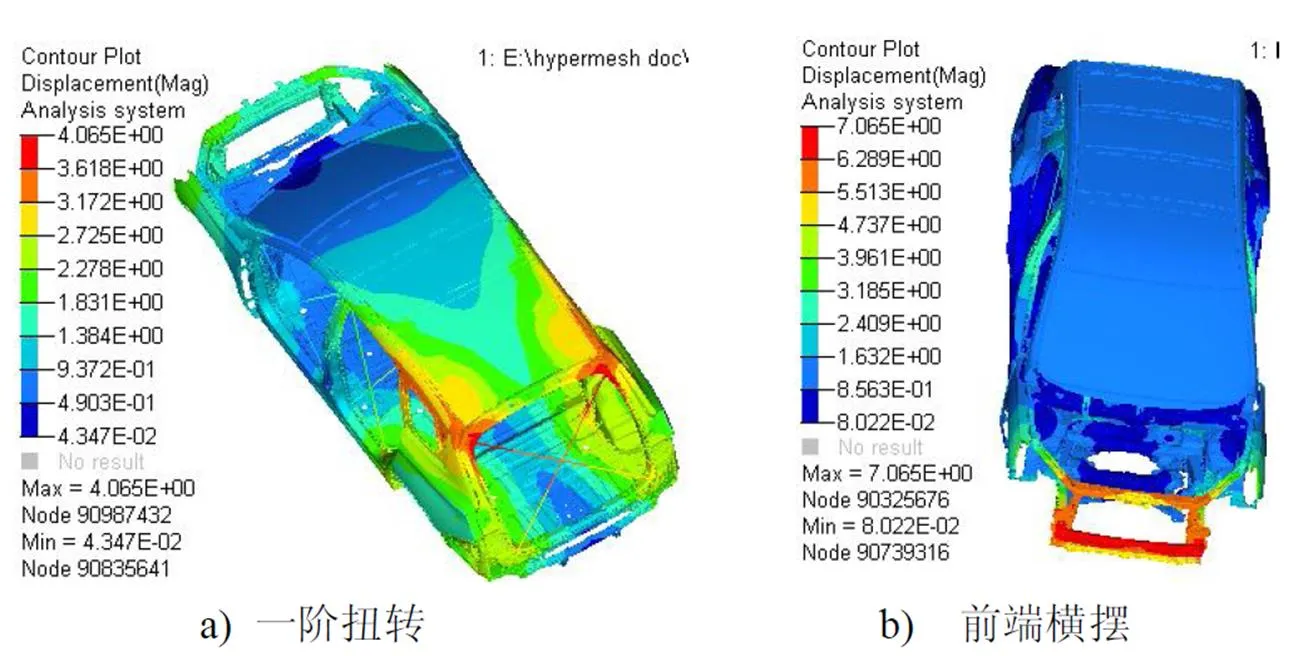
表2 CAE分析白车身各阶频率

3 白车身模态试验

试验方法是用橡皮绳对白车身进行悬挂，使白车身近似达到自由状态，再用激励器激励车身刚度较大的部位[9]，测得车身上不同位置上的加速度响应。通过计算在频域上输出的加速度响应与输入激励力的比值得到振动系统的传递函数。最后通过信号处理与模态参数识别，获得车身模态振形，模态频率与模态阻尼[10]。

3.1 测量点布置

根据白车身结构特点和试验的实际情况，在白车身上布置了将近300个测量点，每个测点都有标记和代号，测量各点相对于车身上某定点的坐标，然后在LMS Test.Lab 12 A结构动态分析软件系统上建立的白车身结构测点模型，模型由顶盖、地板、车尾、车侧身、前后翼子板和前舱测点数据组成。测点布置图和测点模型图分别如图3和图4所示。

图3 测点布置图

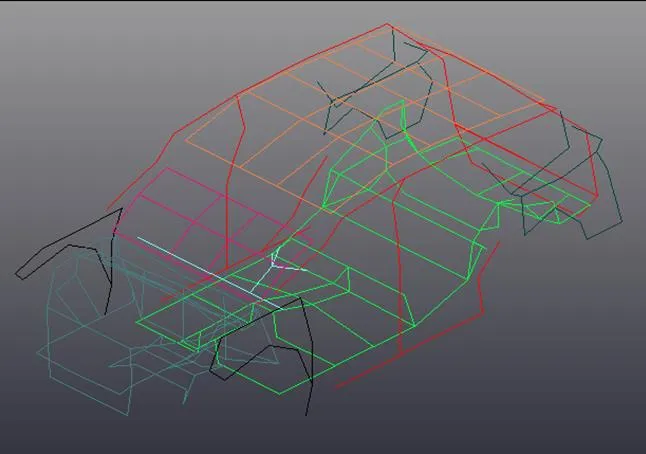
图4 测点模型图

3.2 各点传递函数测量

本试验采用MB Dynamics公司生产的MB模态激振器产生激励信号，在车身前部设置Y方向的激励，车身后部设置Z方向的激励；获取响应信号的装置采用PCB公司生产的加速度传感器；放大响应信号装置采用PCB公司生产的ICP放大器；信号调理与数据采集装置采用LMS公司生产的SCADAS III信号采集系统；模态分析计算采用LMS Test.lab 12A结构动态分析系统。各实验装置如图5所示。

图5 实验装置

获取各个测量点传递函数的流程如图6所示。

图6 测量方法流程图

3.3 模态参数识别

本试验数据用PolyMAX模态参数识别算法处理后，得到在低频率段内的模态参数，获得的稳态图如图7所示。从稳态图中可看出：各个峰都比较清晰，峰与峰之间没有耦连，各阶模态之间相互影响很小，拟合时可按单自由度模态进行处理。

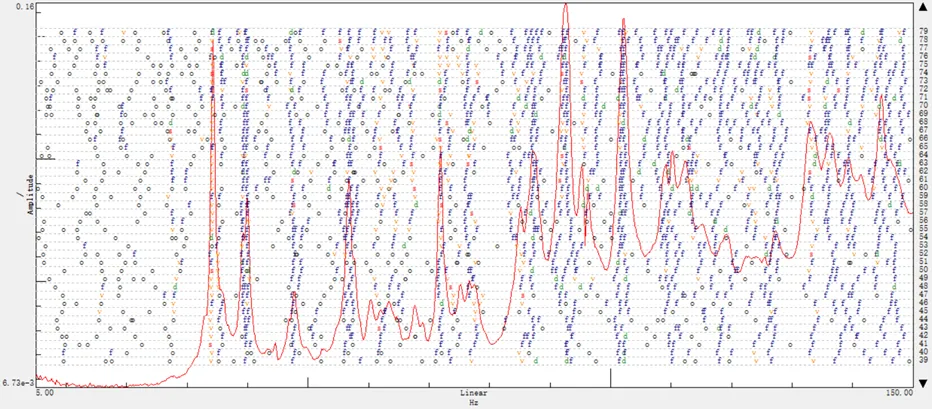
图7 用PolyMAX获得的稳态图

3.4 试验分析结果

用LMS Test.Lab 12A系统对车身所有测点的传递函数进行拟合，拟合出的前4阶模态频率见表3，车身各阶模态振型见图8。

图8 试验白车身振型

表3 试验测得白车身各阶频率

4 试验和CAE模态分析结果对比

1）振型对比：对比表2的CAE白车身振型和表3的试验白车身振型，可以看出前三阶振型一致，分别为一阶扭转、前端横摆、前端扭转，整体弯扭。试验的第四阶振型试验和CAE的挡风玻璃局部模态一致，一阶弯曲在试验结果中表现不明显。

2）固有频率对比：频率对比表如表4所示，从表中可以看出试验和CAE的各阶振型对应的频率误差分别为4.9 %、0.9 %、0.6%和1.3 %，在5 %范围内，各阶振型对应的频率基本一致，误差较小，具有较高的精度。

3）目标值对比：从表4的频率对比表可以看出，前二阶试验和CAE固有频率略低于目标值，暂时风险接受，待路试试验验证后再决定是否进行优化；第三阶和第四阶试验和CAE固有频率都满足要求。

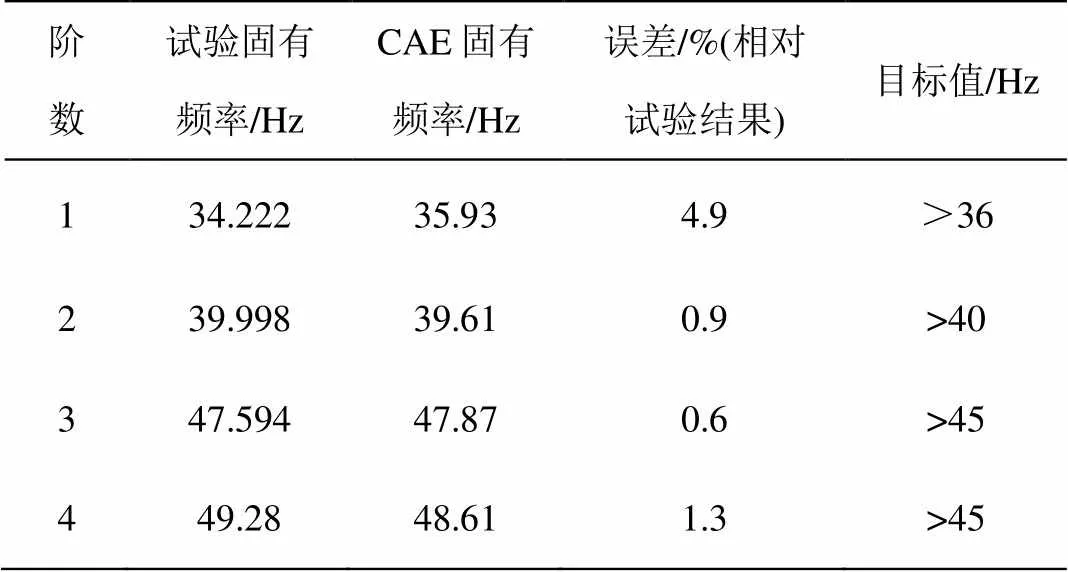
表4 频率对比表

5 结论

本文建立了白车身的有限元模型，分析得到低阶固有频率和对应振型；对白车身实车进行试验测量，得到低阶固有频率和对应振型。最后对CAE和试验的结果进行对比，结论为：前三阶振型一致，第四阶振型基本一致；振型对应的固有频率误差在5%内；前二阶试验和CAE固有频率略低于目标值，暂时风险接收，待路试试验验证后再决定是否进行优化，第三阶和第四阶试验和CAE固有频率都满足要求。根据CAE规范分析得到的结果具有较高精度，故针对本车，可用CAE方法对车身结构进行优化，这对降低汽车生产成本，同时通过避免激振频率和固有频率的重叠，对降低噪声和提高乘车舒适性等方面具有重要意义。

[1] 胡小舟,林建平,胡巧声,等. 基于模态应变能及灵敏度分析白车身模态分析[J]. 机械科学与技术, 2015, 34(9): 1415-1418.

[2] 赵常虎,郭永进,余海东. 轿车白车身骨架低阶模态特性研究[J]. 机械设计与制造, 2007,11(11):180-182.

[3] 张建,唐文献,马宝,等. 某轿车白车身试验模态分析[J]. 江苏科技大学学报, 2012, 26(2):146-149.

[4] 周长路,范子杰,陈宗渝,等. 微型客车白车身模态分析[J]. 汽车工程, 2004,26(1):78-80.

[5] Chen W H，Lu Z R. Theoretical and experimental modal analysis of the Guangzhou New TV Tower[J]. Engineering Structures,2011, 33( 12) :3628-3646.

[6] 马骊凕,朱智民,安占飞,等. 轿车白车身模态分析[J]. 振动与冲击, 2013,32(21)：214-218.

[7] 赵晶英,项顺伯,陈英俊．轻型卡车底板纵梁生产线的机器人焊接仿真[J]．机械设计, 2012,29(4):26-31．

[8] 罗明军,周帆,赵永玲. 轿车车身怠速共振分析[J]. 机械设计, 2015, 32(3):46-50.

[9] Guillaume P，Verboven P，Vanlanduit S，et al. A poly-reference implementation of the least-squares complex frequency domain estimator [C].Proceedings of IMAC 21, the International Modal Analysis Conference，Kissimmee （FL）, USA，February, 2003．

[10] 刘焕广,陈朝阳,谭继锦,等. 商务车白车身试验模态分析研究[J]. 合肥工业大学学报,2007,30(12): 1615-1619.

Contrast of CAE and experimental analysis method for natural vibration characteristic of BIW

*DIAO Jie-sheng，LIU Wen-hui，YIN Yang-ping

( Automotive Engineering Research Institute, Anhui Chery Commercial Vehicle Company, Wuhu, Anhui 241000, China)

The natural vibration characteristic of BIW (body in white) should be analyzed in the process of NVH (noise vibration and harshness) performance design for the vehicle. The finite element model is established according to the state of modal experiment for the BIW. The results show that the first three orders of mode shapes for the BIW are the same by the method of CAE (computer added engineering) and experiment. The fourth-order shape is largely consistent. Each proper frequency of each shape has a maximum error of 5%. The first two orders proper frequency measured by the two methods mentioned above are approaching the goal. Both the CAE and experiment results are accepted by risk temporarily. The optimization will be done when the results of test on road are not good. Both the third and fourth-order proper frequencies measured by the two methods meet the goal. The results have high accuracy using the method mentioned in the CAE specifications. The modal optimization for the vehicle can use the CAE method. It has significant importance to optimize automobile structures, reduce car production cost and improve NVH performance by using the CAE analysis method.

natural vibration characteristic; NVH performance; experimental analysis; CAE analysis; car production cost

U463.82

A

10.3969/j.issn.1674-8085.2019.02.013

1674-8085(2019)02-0072-05

2018-12-29；

2019-01-11

*刁杰胜(1989-)，男，安徽巢湖人，硕士，主要从事现代化设计理论、方法和CAE仿真技术研究(E-Mail: djsh0001@163.com);

刘文慧(1985-)，女，安徽芜湖人，工程师，硕士，主要从事汽车碰撞安全分析及优化技术等研究(E-Mail：lwh111052@163.com);

尹杨平(1985-)，女，安徽马鞍山人，主要从事CAE仿真技术研究(E-MAIL:yinyangping@126.com).