440nm-665nm消色差二分之一波片的二元设计

黄 艳



440nm-665nm消色差二分之一波片的二元设计

黄 艳

（漳州职业技术学院电子工程学院，福建，漳州 363000）

为了设计适用于可见光波段的消色差二分之一波片，根据复合波片理论，选用石英和氟化镁材料利用最小二乘拟合法，设计出了440 nm~665 nm范围的消色差 λ/2复合波片。理论研究和实验检测结果均表明，依据此方案设计的消色差λ/2复合波片相位延迟精度可达 λ/50，满足实际使用的需求。

应用光学；消色差；最小二乘法；复合波片；延迟精度

0 引言

光相位延迟器作为光相位调制及光波偏振态变换的重要器件，在光纤技术、光检测技术及光传感技术领域中日益广泛应用[1]。通常其制作材料都选用晶体，利用光通过晶体改变光波的振幅和相位差的特点，从而改变光波的偏振态。任何平常所说的λ/4波片和λ/2波片等都是对特定波长而言。在某种情况下，我们需要使用在一个波段范围内，其相位延迟量基本是一个常量的特殊波片，即消色差波片。消色差波片削弱了相位延迟量对波长的依赖关系，适用于较宽的光谱范围。消色差波片的优势使之大量地用于激光系统、光通讯器件以及光测试测量仪表，甚至是DVD、CD、数码相机、光学显示系统等。

消色差波片的设计方法众多[2-6]，其中双折射型消色差波片制作方法主要有两种：一种方法是可采用同种材料组合，根据工作波段选取各片厚度，及设计各片光轴之间的夹角来达到消色差功能；另一种方法是选取双折射色散相匹配、物化性能相近的不同晶体材料进行复合，两种晶体的光轴相互垂直或平行布置，由二者的双折射率相互补偿实现相位延迟量消色差特效[7]。本文采用的方案是利用石英和氟化镁组合，设计实现440 nm-665 nm可见波段内消色差λ/2正交二元波片，二者组合的复合波片具有加工成本低、消色差性能优越的特点；并采用最小阻尼二乘法进行全局优化，设计出了可见光波段具有实际运用价值的二分之一消色差波片。

1 设计原理

1.1 正交二元消色差波片结构和原理

波片是由单轴双折射晶体材料制作而成，其中寻常光（o光）和非寻常光（e光）以不同速度行进，二者产生一个相位延迟，其光程差为

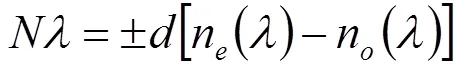
通过波片后o、e光波的相位延迟量为

假设A代表石英，B代表氟化镁，两晶体组成的正交二元复合波片结构如图1所示，并假定在波长1和波长2处具有相同的延迟量，即对这两个波长消色差，则两晶体的厚度a，d分别为：

（4）

式中为相位延迟量的级数，△n1a，△n1b，△n2a，△n2b分别为两种晶片在波长1和波长2处的双折射率。（3）式、（4）式分别给出了在不同波段（1-2）及不同相位延迟量的情况下，所对应的制作消色差波片材料石英和氟化镁的厚度。若解出的两波片厚度同号，则令两波片的快轴相互平行，若两波片的厚度异号，则令两波片的快轴相互垂直。这样的波片组合就能达到消色差的效果。但从公式来看，明显能够知道只有在1，2两个波长点处，消色差波片才会达到要求的延迟量，在其它的波长处延迟量就会有所偏差。因此采用以上的方程求解到的两波片组合，只是粗略的厚度值并不能用于产品的生产。这就涉及到消色差波片延迟精度的问题，延迟精度是衡量消色差波片的一个重要指标，延迟精度越小消色差的性能就越好。必须经过全局优化出最佳厚度才能找到延迟精度最小的消色差波片组合。

1.2 正交二元消色差波片的优化设计

以厚度分别为a，d的石英和氟化镁组成的二元复合波片在波段（1-2）范围内的相位延迟量为

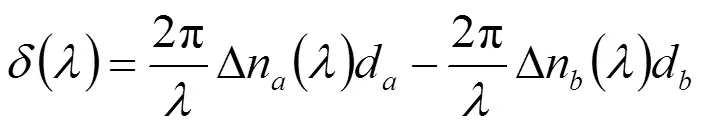
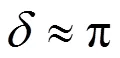
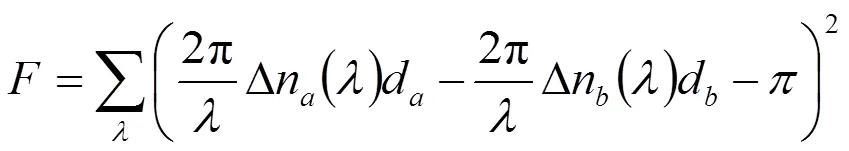
评价函数可体现消色差波段中每一波长的重要性，其值为将消色差波长范围内的波长以5 nm为间隔来求和而得，通过最小二乘曲线拟合技术进行优化[8]，当取值最小时对应的解即为最优石英和氟化镁厚度组合。

消色差波片是对双折射率极其敏感的一种器件，在整个的优化过程中，消色差波片材料的色散方程的选择是极其重要的。选取可见光波段与实际较为符合的石英和氟化镁材料的色散方程进行优化。石英色散方程为[9]：

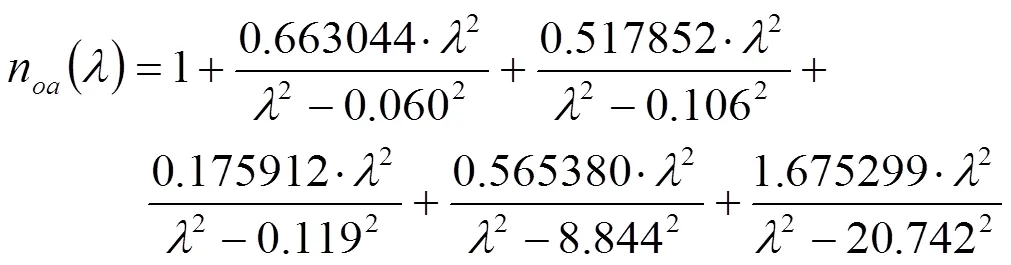
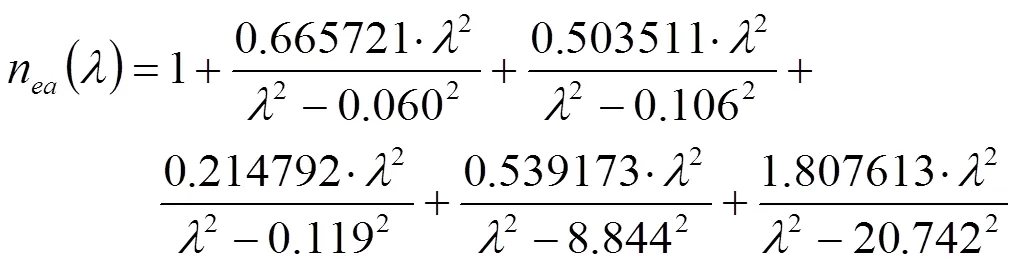
氟化镁的色散方程为[9]：

其中波长单位均为微米。

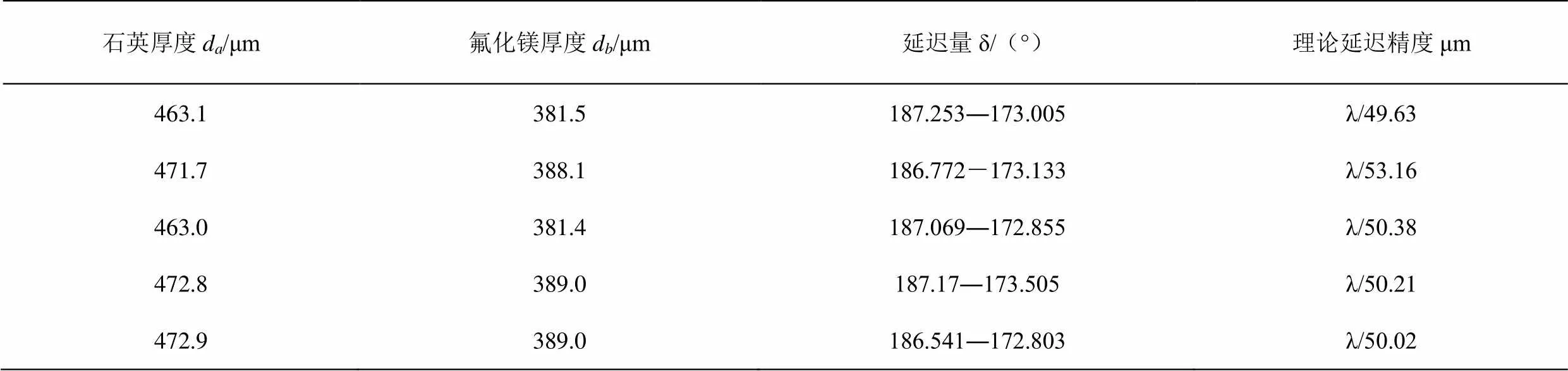
表1 正交二元消色差λ/2波片厚度组合

表1中延迟量 δ 表示该设计组合的消色差波片在波段440 nm-665 nm能产生的位相延迟范围，延迟精度为 δ 偏离理想延迟量 π 造成的程差延迟的波长表示。

把以上组合1设计参数代入式（5），利用matlab软件绘制出相位延迟量δ随波长λ变化的理论曲线图，如图2所示，可以看出该组合厚度的复合波片具有较好的消色差性能，其延迟量最大偏差到187.253度与173.005度，即延迟偏差最大为7.253度，折算成波长表示的程差延迟为 λ/49.63，延迟精度接近 λ/50，满足设计的要求。

图2 消色差特性曲线图

2 实验测试

2.1 测试原理

不论是在消色差波片的制作过程中还是制作好后，检测都是不可或缺的一个重要步骤。目前波片延迟量的检测方法有很多种，主要有光学补偿法、分频激光探测法、电光补偿法、机械旋光调制法、半阴法等[10-13]。本文采用谢奈尔门补偿法[15]测试复合波片的相位延迟，实验光路如图3所示。

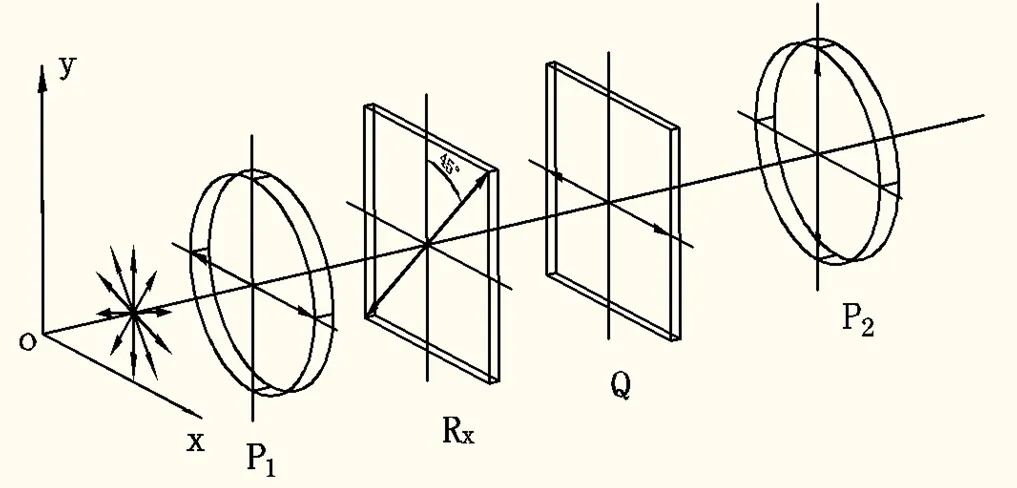
图3 实验光路图

在测试光路中光源为一波长可调光源，Q为光源对应波长的1/4补偿片，其快轴沿x轴，两个偏振器P1、P2正交，P1偏振化方向沿x轴，P2偏振化方向沿y轴，Rx为待测消色差波片，其方位为与x轴成45度。光源发出的光经第一个偏振器P1后变为直线偏振光，然后通过方位为45度的待测波片变为椭圆偏振光，当此椭圆偏振光通过快轴方向沿x轴的1/4补偿片Q，受到1/4波片的相位补偿后又变为一线偏振光，此时可通过检偏器P2检测消光方位，这时检偏器转过的角度θ为待测波片相位延迟 δ 的一半，即

δ=2θ （11）

我们称θ为延迟半角，利用式（11）从旋转角 θ 即可求出待测波片相位延迟量的大小δ。

下面对上述实验检测方法进行一下定量分析，经由偏振器P1出射的线偏振光的Jones（琼斯）矢量为

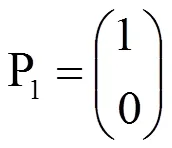
延迟量为 δ 的待测波片，其快轴与ox轴相交45o角，则它的Jones矩阵为

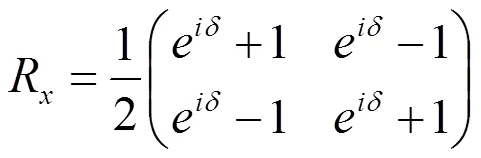
快轴沿ox方向的1/4波片的Jones矩阵为

则从1/4波片出射的光束的Jones矢量为

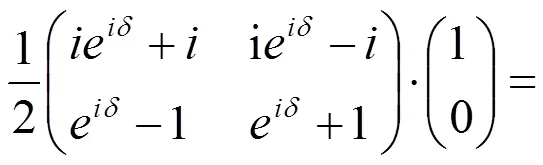
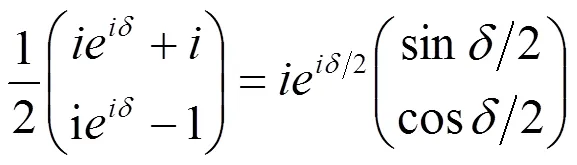
由上式表明，从1/4波片出射的光是一与x轴夹角为 δ/2的线偏振光，旋转检偏器P2使得暗视场重新出现，这时旋转角 θ=δ/2。

2.2 测试结果

测试时在消色差波段内选取几个波长点（实验中选取测量波长为0.44、0.46、0.48、0.532、0.6、0.6328、0.665微米的七个点），调整光源波长至对应波长点，并选取与光源波长相对应的1/4波片分别进行测量，确定消色差特性曲线。图4中曲线为理论设计的消色差特性曲线图，圆点代表实验测量值。由图可见测试结果与理论值接近，其延迟精度可达 λ/50，证明了复合消色差 λ/2波片设计理论的正确性，具有一定的实际参考价值。

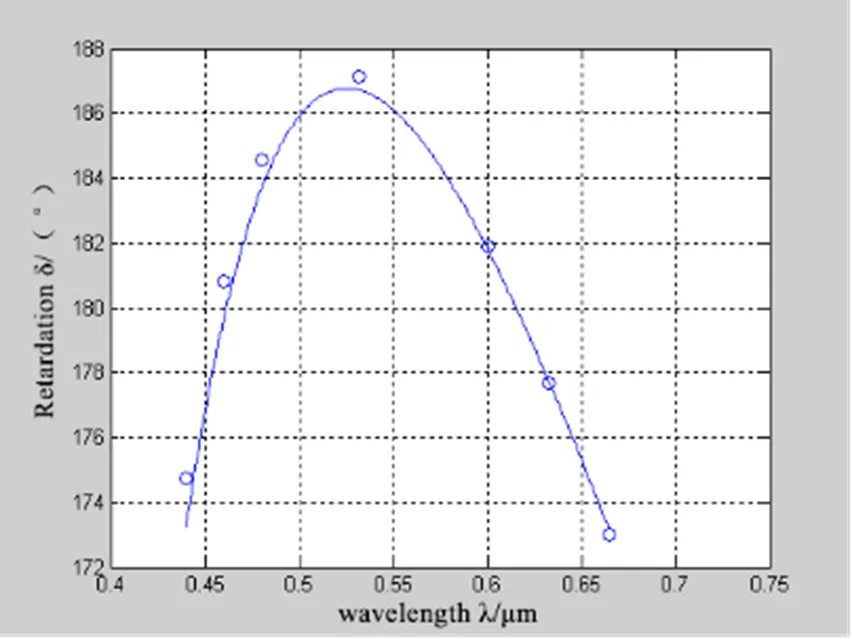
图4 理论消色差曲线与实际测量值对比图

2.3 误差分析

由图4可看出实验测量值与理论设计的消色差曲线存在一定的误差，这些误差主要是由系统误差、测量误差及器件误差引起的[15-16]。例如，测试光源不稳定性及其波长调节的精度等，复合波片材料双折射率测量误差、多级波片的厚度误差造成，测量环境中杂散光的影响，消色差波片的方位角效应、温度效应等都会给实验带来一定误差。

3 结论

用石英和氟化镁材料组合方式设计消色差波片不仅简单，而且调整使用灵活方便。本文根据复合波片理论，并通过最小二乘曲线拟合优化设计方案，设计出了可见光波段消色差二分之一复合波片。理论研究和实验检测结果均表明，采用本方案设计出的消色差二分之一波片技术指标是可行的。

[1] 廖延彪．偏振光学[M]．北京:科学出版社,2003:263-343.

[2] 谷洪刚. 宽带复合波片优化设计与性能表征方法及其应用研究[D]. 武汉:华中科技大学,2016.

[3] 王荣新,宋连科,杨海磊. 1300nm-1600nm消色差四分之一波片的二元设计[J].激光杂志,2014,3(2):26-27.

[4] 郭丽娇,吴福全,宋连科,等.用模拟退火算法设计的云母λ/2消色差复合波片[J].中国激光,2010,37(6): 574-1578.

[5] 郑春红,宋连科,梁荣饶.三元复合式消色差λ/4波片的优化设计[J]．中国激光,2004,31(6):662-664.

[6] 岳增友,吴福全,孙丹.双折射晶体相位延迟片的延迟量色散性分析[J]．光学技术,2015,41(5):467-470.

[7] 廖延彪．偏振光学[M]．北京:科学出版社,2003:215.

[8] 薛定宇.基于MATLAB/Simulink的系统仿真技术与应用[M]．北京:清华大学出版社,2000:178-180.

[9] Marvin J, Weber Ph D. Handbook of Optical Materials[M]. California: Lawrence Berkeley National Laboratory, 1932:97,100.

[10] 薛庆文,李国华. 半阴法测量λ/4波片的相位延迟[J]．光电子·激光, 1998,9(2):150-151.

[11] 崔祥霞. 精确测量波片相位延迟量的新方法[J]．光电子·激光,2005,16(2):183-187.

[12] 严明,高志山. 移相法测量波片的相位延迟量[J]．光电子·激光,2005,16(2):183-187.

[13] 李鹏,刘航,张玉红. 一种基于电光调制测量波片相位延迟的方法[J].通信电源技术,2016,33(2):111-112.

[14] 新谷隆一. 偏振光[M]．北京:原子能出版社，1994:40-44.

[15] 岳增友,吴福全,孙丹,等. 双折射晶体相位延迟片的延迟量色散性分析[J].光学技术,2015,41(5):467-470.

[16] 穆廷魁,李国华,宋连科. 石英波片相位延迟随温度的变化行为[J].中国激光,2006,33(7):949-952.

Design of two-element of 440nm-665nm achromatic half-waveplate

HUANG Yan

（Electronic Engineering Department, Zhangzhou Institute of Technology, Zhangzhou, Fujian 363000, China）

In order to design achromatic half-wave plate suitable for visible light band, according to the theory of composite wave plate, quartz and magnesium fluoride materials are selected by using least squares fitting method to design achromatic λ/2 composite wave platein the range of 440 nm~665 nm. Both the theoretical research and experimental results show that the phase delay accuracy of the achromatic λ/2 composite wave plate designed according to this scheme can reach λ/50, which meets the needs of practical use.

applied optics; achromatc; least squares method; composite wave-plate;retardationd precision

O436.3

A

10.3969/j.issn.1674-8085.2019.02.002

1674-8085(2019)02-0006-04

2018-12-26；

2019-01-16

黄 艳(1983-)，女，福建闽清人，讲师，硕士，主要从事光学晶体偏振特性及偏光器件方面的研究(E-mail:huangyan_013@126.com).