相对于余挠对的内射模和投射模
2019-04-09何东林李煜彦
何东林,李煜彦
相对于余挠对的内射模和投射模
*何东林,李煜彦
(陇南师范高等专科学校数信学院,甘肃,陇南 742500)
设=(C,F)是一个完全的遗传的余挠对。给出--内射模和是--投射模的概念,研究--内射模和--投射模的若干性质和等价刻画。
余挠对;--内射模;--投射模
1 预备知识

2 t -子模

3 相对于余挠对的内射模

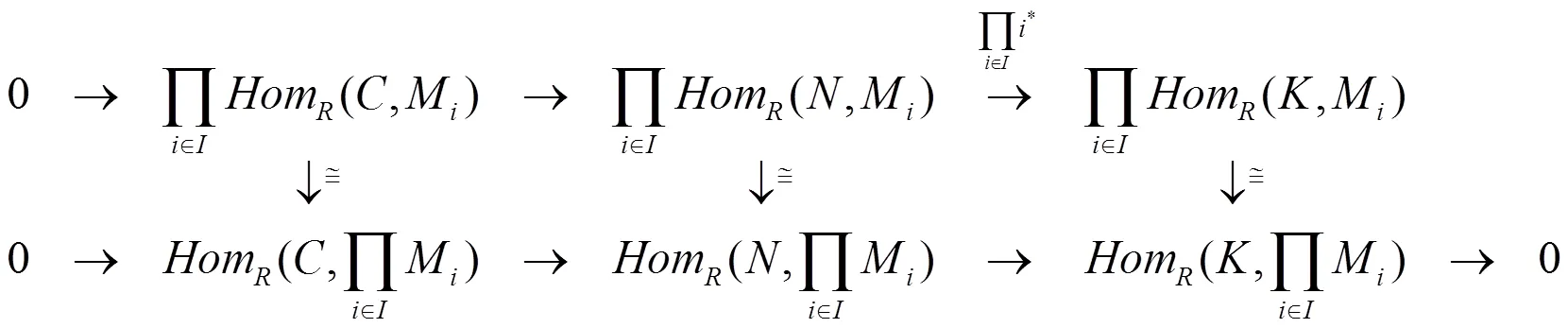
由上面的引理易得如下两个推论。
证明 对任意正合列
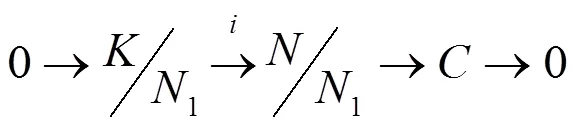

由上面的定理易得如下推论。
4 相对于余挠对的投射模
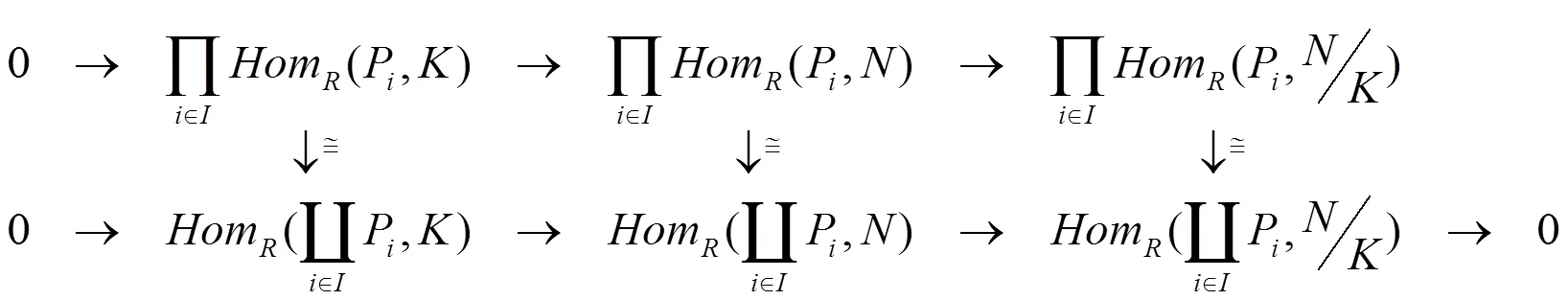

由上面的定理易得如下推论。
[1] Mao L X, Ding N Q. FP-projective dimensions[J]. Comm Algebra, 2005, 33(4):1153-1170.
[2] Mao L X, Ding N Q. Relative projective modules and relative injective modules[J]. Comm. Algebra, 2006, 34: 2403-2418.
[3] Holm H. Gorenstein homological dimensions[J]. Journal of pure and applied algebra, 2004, 189(1-3): 167-193.
[4] Bennis D, Mahdou N. Strongly Gorenstein projective, injective, and flat modules[J]. Journal of Pure and Applied Algebra, 2007, 210(2): 437-445.
[5] Abbas M S. On relative pure injective modules[J]. Al-Mustansiriyah Journal of Science, 2010, 21(6): 374-382.
[6] Wang L. Strongly n-Ding projective and injective modules under change of rings[J]. International Research Journal of pure Algebra, 2017, 7(3): 509-512.
[7] Abbas M S, Hamid M F. Pure Injective Modules Relative to Torsion Theories[J]. International Journal of Algebra, 2014, 8(4): 187-194.
[8] Anderson F W, Fuller K R. Rings and categories of modules[M]. Springer: SpringerScience & Business Media, 2012.
[9] Enochs E E, Jenda O M G. Relative homological algebra [M]. New York: Walter de Gruyter, 2000.
[10] 佟文廷.同调代数引论[M].北京:高等教育出版社,1996.
Injective and projective modules relative to cotorsion pair
*HE Dong-lin, LI Yu-yan
(Department of Mathematics, Longnan Teachers College, Longnan, Gansu 742500, China)

cotorsion pair;--injective modules;--projective modules
O153
A
10.3969/j.issn.1674-8085.2019.02.001
1674-8085(2019)02-0001-05
2018-12-03;
2019-01-26
甘肃省高等学校科研项目(2018A-269),陇南师范高等专科学校校级科研重点项目(2016LSZK01003)
*何东林(1983-),女,甘肃白银人,讲师,硕士,主要从事同调代数研究(E-mail: hdl7979085@163.com);
李煜彦(1983-),男,甘肃西和人,讲师,硕士,主要从事环模理论研究(E-mail: nwnulyy@126.com).
