基于在线信息的群评价模型及其偏序集求解方法

岳立柱， 李良琼

(辽宁工程技术大学 工商管理学院，辽宁 阜新 123000)

0 引言

随着互联网络和电子商务的迅猛发展，消费者给出的在线评价信息迅速增长。这些资料在未经过处理与分析前，无法作为参考或是辅助决策的依据，但只要经过恰当的处理与分析就能将巨量资料转化创造出价值与应用[1]。近20多年，国内外学者对在线评论进行了大量而深入的研究，但由于数量巨大、多样性、动态性等特征，学者Chen[2]等认为提取产品评论信息仍然存在很大阻碍。对大数据信息如何进行有效集结，至今仍有待研究。对于大数据的集结问题， Pfeiffer等认为[3]多准则决策分析方法在一定程度上获得了更大的接受度，因为它能结合来自不同来源和不同类型的数据。不过，在线评价信息已经超出了传统多属性群决策理论的应用边界。

在线评价信息的研究已经取得很多成熟的成果，但从多准则决策视角探索实践应用的文章非常缺少。评价数量影响销售方面，Chen等[4]认为消费者在线评论的数量反应了商品受欢迎的程度，在线评论数量越多，潜在消费者关注该商品或服务的可能性越大。Dellarocas等[5]实证发现某在线产品或服务的评论数量越多，消费者做出消费决策的机会就越大。Duan等[6]研究发现产品的前期评论数量影响当期的收入，也就是说前期评论数量对以后该产品或服务的收入有影响。评价打分影响销售方面的研究取向，已经从平均打分转向极性分析，即是正面的、中性的和负面的评价研究对销售的影响。Liu等[7]研究表明正向的评价对商品交易量有显著的积极影响，负向的评价对商品交易量有显著的消极影响，中立评价无显著影响。郝媛媛等人研究表明只有5星评价和1星评价的评论数对电影票房的影响比较显著，其它星级影响不大[8]。另外，还有学者发现产品的价格越高，评论对销量的影响越大[9]。上述在线评论的研究主要集中于影响销售机制与因素的研究，有关产品排序比较和产品市场结构的研究比较鲜见。文[2]在相关语言计算、TOPSIS模型基础上提出了产品市场结构的WVAP分析方法；习扬和樊治平[10]率先研究了在线群评价模型的求解方法，将决策矩阵中的向量用离散型概率分布函数形式来表示，并构建加权累积分布函数决策矩阵。进一步地，通过构建确定属性权重的优化模型并对模型进行求解。在涉及数据集结过程中，相关研究都要依赖权重进行集结。在多准则决策中权重体现了偏好顺序，但研究早已表明群体偏好具有不一致性，加之，无论个体和群体偏好也处于变动之中，因此，用唯一一组权重进行准则集结在理论上是困难的。另外，通过群体评价信息进行个性化推荐时，需要咨询者提供权重信息，实际上大多数人不明白权重的意义，故如上方法是不能进行个性化产品推荐的。为了克服权重不能精确获得的问题，采用一种非参数的决策方法即偏序集决策方法。

在线群决策评价矩阵较传统群决策评价矩阵发生了显著变化，即矩阵中的每个元素不再是单值实数，而是一个多维向量。例如，对某款SUV汽车外观评价进行统计，有60%用户认为很好、有30%用户认为一般，有10% 用户认为较差，该款车外观属性评价值为向量(0.6，0.3，0.1)。当准则取值为向量时，如何对多个向量进行集结？国内外一些学者，研究了传统群决策比较关系矩阵。Herrera[11]拓展了比较关系矩阵，元素从实数拓展为向量(称之为向量比较矩阵)，采用均值算子对语义向量进行集结。为了解决现有的单等级上的比较关系，不能同时表达多种不同偏好关系的问题，提出一种新的基于多等级方案成对比较的决策方法，构建方案集上基于对称框架的分布式多等级偏好关系[12]。针对方案集提供的两两方案比较偏好信息是基于语言短语集来描述的(实际上相当于语言向量)，利用 OWA 算子将每个决策者的偏好信息集结成为群的比较偏好矩阵[13]。Chiclana等[14]，Wu和Cao[15]提出了一些诱导的有序加权平均算子，并将其应用于模糊偏好关系的群集成问题。这些方法适用于传统群决策，由于在线群决策评价者数量过多，且存在大量“残缺”赋值的问题，难以得到单个人的比较矩阵，自然无法综合得到总体的比较矩阵，但为在线群决策研究提供了思维试验基础。文[10]得到了语言评价向量的比较矩阵，但没有对进行两极问题进行研究，不仅正负评价的影响不同，Adomavicius (2005)认为用户评分数据是一种并不很有代表性和无偏的样本数据，因为大多数情况下用户只对自己喜欢的商品进行评分[16]。本文采用两极评价方式即将评价向量“拆分”为正向评价和负向评价两个向量。针对权重问题采用偏序集的方法来进行求解，实现通过权重顺序不需具体数值便能对向量进行集结和比较，进而实现方案比较与个性化推荐。

1 在线群评价模型

1.1 在线群评价模型概念

用户在线评论这一宝藏主要以自然语言表述的文本形式分散地存储在各种类型网站上，为了能够使用户评论信息被推荐系统利用，首先需要将分布存储的用户评论收集起来。文[10]给出了由语义数据提取结构化信息的一般形式：

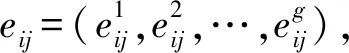
用户在线评价是一种特殊的群决策问题，与传统群决策研究对象相比主要有五方面差异：(1)评价群体人数相差悬殊。在线评价者人数众多，常以万计，传统评价人数较少，一般控制在几十人以内；(2)信息完备程度差异明显。在线评价者往往对自己了解或感兴趣的属性进行赋值，一般对产品体验越强烈，发布评论的动力越大，当用户没有使用体验，或体验一般时发表较少的评论，传统评价者往往是相关领域的专业人士，对方案所有属性无论自身是否感兴趣，都要按固定的规则给出评分；(3)群体相互影响方式不同。网络评价中先行的评价会对后续评价产生影响，后评价者不会对前评价者产生影响，评价者之间一般不会进行面对面交流，而传统群决策经常需要进行相互的了解和沟通，有时决策者之间通过互动反馈的方式产生影响；(4)评价群体固定性不同。网络评价主体是开放式的，每个利益相关者或者体验者都可以是评价主体，评价人群规模处于动态变化之中，传统群决策评价者人员相对固定，当评价完成后，群体一般解散；(5)赋值方式有所不同。前者多为语义信息评价，后者往往采用数字打分方式，即使应用语义也遵守相同的语义粒度。综上，群体特征和评价方式上的差异，最终导致了在线群评价模型与传统评价模型相比发生了质的变化。

围绕“线上”特征，根据引言文献的相关结论，给出线上评价模型需要满足三个假设条件：(1)评价者数量众多且单个评价者对群体评价不产生决定性影响；(2)正向评价对于未来决策者具有正向影响，负向评价对未来决策具有负向影响；(3) 每个人都是对自己体验深刻的内容评价，不了解内容不进行评价。 假设1规定了该评价是一个群评价，单个评价者不能起到决定性作用，否则，称不上是真正意义的群评价。 假设2表明网络评价的特征，现有评价会向其它人群扩散，评价具有后继影响，反映了评价的持续性和动态性。假设3表明评价的有偏性，表明获取的评价向量的概率分布是有偏的。

1.2 评价向量的拆分

用户评价呈两极分布[16]，因此向量的概率分布是有偏的，即正负两极的评价比例偏大，而中性评价比例偏小。 根据假设(2)可知正负两极的评价影响是不同的，因此将原向量拆分为正向评价向量和负向评价两个向量。为表示方便，设语言标度g=2k+1，即语言标度向量(L-k,L-k+1,…,L0,…,Lk-1,Lk),。便于分析，规定语言标度Li，若下标t取值为正数，表明是正向评价，数字越大表明正向评价水平越高。若下标t取值为负数，表明是负向评价，绝对值越大表明负向评价水平越高。若下标取值为0，表明是中性评价。

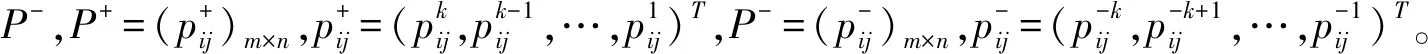
1.3 方案排序

设方案属性权重为ω1,ω2,…,ωn,对于第i个方案正、负向评价向量的综合向量分别为

(1)

(2)

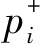
上述排序思路与传统方式比较类似，但在应用中获取权重总是困难。类似地应用文[10]方法获得权重，虽然能反映群体属性偏好，但无法为客户提供个性化推荐，因为客户个人偏序往往是有差异的。例如，公司白领购车可能注重品牌和舒适度，而农村购车者可能更关注价格和空间。获得在线数据属性权重具有极大困难，一是评价信息不全且有偏，客观赋权法很难适用；二是数据量巨大，客户群体往往多样且动态变化，这经常超出了专家的认知范围。精确权重很难获得，退而求其次，获得准则的权重顺序，在偏好序列基础上，应用偏序集相关理论进行排序分析和个性化推荐。

2 偏序集决策分析方法

2.1 偏序集基础概念

定义1[17]设R是集合A上的一个二元关系，若R满足

(1)自反性：对任意x∈A，有xRx；

(2)反对称性(即反对称关系)：对任意x,y∈A，若xRy且yRx，则x=y;

(3)传递性：对任意x,y,z∈A，若xRy且yRz，则xRz。

则称R为A上的偏序关系。

在应用中，通常用“⪯”表示偏序关系，集合A和其上的偏序关系⪯一起称为偏序集，记为(A,⪯)。本文约定“⪯”表示为：对∀x,y∈A，有

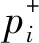
(3)

其中

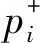
(4)

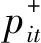
(5)

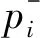
(6)

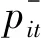
(7)

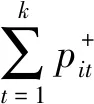
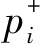
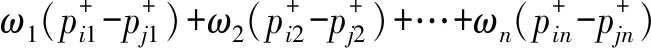
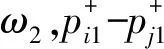
故设取前k个元素时有

于是，对于前n个准则表达式有

由题设知

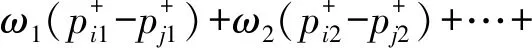
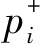
从矩阵运算视角，定理1可以用两个矩阵P+和I直观描述，其中I为n维上三角矩阵，即

S+=P+·I的表达式为块矩阵

(8)

在块矩阵S+中，若第i行块向量大于第j行块向量，则说明正向评价方案ai优于方案aj。通过定理1可知，只要权重秩次不变，无论具体取值如何变化，两个可比方案的比较关系不变。矩阵S+每个元素都是一个k维列向量，对两个k维向量的比较，由定理1可有如下推论。

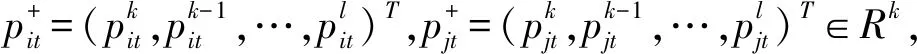
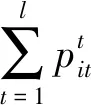
(9)

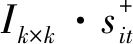
H·S+=H·P+·I

(10)

其中，H为分块对角矩阵，O为k阶零矩阵。

矩阵H·P+·I为块矩阵，若第i行块向量大于第j行块向量，则可知正向评价方面aiaj。

对于负向评价集M-=(A,IC,P-)，同理可得

H·S-=H·P-I

(11)

矩阵H·P-·I为块矩阵，若第i行块向量大于第j行块向量，则可知负面评价方面ai高于aj。显然，若矩阵H·P+·I第i行块向量大于第j行块向量，H·P-·I第i行块向量小于第j行块向量，则可知aiaj。

2.2 方案排序与Hasse图生成方法

定义2给定评价集M=(A,IC,P)，对于∀ai,aj∈A，若aiaj时有rij=1，若aiaj时有rij=0，则称R=(rij)m×m为评价集M的比较关系矩阵。

传统群决策方法，根据比较关系矩阵对方案进行比较排序。通过比较关系矩阵可以看出，第i行之和表示了第i个方案优于或等于其它方案的个数，该值越大表明方案程度越优;第i列之和表示了第i个方案劣于或等于其它方案的个数，该值越小表明方案程度越优。因此，在这两点特征基础上构造排序方法：

(12)

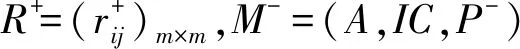
(13)

偏序集决策方法与此不同在于，不仅可以通过比较关系矩阵对方案进行排序，还可以借助Hasse 图对方案进行分析。由比较关系矩阵得到Hasse矩阵，由Hasse矩阵得到Hasse 图。文[19]给出了比较关系矩阵与Hasse矩阵相互转化的关系：

HR=(R-I)-(R-I)2

(14)

其中，R为关系矩阵，HR为Hasse矩阵，i为单位矩阵，矩阵(R-I)2为布尔运算(即1+1=1，1+0=1，0+0=0，1×1=1，1×0=0，0×0=0)。 需要说明的是，应用式(14)不允许出现雷同方案。

由Hasse矩阵可以绘制Hasse图(关于Hasse图详细绘制介绍可参见文[20])。Hasse图直观地反映了方案间的结构信息，对同层元素而言，层内的方案是不可以直接比较的，这些方案的排序顺序会随着权重向量的变化而变动，揭示了方案排序的非确定性；对于图中可比较优劣的方案，表明权重大小无论怎样变动，只有权重大小顺序不变，则方案间的比较关系不变，揭示了方案排序比较的稳定性。

2.3 操作步骤

第一步：根据权重由大到小的顺序，将指标从左至右进行排列，得到调整后的向量评价矩阵P，将P“拆分”为正向评价矩阵P+和负向评价矩阵P-；

第二步：根据权重大小信息，按定理1得到P+·I和P-·I；

第三步：根据语义标签的重要程度，根据推论1得到H·P+·I和H·P-·I；

第四步：若H·P+·I第i行块向量大于第j行块向量，若H·P-·I第行块向量小于第j行块向量，则有rij=1，否则rij=0，于是得到比较矩阵R=(rij)m×m；

第五步：根据式(13)进行排序，由式(14)得到Hasse矩阵，绘制Hasse图，进行结构分析。

3 实例对比分析

文[2]利用网络爬虫技术从汽车之家网站获得如上5款汽车8个指标的评价信息。汽车之家网站给出了8个影响汽车购买的指标: 空间(C1)、动力(C2)、操控(C3)、油耗(C4)、舒适性(C5)、外观(C6)、内饰(C7)和性价比(C8)。根据用户在线评价信息，对吉普指南者(A1)、马自达CX5(A2)、斯巴鲁森林人(A3)、丰田汉兰达(A4)和雪佛兰科帕奇(A5)等5款SUV汽车进行排序， 以便对潜在的汽车购买者提供服务与决策支持。语言评价标度集为L={l-2,l-1,l0,l1,l2}，其中，l-2表示最差，l-1表示较差，l0表示一般，l1表示较好，l2表示最好。在计算过程中，重点展示正向评价矩阵的转换过程。

第一步：按照文[10]权重顺序ω1>ω6>ω2>ω8>ω5>ω3>ω1>ω4,得到评价向量矩阵(数据源见文[10]表1)，将评价向量矩阵“拆分”为正向评价矩阵P+(见表1)和负向评价矩阵P-(表略)

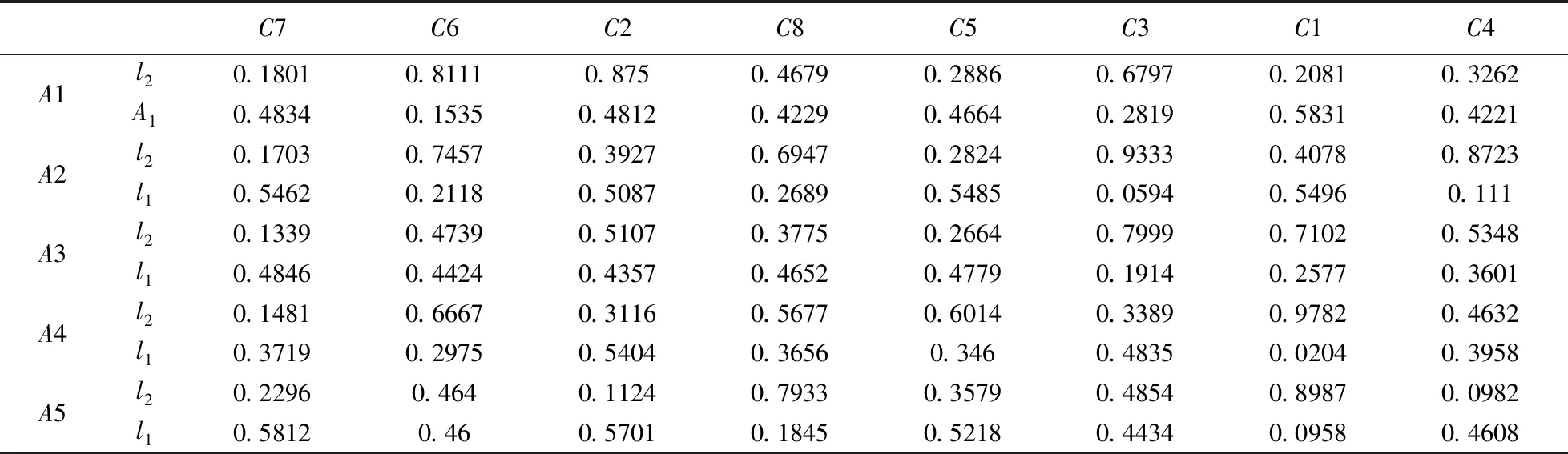
表1 正向评价矩阵

第二步：根据权重秩次信息应用定理1，P+左变换得到S+=P+·I(表2)

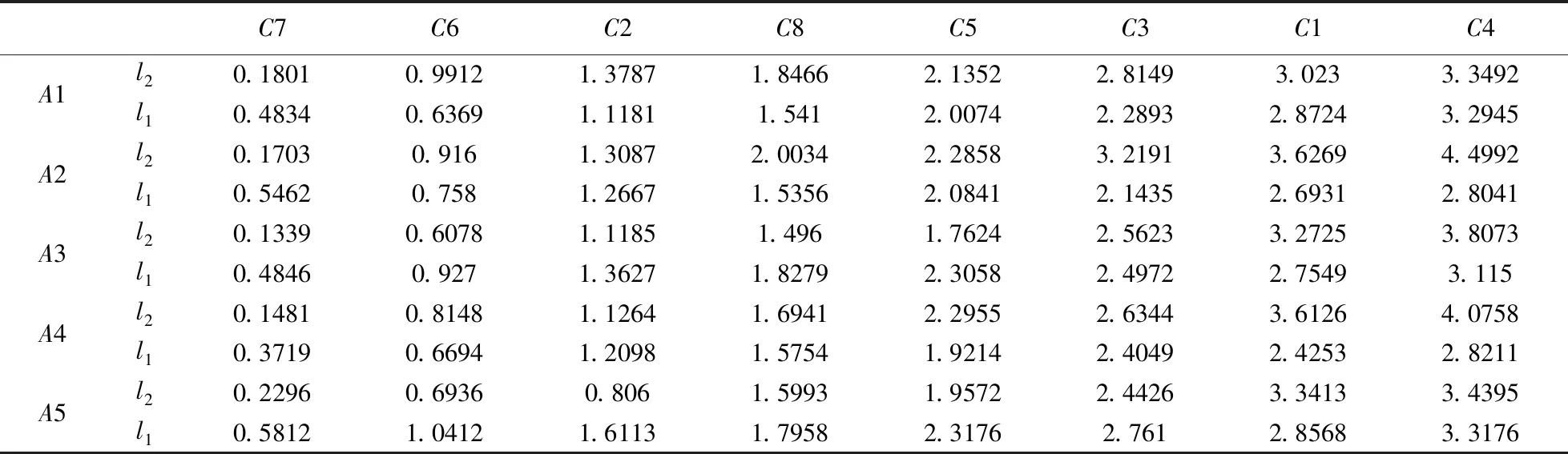
表2 列变换正向评价矩阵

第三步： 根据语言标度的重要程度，根据推论1对矩阵S+进行左变换，得到H·S+=H·P+(表3)

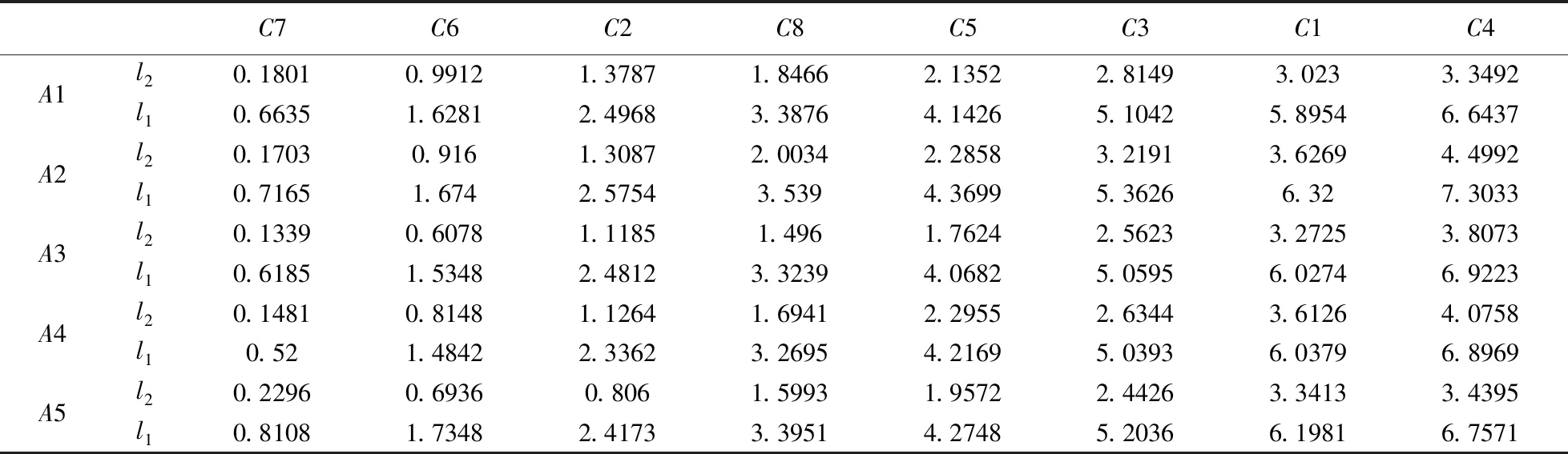
表3 行列变换正向评价矩阵

第四步：根据H·P+·I第i行块向量大于第j行块向量的比较，得到正向评价矩阵的比较关系矩阵

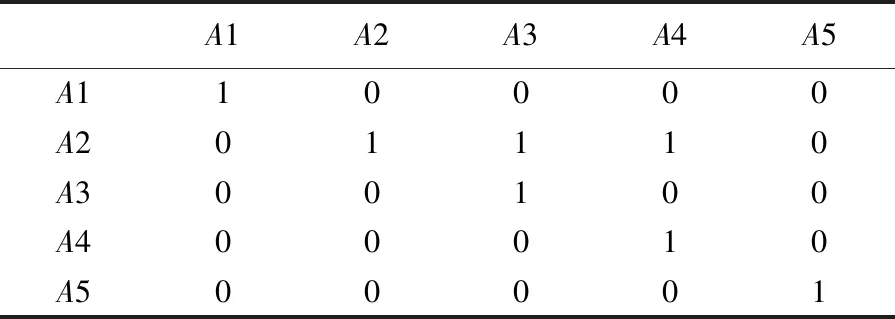
表4 正向比较关系矩阵

第五步：由式(12)得到5款SUV汽车排序结果为A2A5=A1A3=A4,由式(13)φ(A1)=(1+1)/(1+2)=2/3,φ(A2)=3,φ(A3)=3/4,φ(A4)=1/3,φ(A5)=2,得到5款SUV汽车排序结果为A2A5A1北A3A4,由此可见，式(13)的排序能力强于式(12)。根据式(14)得到正向比较矩阵的Hasse矩阵，根据该矩阵绘制Hasse图；与此类似，也可以得到负向比较矩阵的Hasse图。结果分析：

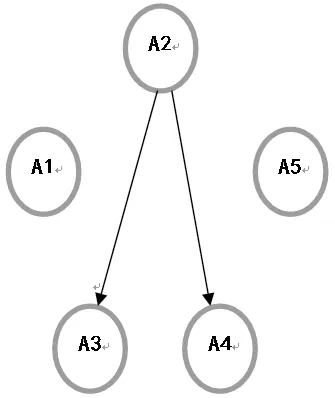
图1 正向评价矩阵Hasse图

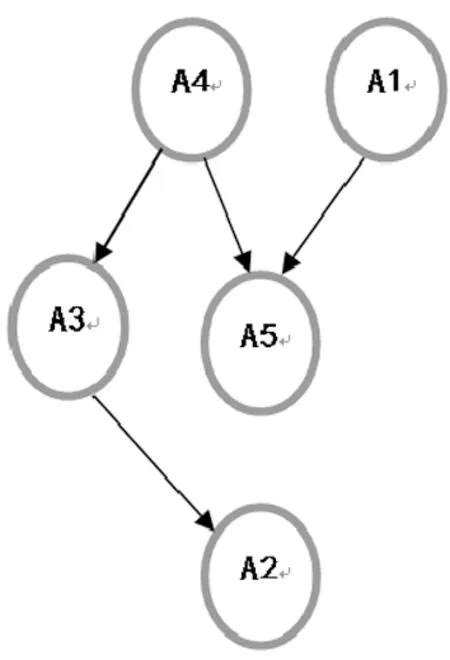
图2 负向评价矩阵Hasse图

(1)由正向评价矩阵对应的Hasse图可以看出，A1、A2和A5无法相互比较，表明三款SUV在8项指标方面各有所长，例如A1在外观方面(C6)评价最好、A2在操控(C3)和油耗(C4)方面评价最好；A5在空间(C1)和性价比(C8)方面评价最优。A3和A4正向评价指标均劣于A2，A3和A4两款车在巩固和扩展客户上，面临着严峻挑战。由于A1、A2和A5三款车各有独特卖点，这三款车会保持各自的目标市场，但A2市场有所扩大，有吞并A3和A4的发展趋势。

(2)由负向评价矩阵对应的Hasse图可知，A4和A1的负面评价最高，表明这两款车的口碑最差，A2的负面评价水平最低，说明该款车负面评价相对最少。

(3)A2正面评价高于A3和A4，同时负面评价又低于A3和A4。进一步肯定了，A2呈扩展之势，能够吞并A3和A4的市场，即A3和A4市场呈萎缩态势；A1和A5能够维持已有市场份额，A1负面评价过高、缺点共存，不具备向其它市场拓展的实力。

结果对比：

(1)虽然文[2]给出了5 款SUV汽车的排序值结果，但对于企业来说更关注竞争产品和市场结构的变化。在给定偏好结构不变的情况下，本文发现整个市场呈三足鼎立的态势：A1，A2和A5各占据偏好不同的客户，其中A2有吞并A3和A4的趋势。这说明，通过Hasse图中结构关系，能够反映研究对象间的结构性关系，而不是简单的一排了之。通过比较5 款SUV汽车的排序值可得到排序结果为A2≻A1≻A4≻A5≻A3。

(2)本文的方法不需要具体的权重值，只需权重的秩次，这为实践应用带来方便．任给一组权重，只要权重顺序不变，则方案集可比较关系不变，免去了权重仿真过程。

(3)对于消费者而言，不同的人偏好结构并不相同，只要消费者给出指标的全部或部分偏好顺序，通过本文方法根据采集的信息对消费者推荐车型。解决了文[2]不能进行个性化推荐的难题。

4 结论

应用向量群评价模型能够更为合理地表示群体的网络评价信息。对于采集得到的向量评价矩阵，从正向和负向两个评价维度对应拆分两个维度。在权重顺序可辨而大小未知的条件下，应用偏序集能够对方案进行比较．通过两两方案比较，由比较矩阵可得到Hasse矩阵，再由Hasse矩阵绘制Hasse图，通过该图能直观地对方案进行归类和分层。对企业来说，通过产品的评价Hasse图，能够分析竞争产品和本产品的优劣情况，观察市场的结构变化，对于网站而言能够对用户进行个性化推荐。该方法具有概念清晰、计算简单和易于应用软件实现等特点，为解决现实中基于多属性在线评价信息的方案排序问题提供了一种新途径。