基于时间尺度的离散分数阶Hamilton方程

宋传静

（苏州科技大学 数理学院，江苏 苏州215009）

1937 年，Fort[1]首次引入离散变量微积分理论。基于该理论，具有Caputo 型的分数阶差分算子得以建立并被应用于求解某些差分方程[2－3]。除此之外，离散变量微积分的一些重要结果被整理收集在文献[4]中。考虑到微分方程离散序列的重要应用[4－5]及学者们对连续型分数阶变量微积分的密切关注[6-18]，Bastos[19]在2012 年对分数阶离散变量微积分进行研究。基于文献[20－21]，Bastos 引入了左右Riemann-Liouville 型差分算子，给出了分数阶分部求和公式，并建立了具有左右Riemann-Liouville 型差分算子的离散分数阶Lagrange 方程。最近，文献[22]建立了具有左右Riemann-Liouville 型差分算子的离散分数阶Birkhoff 方程，文献[19]的结果为其特例。因为Hamilton 系统在非线性科学发展中具有重要作用，所以笔者利用等时变分原理分别在有边界条件及无边界条件下，建立具有左右Riemann-Liouville 型差分算子的离散分数阶Hamilton方程。

1 预备知识

这里简单回顾时间尺度和分数阶微积分的定义及相关性质，详细请参考文献[19，23]。

时间尺度T 是实数集的任意非空闭子集，因此，整数集Z 和实数集R 都是时间尺度的例子。

设T 为一个时间尺度，则向前跳跃算子σ：T→T 和向后跳跃算子ρ：T→T 分别定义为

文中，fσ（t）=f（σ（t）），fρ（t）=f（ρ（t））。对于给定的时间尺度T，若sup T＜∞，则Tk=T（ρ（sup T），sup T]；若sup T=∞，则Tk=T。特别地，若a，b∈T，a＜b，用区间[a，b]表示[a，b]∩T，显然，[a，b]k=[a，ρ（b）]。

设f：T→R，t∈Tk，若∀ε＞0，∃N=（t-ω，t+ω）∩T（ω＞0）使得

对于所有的u∈N都成立，则称fΔ（t）为f在t点的delta 导数。

注1如果T=R，则对于任意的t∈R，σ（t）=ρ（t）=t，fΔ（t）=f′（t）。如果T=Z，则对于任意的t∈Z，σ（t）=t+1，ρ（t）=t-1，fΔ（t）=Δf（t）=f（t+1）-f（t）。

设a∈R，b=k+a，k∈N 且k≥2。文中的讨论在时间尺度T＝{a，a+1，…，b}上进行。设α，β 为两个任意实数且α，β∈（0，1]，令μ=1-α，v=1-β。文中，Δf（t）=fσ（t）-f（t）。

对于任意的x，y∈R，x（y）=Γ（x+1）/Γ（x+1－y），其中Γ 为gamma 函数。对于c∈T，成立

左分数阶求和及右分数阶求和定义为[19]

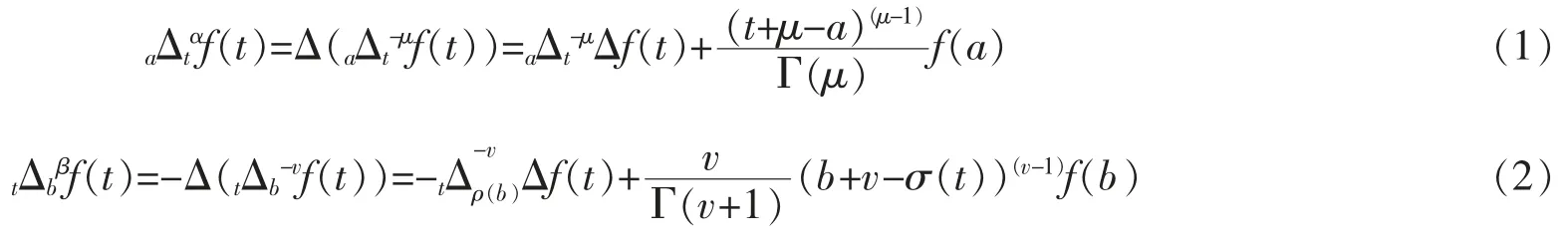
其中

特别地，有

分数阶分部求和公式为[19]

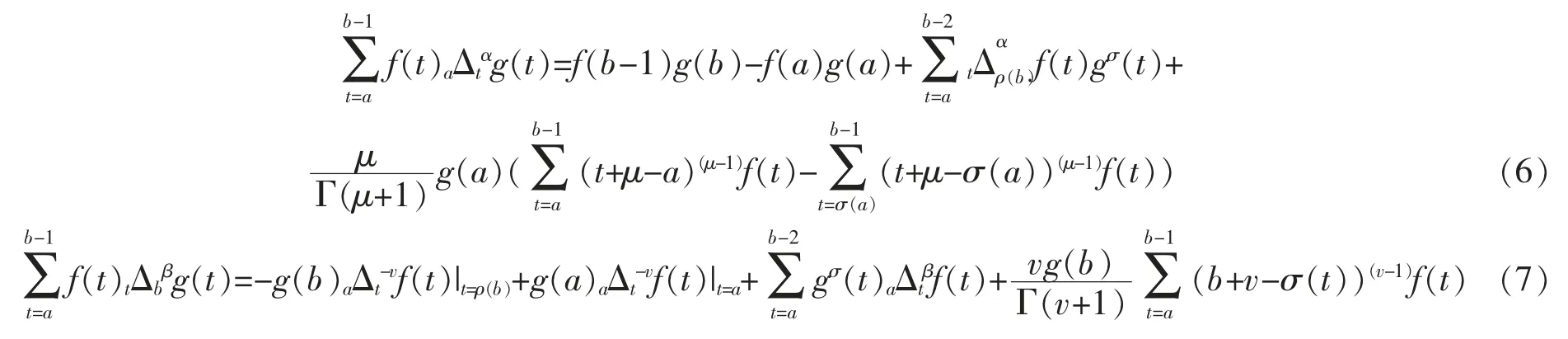
2 离散分数阶Hamilton方程

设q为力学系统的广义坐标，和

称为具有左右Riemann-Liouville 型差分算子的离散分数阶Hamilton 作用量。其中为具有左右Riemann-Liouville 型差分算子的Lagrange 函数。

满足端点条件

和交换关系[24]

的等时变分原理

称为基于时间尺度的离散Hamilton 原理。

引进广义动量和Hamilton 函数

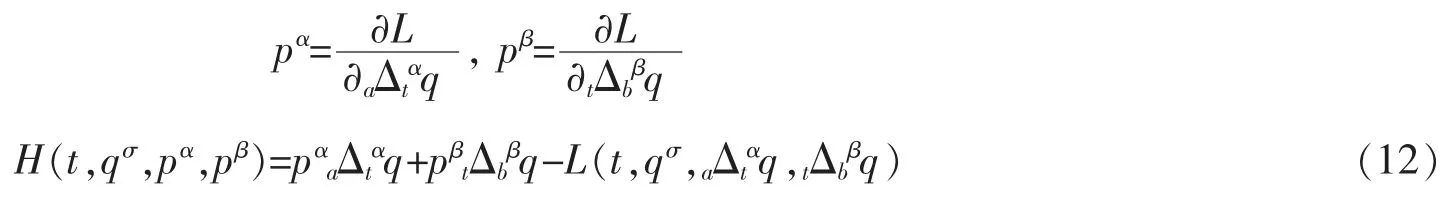
此时，（8）式可写为

且（11）式变为

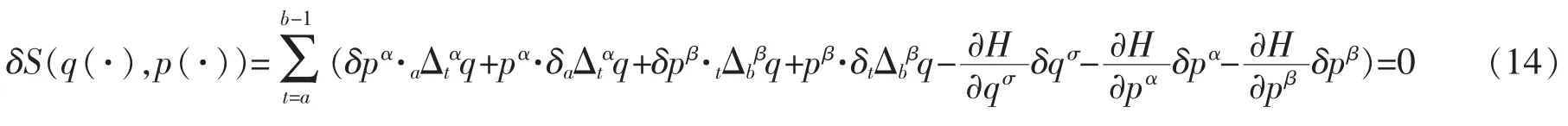
其中

将（9）式、（15）式和（16）式代入（14）式可得

又由（12）式可得

将（18）式代入（17）式可得

由δqσ的任意性得

方程（18）和（20）称为具有左右Riemann-Liouville 型差分算子的离散分数阶Hamilton方程。

注2文中所得的具有左右Riemann-Liouville 型差分算子的离散分数阶Hamilton方程（18）和（20）与文献[22]结果一致。不同之处在于：笔者是通过Hamilton 原理得到的；而文献[22]是作为一个特例得到的。

注3当端点a处没有限制条件（9）时，若想得到具有左右Riemann-Liouville 型差分算子的离散分数阶Hamilton方程（18）和（20），则需要增加一个补充条件

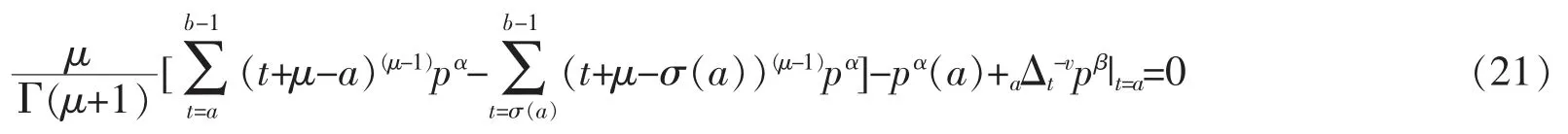
同理，当端点b处没有限制条件（9）时，若想得到具有左右Riemann-Liouville 型差分算子的离散分数阶Hamilton方程（18）和（20），需要增加的补充条件为

注4若Lagrange 函数中只含有左Riemann-Liouville 型差分算子，此时的离散分数阶Hamilton方程变为

在（23）式中令α=1 可得

方程（24）为经典的离散Hamilton方程[25]。

3 算例

研究离散的分数阶Emden 问题，其中Lagrange 函数

由（18）式和（20）式可得离散分数阶Hamilton方程为

（26）式中，令α=1 可得

（27）式与文献[25]所得结果一致。

4 结语

建立了具有左右Riemann-Liouville 型差分算子的离散分数阶Hamilton方程。当α=1 时，可得经典的离散Hamilton方程。基于此文，进一步的课题，如离散分数阶对称性与守恒量，也值得研究。