重视性质,提高解题效益
2019-04-09宁夏银川一中周天佐
■宁夏银川一中 周天佐
同学们在解题过程中,一般采用常规方法,即通法去解决。但有一些题目,如果用常规解法,有时运算量大,过程烦琐,若没有扎实的基础很难做出。若能用性质或一些常用的结论去处理,不仅运算简便得多,问题也很容易得到解决,尤其对一些选择题、填空题,会收到事半功倍的效果。下面就一些性质或结论在解题中的应用进行分享。
一、函数中的应用
例1 已知函数f(x)=l n(1+|x|)—,则使得f(x)>f(2x—1)成立的x的取值范围是( )。
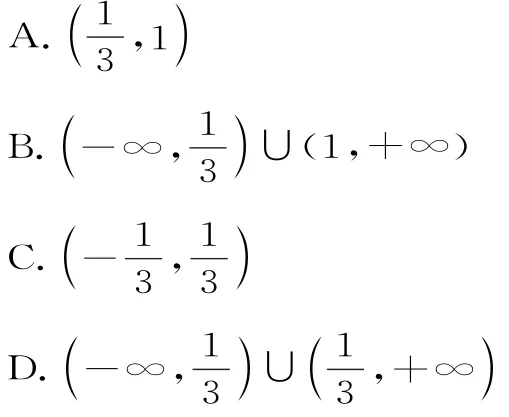
解析:由f(x)=l n(1+|x|)—,可知f(x)是偶函数,且在[0,+∞)上是增函数,所以f(x)>f(2x—1)⇒f(|x|)>故选A。
本题是考查函数性质的综合题,是高考重点考查内容之一。若此题用其他方法去解,不仅运算量大,而且运算困难。若用偶函数的性质去解,则运算过程简单,会有事半功倍的效果。
二、立体几何中的应用
在立体几何斜二测画法中,原图形的面积与其直观图的面积之间的关系有以下性质
例2 如果等边三角形的边长为1,那么它的平面直观图的面积为( )。
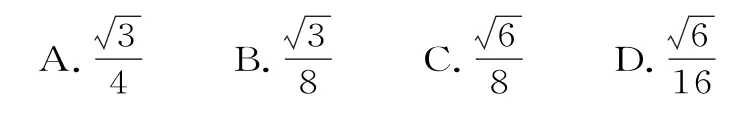
此题若利用斜二测画法画出直观图,再求面积,则比较麻烦,而用上述性质,则使解题变得容易。
三、三角函数中的应用
在三角函数中,函数y=Asin(ω x+φ)(A>0,ω>0)的性质:
(1)函数y=Asin(ω x+φ)为奇函数⇒φ=kπ(k∈Z);函数y=Asin(ω x+φ)(φ≠0)为偶函数⇒φ=kπ+(k∈Z);
(2)函数y=Ac o s(ω x+φ)(φ≠0)为奇函数⇒φ=kπ+(k∈Z);函数y=Ac o s(ω x+φ)为偶函数⇒φ=kπ(k∈Z)。
例3 函数y=sin(2x+φ)的图像沿x轴向左平移个单位后,得到一个偶函数的图像,则φ的一个可能取值为( )。
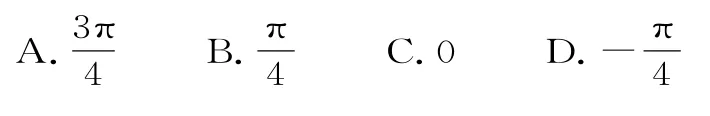
解析:将已知函数y=sin(2x+φ)的图像沿x轴向左平移个单位后,得到函数y的图像,由已知条件知它为偶函数,则+kπ,k∈Z,即φ=+kπ,k∈Z。故选B。
此题考查三角函数的图像及其变化,若由偶函数f(x)=f(—x)代入去做,则会比较麻烦。
四、平面向量中的应用
在△A B C中,角A,B,C所对应的边长分别为a,b,c,有以下重要结论:
例4 已知O,N,P三点在△A B C所在 的 平 面 内 ,则点O,N,P依次是△A B C的( )。
A.重心,外心,垂心
B.重心,外心,内心
C.外心,重心,垂心
D.外心,重心,内心
解析:由上面的结论知答案为C。
熟记一些重要性质和结论,并能灵活运用,对培养同学们的数学思维能力、分析问题和解决问题的能力,以及提高同学们的数学素养具有积极作用。
五、解析几何中的应用
1.双曲线中的应用。
例5(1)与双曲线=1有共同的渐近线,且过点(—3,2)的双曲线的标准方程是( )。
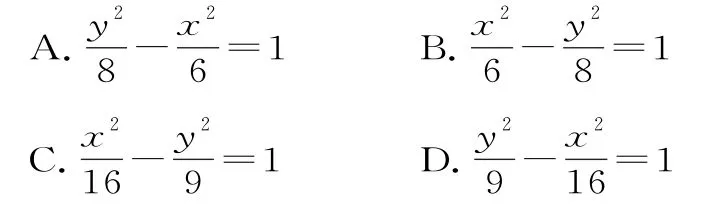
(2)双曲线的一条渐近线方程为2x—3y=0,且过点(—,—2)的双曲线方程是____。
解析:(1)设所求双曲线方程为=λ(λ≠0),又双曲线过点(—3,2),所以=λ(λ≠0),解得λ=—2,故所求双曲线方程是
(2)设所求双曲线方程为4x2—9y2=λ(λ≠0),又双曲线过点(—,—2),所以4·(—)2—9·(—2)2=λ(λ≠0),解得λ=—1 2,故所求双曲线方程是4x2—9y2=—1 2,即
本题是双曲线标准方程和性质的题型,如果用分类代入去做,则不仅运算烦琐,浪费时间,而且对解方程的要求比较高。
2.抛物线中的应用。
在抛物线中,过抛物线y2=2p x(p>0)的焦点F的直线交抛物线于A,B两点,则对于其他几种抛物线仍然适用。
例6过抛物线y=4a x2(a>0)的焦点F作一直线交抛物线于A,B两点,若|A F|,|B F|的长分别是m,n,则( )。
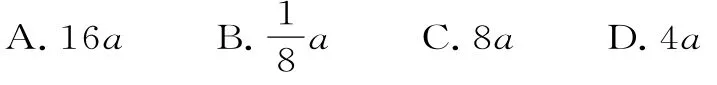
解析:由已知(a>0),则2p=,所以故选A。
类似本文所给出的性质和结论在高中数学中还有很多,需要我们在学习过程中及时加以总结,并牢牢记住它们。同学们在学习过程中应有意识地对这类题进行训练,这样有助于提升同学们的数学思维能力,提高数学素养,从而激发同学们的求知欲,增强解题成就感,树立学习数学的信心。
