基于随机化分析的等价空间故障检测方法
2019-04-08,,
,,
(山东科技大学 电气与自动化工程学院,山东 青岛 266590)
近三十年,针对故障检测与诊断技术研究的蓬勃发展,大量理论创新成果不断被提出,研究框架也逐步完善[1-2]。故障检测与诊断技术一般可为两大类,基于系统模型的方法和不依赖系统模型的方法。基于模型的故障检测与诊断技术通常包括残差生成和残差评价两部分,其中经典方法有基于观测器的方法[3-7]、基于等价空间的方法[8-11]和基于参数估计的方法。
等价空间方法利用有限时间窗内系统输入与输出(或部分输出)之间的冗余关系构造残差,可实现残差与系统初始状态解耦。众多学者对等价空间方法进行了深入的研究,文献[12]将小波变换与等价空间方法结合,利用小波变换的时频局部化特性和快速算法,有效降低等价阶数,实现对较宽频率范围内故障的检测。文献[13]针对线性离散时变系统计算量大的问题,将残差评价函数的计算问题转化为求解Krein空间投影问题,提出一种递推的故障检测快速算法,显著降低运算量,提高了故障检测系统实时性。文献[14]应用KL散度联合故障距离函数和故障方向函数设计故障可诊断性指标,研究了线性离散系统的可诊断性问题。
基于易于应用方面的考虑,设定一个保守型阈值可以使误报率为零,从而避免错误报警的干扰。但发生微小故障(如在故障发生的初期)时,阈值过强的保守性会使故障检测率大大下降。文献[15]提出基于概率不等式方法的随机化算法,能够应用蒙特卡罗模拟对性能指标进行有效估计,运用此方法可以将检测系统性能评估问题转化为对一系列随机实验的随机化分析问题。文献[16]分析了应用主元分析窗口平滑和指数加权方法对检测微小故障的检测能力的提升效果,为阈值选取和提升故障检测率提供了思路。
本研究以噪声和扰动统计特性未知,但有限时间l2范数有界的系统为研究对象,研究随机化分析辅助的等价空间故障检测方法。为权衡误报率和故障检测率两项性能指标,得到较高检测效率,基于随机化分析对误报率和漏报率估计结果,给出了检测阈值的选取方法。最后,以无人机纵向控制系统故障检测平台为例,验证提出方法的有效性。
1 问题描述
考虑如下的线性离散系统
(1)
式中:x(k)∈Rn,u(k)∈Rp,y(k)∈Rq分别为状态向量、输入向量以及输出向量;d(k)∈Rl代表未知干扰和其他故障;f(k)∈Rm表示待检测的故障向量;A,B,C,D,Ed,Ef,Fd,Ff为相应维数的已知矩阵。
令
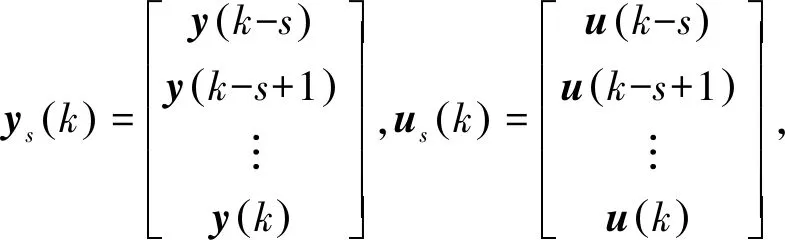
其中s为等价阶数,可得
ys(k)=Hosx(k-s)+Husus(k)+Hdsds(k)+Hfsfs(k)。
其中
将Hfs中的{Ef,Ff}分别替换为{Ed,Fd}和{B,D}可得Hds和Hus。构造如下的残差生成器
r(k)=Vs[ys(k)-Husus(k)]=Vs[Hdsds(k)+Hfsfs(k)]。
(2)
其中:r(k)为残差向量;Vs∈Rγ×s·m为待设计的等价矩阵,且满足VsHos=0;γ为等价空间Ρs(Hos的左零空间)的维数。
残差对未知扰动的鲁棒性和对故障的敏感度分别定义为:

(3)
则残差产生器的设计问题可以转化为如下的最小化问题:

(4)
由式(4)求得残差评价量以后,依据未知干扰的类型(统计特性已知,如白噪声;或有限时间内范数有界),选择适当的阈值Jth,并基于如下逻辑判断故障的发生:

如果未知扰动在有限时间内能量有上确界,则利用未知扰动的上确界可以确定故障检测系统的零误报率检测阈值:
由于被检测对象所处环境和状态的不确定性,很难获得准确的未知扰动的上确界。即使已知未知扰动的上确界,设置Jth,FAR=0为检测阈值,不可避免会带来一定的故障漏报率。检测系统的漏报率和故障的大小有很直接的关系,微小故障和早期故障的漏报率对阈值的选取比较敏感。当系统发生微小故障时,适当降低检测阈值保守性会改善系统的检测性能。设定合适阈值,使检测系统的误报率和漏报率性得到最优权衡是一个设计难点。
2 故障检测系统设计
2.1 残差生成器设计
在残差生成器设计时,设计残差向量r(k)=Vs[Hdsds(k)+Hfsfs(k)]且将等价矩阵Vs的求解过程转化为性能指标的最小化问题:

(5)
式中Ws为待设计等价矩阵,满足Vs=WsNsbasis.性能指标也相应改写为:
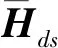
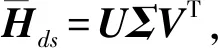
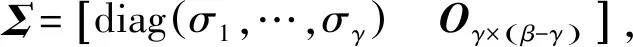
S=diag(σ1,…,σγ)。

根据2范数的定义:
由矩阵范数的相容条件
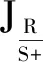

得到如下的引理。

2.2 随机化算法与阈值选取
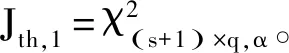
若扰动d(k)不满足白噪声,但在有限时间内l2范数存在上界,那么残差评价量Js(k)必然存在上界Js(k)≤δ2。假设残差评价量Js(k)的分布函数为FJs(k)(·),显然FJs(k)(δ2)=1。如何设计采样复杂度M对δ2进行估计,不仅影响估计结果的可信度,并且很大程度影响算法的工程可实现性。文献[15]给出了一种估计分布极值取样复杂度的计算方法。
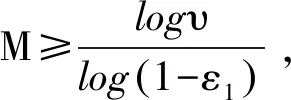

设定检测阈值为Jth,2=δ2,可以有效避免误报的发生,但当有微小故障发生时,故障的漏报率会显著升高。显然,此时选择Jth,2=δ2为检测阈值保守性是过强的。适当降低阈值的保守性会改善故障漏报率高的问题,但是降低过多同样会引起误报率指标的上行。如果能够获取当前设定阈值的误报率漏报率的准确信息,将对阈值的最优选取提供理论参考。文献[15]给出了一种估计系统性能指标的随机化算法。此方法可以应用于对误报率进行估计。

引理3[15](Chernoff界引理): 给定任意ε∈(0,1),δ∈(0,1),如果

证明:对于随机变量序列x1,…,xN,由于
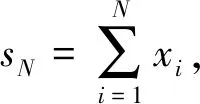

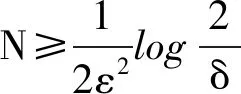
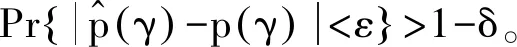
假定未知扰动d(k)是各采样点相互独立的随机过程向量,根据引理3的Chernoff界中采样复杂度的计算方法,通过如下的统计试验估计无故障时相应检测阈值的误报率。
步骤1在无故障时对残差评价进行M次独立采样Js(k),k=1,2,…,M。
步骤2选定待估计的系统阈值Jth,2。
步骤3做如下的次数统计:
步骤4计算系统阈值Jth,2的误报率为:
利用Chernoff界计算不等式可以得到以下结论:


3 仿真实验
为验证以上方法的有效性,在MATLAB仿真环境下,以某固定翼无人机纵向飞行控制系统故障检测仿真平台为例进行验证。无人机系统线性化模型[12-17]如下:

(6)
式中:
Ac=[

-0.0127.5230-9.80-0.0009-1.86561000.0035-10.97-0.33600001000-124.920124.920
Bc=[

-0.020 10.065-0.002 30-0.212 8-0.001 90000
考虑系统量测噪声为互不相关的均值为0,方差为0.1的白噪声。取采样周期为0.01 s,将线性化后的无人机纵向系统模型离散化,得到无人机纵向离散化系统模型为
(7)
1)无人机执行器故障
将无人机执行器故障描述为如下的加性故障:
uf(k)=u(k)+f(k),kstart≤k≤kend。
式中:kstart为故障开始时间,kend为故障消失时间,u(k)为执行器输入指令,f(k)为执行器故障信号,uf(k)为执行器的实际输出。则无人机纵向系统故障模型可以表示如下:
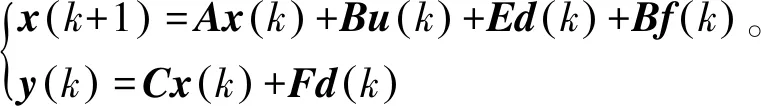
(8)
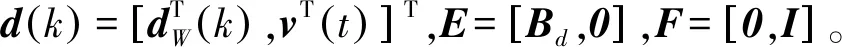
设定仿真时间为180 s,步长为0.01 s,利用上文提出的方法设计故障检测系统,其中,等价阶数设置为30。前100 s为无故障正常飞行状态,在110 s和140 s,分别注入升降舵部分失效故障,分别为失效10%和失效8%。前100 s无故障飞行时,对残差评价量JS(k)构造如下的统计量:
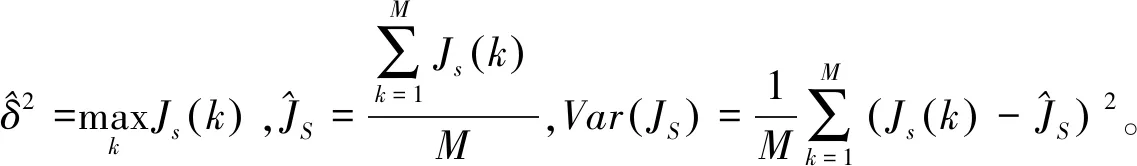
利用以上统计量构建如下的三个检测阈值:
以Jth,1,Jth,2,Jth,3为检测阈值,设计故障检测系统,检测结果如图1所示。

图1 升降舵部分失效故障检测波形Fig.1 Waveforms of elevator partial failure fault detection


表1 执行器故障系统阈值及其误报率漏报率Tab.1 Threshold value of actuator fault dection system and its false alarm rate and missing alarm rate

2)无人机传感器故障
将无人机传感器故障描述为如下的加性故障:
yf(k)=y(k)+f(k),kstart≤k≤kend。
式中:kstart为故障开始时间,kend为故障消失时间,y(k)为输出变量真实值,f(k)为传感器故障信号,yf(k)为传感器的实际输出。则无人机纵向系统故障模型可以表示如下:
(9)
式中,Ff为适当维数的单位阵。
使用上文实验中故障检测系统对飞行器传感器故障进行检测。前100 s为无故障正常飞行状态,在110 s和140 s,分别注入飞行高度传感器增益故障,增益分别为2.0和1.8。检测波形和实验结果分别如图2和表2所示。
对于无人机其他类型故障,如传感器以及执行器的偏差故障和卡死故障,均可以转化为加性故障信号,本研究提出的方法同样适用于以上类型的故障检测。
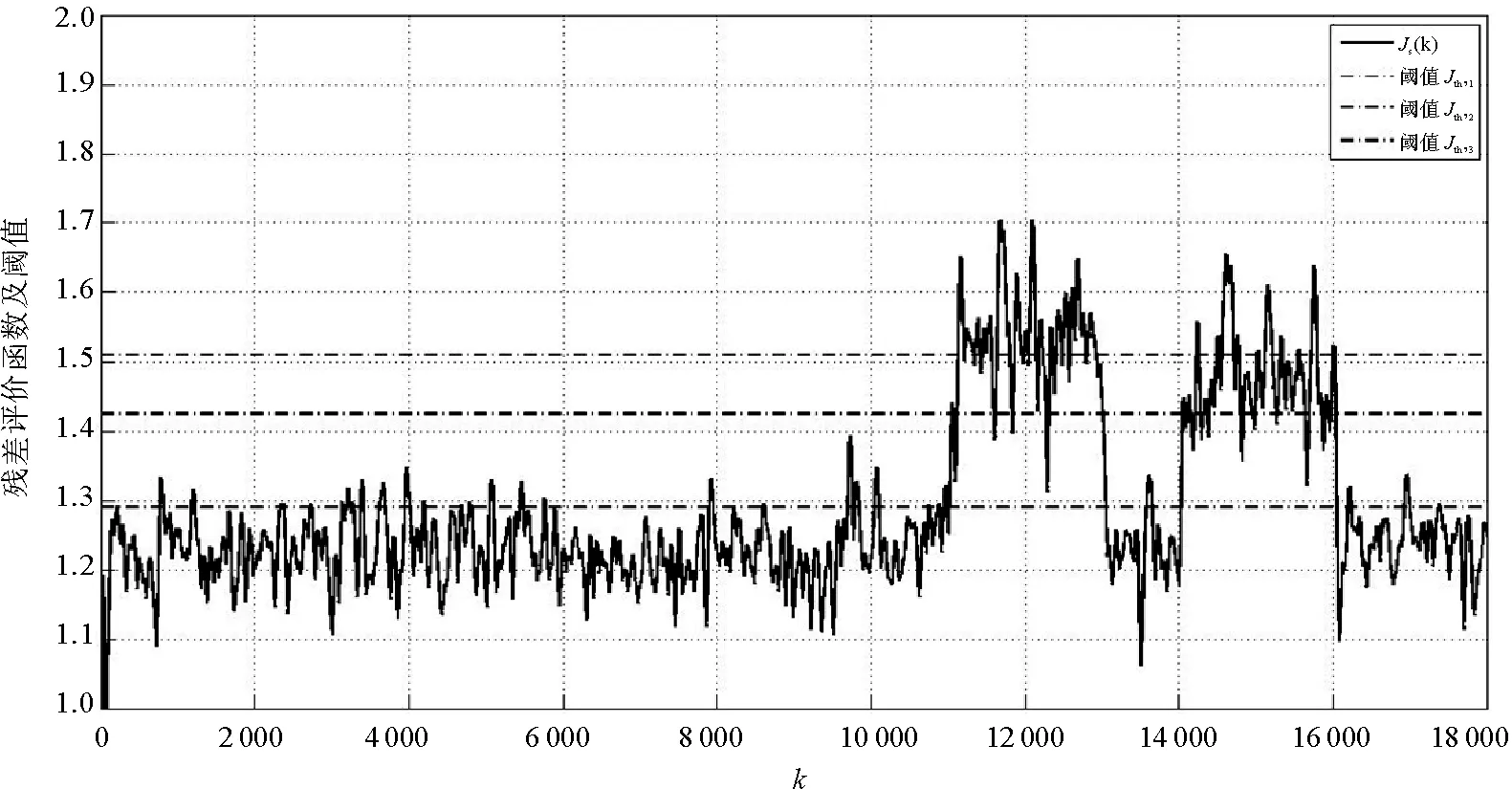
图2 飞行高度传感器增益故障检测波形Fig.2 Waveforms of flight altitude sensor gain fault detection

系统阈值Jth,1=1.510 7Jth,2=1.288 7Jth,3=1.424 9误报率00.153 00.002 72.0增益故障漏报率0.442 00.030 00.167 51.8增益故障漏报率0.681 50.019 50.340 5
4 结论
本研究提出一种随机化分析辅助的等价空间故障检测方法的设计问题。应用概率不等式的方法,通过蒙特卡洛模拟估计故障检测性能指标、误报率和漏报率,并依据估计结果设定检测阈值的方法。在保证误报率指标较低的条件下,应用所提方法可以提高故障检测系统对微小故障的故障检测率。最后利用无人机纵向控制系统故障检测模型对所提方法进行了仿真验证。
