一类时滞SIR传染病模型行波解的不存在性
2019-04-08晁玉园孙福芹
晁玉园,孙福芹
(天津职业技术师范大学理学院,天津 300222)
随着现代卫生设施以及医疗水平的提高,对于传染病规律和防止策略的研究日益重要。在现实生活中,某些疾病有一定时间的潜伏期,因此对于具有潜伏期流行性疾病的研究,在生活中也有重要的应用[1-2]。自从Kermack等[3]建立传染病数学模型以来,传染病模型以及其衍生模型如SIR传染病模型,被频繁用来研究各类流行疾病。探究疾病原因,找到最优解决方案已经成为十分重要的课题。其中,对传染病模型的行波解存在性和动力学行为的数学分析及其数值模拟已经成为生物数学研究的一个热门方向。如2010年Wang等[4]考虑了Kermack-McKendrick扩散模型的行波解的存在性问题;2017年Cheng等[5]进一步研究了Kermack-McKendrick非局部扩散模型的行波解存在性问题;2014年和2015年,文献[6-7]分别研究了2类非局部SIR传染病模型的行波解的存在性问题。研究行波解具有非常重要的实际意义,行波解的存在意味着传染病以常数速度在空间中传播。由于行波解即使在微小扰动下,其性质也可能发生本质改变,因此对行波解的定性性质诸如行波解的渐近行为、稳定性及唯一性等问题的研究也十分必要。本文将在文献[6]研究的基础上,对时滞模型在满足一定条件时,行波解的不存在性进行研究。
1 模型介绍和假设
文献[6]研究了如下非线性非局部扩散SIR传染病模型的行波解问题:


易知模型的基本再生数为R0:=β/γ,研究基本再生数与波速在满足哪些条件时,模型不存在非负非平凡行波解。由于模型(1)的前2个方程可以构成独立的子系统,因此主要考虑前2个方程构成的子系统的行波解问题。若模型(1)具有行波解,令ξ=x+ct,其中c>0为波速,则模型(1)的前2个方程可化为如下形式:

由生物学意义,设问题(2)满足如下边界条件:

式中:S0为正常数,表示未感染之前易感染者的数量。
假设初始平衡状态为(S0,0)。为研究式(2)和式(3)的行波解,对函数J(y)作以下假设:
2 主要结论和证明
在给出主要结论之前,将给出问题(2)特征方程及性质。将模型(2)的第2个方程在平衡点(S0,0)处线性化之后,可以得到:

令I(ξ)=eλξ并代入式(4),可得特征方程:
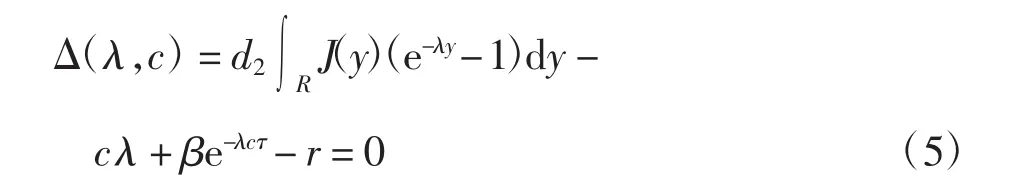
以下是式(5)的一个性质。

(1)如果 0< c< c*,那么 Δ(λ,c)> 0 对于所有λ∈(0,+∞)都成立;

证明因为 R0= β/γ > 1,所以 Δ(0,c)= β-γ>0。对于任意 c>0,有 Δ(+∞,c)=+∞。计算可得:

综上,可完成引理证明。
讨论 R0>1,0< c< c*以及 R0≤1,c> 0时模型(2)不存在满足条件(3)的非负非平凡行波解,所用到的方法和技巧为双边Laplace变换[8-9]和一系列积分估计。
定理1假设R0=β/γ>1。对于任何满足0<c<c*的波速c,系统(2)不存在满足条件(3)的非负非平凡行波解。
证明利用反证法。假设系统(2)存在满足条件(3)的非负非平凡行波解(S(ξ),I(ξ))。根据式(3),知当ξ→-∞ 时,


利用系统(2)的第2个方程,有

对上式从-∞→ξ(ξ<ξ*)积分后化简可得:

另外

由此可得 J*Q(s)-Q(s)和 Q(s-cτ)-Q(s)在(-∞,ξ)是可积的。将式(6)从-∞→ξ(ξ< ξ*)积分化简后可得:

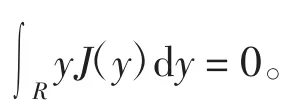

因为Q(ξ)关于ξ是一个非减函数,所以存在s*并且s*+cτ>0使得:

易知存在足够大常数 s0> -cτ和 v∈(0,1),使得Q(ξ-(s0+cτ))≤vQ(ξ),∀ξ< ξ*。
定义

则



所以对于上式由-∞→ξ积分,可得cI(ξ)≤d2(J*Q(ξ)-Q(ξ))+ βQ(ξ-cτ)- γQ(ξ),其中



即得:



其中易知
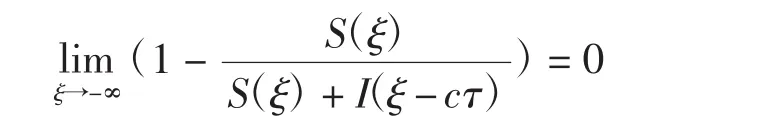
选取0<w<u0,根据文献[10]中的定理3.1的证明,可以得到

式中:K为常量并且依赖于w。
运用双边Laplace变换性质[9],式(7)可以改写为:

定理2假设R0=β/γ≤1。对于任何满足c>0的波速c,系统(2)不存在满足条件(3)的非负非平凡行波解。
证明利用反证法。假设系统(2)存在满足条件(3)的非负非平凡行波解(S(ξ),I(ξ))。
若R0=β/γ<1,对于系统(2)第2个方程两边在R上进行积分,可得:


根据 R0=β/γ < 1,式(8)可得:

此为矛盾。
若 R0= β/γ =1,对于系统(2)的第 2个方程可以得到:

对于上式在区间R上积分,运用Fubini定理以及I(±∞)=0,可得:
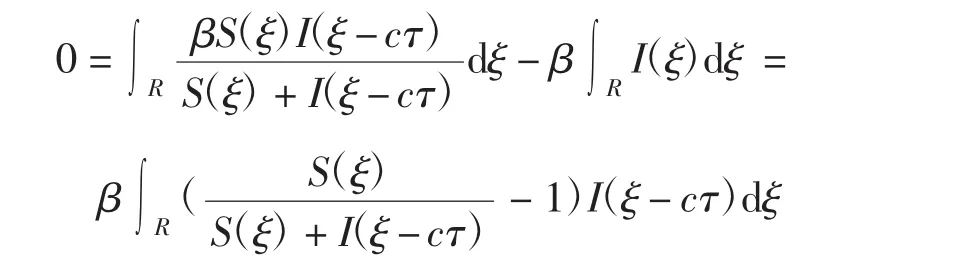
由于

且I(ξ)为非负函数,可以得到:

容易得知对于suppI内部是非空的,所以对于ξ∈suppI有:

这也是一个矛盾,定理证毕。
3 结语
本文主要研究SIR模型在有时滞现象时行波解的存在情况。分别证明当基本再生数与波速满足条件R0> 1,0< c< c*以及R0≤1,c> 0时,SIR模型不存在非负的非平凡的行波解。对行波解的存在性以及存在性条件,限于篇幅本文没有涉及。关于流行病模型的研究,还会涉及其他一些因素以及相关的变量,仍需要进一步研究。
