基于正弦饱和函数的永磁同步电机滑模观测器研究

陈俊杰,迟长春

(上海电机学院 电气学院,上海 201306)

0 引言

目前永磁同步电机运用广泛，对于永磁同步电机速度和转子位置的获取非常关键[1]。传统的机械传感器成本高,容易受到环境的影响而且增大了电机的体积，对此专家、学者对无传感器技术做了深入的研究，其中主流的方法有：模型参考自适应法、扩展卡尔曼滤波器法、人工智能方法等等[3-7]。对于滑模观测器的优化：文献[8]以转速误差为滑模面建立滑模观测器代替传统的PI控制器，虽然双滑模控制可以降低转速的超调量，但系统的抖振不容易避免；文献[9]利用sigmoid代替开关函数，用锁相环估计电机的速度和位置，但是对估计反电势过滤的低通滤波器不具有自适应性，系统速度发生变化时的滤波效果不佳，往往会加大误差；文献[10]针对滑模变结构存在的抖振问题提出用饱和函数的方法，提高转速精确度，但是饱和函数的效果往往不如非线性的函数来得好；文献[11]设计了一种新型二阶滑模观测器，将混合非奇异滑模终端滑面应用到传统的线性滑模面上，降低了相位滞后和抖振问题；但高阶滑模设计优化复杂，对硬件要求相对较高；文献[12]针对传统滑模控制的抖振和相位延迟问题，提出用自适应模糊滑模观测器来实现，但模糊规则在实际中需要经验，难以掌握。

本文在针对一阶传统滑模观测器出现的抖振问题进行改进：在电流环和速度环用正弦型饱和函数代替开关函数；用变截止频率低通滤波器代替传统低通滤波器，这样可以缩短相位延迟，防止因截止频率选取不当导致的转速偏差；最后使用卡尔曼滤波器过滤估算反电势的高频信号得到更加连续平滑的反电势，进一步提高估计的准确性。

1 传统滑模控制原理

滑模控制的输入是永磁同步电机的电流和电压，输出是电机的转速和转角位置。为了建立滑模观测器，建立电机在α和β轴的数学模型[13-14]：

(1)

(2)

包含电流差的开关函数具有反电势信息，故eα和eβ可作为反电势的估算量zα和zβ，式子可表示为：

(3)

经过开关函数得到的反电势信息中含有大量的高频信号，经过低通滤波器过滤后的反电势公式如下：

(4)

其中,ωc是低通滤波截止频率。

估计电动势通过低通滤波器会带来相位延迟，可以用电机的估计转速和截止频率计算，公式如下：

(5)

其中,ωc是系统的截止频率。

补偿后的转子位置估计角度和转速的公式如下：

(6)

传统滑模控制的流程图如下：

图1 传统滑模算法的结构框图

2 改进的滑模观测器

2.1 基于正弦饱和函数型的抖振削弱

此外传统开关函数不具有连续性，会因为系统的惯性、测量的误差等原因导致在滑模面反复穿梭，形成锯齿状的运动轨迹。为了降低开关函数带来的抖振问题，给切换函数切换处增加一段缓冲，这里用正弦型饱和函数进行研究。

图2 正弦性饱和函数原理图

饱和函数表达式为：

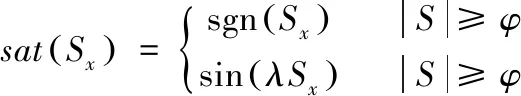
(7)

其中，λ=π/2φ。

由式(7)可知：正弦型饱和函数sat是一种非线性函数。为了保证滑模切换的速度，边界层的厚度可以自动调节，随着电机转速做出自适应变化，降低抖振，提高系统稳定性和观测器的效果。

近年来，我国公路交通事业发展迅猛，公路隧道竖井的数量随之增加，其中竖井衬砌的安全性评价显得尤为重要。本文以荣乌高速营尔岭隧道排烟竖井为例，结合其设计支护参数，采用三维岩土分析和隧道有限元软件MIDAS/GTS NX对周边环境和其施工过程进行模拟计算，依据模拟结果对其竖井施工方法和衬砌支护的安全性进行评价。

2.2 变截止频率低通滤波器和卡尔曼滤波器组合

由于电机变速的过程中，传统的滑模截止频率是有个定值，很难真正对各个速度段做有效的滤波，这里用可变频率截止滤波器来代替传统滤波器，可变频率截止滤波器的表达式为：

(8)

其中，kf是正数，ke的数值较小，此时截止频率与电机的转速有关。

经过低通滤波器的反电势信息量依然含有测试噪声，此时用卡尔曼滤波器进行二次滤波，滤去高频纹波得到连续光滑的估算反电势，可以有效减小抖振使系统具有更好的工作性能。

电机的反电势可以表示为：

(9)

对电机反电势公式求导可以得到：

(10)

在电机的无传感器滑模控制中，系统的采样频率小于电机转速的变化量。这里可以将电机转速的导数看成是0，则公式可表示为：

(11)

(12)

卡尔曼滤波器如下：

(13)

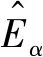
验证稳定性，用李雅普诺夫公式判断可得：

(14)

对上述公式求导可得：

(15)

将式(13)带入式(15)可得：

(16)

可以证明加入卡尔曼滤波器后的系统是稳定的。

3 仿真结果及其分析

永磁同步电机在实际的运行过程中，有匀速、变速和负载扰动三种情况。本实验利用Matlab软件进行仿真，电机极对数P是4,定子电感Ls=8.5mH，定子电阻R=2.875Ω，磁链Φf=0.175Wb，转动惯量J=0.001kg·m2，阻尼系数B=0，直流侧电压U=311V，开关频率f=10kHz。分别读取电机的转速值、转速差来看滑模观测器的实际性能。本文所写基于正弦饱和函数的滑模控制永磁同步电机模型，如图3所示。

图3 基于改进滑模永磁同步电机控制结构框图

本次仿真实验主要研究永磁同步电机在变速和变力的实际条件下，估算转速的准确性，实验如下：

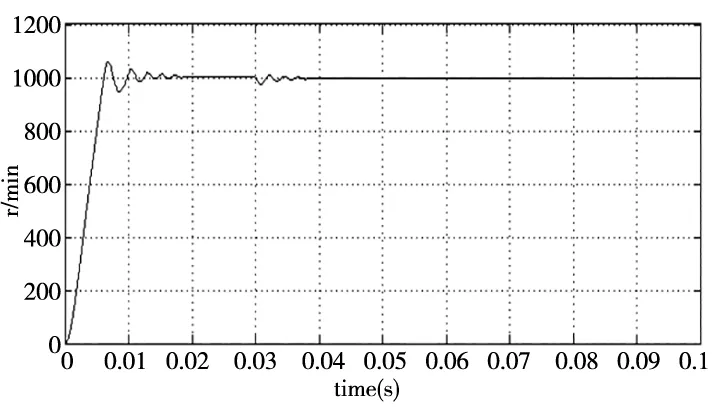
(1)研究永磁同步电机在均速状态下的转速估算情况，对比传统滑模观测器和改进型滑模观测器，本实验总时间0.1s，给定转速1000r/min，空载启动，其中纵坐标代表转速，横坐标代表时间，结果如图4所示。

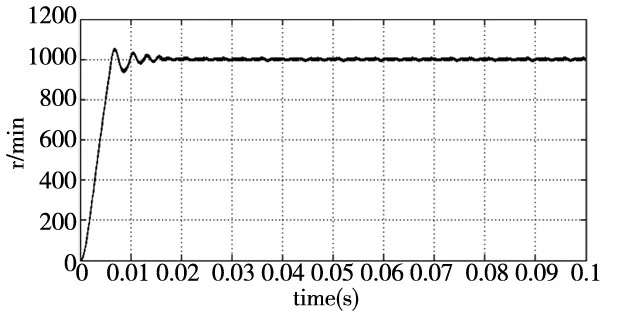
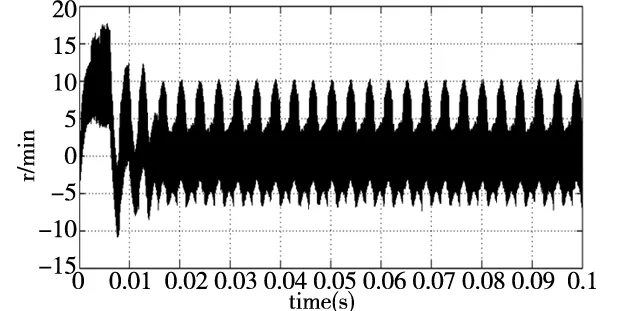
(a) 传统滑模控制下的转速和转速差

(b) 基于改进后的滑模控制下的转速和转速差图4 均速下滑模观测器的转速和转速差

当给定转速是1000r/min时，根据图4a可知：传统滑模的最大转速差达到16r/min，超调量是1.6%，进入稳定后转速差在11r/min；图4b的改进后的滑模器启动最大转速差仅为10r/min，超调量是百分之1%，进入稳定后转速差在0.4r/min，估计转速基本与实际转速相一致。

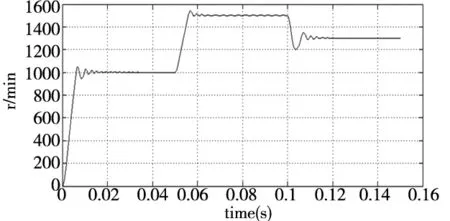
(2)研究永磁同步电机在变速情况下转速的估计情况，设置实验总时间为0.15s，先是给定转速是1000r/min持续0.05s；再给定转速是1500r/min持续0.05s；最后在0.1时，给定转速是1300r/min持续0.05s，其中纵坐标代表转速，横坐标代表时间，结果如图5所示。

(a) 传统滑模控制下的转速和转速差

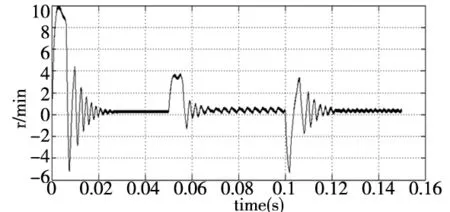
(b) 改进后的滑模控制下的转速和转速差图5 变速下滑模观测器的转速和转速差

图5b在图5a的基础上加了变截止低通滤波器代替传统低通滤波器；用正弦饱和函数代替符号开关函数。根据图5a可知：系统在1000r/min,1500r/min和1300r/min的情况下都可以保持稳定；从图5b可知在1000r/min时，传统滑模观测器的转差达到11r/min；在1500r/min和1300r/min时，转差分别是8r/min和7r/min而改进型的滑模观测器转差分别是0.3r/min，0.55r/min和0.45r/min，利用改进滑模观测器效果明显。

(3)研究永磁同步电机在运行时候，外界扰动对系统运行稳定性和滑模观测器输出转速的影响。分别在电机启动阶段，稳定运行阶段加上扰动，本实验总时间为0.1s，电机的参考转速是1000r/m，在0.005s，减载-1N·m；在0.03s加上一个5N·m的负载，研究系统的稳定性和估算转速误差，其中纵坐标代表转速，横坐标代表时间，结果如图6所示。

(a) 负荷变化后改进滑模模型转速输出曲线

(b) 负荷变化后改进滑模控制的电机转差分析图6 负荷变化后改进滑模的转速和转差分析

本实验在电机启动阶段(0.005s)和正常运行阶段(0.03s)分别施加-1N·m和5N·m的负荷，控制系统在0.03s时，转速出现振荡，转速差增大到2.3r/m。在0.04s时电机再次稳定运行。对比扰动前和扰动后可知，电机转差有一定幅度的增加，说明扰动对系统有一定程度的影响，由图6b的转差图可知，在稳定后，转差一般保持0.3r/min和0.45r/min，数值很小。这两处针对电机启动、稳定运行扰动实验说明了使用正弦饱和函数滑模系统的稳定性和估算转速良好的性能。

4 结论

针对传统滑模观测器存在的抖振问题，本文将传统滑模函数中的符号开关函数用正弦性饱和函数代替进行研究，实际情况表明电机运行更加平稳同时电机的实际转速与估算转速的误差减小，系统的鲁棒性提高。其次加入变截止低通滤波器和卡尔曼滤波器也有利于减小误差，增加稳定性。