失压电量追补自动计算方法的误差研究

纪 峰 ，程含渺 ，许 蔺，夏国芳

(1.国网江苏省电力有限公司电力科学研究院,江苏 南京 210019；2.国家电网公司电能计量重点试验室， 江苏 南京 210019；3.南京聚能农电有限公司,江苏 南京 210039)

0 引言

在现场运行过程中，失压是电能计量装置经常发生的故障之一。失压故障往往会造成少计电量，需要事后追补。目前，一般采用人工分析计算的方法。该方法存在计算方法不统一的问题，需要假设三相负荷对称，费时费力，不符合用电智能化要求[1-2]。随着智能电网的发展，电网运行的自动化水平越来越高，智能电能表的应用也已经普及。寻求采用新的自动化计算方法取代传统的人工计算[3-4]。在此背景下，文献[5]提出了一种基于假设三相电压平衡条件下利用未失压相电压追补失压故障下的电能的方法(以下简称“相电压替代电量追补法”)。该方法无需假定三相负荷电流平衡，在一定程度上提高了电量追补准确性。目前，该方法已经在广东地区应用，但尚未大范围推广。原因之一是该方法因需假设三相电压平衡而存在误差，而且误差水平尚无定量研究。

本文在文献[5]的基础上，主要做了两方面工作。一是在理论上定量分析了这种电量追补方法的误差；二是结合实际运行工况，给出了该方法在实际应用时的误差。研究结果表明，该电量追补方法的误差在理论上可能较大，但应用于实际工况时误差不超过4%。这为该方法的推广应用提供了理论依据。

1 相电压替代电量追补法基本原理

以三相四线制为例，相电压替代电量追补法的基本原理是：将正常相的电压矢量旋转120°(或240°)，以替代失压相电压。

相电压替代法矢量图如图1所示。

图1 相电压替代法矢量图Fig.1 Vector diagram of phase voltage substitution method

图1中，假设A相失压，则将B相电压逆时针旋转120°，替代A相电压，以计算失压时间段内少计量的电能量。

2 相电压替代追补电量法的误差分析

由相电压替代追补电量法的原理可知，三相电压不平衡会产生电量计算误差。根据国家标准《电能质量 三相电压不平衡》规定，电力系统公共连接点正常电压不平衡度限值为2%，短时不超过4%[6]。

电子式电能表由电能累加单元完成计量功能，三相电压相互独立，相间基本无影响[7-9]。在规定的接线条件下，三相电压不平衡对电子式电能表产生的附加误差可以忽略。因此，相电压替代电量追补方法的误差，只与相电压替代误差有关，包括电压幅值差和相位差。以下分析均假设A相失压，用B相电压替代A相电压。

2.1 电压替代幅值误差

假设A、B两相电压夹角为120°+φAB，B、C两相夹角为120°+φBC，规定逆时针方向为正。采用对称分量法将三相电压分解为三相对称电压，如式(1)所示：

(1)

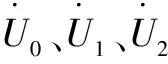
(2)

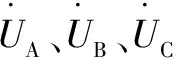
(3)

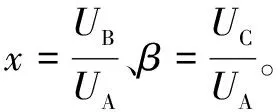
(1-ε)2x2+[2cos(120+φAB)+2βcos(240+φAB-φBC)-2ε2cosφAB-2ε2βcos(φAB-φBC)]x+1+β2-ε2-

ε2β2+2βcos(-120+φBC)-2βε2cosφBC=0

(4)

分析式(4)可知，其为关于x的一元二次方程，所以方程必然有两个由φAB、φBC和β构成的解空间。

为了评估使用相电压替代电量追补方法追补电量的计算误差，采用遍历的数值仿真方法。边界设置如下：①电压不平衡度设置为ε=0.02;②φAB和ΦBC取值区间设置为[-8.6°,8.6°]，计算步进取0.06°；③β取值区间设置为[0.5,1.5]，计算步进取0.01。根据x的实际物理意义，解空间内的正实数为有效解，负实数和虚数均为无效解，得到x的两个有效3维解空间。3个维度分别是φAB、φBC和β。

分别从两个解空间中找出使得x取极大值或者极小值的解，即UA和UB的差值达到最大的点。

①在第一个解空间，当x为最小值时，有：

(5)

当x为最大值时，有：

(6)

②在第二个解空间中，当x为最小值时，有：

(7)

当x为最大值时，有：

(8)

由以上分析可知，相电压替代电量追补方法在实施过程中，在本文数值仿真设定的范围内，电压替代幅值误差最大约36%。

2.2 电压替代相位误差

由于A、B两相电压实际夹角为120°+φAB，所以将B相电压逆时针旋转120°，以替代A相电压。由此产生的替代相位误差为：

Δφ=(120°+φAB)-120°=φAB

(9)

在本文数值仿真设定的范围内，电压替代相位误差绝对值最大，为8.6°。

2.3 追补电能误差

三相功率计算公式为：

P′=UAIAcosφA+UBIBcosφB+UCICcosφC

(10)

式中:φA、φB、φC分别是三相负荷功率因数角。采用B相电压替代A相之后，则式(10)变为：

(11)

(12)

(13)

当UB和IB的夹角为0°，即B相负荷的功率因数为1时，计算可得电量追补误差为24.6%。这说明，采用相电压替代电量追补法，失压电量追补误差在理论上非常大。

3 电压不平衡度的进一步讨论

第2节的计算结果中出现了一种现象，即电压幅值和相位不平衡度非常大，但电压不平衡度仍然是2%。为了验证这种现象，采用另外两种IEC定义的电压不平衡度进行验算。两种精确的IEC定义为[10]：①负序电压复数与正序电压复数的比值；②三相三线系统的线电压计算。将第1解空间最小值点的结果代入上述两种计算方法中进行验算。

3.1 第1种IEC精确定义

使用负序电压复数与正序电压复数的比值，其计算公式为：

(14)

式中:V1为正序电压相量；V2为负序电压相量。

以A相电压为参考，三相电压为：

(15)

将式(2)和式(15)代入式(14)，可得：

ε1=0.019 9∠43.42°

(16)

3.2 第2种IEC精确定义

使用三相三线系统的线电压计算方法，其计算公式为：

(17)

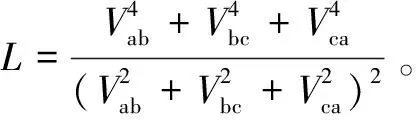
假设A相电压为220 V，相角为0°。

以A相电压为参考，线电压为：

(18)

将式(18)代入式(17)中，可得：

ε2=0.019 9

(19)

以上结果表明，使用不同的不平衡度计算方法，第一解空间中的x最小值点处的电压均满足不平衡度为2%。

4 应用于实际工况的误差分析

仿真结果三相四线制如表1所示。

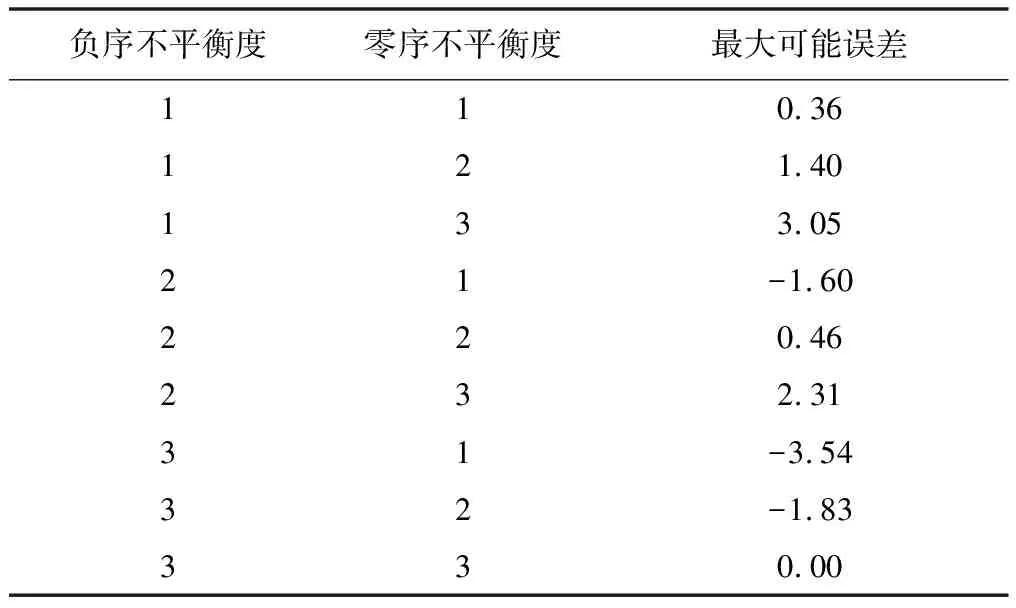
表1 仿真结果(三相四线制)Tab.1 Simalation results %

值得指出的是，文献[11]提供了一种更为直观的图解法，是本文维解空间的一种三维表示方法，可以快速确定电压替代误差。

5 结束语

本文对相电压替代电量追补法在线计算失压追补电量的误差进行了定量研究。研究结果表明：该方法在理论上可能引起的较大误差。其原因是误差受零序电压不平衡度影响显著，而国家标准暂时对零序电压不平衡度无明确规定。实际使用时，由于零序电压会控制在一定水平，使得该方法误差较小，对于三相三线制系统，当负序电压不平衡度小于2%时，电能追补误差小于3.55%；对于三相四线制系统，当负序电压不平衡度和零序电压不平衡度均小于2%时，电能追补误差小于2%。本文为相电压替代电量追补方法的实际推广应用提供了理论支撑。