微流体惯性过滤器的参数优化与数值模拟
2019-04-08牛风雷王仕集
张 薇,牛风雷,王仕集
(华北电力大学核科学与工程学院,北京 102206)
0 引言
为了防止反应堆严重事故后期出现放射性气溶胶外泄的问题,现役的大部分核电站已经增设了安全壳过滤排放系统[1],通过主动泄压的方式来保证安全壳的完整性。它的主要设备是过滤放射性气溶胶的过滤器。微流体惯性冲击式气溶胶过滤器[2]的实质是一个微流体惯性冲击器,该装置利用摄入粒子的惯性实现不同粒径的粒子与空气分离。由于尺寸微小、原理简单,该收集方式不需要更换过滤介质,就能过滤气溶胶粒子。同时,收集过程也不会对周围的压力环境产生影响,具有很高的应用价值[3]。
过滤效率和压降是评价过滤器性能的两个非常关键的参数,而影响这两个参数的主要因素有转折角、截面长度、管长和气流速度等[4]。目前,文献[4]已利用Fluent软件对微流体惯性过滤器内的流场和颗粒运动情况进行了数值模拟,虽然分析了不同因素对过滤器过滤效率和进出口压降的影响,但不能从客观上准确分析各个因素对过滤效率和压降的影响程度,同时不能科学设计出最佳的参数组合,所以有必要采取比较科学的优化设计方法,对微粒体惯性过滤器的工艺参数进行合理的设计。
本文以2 μm粒子为收集对象[5],设计冲击器。采用正交分析法,选取对过滤效率和压降有影响的4个主要因素(转折角、截面长度、管长和气流速度)进行优化研究,运用正交试验设计原理确定多种试验方案,进行相应的模拟计算。利用极差分析法和方差分析法对试验结果进行分析,从而得到各个因素的敏感性影响程度以及各因素的最佳水平。
1 正交试验设计
正交设计利用从试验的全部水平组合中,选择部分有代表性的水平组合进行试验,通过对这部分试验结果的分析了解全面试验的情况[6]。如前所述,影响过滤器过滤效率和压降的4个较敏感因素分别是转折角、截面长度、管长和气流速度。根据文献[4]中的计算结果,每个因素下选取4个水平进行试验,若进行全面试验需要做44=256次试验,但是采用正交表安排试验[7],只需做16次试验,就能够了解到4个因素对过滤效率和压降的影响程度。
试验因素及其水平如表1所示。

表1 试验因素及其水平表Tab.1 Test factors and their levels
2 计算模型
微流体惯性过滤器模型[2]如图1所示。图1中:a为管长;b为截面长度;θ为转折角;Vg为入口的气流速度。当气流进入过滤器之后,由于空气流场突然改变方向,在其中运动的颗粒的轨迹会与空气的流线发生一定的偏离。粒径较大的粒子由于惯性大,会撞击到壁面被收集;而粒径较小的粒子惯性小,会随着气流流出管外。

图1 微流体惯性过滤器模型Fig.1 Microfluidic inertial filter model
2.1 物理模型的简化假设条件
在本研究中:①设计的过滤器为扁型喷嘴入口,从而忽略了一个维度方向的速度,将流体的流动简化为二维的流动;②由于进入过滤器内的气流速度较小,远远小于当地声速,故将这种气体视为不可压缩气体处理;③在实际的工作条件下,不考虑气流的振荡对流场的影响,所以将气流流动视为定常流动;④颗粒撞击到壁面即认为收集,到达出口时即认为颗粒逃逸,不考虑二次夹带的影响。
由于本文主要对小雷诺数(Re<500)条件下的过滤器中运动的粒子进行研究,并且周光超,赵永凯,韩杰等[8]在亚微米粒子采样器的研究中采用颗粒轨道模型进行计算时,计算结果和试验结果十分一致,所以综合考虑以上简化条件。计算中对气相采用层流模型,对颗粒相采用颗粒轨道模型[9-10]。
2.2 计算条件
计算采用Fluent15.0商用软件,采用颗粒轨道模型对气相和颗粒相以及两相之间的相互耦合作用进行模拟。
①连续相。
进口条件:进口速度分别为Vg=2 m/s、4 m/s、6 m/s、8 m/s。出口条件:出口相对压力为Pout=0;壁面条件,静止、无速度滑移。
②离散相。
对射入的颗粒进行模拟时,将过滤器的入口设置为速度入口,给定的颗粒速度和气流速度相同,喷口类型为surface;出口设置为自由出口,并且将进出口条件均设置为逃逸面,壁面设置为吸收面[11-12]。
2.3 网格划分
本文创建二维几何模型并进行网格划分,整个计算区域采用非结构化网格,计算区域考虑边界层的影响。参考以往数值计算的经验和结果[4],为保证计算的准确性,单个过滤器通道内的网格数控制在(3~6)×104范围内。
3 结果及分析
正交试验设计及模拟计算结果如表2所示。

表2 正交试验方案设计及模拟计算结果Tab.2 Orthogonal test scheme and simulation calculation results
3.1 各因素对过滤器性能的影响
转折角、气流速度、截面长度和管长对过滤器的性能影响如图2~图5所示。由图2可知,随着转折角的增大,气流在通道内的偏折程度下降,颗粒受到的离心力减小,从而降低过滤效率;同时,转折处的局部压力损失减小,所以随着转折角的增大,压降呈现下降的趋势。图3表明,随着气流速度的增大,过滤效率有明显增大的趋势。经分析认为,气流速度越大,通过过滤器通道的气体速度越快,由于惯性力的作用,颗粒的跟随性变差,所以更容易撞击壁面而被收集;同时,气流速度的提高造成气流的沿程阻力损失增大,所以过滤器的压降呈增大的趋势。随着截面长度的增加,过滤器的过滤效率逐渐降低(见图4),这是由于截面长度的增加,颗粒在过滤器通道中的流通面积变大,同时气流的速度方向变化趋于平缓,从而使得颗粒对气流的跟随性较好,易于随着气流流出。图5显示,过滤效率和压降都没有显著的变化,说明管长对过滤器的性能影响不大。

图2 转折角对过滤器性能的影响Fig.2 Performance of filter under different

图3 气流速度对过滤器性能的影响Fig.3 Performance of filter under different Vg
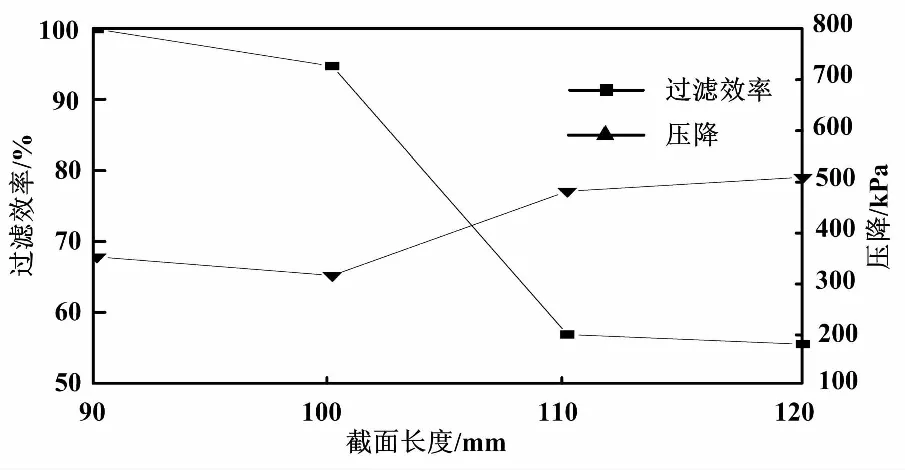
图4 截面长度对过滤器性能的影响Fig.4 Performance of filter under different b

图5 管长对过滤器性能的影响Fig.5 Performance of filter under different tube length
3.2 极差分析
运用极差分析法,分别对16组试验指标进行极差分析,并将极差分析的结果分别列于表3和表4中。由表3可知,在各因素对过滤效率的影响主次关系中,气流速度、截面长度和转折角对过滤效率的影响较大,是主要影响因素;而管长对过滤效率的影响较小,是次要因素。同理,由表4可知,气流速度和转折角对过滤效率的影响较大,是主要影响因素;而截面长度和管长对过滤效率的影响较小,是次要因素。
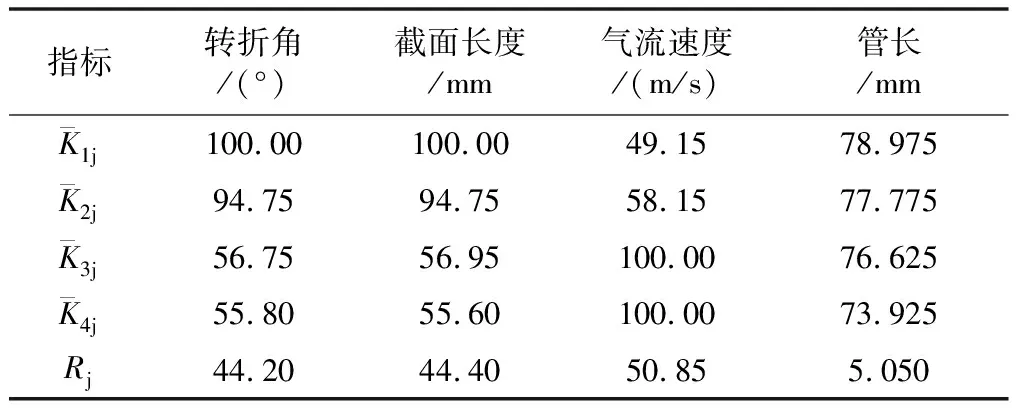
表3 各因素不同水平下的过滤效率平均值和极差Tab.3 Average value and range value of collection efficiency at different level

表4 各因素不同水平下的压降平均值和极差Tab.4 Average value and range value of pressure drop at different level
通过各因素不同水平下的滤效率平均值和压降平均值,选取各因素的平均过滤效率最高的水平组合方案1、平均压降最低的水平组合方案2、平均过滤效率中间值的水平组合方案3和平均压降中间值的水平组合方案4,得到过滤器的最优工艺参数组合如表5所示。
通过试验验证可见,计算分析所得的4种方案中,方案1的过滤效率最高,达到100%,但该过滤器的压降也最高,达到616 Pa;方案2的压降虽然最低,仅为32 Pa,但是过滤效率也低,基本上达不到过滤的目的;方案4的过滤效率最高为100%,但压降也较高,达到413 Pa。通过对比发现,方案3的过滤效率超过95%且压降较低,属于比较理想的参数组合,但是由于其过滤效率没有达到100%,可根据敏感性分析的结果,适当减小对压降影响不大的截面长度,可以得到最优的参数组合。

表5 计算分析所得最优工艺参数Tab.5 Optimal process parameters obtained from analyses
3.3 方差分析
运用方差分析法,得到的各因素过滤效率和压降的方差,分别如表6、表7所示。通常认为:当F>F0.01时,因素的影响特别显著;当F0.01>F>F0.05时,因素的影响显著;当F0.05>F>F0.1时,因素有一定影响;F 表6 各因素过滤效率方差Tab.6 Variance analysis of filtration efficiency of various factors 由表6可以看出,转折角、截面长度和气流速度对过滤效率的影响特别显著,管长对过滤效率的影响不大;由表7可以看出,气流速度对过滤器压降的影响显著,转折角对压降有一定的影响,而截面长度和管长对压降的影响不大。从上述分析可知,过滤效率和压降没有共同的主要影响因素,耦合度不高。其中,截面长度对过滤效率影响特别显著,但对压降影响不大。因此,为了提高过滤效率,可以适当减小截面长度。 表7 各因素压降方差Tab.7 Variance of pressure drop of various factors 本文利用Fluent计算软件对微流体惯性过滤器进行了数值模拟,得到了惯性过滤器的过滤效率和压降,并通过正交试验设计探究了各个因素对过滤性能的影响。结果表明,针对微流体惯性过滤器影响因素水平较多的情况,使用正交试验方法设计数值模拟的工况,科学地安排了模拟次数,精简了工作量。用少量具有代表性的试验研究了各个参数对过滤效率和压降的影响。此外,通过对试验结果的极差分析可知:转折角、截面长度和气流速度对过滤效率有特别显著的影响,而管长对过滤效率的影响不大;气流速度对压降的影响显著,转折角对压降有一定的影响,截面长度和管长对压降的影响不大。通过各因素对过滤器过滤性能的分析和极差分析可知,过滤效率和压降的变化是相互矛盾的,即减小压降会以减小一些效率为代价,但过滤效率和压降没有共同的主要影响因素,耦合度不高。因此,在优化设计中,可适当减小对过滤效率影响特别显著,但对压降影响不大的截面长度来提高过滤效率。

4 结束语
